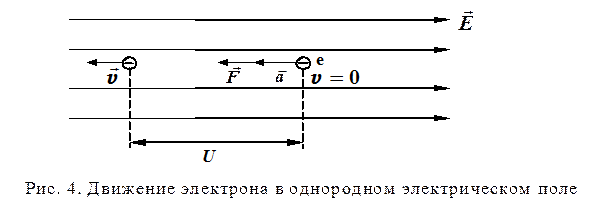В рамках физики и химии 100 лет как доказано, что материя состоит из электронов, протонов и нейтронов. Эксперименты демонстируют, что свободные нейтроны за 614 сек наполовину распадаются на электроны и протоны. Инерциальные свойства электронов протонов и нейтронов определяются методом масс — спектрометрии. Масс-спектрометр — прибор для определения масс заряженных частиц и массы атомов (молекул) по характеру движения их ионов в электрическом и магнитном полях.
Массу нейтрального атома нельзя измерить традиционной масс-спектрометрией. Однако, если отнять у него или добавить ему один и более электронов, то он превратится в йон, характер движения которого в этих полях будет определяться его массой и электрическим зарядом. Строго говоря, в масс-спектрометрах определяется не масса, а отношение массы к электрическому заряду. Если заряд известен, то однозначно определяется масса иона, а значит, можно вычислить массу нейтрального атома и его ядра. Конструктивно масс-спектрометры могут сильно отличаться друг от друга. В них могут использоваться как статичные поля, так и изменяющиеся во времени поля, магнитные и/или электрические.
Рассмотрим один из наиболее простых вариантов определения массы частицы.
Масс-спектрометр состоит из следующих основных частей:
Из ионного источника 1 ускоренные ионы через щель 2 попадают в область 3 постоянного и однородного электрического и магнитного полей. Направление электрического поля задаётся положением пластин конденсатора и показано стрелками. Магнитное поле направлено перпендикулярно плоскости рисунка.
В области 3 электрическое и магнитное поле отклоняют ионы в противоположные стороны и величины напряжённостей этих полей Е и Н1 подобраны так, чтобы силы их действия на ионы (соответственно qЕ и qvН1, где q — заряд, а v — скорость иона) компенсировали друг друга, т.е. было qЕ = qvН1. Создается монохроматичный пучок ионов. При скорости иона v = Е/Н1 он движется не отклоняясь в области 3 и проходит через вторую щель 4, попадая в область 5 однородного и постоянного магнитного поля напряжённостью Н2. В этом поле ион движется по окружности 6, радиус R которой определяется из соотношения mv 2 /R = qvH2, где m — масса иона. Так как v = Е/Н1, масса частицы определяется из соотношения
Таким образом, при известном заряде иона его масса определяется радиусом R круговой орбиты в области 5.
Схема масс-спектрометра:
- — ионный источник,
- — щелеваяе диафрагма,
- — область однородных и постоянных электрического и магнитного полей (силовые линии электрического поля направлены вдоль плоскости рисунка м показаны стрелками, область магнитного поля показана штриховкой, его силовые линии перпендикулярны плоскости рисунка),
- — щелевая диафрагма
- — область однородного и постоянного магнитного поля (силовые линии перпендикулярны плоскости рисунка),
- — траектория иона,
- — детектор.
Если в качестве детектора ионов (7) использовать фотопластинку, то этот радиус с высокой точностью покажет чёрную точку в том месте проявленной фотопластинки, куда попадал пучок ионов. В современных масс-спектрометрах в качестве детекторов обычно используют электронные умножители или микроканальные пластинки. Масс-спектрометр позволяет определять массы с очень высокой относительной точностью Δm/m = 10 -8 — 10 -7 .
Анализ масс-спектрометром смеси атомов различной массы позволяет также определить их относительное содержание в этой смеси. В частности, может быть установлено содержание различных изотопов какого-либо химического элемента.
Согласно принятой обработке эксперимента инерциальные силы полностью обусловлены инерциальными свойствами ньютоновской массы (m) — нейтральной, не несущей заряда материи. Однако, в эксперименте все анализируемые частицы несут заряды. Заряды, согласно электродинамике, обладают инерциальными свойствами без относительно к механической массе.
Cила Лоренца вызывает изменение магнитного поля, изменение которого, в свою очередь, вызывает появление ЭДС пропорциональной скорости изменения магнитного потока (ускорению).
εi= ∫ Ebdl = — — L dt
где dФ/dt -скорость изменения магнитного поля. Сопротивление изменению скорости и есть проявление инерции.
В тоже время при обработке результатов эксперимента инерциальные свойства, обусловленные наличием заряда, совершенно не учитываются. В 2012 году масс — спектроскопии исполнится 100 лет, но до настоящего времени не появилось ни одной работы, содержащей критические замечания, касающиеся обработки результатов эксперимента и, соответственно, ответов на следующий вопрос:
Почему не учитываются инерциальные свойства электрического заряда иона?
Соответственно, мы считаем необходимым предложить альтернативные варианты обработки экспериментальных данных, полученных в результате масс — спектроскопии микрочастиц.
Целью данной работы является изучение движения элементарных частиц в электрическом и магнитном полях, экспериментальное определение удельного заряда электрона с помощью магнетрона.
Электрон является носителем элементарного отрицательного заряда е (e = –1,6∙10 —19 Кл). Отношение его заряда к массе e/m называется удельным зарядом электрона. Удельный заряд может быть экспериментально определён различными методами. Все они основаны на поведении электрона в электрическом и магнитном полях.
В электрическом поле напряжённостью 
(рис .4) на электрон действует сила
, (2.9.1)
которая сообщает электрону ускорение 
и направлена против поля.
Под действием этой силы электрон, пройдя расстояние между точками с разностью потенциалов U, приобретает кинетическую энергию
. (2.9.2)
Движение электрона в однородном магнитном поле происходит под действием силы Лоренца
, (2.9.3)
где 
— вектор скорости электрона; 
— вектор индукции магнитного поля; е – заряд электрона.
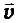
Сила Лоренца 
перпендикулярна как скорости электрона, так и направлению магнитного поля. Она не меняет модуля скорости и кинетической энергии частицы.
Модуль силы Лоренца
, (2.9.4)
где a — угол между векторами 
и .
Сила Лоренца сообщает электрону нормальное (центростремительное) ускорение и вызывает движение его по окружности радиуса R, если угол a составляет 90 o (рис. 5). Таким образом, по второму закону Ньютона:
, (2.9.5)
откуда радиус окружности
. (2.9.6)
Из формулы (2.9.6) видно, что радиус окружности зависит от удельного заряда e/m. Этот факт и положен в основу метода определения удельного заряда с помощью магнетрона.
Магнетрон представляет собой высоковакуумную электронную трубку, имеющую прямую металлическую нить (катод), расположенную по оси цилиндрического анода.
Для нашей работы магнетрон с успехом можно заменить обычной электронной лампой с цилиндрическим анодом, на оси которого расположен катод (рис. 6, а). Лампа помещается внутри длинного соленоида, при помощи которого параллельно оси создаётся магнитное поле напряжённостью .
Катод нагревается электрическим током и испускает электроны, которые под действием электрического поля движутся к аноду. Когда магнитное поле отсутствует, электроны движутся по радиу
сам цилиндрического анода (рис. 6 б, линия 1).
Если включить магнитное поле, траектория движения искривляется, и тем больше, чем сильнее поле (рис. 6, б, линия 2). Все электроны достигают анода, и величина анодного тока в цепи практически не изменяется до определённого момента, когда при дальнейшем увеличении магнитного поля радиус траектории всё больше уменьшается и при некотором критическом значении Вкр, электроны, не достигнув анода, вернутся обратно к катоду (рис. 6, б, линия 3).
При выполнении условия В > Вкр электроны уже не будут попадать на анод, и ток станет равен нулю (рис. 6, б, линия 4).
На рис. 7 приведен график зависимости анодного тока IА от индукции магнитного поля при некотором анодном напряжении UА (сбросовая характеристика магнетрона).
Если бы все электроны, вылетающие из катода, имели одну и ту же скорость, анодный ток IА спадал бы до нуля точно при критическом значении Вкр индукции магнитного поля (рис. 7, штриховая линия). Однако скорости вылетевших электронов разные, поэтому уменьшение тока происходит на довольно протяжённом участке вблизи Вкр (рис. 7, сплошная линия).
Критическое значение индукции магнитного поля является некоторой функцией анодного напряжения UА. Эту зависимость легко установить, если предположить, что скорость электрона при его движении в магнетроне остаётся постоянной по модулю. При В = Вкр, радиус окружности, по которой движется электрон, равен RА /2, где RА – радиус анода. Подставляя его в уравнение (2.9.6), получим:
. (2.9.7)
Решая совместно уравнения (2.9.2) и (2.9.7), получим формулу для расчёта удельного заряда электрона:
, (2.9.8)
где UА — разность потенциалов между катодом и анодом.
Индукция магнитного поля в соленоиде может быть рассчитана по закону Био — Савара — Лапласа или по теореме о циркуляции индукции магнитного поля по замкнутому контуру
, (2.9.9)
где 
– длина соленоида; N – число витков соленоида; Iсол — сила тока, протекающего через соленоид (сила намагничивающего тока); 
– магнитная постоянная.
Критическому значению индукции магнитного поля Вкр соответствует критическое значение силы тока Iкр. Учитывая это и подставляя (2.9.7) в (2.9.8), получим
. (2.9.10)
При выводе (2.9.10) предполагалось, что электрическое и магнитное поля действуют на электрон по очереди, сначала он в электрическом поле разгоняется до скорости 
, а затем с этой постоянной скоростью движется в магнитном поле.
В рассматриваемом случае электрон движется в скрещенных магнитном и электрическом полях и одновременно испытывает действие сил со стороны обоих полей. Вследствие этого, скорость электрона не постоянна (она возрастает по мере приближения к аноду), а траектория его движения отличается от круговой. Данное обстоятельство позволяет утверждать, что формула (2.9.10) не точна. Тем не менее, как следует из результатов точного анализа рассматриваемой задачи, эта формула в целом удовлетворительно описывает физику процессов и с точностью до коэффициента пропорциональности является правильной.
Окончательная расчётная формула имеет вид:
, (2.9.11)
где = 0,1 м; N = 1000 витков; RА = 5 мм; A – коэффициент, учитывающий отличие реальной траектории движения электрона в скрещенных электрическом и магнитном полях от окружности. Для нашей экспериментальной установки А=1,3.
Тщательные измерения удельного заряда и известное из опытов Милликена (1909 г.) значение величины заряда электрона позволили определить его массу и установить зависимость массы от скорости.
В принципе теми же методами определяются массы атомов и молекул. Соответствующие приборы для определения масс атомов и молекул (точнее, их ионов) носят название масс-спектрографов. Для примера можно рассмотреть принципиальное устройство одного из масс-спектрографов (рис. 8).
Сначала пучок ионов проходит через фильтр скоростей, в котором на движущиеся ионы одновременно действуют взаимно перпендикулярные электрическое и магнитное поля. Направления полей выбираются так, чтобы силы, действующие на ионы с их стороны, были противоположны по направлению. Через щель фильтра, противоположную входной, выходят только те ионы, на которые действуют равные по величине силы 
и 
.
q∙E = q∙ ∙B. (2.9.12)
Следовательно, из фильтра вылетают ионы одинаковых скоростей
. (2.9.13)
При выходе из фильтра частицы попадают в магнитное поле, перпендикулярное их скорости. Траектория их движения — окружность, радиус которой зависит от удельного заряда частицы
. (2.9.14)
Попадая на фотопластинку, ионы оставляют след, расстояние которого от выходной щели фильтра зависит от удельного заряда ионов.
По найденным значениям q/m можно определить массы ионов.
В наши дни точность определения масс ионов с помощью масс-спектрографов достигают 6 —8 значащих цифр (правда, не в граммах, а по отношению к массе эталонного атома).
Масс-спектрографические методы позволяют проводить количественный анализ нефти, состоящий из молекул различных углеводородов, трудно различимых обычными химическими способами. При большой мощности ионного пучка этот метод позволяет разделять изотопы в заметных количествах.
Масс-спектрографический метод часто применяют для определения изотопного состава исследуемого вещества. В частности, он был применён при исследовании лунного грунта. Близость изотопного состава земных и лунных пород свидетельствует об одновозрастности и единстве происхождения земного и лунного вещества. По-видимому, это следует распространить и на другие космические тела солнечной системы. Исследования вещества метеоритов не противоречат такому обобщению.
Масс-спектрографы нашли широкое применение в различных областях физики, химии, техники. Они используются для определения содержания примесей в газах, для анализа состава и процентного содержания различных смесей углеводородов и т. д.
Необходимые приборы: лабораторный стенд, внутри которого смонтированы все элементы схемы; цифровой вольтметр (или осциллограф).
На рис. 9 приведена схема экспериментальной установки, которая технически реализована на лабораторном стенде с возможностью самостоятельно вручную и с управлением от внешних источников изменять параметры эксперимента.
Экспериментальная установка состоит из трёх цепей.
Цепь намагничивающей катушки состоит из соленоида, создающего однородное магнитное поле при подключении к нему источника постоянного тока ε3, регулятора тока с внутренним и внешним управлением (коммутация осуществляется тумблером S1) и низкоомного резистора R5 =1 Ом, предназначенного для контроля силы тока Iсол в соленоиде по величине напряжения на этом сопротивлении.
Анодная цепь состоит из электронной лампы Л, источника постоянного тока ε1, делителя напряжения на резисторах R2, R3, R4 и последовательно включенного резистора R1 = 1кОм, предназначенного для контроля силы тока в анодной цепи IА, по величине напряжения на этом резисторе.
Цепь накала включает в себя нитевидный катод К лампы Л, источник тока ε2 и тумблер S2 , отключающий его.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10070 — 
| 7511 — 
или читать все.
Учащимся
Каким же образом можно экспериментально определить массу электрона или протона, ускоряя заряженную частицу на известном отрезке пути в известном однородном электрическом поле и измеряя ее конечную скорость? Как известно, если тело проходит путь d в направлении силы F, то работа Fd, затраченная на перемещение тела, равна приращению его кинетической энергии. Если же движение начинается от состояния покоя, то эта работа равна также конечной кинетической энергии тела: Fd= mv 2 /2
Таким образом, если известны F, d и v, то отсюда можно найти массу m.
В опытах, о которых пойдет речь, интересующие нас заряженные частицы ускоряются однородным силовым полем между двумя заряженными металлическими пластинами. Зная расстояние между пластинами и число заряжающих их батарей, можно определить электрическую силу, приложенную к каждому элементарному заряду. Опыты производятся в вакууме, чтобы исключить сопротивление воздуха, имевшее место в микро-микровесах. Кроме того, поскольку протоны и электроны более чем в 10 11 раз легче пластмассовых шариков, использованных в микро-микровесах, в данных опытах можно пренебречь силой тяготения по сравнению с электрическими силами.
Некоторое количество водорода подвергается ионизации вблизи пары заряженных пластин (рис.), после чего некоторые из ионов заходят с пренебрежимо малой скоростью через небольшое отверстие в пространство между пластинами. По мере движения ионов от одной пластины к другой электрическое поле ускоряет ионы, сообщая им конечную кинетическую энергию mv 2 /2. В правой пластине имеется небольшое отверстие, через которое некоторые из ионов могут попадать в камеру длиной 0,50 м (рис.). Эта камера изготовлена из проводящего материала, и, поскольку в ней нет электрического поля, ионы проходят всю ее длину без изменения своей скорости. На прохождение всего этого пути иону требуется всего лишь несколько микросекунд (1 мкс=10 -6 с). Хотя этот промежуток времени и очень мал, все же он доступен точному измерению посредством специального измерительного устройства. Это позволяет точно определить конечную скорость иона v.
Для измерения времени прохождения ионами длинной камеры от одного конца до другого надо заметить момент, когда данный ион покинет данную точку слева, и время, когда этот же ион достигнет дальнего конца справа. Чтобы заметить время, когда данный ион входит в длинную камеру, помещаем около входа пару небольших отклоняющих пластин (рис.). С их помощью можно управлять направлением пучка водородных ионов. Когда отклоняющие пластины заряжены, на ионы водорода действует боковая электрическая сила, которая отклоняет их в сторону от их траектории. Если же затем разрядить отклоняющие пластины, то по продольной оси камеры будут двигаться только те ионы, которые только что или позже попали в камеру; поэтому первыми ионами, прошедшими отверстие на дальнем конце, будут те, которые прошли весь путь в 0,50 м за время с момента разрядки пластин. Приход этих ионов регистрируется воспринимающим элементом, помещенным за отверстием.
Для измерения промежутка времени с момента разрядки пластин до момента прихода первых ионов на воспринимающий элемент отклоняющие пластины в камере соединяются с вертикальными отклоняющими пластинами осциллографа (рис.). Момент разряжения пластин в длинной камере отмечается пиком на кривой, вычерчиваемой на экране, осциллографа. Воспринимающий элемент у дальнего конца длинной камеры присоединяется к тем же вертикальным отклоняющим пластинам осциллографа (электрические соединения обоих концов камеры выполняются совершенно одинаково). Когда пучок ионов попадает в воспринимающий элемент, на экране осциллографа появляется второй пик (рис.). Два пика появляются в разных местах экрана, так как они возникли в разное время. В течение промежуточного времени между этими двумя моментами развертывающая цепь осциллографа вызывает горизонтальное перемещение электронного пучка на экране. Электронный пучок в осциллографе проходит расстояние между двумя пиками за то же время, за какое ионы водорода проходят 0,50 м в камере.
В современных осциллографах цепь развертки может вызвать горизонтальное перемещение электронного пучка на экране трубки от одного конца до другого за несколько сотых долей микросекунды. Для измерения скорости ионов цепь развертки настраивается так, чтобы вся кривая проходилась за 5 микросекунд. Тогда два пика на экране осциллографа будут заметно разделены. Измерением расстояния между пиками определяется время, за которое пучок пересекает длинную камеру. Находят промежуток времени от момента, когда пучок получает возможность двигаться прямо вперед, до момента, когда он попадает в воспринимающий элемент, с точностью до 0,01 микросекунды. В случае ионов водорода и 90- вольтовой батареи, создающей ускоряющую электрическую силу, время пролета равно 3,82 микросекунды. Отсюда можно вычислить скорость v ионов в длинной камере. Она равна 0,50 м/(3,82*10 -6 с) = = 1,31*10 5 м/с.
С другой стороны, пластины здесь ровно втрое дальше друг от друга, чем в микро-микровесах, в которых производился опыт Милликена,; кроме того, здесь используется втрое меньше таких же батарей. Поскольку сила, приходящаяся на элементарный заряд, пропорциональна числу одинаковых батарей и обратно пропорциональна расстоянию между пластинами, на каждый элементарный заряд теперь должна действовать в девять раз меньшая сила, т. е. 1/9*10 -14 ).
Если предположить, что один атом водорода несет один элементарный заряд, то каждый ион между пластинами испытывает только что выраженную силу. Двигаясь от одной пластины к другой, ион проходит путь 9,3 10 -3 м по направлению силы, так что произведенная работа по перемещению иона равна Fd = 1/9(1,4*10 -14 Н)*( 9,3 10 -3 м)= 1,4 10 -17 Дж. Следовательно,
mv/2=m (1,3*10 5 м/с) 2 /2=1,4 *10 -17 Дж.
Отсюда для массы иона водорода т находим
m= 1,7 *10 -27 кг.
Но ведь эта величина нам хорошо известна. В пределах точности наших измерений она совпадает с массой атома водорода.
Теперь можно подвести итог. Если ион водорода заряжен однократно, то его масса почти равна массе атома водорода. Можно даже сделать дальнейший шаг и утверждать, что ион водорода действительно является носителем единичного заряда и что его масса практически равна массе атома. Это должно быть правильным, так как предположение, что ион несет больший заряд, приведет к абсурдному результату. Например, если ион несет два элементарных заряда, то действительная величина mv 2 /2 должна быть в два раза больше принятого нами значения. Поскольку мы измеряли v, это может только значить, что масса иона в два раза больше найденной нами. Такой ион водорода обладал бы массой, в два раза превосходящей массу атома, осколком которого он является. Этот вывод настолько неправдоподобен, что мы его отбрасываем.
Ранее уже имелись указания, что электроны представляют собой строительные элементы, входящие во все атомы. По-видимому, ион водорода представляет собой атом водорода, потерявший один электрон. Кроме того, мы никогда ни в этом, ни в других опытах не встречали положительно заряженного осколка водорода с двумя положительными элементарными зарядами. Это одно из многих доказательств того, что положительно заряженный ион водорода является конечным строительным элементом. Это — протон. Когда водород расщепляется на заряженные частицы, то, как только что было установлено, протону принадлежит почти вся масса атома. Поэтому электроны должны быть очень легкими. Можно использовать те же приборы для измерения массы электрона и таким образом проверить этот вывод.
Рассчитайте массу (в а.е. м. с точностью до целых чисел) и заряд (в элементарных зарядах) ядер атомов следующих элементов:
4
9
B
e
,
6
12
C
,
3
6
L
i
. Сколько электронов содержится в атоме каждого из этих химических элементов?
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Радиоактивность. Строение атомного ядра. Энергия связи. Ядерные реакции. Номер №2046
Решение
4
9
B
e
. Масса 9 а.е.м. Заряд 4 элементарных зарядов.
6
12
C
. Масса 12 а.е.м. Заряд 6 элементарных зарядов.
3
6
L
i
. Масса 6 а.е.м. Заряд 3 элементарных заряда.
Если атом находится в нейтральном состоянии, то количество электронов в нём равно количеству протонов. Таким образом,
4
9
B
e
содержит 4 электрона.
6
12
C
содержит 6 электронов.
3
6
L
i
содержит 3 электрона.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 июля 2020 года; проверки требуют 3 правки.
Элемента́рный электри́ческий заря́д — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц. Согласно изменениям определений основных единиц СИ равен точно 1,602 176 634⋅10−19 Кл[1] в Международной системе единиц (СИ)[2]. Тесно связан с постоянной тонкой структуры, описывающей электромагнитное взаимодействие[3].
Квантование электрического заряда[править | править код]
Любой наблюдаемый в эксперименте электрический заряд всегда кратен одному элементарному — такое предположение было высказано Б. Франклином в 1752 году и в дальнейшем неоднократно проверялось экспериментально. Впервые элементарный заряд был экспериментально измерен Милликеном в 1910 году[3].
Тот факт, что электрический заряд встречается в природе лишь в виде целого числа элементарных зарядов, можно назвать квантованием электрического заряда. При этом в классической электродинамике вопрос о причинах квантования заряда не обсуждается, поскольку заряд является внешним параметром, а не динамической переменной. Удовлетворительного объяснения, почему заряд обязан квантоваться, пока не найдено, однако уже получен ряд интересных наблюдений.
- Если в природе существует магнитный монополь, то, согласно квантовой механике, его магнитный заряд обязан находиться в определённом соотношении с электрическим зарядом любой выбранной элементарной частицы. Отсюда автоматически следует, что существование всего одного магнитного монополя влечёт за собой квантование всех электрических зарядов во Вселенной. Однако обнаружить в природе магнитный монополь не удалось.
- В современной физике элементарных частиц разрабатываются модели наподобие преонной, в которых все известные фундаментальные частицы оказывались бы простыми комбинациями новых, ещё более фундаментальных частиц. В этом случае квантование заряда наблюдаемых частиц не представляется удивительным, поскольку оно возникает «по построению».
- Не исключено также, что все параметры наблюдающихся частиц будут описаны в рамках единой теории поля, подходы к которой разрабатываются в настоящее время. В таких теориях величина электрического заряда частиц должна вычисляться из крайне небольшого числа фундаментальных параметров, возможно, связанных со структурой пространства-времени на сверхмалых расстояниях. Если такая теория будет построена, тогда то, что мы наблюдаем как элементарный электрический заряд, окажется некоторым дискретным инвариантом пространства-времени (скажем, топологическим). Такой подход развивается, например, в модели С. Бильсона-Томпсона[4], в которой фермионы Стандартной модели интерпретируются, как три ленты пространства-времени, заплетённые в косу (брэд), а электрический заряд (точнее, треть от него) соответствует перекрученной на 180° ленте. Однако несмотря на изящество таких моделей, конкретных общепринятых результатов в этом направлении пока не получено.
Дробный электрический заряд[править | править код]
С открытием кварков стало понятно, что элементарные частицы могут обладать дробным электрическим зарядом, например, ±⅓ и ±⅔ элементарного. Однако подобные частицы существуют только в связанных состояниях (конфайнмент), таким образом, почти все известные свободные частицы (и все стабильные и долгоживущие) имеют электрический заряд, кратный элементарному, хотя рассеяние на частицах с дробным зарядом наблюдалось.
Исключением является t-кварк, его время жизни (~5·10⁻²⁵ с) настолько мало́, что он распадается раньше, чем успевает подвергнуться адронизации, и поэтому встречается только в свободном виде. Заряд t-кварка по прямым измерениям равен +⅔𝑒[5].
Неоднократные поиски долгоживущих свободных объектов с дробным электрическим зарядом, проводимые различными методиками в течение длительного времени, не дали результата.
Стоит, однако, отметить, что электрический заряд квазичастиц также может быть не кратен целому. В частности, именно квазичастицы с дробным электрическим зарядом отвечают за дробный квантовый эффект Холла.
Экспериментальное определение элементарного электрического заряда[править | править код]
Число Авогадро и постоянная Фарадея[править | править код]
Если известны число Авогадро 𝑁A и постоянная Фарадея 𝐹, величину элементарного электрического заряда можно вычислить, используя формулу
(другими словами, заряд одного моля электронов, делённый на число электронов в моле, равен заряду одного электрона.)
По сравнению с другими, более точными методами, этот метод не даёт высокой точности, но всё-таки точность его достаточно высока.
Ниже приводятся подробности этого метода.
Значение постоянной Авогадро 𝑁A было впервые приблизительно измерено Иоганном Йозефом Лошмидтом, который в 1865 году определил на газокинетической основе размер молекул воздуха, что эквивалентно расчету числа частиц в заданном объёме газа[6]. Сегодня значение 𝑁A может быть определено с очень высокой точностью с использованием очень чистых кристаллов (как правило — кристаллов кремния) путём измерения расстояния между атомами с использованием дифракции рентгеновских лучей; или другим способом, с точным измерением плотности кристалла. Отсюда можно найти массу (𝑚) одного атома, а так как молярная масса (𝑀) известна, число атомов в моле может быть рассчитано так: 𝑁A = 𝑀/𝑚.
Величина 𝐹 может быть измерена непосредственно с помощью законов электролиза Фарадея. Законы электролиза Фарадея определяют количественные соотношения, основанные на электрохимических исследованиях, опубликованных Майклом Фарадеем в 1834 году[7]. В эксперименте электролиза существует взаимно-однозначное соответствие между количеством электронов проходящих между анодом и катодом, и количеством ионов, осевших на пластине электрода. Измеряя изменения массы анода и катода, а также общий заряд, проходящий через электролит (который может быть измерен как интеграл по времени от электрического тока), а также учитывая молярную массу ионов, можно вывести 𝐹.
Ограничения на точность метода заключается в измерении 𝐹. Лучшие экспериментальное значения имеют относительную погрешность 1,6 промилле, что примерно в тридцать раз больше, чем в других современных методах измерения и расчета элементарного заряда.
Опыт Милликена[править | править код]
Известный опыт по измерению заряда электрона e. Маленькая капля масла в электрическом поле будет двигаться с такой скоростью, что будут скомпенсированы сила тяжести, сила Стокса (производная от вязкости воздуха) и электрическая сила. Сила тяжести и Стокса могут быть рассчитаны исходя из размера и скорости падения капли в отсутствие электрического поля, откуда может быть определена и электрическая сила, действующая на каплю. Поскольку электрическая сила, в свою очередь, пропорциональна произведению электрического заряда и известной, заданной в эксперименте, напряжённости электрического поля, электрический заряд капли масла может быть точно вычислен. В этих опытах измеренные заряды различных капель масла оказались всегда целыми кратными одной небольшой величины, а именно e.
Дробовой шум[править | править код]
Любой электрический ток сопровождается электронным шумом от различных источников, одним из которых является дробовой шум. Существование дробового шума связано с тем, что ток является не непрерывным, а состоит из дискретных электронов, которые поочерёдно поступают на электрод. Путём тщательного анализа шума тока может быть вычислен заряд электрона. Этот метод, впервые предложенный Вальтером Шоттки, может давать значение е с точностью до нескольких процентов[8]. Тем не менее, он был использован в первом прямом наблюдении Лафлином квазичастиц, причастных к дробному квантовому эффекту Холла[9].
Эффект Джозефсона и константа фон Клитцинга[править | править код]
Другим точным методом измерения элементарного заряда является вычисление его из наблюдения двух эффектов квантовой механики: эффекта Джозефсона, при котором возникают колебания напряжения в определённой сверхпроводящей структуре и квантового эффекта Холла, эффекта квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Постоянная Джозефсона
где h — постоянная Планка, может быть измерена непосредственно с помощью эффекта Джозефсона.
Постоянная фон Клитцинга
может быть измерена непосредственно с помощью квантового эффекта Холла.
Из этих двух констант может быть вычислена величина элементарного заряда:
Примечания[править | править код]
- ↑ Elementary charge (англ.). The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. Дата обращения: 20 мая 2020.
- ↑ В системе СГСЭ элементарный заряд равен точно 4,803 204 712 570 263 72⋅10−10 Фр. Значение в единицах СГСЭ приведено как результат пересчёта значения CODATA в кулонах с учётом того факта, что кулон точно равен 2 997 924 580 единицам электрического заряда СГСЭ (франклинам или статкулонам).
- ↑ 1 2 Томилин К. А. Фундаментальные физические постоянные в историческом и методологическом аспектах. — М.: Физматлит, 2006. — С. 96—105. — 368 с. — 400 экз. — ISBN 5-9221-0728-3.
- ↑ A topological model of composite preons (недоступная ссылка) es.arXiv.org
- ↑
Abazov V. M. et al. (DØ Collaboration). Experimental discrimination between charge 2𝑒/3 top quark and charge 4𝑒/3 exotic quark production scenarios (англ.) // Physical Review Letters : journal. — 2007. — Vol. 98, no. 4. — P. 041801. — doi:10.1103/PhysRevLett.98.041801. — Bibcode: 2007PhRvL..98d1801A. — arXiv:hep-ex/0608044. — PMID 17358756. - ↑ Loschmidt J. Zur Grösse der Luftmoleküle (нем.) // Sitzungsberichte der kaiserlichen Akademie der Wissenschaften Wien. — 1865. — Bd. 52, Nr. 2. — S. 395—413. English translation Архивировано 7 февраля 2006 года..
- ↑ Ehl R. G., Ihde A. Faraday’s Electrochemical Laws and the Determination of Equivalent Weights (англ.) // Journal of Chemical Education (англ.) (рус. : journal. — 1954. — Vol. 31, no. May. — P. 226—232. — doi:10.1021/ed031p226. — Bibcode: 1954JChEd..31..226E.
- ↑ Beenakker C., Schönenberger C. Quantum Shot Noise (англ.) // Physics Today. — 2003. — May (vol. 56, no. 5). — P. 37—42. — doi:10.1063/1.1583532. — arXiv:cond-mat/0605025. [исправить]
- ↑ de-Picciotto R. et al. Direct observation of a fractional charge (англ.) // Nature. — 1997. — Vol. 389, no. 162—164. — P. 162. — doi:10.1038/38241. — Bibcode: 1997Natur.389..162D..
Электрон — это стабильная отрицательно заряженная элементарная частица.
Электроны играют важную роль почти во всех физических эффектах. Поскольку электроны несут заряд, они также генерируют электрическое поле. Если привести электрон в движение, то возникнет магнитное поле. Если электрон проходит через другое внешнее электрическое поле, его путь изменяется под действием силы Лоренца.
Электрон принадлежит к лептонному семейству частиц. Существует несколько различных семейств частиц, перечисленных в стандартной модели физики частиц.
Спин электрона и магнитный момент электрона.
Согласно современному уровню знаний, лептоны являются элементарными частицами. По сравнению с другими лептонами, электрон имеет самую низкую массу среди лептонов, несущих заряд. Он принадлежит к первому поколению лептонов. Второе и третье поколения — мюон и тауон. Эти две частицы имеют одинаковые с электроном заряды и спин, но отличаются от него большей массой.
Лептоны отличаются от других фундаментальных частиц, таких как кварки, отсутствием сильного взаимодействия. Все лептоны принадлежат к семейству фермионов, поэтому электрон имеет собственный вращательный момент ( спин ) s = ½ в единицах ℏ, где ℏ — приведённая постоянная Планка).
« Как и любая заряженная частица со спином, электрон обладает магнитным моментом, причём магнитный момент делится на нормальную часть и аномальный магнитный момент (добавка примерно 0,116 %). Магнитный момент электрона μe = -9,2847647043(28)⋅10−24 Дж/Тл. »
Википедия
Атомы и молекулы.
Электроны связаны с ядрами атомов «притягивающей» кулоновской силой. Такой состав из атомного ядра и одного или нескольких электронов называется атомом. Электроны движутся вокруг ядра атома. Если число электронов отличается от заряда ядра, то это ион.
Волновая природа связанных электронов описывается атомными орбиталями. Каждая из этих орбиталей имеет ряд квантовых чисел, таких как энергия и момент. Кроме того, у атома может быть только дискретное число орбиталей. В силу принципа Паули на орбитали может находиться максимум два электрона, спин которых имеет разные знаки.
Химическая связь между атомами возникает благодаря электромагнитным взаимодействиям, которые описываются с помощью квантовой физики. Самые прочные связи создаются путем обмена или передачи электронов. Это позволяет образовывать молекулы. В молекулах электроны движутся аналогично атомам и занимают молекулярные орбитали. Однако фундаментальным отличием является образование пар электронов с разными спинами. Это позволяет нескольким электронам занимать одну орбиталь без нарушения принципа Паули.
Делимость электрического заряда
Хорошо известно, что молекулы и атомы в их нормальном состоянии не имеют электрического заряда. Поэтому мы не можем объяснить электризацию их движением. Однако если мы предположим, что частицы с электрическим зарядом существуют в природе, то мы должны обнаружить, что существует предел деления электрического заряда.
Согласно различным экспериментам, проведенным советским ученым Абрамом Федоровичем Иоффе и американским ученым Робертом Милликеном, было обнаружено, что существует заряженная частица с минимальным зарядом, который невозможно разделить.
В своих экспериментах они электризовали маленькие частицы цинковой пыли. Заряд пылинок меняли и вычисляли. Это было проделано несколько раз. При этом заряд оказывался каждый раз другим. Однако все изменения были кратны целому числу, большему, чем некоторый минимальный заряд (т.е. 2, 3, 4 и т.д.). Этот результат можно интерпретировать только следующим образом. Только наименьший заряд (или целое число таких зарядов) присоединяется к пылинке цинка или отсоединяется от нее. Этот заряд дальше уже не делится. Частица с наименьшим зарядом называется электроном.
Также в ходе опытов было установлено, что любая частица вещества либо электрически нейтральна, либо имеет заряд, кратный по модулю заряду электрона.
Свойства электрона
Электрон характеризуется и другими важными свойствами, помимо спина и магнитного момента. Рассмотрим их.
Масса электрона
Электроны очень малы. Масса электрона составляет me = 9,109 • 10-31 кг или 5, 489 • 10-4 атомных единиц массы (а. е. м). Эта масса примерно в 3700 раз меньше массы молекулы водорода, которая является самой маленькой из всех молекул. Из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт).
Отношение массы протона к массе электрона равно 1836, то есть протон в 1836 раз «тяжелее» электрона.
Заряд электрона
Электрический заряд — одно из основных свойств электрона. Невозможно представить, что с электронов можно снять заряд. Они неотделимы друг от друга.
Электрический заряд — это физическая величина. Она обозначается буквой q. Единицей электрического заряда является кулон (Кл). Эта единица названа в честь французского физика Шарля Кулона. Электрон — это частица с наименьшим отрицательным зарядом. Его заряд равен e0 = — 1,6 • 10-19 Кл.
Модуль заряда электрона назвали элементарным электрическим зарядом. Его обозначают е. Измерения показали, что e = 1,6 • 1019 Кл.
Обратите внимание, что любой, даже самый малый, заряд тела содержит целое число элементарных зарядов. Так как заряд тела обозначается буквой q, то получаем: q = eN, где N — целое число (N = 1, 2, 3, … ).
Элементарный заряд может показаться очень малым, однако вспомним: в любом теле, видимом невооружённым глазом, содержится невообразимо большое число заряженных частиц. Так, суммарный заряд электронов в одной столовой ложке воды равен по модулю примерно миллиону кулонов (а вы уже знаете, как велик заряд всего в 1 Кл).
Важно! Термин элементарный заряд был придуман, когда предположили, что этот заряд является наименьшим электрическим зарядом в природе. Сегодня мы знаем, что 1/3 элементарного заряда также приходится на кварки.
Энергия покоя электрона
Энергия электрона рассчитывается из эквивалентности массы и энергии. Вы знаете это как формулу из теории относительности E=mc2. E означает энергию, m — массу, а c — скорость света. Как было уже сказано выше в этой статье: «из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт)».
В формуле это можно рассчитать следующим образом: E = mec2 = 9,109 • 10-31 • (3 • 108 )2 = 8,2 • 10-14 Дж = 0,511 • 106 эВ ≈ 0,511 МэВ
Список литературы
Список литературы
- Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
- Бронштейн М. П. Атомы и электроны. — М.: Наука. — 1980. — 152 с., Библиотечка «Квант», вып. 1. Тир. 150000 экз.
Упражнение 46 № 1, Параграф § 53 из решебника ГДЗ на белый учебник по Физике 9 класса от авторов А. В. Пёрышкин, Е. М. Гутник. Готовое домашнее задание актуально на 2014-2018 годы.
Условие
Определите массу (в а. е. м. с точностью до целых чисел) и заряд (в элементарных зарядах) ядер атомов следующих химических элементов: углерода ; лития ; кальция .
Другие задания из этого решебника
