
Диаграмма
состояния системы, где компоненты
образуют одно химическое соединение
АmBn
представлена на рисунке. Точка С
соответствует составу химического
соединения АmBn
постоянного состава. Избыток любого из
компонентов (А или В) понижает температуру
плавления соединения. Именно поэтому
температура его плавления является
наиболее высокой, что отражает наличие
максимума на линии ликвидус. Если сделать
разрез по линии С- АmBn,
то диаграмму можно рассматривать как
сочетание двух диаграмм первого типа
для систем А- АmBn
и АmBn-В,
в которых полностью отсутствует
растворимость в твердом состоянии.
Поскольку
химическое соединение АmBn
обладает собственной температурой
плавления, то кривая охлаждения для
сплава, проходящего непосредственно
по ординате химического соединения
абсолютно аналогична кривой охлаждения
для чистого компонента.
Соединения,
в которых отношение между количествами
компонентов выражается целыми числами,
называются стехиометрическими или
дальтонидами, так как они удовлетворяют
закону кратных отношений, открытому
Дальтоном.
Из
данного рисунка видно, что химическое
соединение, образованное компонентами
А и В, может содержать их в отношениях
несколько отличающихся от соответствующих
AmBn,
т.е. на диаграмме имеется более или менее
обширная область существования однородной
фазы на основе этого соединения,
ограниченная кривыми ab,
bC, Cd
и de – так называемая
область гомогенности.

Слева от вертикальной
штриховой линии в химическом соединении
имеется дефицит атомов В, а справа –
атомов А. Такие соединения были названы
бертоллидами в честь французского
химика Бертолле. Можно так же сказать,
что эти соединения нестехиометрические.
Следует отметить, что кривая охлаждения
для сплава, проходящего через точку С
будет иметь точно такой же вид как и
кривая для стехиометрического химического
соединения AmBn.
§3.6. Пятый вид диаграмм. Компоненты а и в образуют непрочное соединение, разлагающееся ниже температуры плавления.
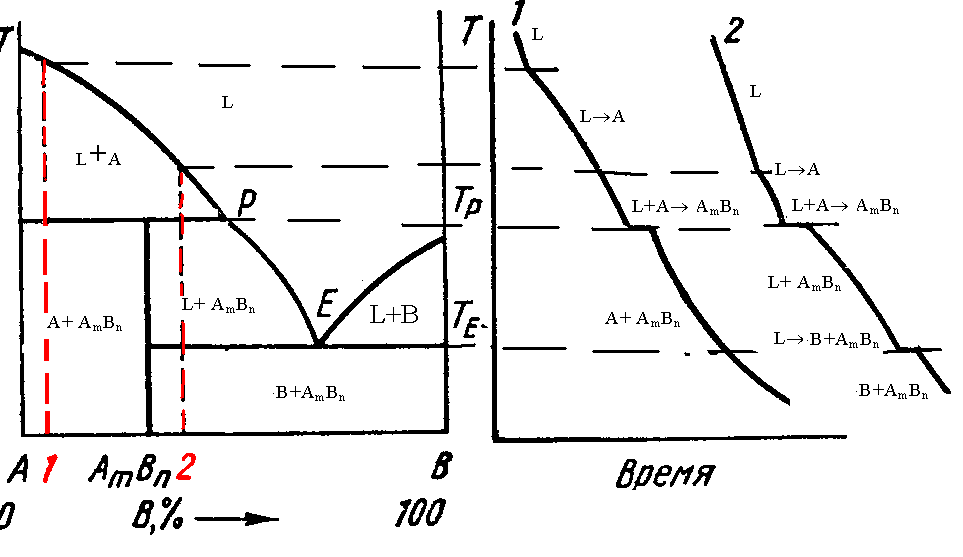
Из-за
неустойчивости химического соединения
оно не может выделяться при температурах
выше Тр. При температурах ниже
Тр оно образуется по перитектической
реакции L+A
AmBn.
Так же как в случае устойчивого химического
соединения, неустойчивое соединение
может быть стехиометрическим и
нестехиометрическим.
§3.7. Пример.

-
Для
каждой области диаграммы назовите
присутствующие фазы. -
Определите
концентрации (в атомных процентах)
каждого компонента в сосуществующих
фазах для системы, содержащей 20 ат.% V
при температуре 1230С. -
Нарисуйте
кривые охлаждения и опишите процессы,
происходящие при охлаждении систем,
содержащих 5 и 60 ат.% V. -
Рассчитайте
массу каждой фазы и массу каждого
компонента в каждой фазе для системы,
содержащей 20 ат.% V при
температуре 1000С,
если общая масса системы 100 грамм. -
Рассчитайте
сколько грамм и какого компонента в
минимальном количестве необходимо
добавить в систему, содержащую 10 ат.%
Zr при температуре 1600С,
чтобы она из двухфазной превратилась
в однофазную при той же температуре,
если масса всей системы равна 200 грамм. -
Определите
число термодинамических степеней
свободы в точках, указанных на диаграмме.
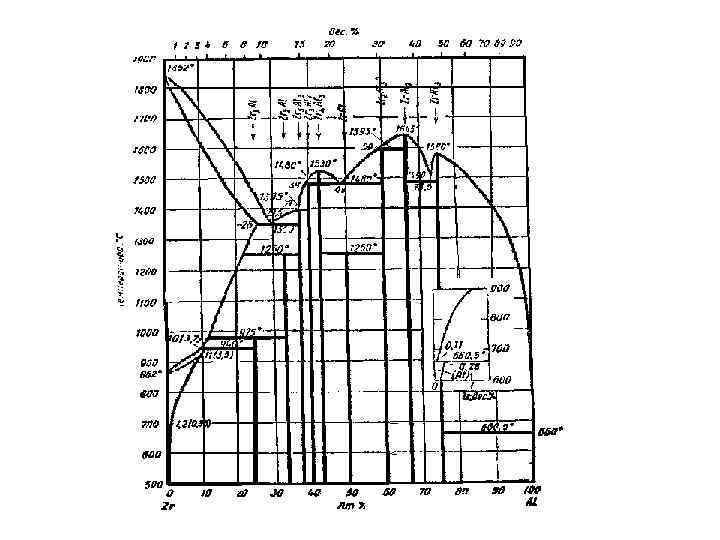
Перед Вами реальная
диаграмма Zr-V.
Разберем последовательно все пункты
задания.
Но прежде следует
обратить внимание на то, что данная
диаграмма имеет две шкалы. Построена
диаграмма в атомных процентах и на
нижней шкале отложены атомные проценты,
а необходимая для выполнения некоторых
заданий шкала весовых процентов нанесена
сверху. Она неравномерна, в отличие от
равномерной шкалы атомных процентов.
-
Для
каждой области диаграммы назовите
присутствующие фазы.
В этом пункте кроме
определения, какие фазы существуют в
той или иной области хорошо бы определить
типы реакций, протекающих на горизонталях,
типы химических соединений, если таковые
имеются, растворимость компонентов
друг в друге в твердом состоянии, если
таковая имеется.
Расстановку фаз
начинают с того, что находят все
однофазные области, которые есть на
диаграмме. Как видно из вышеизложенного
вариантов всего три. Это область, в
которой существует расплав (L),
всегда находящаяся выше линии ликвидус;
области твердых растворов на основе
компонентов и нестехиометрические
химические соединения. На данной
диаграмме таких однофазных областей
всего три.
Область I,
область жидкого расплава – ее мы
обозначили L.
Область II
– область твердого раствора на основе
циркония или твердый раствор ванадия
в цирконии. Растворимость твердого V
в твердом Zr составляет
16,5 ат.% V или 10 вес.% V.
Эти проценты обычно наносят на диаграмму
и здесь они нанесены под точкой а,
это крайняя левая точка горизонтали
при температуре 1230С.
Область III
– область твердого раствора на основе
ванадия или твердый раствор циркония
в ванадии. Максимальная растворимость
циркония в ванадии определяется точкой
n, это крайняя правая
точка горизонтали при 1300С.
Нестехиометрических
химических соединений в этом случае
нет, зато есть одно стехиометрическое
ZrV2. Поскольку оно
не имеет точки плавления, а образуется
по перитектической реакции – неустойчивое
химическое соединение. Его состав 67
ат.%V и 33 ат.% Zr.
Зная состав химического соединения в
атомных процентах, легко определить
формулу химического соединения, если
она неизвестна. Делают это так:
![]()
.
Таким образом, на 1 атом Zr
приходится 2 атома V,
следовательно, имеем формулу ZrV2.
Теперь определяем,
какие фазы сосуществуют в двухфазных
областях. Для того чтобы это определить,
достаточно посмотреть, что ограничивает
двухфазную область справа и слева. Это
могут быть либо однофазные области,
либо ординаты чистых компонентов и
химических соединений.
Область IV
слева ограничена однофазной областью
, справа однофазной
областью L. Имеем: +
L.
Область V
аналогична IV, только
справа она ограничена однофазной
областью . В области
V – +L.
Область VI
слева ограничена однофазной областью
L, справа ординатой
химического соединения ZrV2.
В области L+ ZrV2.
Область VII
– слева – однофазная область, справа
– ордината ZrV2. В
области + ZrV2.
Область VIII
– слева – ордината чистого Zr,
справа – . В области
+ Zr.
Область IX
– слева – ордината ZrV2,
справа – . В области
+ ZrV2.
Область X
– ограничена двумя ординатами. Слева
– чистого Zr, справа – ZrV2.
В области
механическая смесь твердых
кристаллов Zr + ZrV2.
Далее определим,
какие реакции протекают на горизонталях,
присутствующих на диаграмме. Это полезно
сделать, потому что при выполнении
остальных заданий может понадобиться,
как, например, при построении кривых
охлаждения.
Всего существует
4 типа реакций: эвтектическая, эвтектоидная,
перитектическая, перитектоидная. С
перитектоидной реакцией в нашем курсе
Вы не встретитесь. С эвтектической и
перитектической встречались при
рассмотрении простых диаграмм. Довольно
часто попадается и эвтектоидная.
Как отличить, где
протекает та или иная реакция на
диаграмме?
Эвтектическая и
эвтектоидная реакции протекают на
горизонталях, над которыми линии ликвидус
или солидус образуют воронку.
В
результате и эвтектической, и эвтектоидной
реакций получается механическая смесь
двух твердых фаз. Это могут быть твердые
растворы, химические соединения, чистые
компоненты. Только по эвтектической
реакции эта смесь получается из жидкости,
а по эвтектоидной из твердого раствора.
Lтвердое1+твердое2
– эвтектическая. твердое1+твердое2
– эвтектоидная.
П
еритектическая
реакция, в основном, появляется в случае
образования неустойчивого химического
соединения (и стехиометрического и
нестехиометрического). По виду напоминает
букву Т (в случае стехиометрического
соединения) или букву Т с толстой ножкой
(в случае нестехиометрического). В
области, находящейся над перитектической
горизонталью всегда присутствует жидкий
расплав (L) и твердое
вещество (может быть: твердый раствор,
чистый компонент или другое химическое
соединение). По перитектической реакции
из смеси расплава и твердого получается
химическое соединение.
L+твердоеAmBn
(или ).
На диаграмме Zr-V
присутствуют все три типа реакций.
При температуре
1300С – перитектическая
+LZrV2.
При температуре
1230С – эвтектическая
L+
ZrV2.
При температуре
777С – эвтектоидная
Zr+
ZrV2.
-
Определите
концентрации (в атомных процентах)
каждого компонента в сосуществующих
фазах для системы, содержащей 20 ат.% V
при температуре 1230С.
Определить
концентрации компонентов в сосуществующих
фазах – это значит определить сколько
атомных процентов каждого из компонентов
содержится в той или иной фазе.
Данная нам точка
попадает на эвтектическую горизонталь.
Поскольку здесь протекает реакция L+
ZrV2, то мы должны
определить состав трех сосуществующих
фаз (L,
и ZrV2).
Состав -фазы
определяется точкой а. Здесь 16,5 ат.%
V и 83,5 ат.% Zr.
Состав жидкости
определяется точкой Е. В ней 43,5 ат.% V
и 56,5 ат.% Zr.
Состав ZrV2
определяется точкой d.
Мы уже определяли этот состав: 67 ат.% V
и 33 ат.% Zr.
Если взять тот же
процент ванадия, но попросить определить
состав сосуществующих фаз, например,
при1400С, то мы будем
определять состав уже двух фаз, тех
которые существуют в этой области: L
и .
Для того, чтобы определить состав
необходимо провести коноду через
заданную точку (см. диаграмму). Состав
-фазы
будет определяться точкой, лежащей на
линии солидус (f), состав
жидкости – точкой, лежащей на линии
ликвидус (m). Состав -фазы:
12 ат.% V и 88 ат.% Zr.
Состав жидкости: 34 ат.% V
и 66 ат.% Zr.
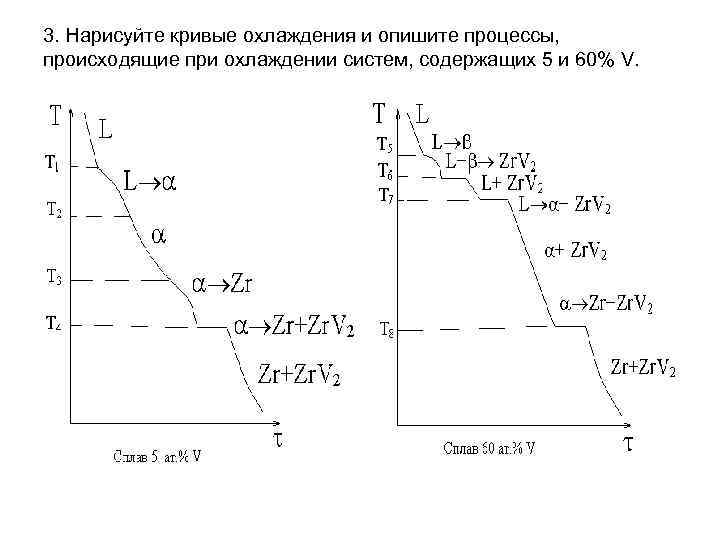
3. Нарисуйте
кривые охлаждения и опишите процессы,
происходящие при охлаждении систем,
содержащих 5 и 60 ат.% V.
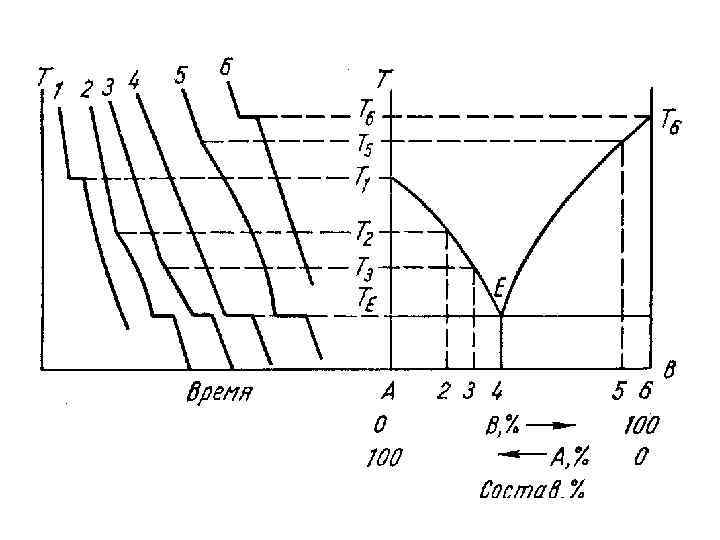
На рисунке
представлены кривые охлаждения. Для
того чтобы описать процессы, происходящие
при охлаждении сплавов, достаточно
написать на самой кривой какие процессы
протекают и какие фазы охлаждаются.

Кривая для сплава,
содержащего 5 ат.% V. До
температуры Т1 охлаждается
жидкость. В этой точке начинается
выделение твердых кристаллов
(на кривой наблюдается излом), которое
продолжается до температуры Т2,
здесь исчезают последние капли жидкости
(заканчивается излом) и далее до
температуры Т3 происходит охлаждение
твердой -фазы. В
точке 3 из -фазы
выделяются кристаллы Zr
(наблюдается второй излом) до температуры
Т4. Точка 4 находится на горизонтали
нонвариантного эвтектоидного превращения
(Zr+
ZrV2), на кривой
охлаждения наблюдается площадка. Ниже
температуры Т4 охлаждается
механическая смесь кристаллов Zr
и ZrV2.
Кривая для сплава,
содержащего 60 ат.% V строится
аналогично. Ордината этого сплава
пересекает все три горизонтали,
присутствующие на этой диаграмме.
Следовательно, на кривой охлаждения
будет три площадки.
4. Рассчитайте
массу каждой фазы и массу каждого
компонента в каждой фазе для системы,
содержащей 20 ат.% V
при температуре 1000С,
если общая масса системы 100 грамм.
Найдя эту точку,
попадаем в область, в которой сосуществуют
две фазы
и ZrV2. Найдем их массы
по правилу рычага. Напоминаем, что решать
задачу с помощью правила рычага можно
только, выражая состав фаз в весовых
процентах.
Проведем через
данную точку коноду и определим весовой
процент ванадия и циркония в каждой
точке.

По правилу рычага
![]()
![]()
гр.
![]()
![]()
гр.
Можно себя проверить.
В сумме массы двух фаз должны давать
массу сплава (в нашем случае 100 гр.).
Действительно, 90,9+9,1=100 гр.
Теперь рассчитаем
массы каждого компонента в каждой фазе.
1. Масса ванадия
в -фазе.
Содержание ванадия в -фазе
составляет 8 вес.%, следовательно, если
умножить массу фазы на весовую долю
компонента в этой фазе, мы найдем массу
компонента в данной фазе.
![]()
гр.
2. Масса циркония
в -фазе.
Содержание циркония в -фазе
92 вес.%.
![]()
гр.
3. Масса ванадия в
ZrV2. Содержание
ванадия в этой фазе – 52 вес.%.
![]()
гр.
4. Масса циркония
в ZrV2. Содержание
циркония в этой фазе – 48 вес.%.
![]()
гр.
Тоже можно себя
проверить. Сложив массы двух компонентов,
получим массу фазы, в которой искали
их. Сложив массы всех четырех компонентов
найдем массу сплава.
5. Рассчитайте
сколько грамм и какого компонента в
минимальном количестве необходимо
добавить в систему, содержащую 10 ат.% Zr
при температуре 1600С,
чтобы она из двухфазной превратилась
в однофазную при той же температуре,
если масса всей системы равна 200 грамм.
Находим эту точку.
Следует обратить внимание, что здесь
задание дано не в процентах ванадия, а
в процентах циркония. 10 ат.% Zr
– это 90 ат.% V. Таким образом
мы попадем в область, обозначенную на
диаграмме цифрой V. Также
как в предыдущей задаче, проведем коноду
и определим весовые проценты в
каждой точке.

В средней точке
мы имеем две фазы. Если мы переместимся
вправо, то попадем в однофазную область
, и будем добавлять
V. Если будем перемещаться
влево, то попадем в жидкость, и будем
добавлять Zr. В задаче
сказано «в минимальном количестве»,
это означает, что достаточно посчитать,
сколько компонента надо добавить, чтобы
перейти на линию ликвидус или солидус,
или ординату химического соединения.
Исходный сплав
содержит 83 г V
в 100 г раствора (по определению весового
процента). Но у нас 200 г раствора, значит
и ванадия в нем будет в два раза больше
– 166 г. Если мы добавляем X
грамм V
к 166 г V,
содержащемся в растворе, то и вся масса
раствора увеличивается на X
г. Добавив такое количество V,
получаем новый сплав, содержащий 94 г V
в 100 г раствора.
Все эти рассуждения
можно записать в виде простой пропорции:
166+X
200+X
94
100
Решаем
пропорцию:
(166+X).100=94.(200+X)
6X=2200
X=366,7
г ванадия
Аналогично
рассуждаем в случае добавления Zr.
Исходный сплав
содержит 17 г Zr
в 100 г раствора или 34 г в 200 г раствора.
Если мы добавляем Y
грамм Zr
к 34 г Zr,
содержащемся в растворе, то и вся масса
раствора увеличивается на Y
г. Добавив такое количество V,
получаем новый сплав, содержащий 38 г Zr
в 100 г раствора.
34+Y
200+Y
38
100
Решив уравнение,
получаем, что добавить надо 67,7 г циркония.
Итак, чтобы система
превратилась из двухфазной в однофазную
при постоянной температуре надо добавить
или 366,7 г ванадия, или 67,7 г циркония.
6. Определите
число термодинамических степеней
свободы в точках, указанных на диаграмме.
Число компонентов
на двухкомпонентной диаграмме может
быть только два или один.
Один компонент
– в случае если точка принадлежит
ординате чистого компонента или ординате
химического соединения (в этом случае
само химическое соединение считается
компонентом), в том числе и воображаемой
ординате нестехиометрического химического
соединения.
Число фаз –
может быть одна, две или три.
Одна фаза –
однофазные области; ординаты чистых
компонентов и химических соединений,
исключая точки плавления и фазовых
превращений.
Две фазы –
двухфазные области; точки плавления и
точки фазовых переходов чистых компонентов
и химических соединений.
Три фазы –
любая горизонталь, где протекает
эвтектическое, эвтектоидное, перитектическое
или перитектоидное превращения.
При определении
количества фаз действует правило:
вертикаль главнее горизонтали, т.е. в
месте пересечения вертикали и горизонтали
– точка принадлежит горизонтали.
Рассчитаем числа
степеней свободы в точках, указанных
на диаграмме.
Точка 1. К=1 (Zr),
Ф=2 (Zr-твердый, Zr-жидкий),
С=1-2+1=0.
Точка 2. К=1 (Zr),
Ф=2 (Это точка фазового перехода, т.е. до
этой температуры кристаллизуется одна
модификация твердого циркония, допустим
-Zr, а
в этой точке он превращается, скажем, в
-Zr.
Поэтому фаз две), С=1-2+1=0.
Точка 3. К=1 (Zr),
Ф=1 (Zr-твердый), С=1-1+1=1.
Точка 4. К=2 (Zr,
V), Ф=2 (L, ),
С=2-2+1=1.
Точка 5. К=2 (Zr,
V), Ф=3 (L, ,
ZrV2), С=2-3+1=0.
Точка 6. К=2 (Zr,
V), Ф=3 (Zr, ,
ZrV2), С=2-3+1=0.
Точка 7. К=1 (ZrV2),
Ф=1 (ZrV2 – твердый),
С=1-1+1=1.
Точка 8. К=2 (Zr,
V), Ф=3 (L, ,
ZrV2. Хотя эта точка
и лежит на пересечении вертикали и
горизонтали, но она принадлежит
горизонтали, т.к. сначала должно произойти
перитектическое превращение, в результате
которого образуется химическое
соединение), С=2-3+1=0.
Точка 9. К=2 (Zr,
V), Ф=2 (,
ZrV2), С=2-2+1=1.
Точка 10. К=2 (Zr,
V), Ф=1 (),
С=2-1+1=2.
Точка 11. К=2 (Zr,
V), Ф=1 (L),
С=2-1+1=2.
Определить массу жидкой и твердой фаз
Знаток
(270),
на голосовании
2 года назад
Голосование за лучший ответ
Дина Марковская
Мыслитель
(6416)
2 года назад
В исходной смеси было х моль алюминия и х моль кремния.
27х+28х = 1000
х = 18.18 моль
Масса алюминия в смеси: 18.18*27 = 491 г = 0.491 кг
Масса кремния в смеси 0.509 кг. Значит, массовая доля кремния в исходном сплаве: 50.9%.
Вы попадаете в двухфазную область. Проведя ноду, видим, что здесь твердый кремний и жидкий расплав, в котором примерно 28-29 процентов кремния по массе (72-71 процента алюминия).
Алюминия у нас было 0.491 кг, сейчас эти 0.491 кг есть в жидкой фазе и составляют 72% от ее массы.
Масса жидкой фазы 0.491/0.72 = 0.694 кг
Остальное составляет твердая фаза, твердый кремний, 1 – 0.682 = 0.318 кг
A.S.Dostankyzy*Знаток (270)
2 года назад
При 298 К в гальваническом элементе протекает следующая реакция:
2MnO4- +5Pb2+ + 2H2O = 2Mn2+ + 5PbO2 + 4H+
Температурный коэффициент элемента равен dE0/ dT =210-4 В/град, а стандартные электродные потенциалы равны следующим значениям:
0(MnO4-/ Mn2+) = +1,51 В; 0(PbO2/Pb2+) = +1,68 B.
Рассчитайте G, S и H реакции при 298 К. (4 балл)
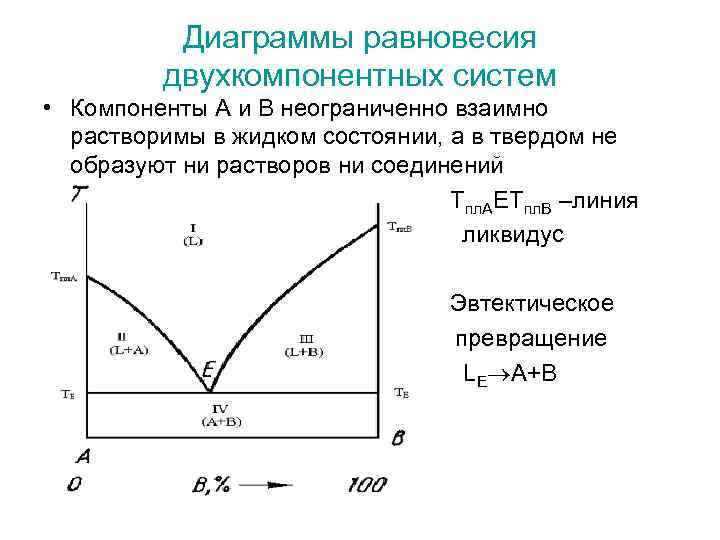
Диаграммы равновесия двухкомпонентных систем • Компоненты А и В неограниченно взаимно растворимы в жидком состоянии, а в твердом не образуют ни растворов ни соединений Тпл. АЕТпл. В –линия ликвидус Эвтектическое превращение LE A+B
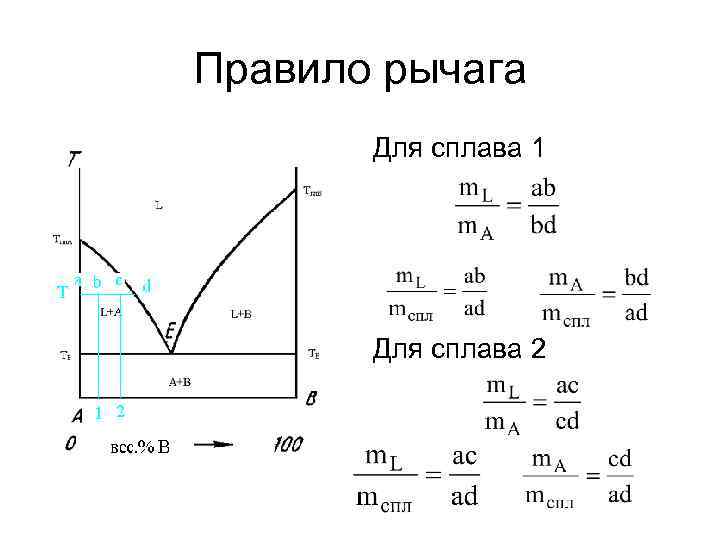
Правило рычага Для сплава 1 Для сплава 2
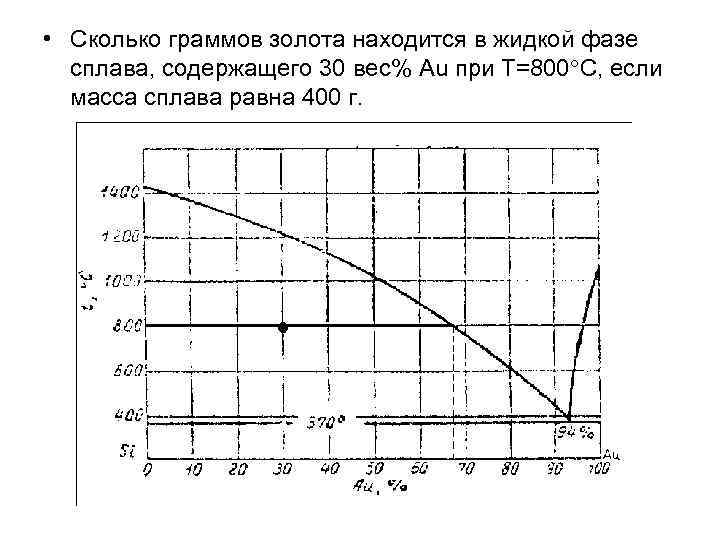
• Сколько граммов золота находится в жидкой фазе сплава, содержащего 30 вес% Au при Т=800 С, если масса сплава равна 400 г.
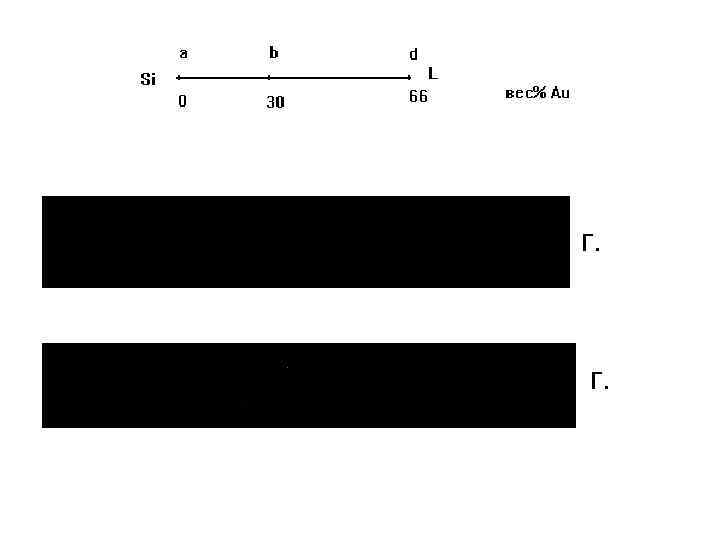
г.
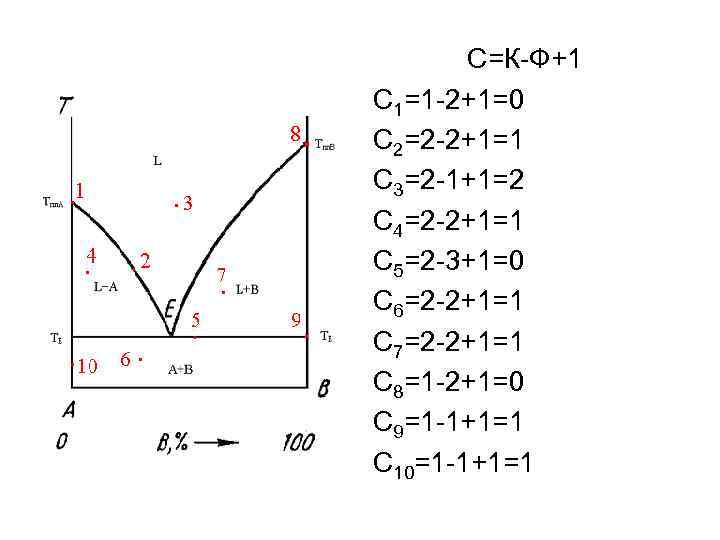
С=К-Ф+1 С 1=1 -2+1=0 С 2=2 -2+1=1 С 3=2 -1+1=2 С 4=2 -2+1=1 С 5=2 -3+1=0 С 6=2 -2+1=1 С 7=2 -2+1=1 С 8=1 -2+1=0 С 9=1 -1+1=1 С 10=1 -1+1=1
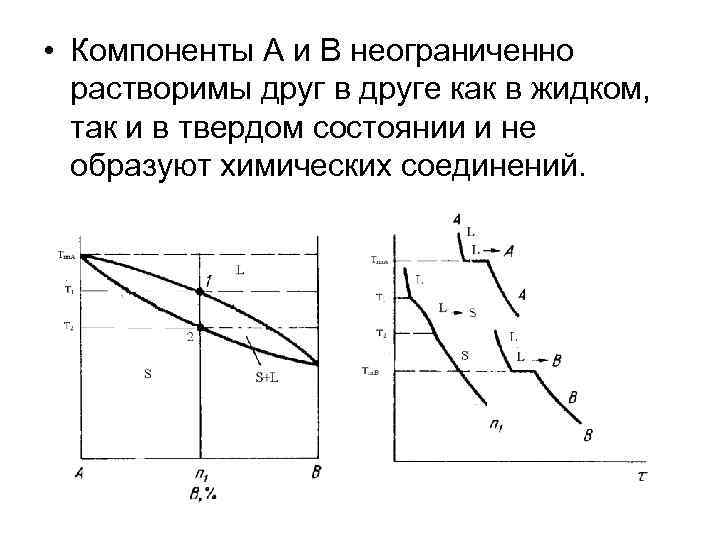
• Компоненты А и В неограниченно растворимы друг в друге как в жидком, так и в твердом состоянии и не образуют химических соединений.
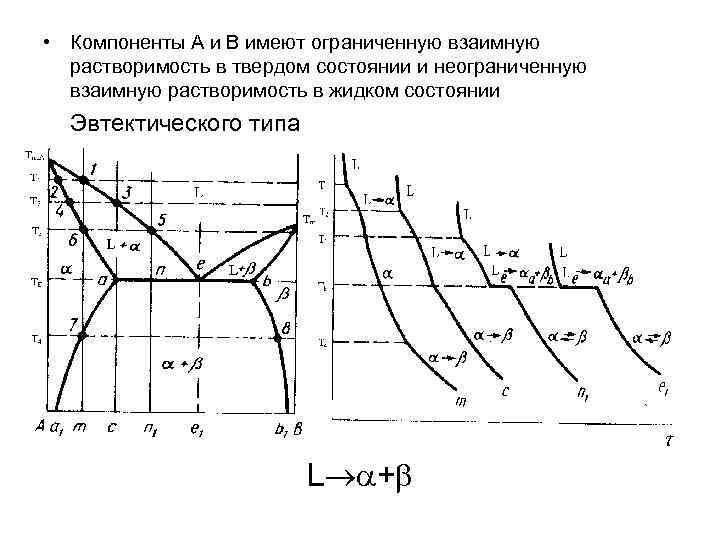
• Компоненты А и В имеют ограниченную взаимную растворимость в твердом состоянии и неограниченную взаимную растворимость в жидком состоянии Эвтектического типа L +
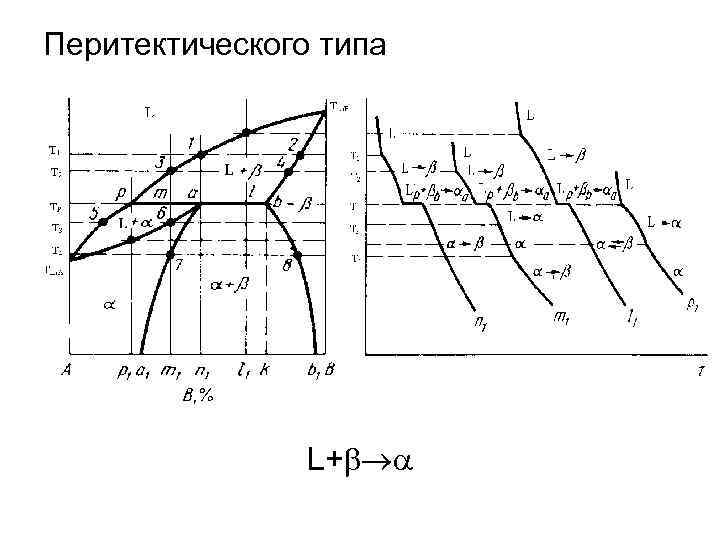
Перитектического типа L+
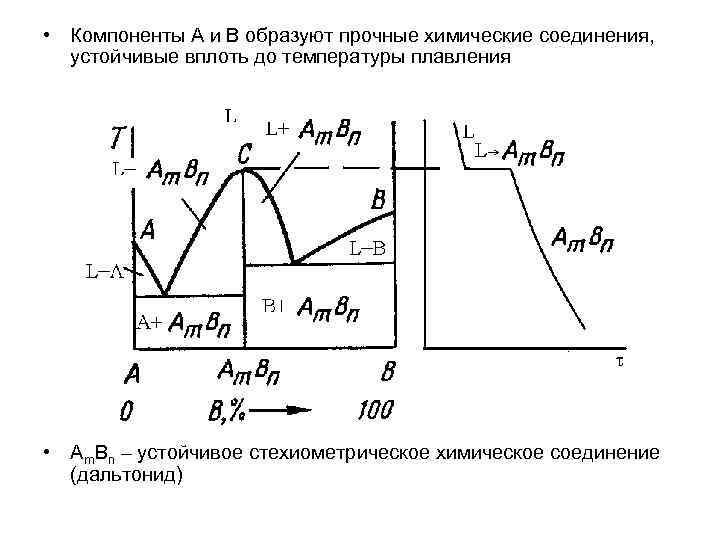
• Компоненты А и В образуют прочные химические соединения, устойчивые вплоть до температуры плавления • Аm. Bn – устойчивое стехиометрическое химическое соединение (дальтонид)
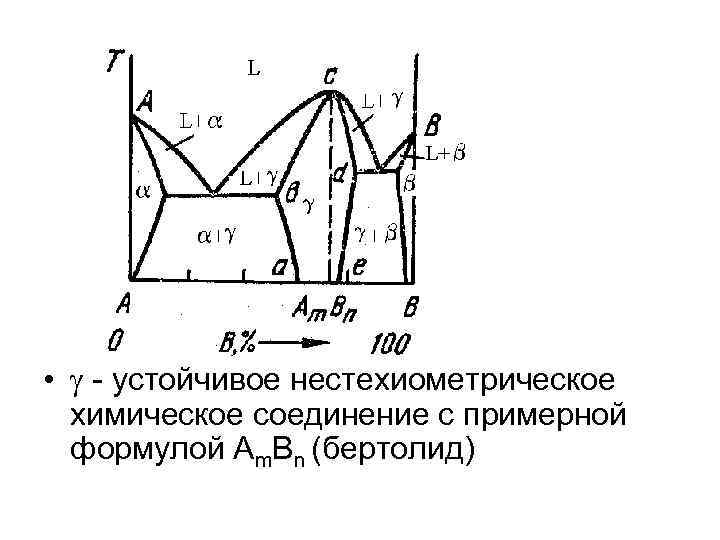
• – устойчивое нестехиометрическое химическое соединение с примерной формулой Аm. Bn (бертолид)
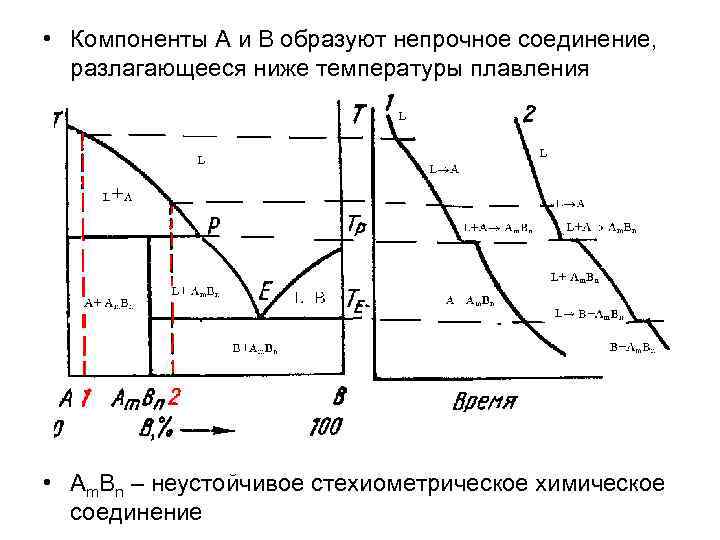
• Компоненты А и В образуют непрочное соединение, разлагающееся ниже температуры плавления • Аm. Bn – неустойчивое стехиометрическое химическое соединение
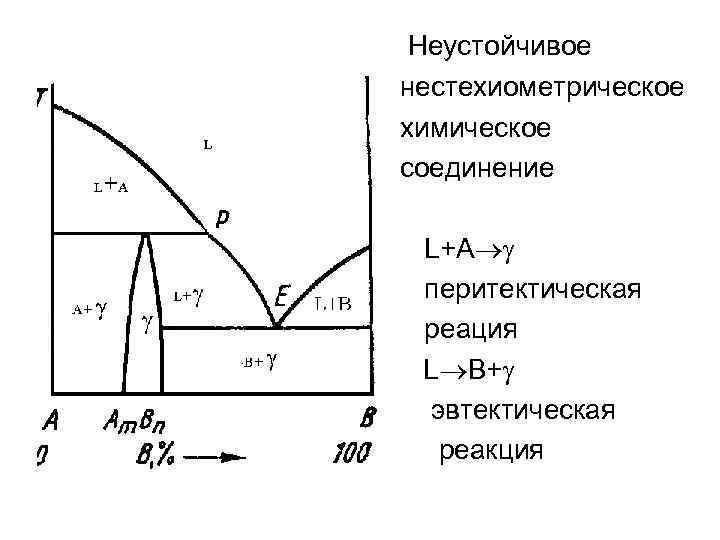
Неустойчивое нестехиометрическое химическое соединение L+A перитектическая реация L B+ эвтектическая реакция

• L тв 1 + тв 2 Эвтектическая р-ция • тв 1 + тв 2 Эвтектоидная р-ция L+тв Аm. Bn или Перитектическая р-ция тв 1+тв 2 Аm. Bn или Перитектоидная р-ция

• Число компонентов (K) 1 – на любой ординате (чистого компонента или химического соединения) 2 – на всей остальной диаграмме

• Число фаз (Ф) 1 – однофазные области ординаты чистых компонентов и химических соединений исключая Тпл, Тполим. превр. , Тразл. неуст. х. с. 2 – двухфазные области Тпл, Тполим. Превр 3 – любая горизонталь, исключая крайние точки
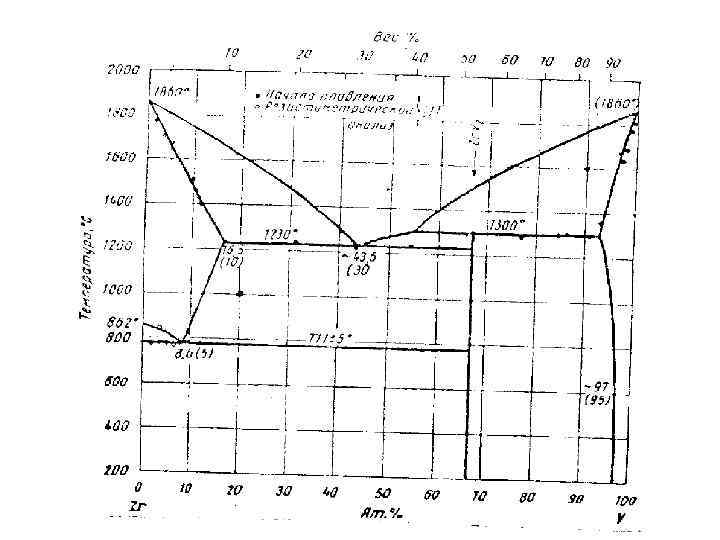
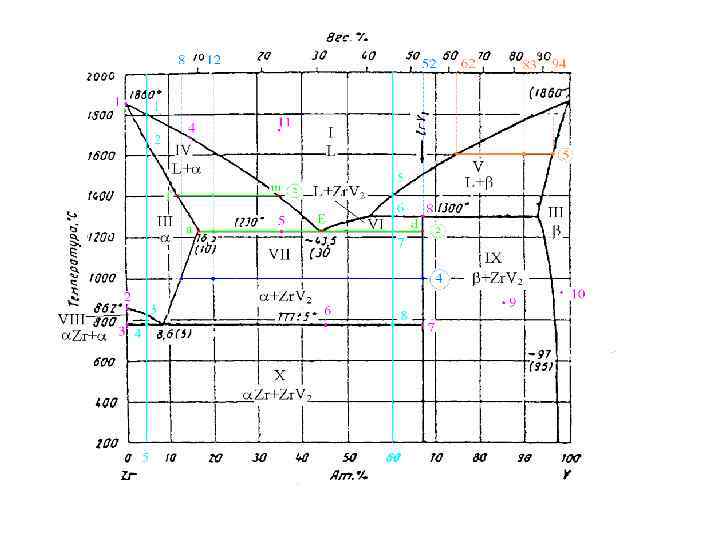

2. Определите концентрации (в атомных процентах) каждого компонента в сосуществующих фазах для системы, содержащей 20 ат. % V при температурах 1800, 1400, 1230, 1000, 777 и 400 С. Т=1500 С L: 20 ат% V; 80 ат% Zr T=1400 С L: 35 ат% V; 65 ат% Zr : 11 ат% V; 89 ат% Zr T=1230 С L: 43, 5 ат% V; 56, 5 ат% Zr : 16, 5 ат% V; 83, 5 ат% Zr Zr. V 2: 67 ат% V; 33 ат% Zr T=1000 С : 12 ат% V; 88 ат% Zr Zr. V 2: 67 ат% V; 33 ат% Zr T=777 С -Zr: 0 ат% V; 100 ат% Zr : 8, 6 ат% V; 91, 4 ат% Zr Zr. V 2: 67 ат% V; 33 ат% Zr T=400 С -Zr: 0 ат% V; 100 ат% Zr Zr. V 2: 67 ат% V; 33 ат% Zr
3. Нарисуйте кривые охлаждения и опишите процессы, происходящие при охлаждении систем, содержащих 5 и 60% V.
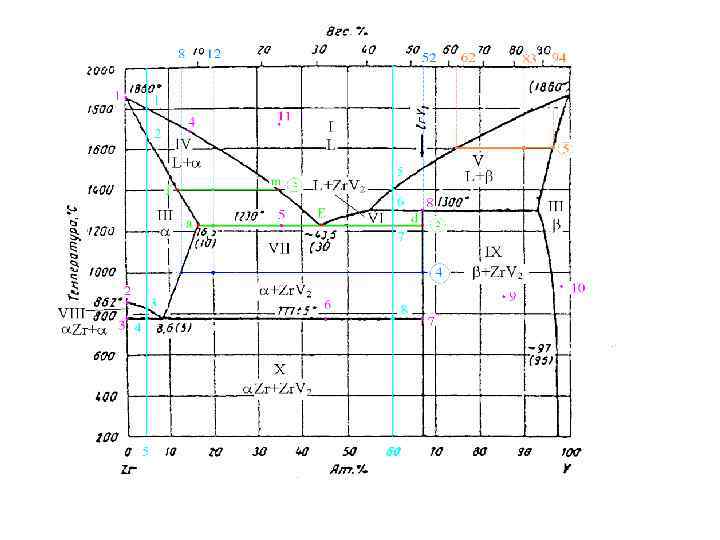

4. Рассчитайте массу каждой фазы и массу каждого компонента в каждой фазе для системы, содержащей 20 ат. % V при температуре 1000 С, если общая масса системы 100 грамм. гр.

гр.
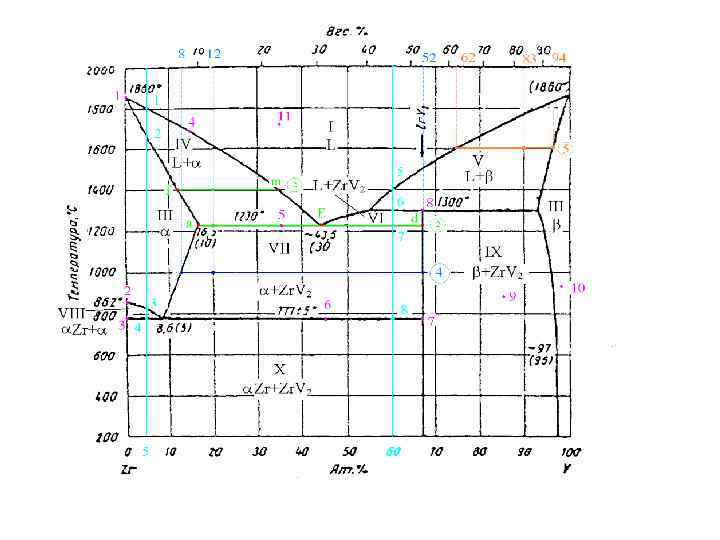

5. Рассчитайте сколько грамм и какого компонента в минимальном количестве необходимо добавить в систему, содержащую 10 ат. % Zr при температуре 1600 С, чтобы она из двухфазной превратилась в однофазную при той же температуре, если масса всей системы равна 200 г.

• Добавляем V 83 гр. V в 100 гр. раствора 166 гр. V в 200 гр. раствора 166+Х – 200+Х 94 100 (166+Х). 100= (200+Х). 94 16600+100 Х=18800+94 Х 6 Х=2200 Х=366, 7 гр.

• Добавляем Zr 17 гр. Zr в 100 гр. раствора 34 гр. Zr в 200 гр. раствора 34+Y – 200+Y 38 100 (34+Y). 100= (200+Y). 38 3400+100 Y=7600+38 Y 62 Y=4200 Y=67, 7 гр.
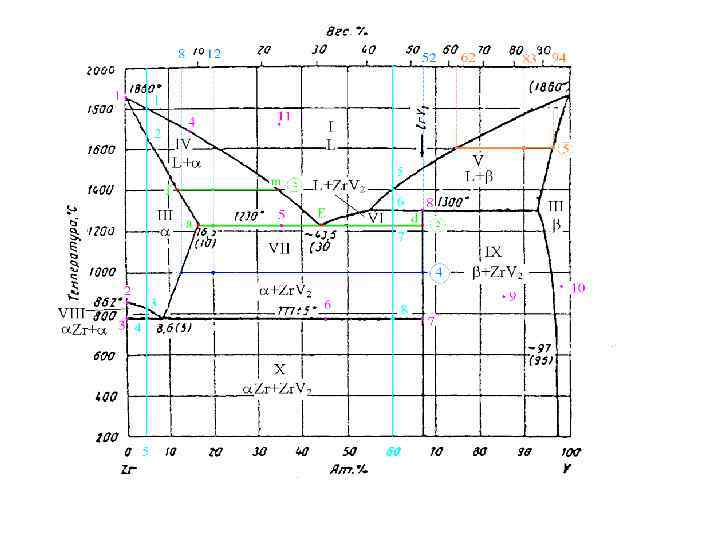

6. Определите число термодинамических степеней свободы в точках, указанных преподавателем. • Точка 1. К=1 (Zr), Ф=2 (Zr-твердый, Zr-жидкий), С=12+1=0. • Точка 2. К=1 (Zr), Ф=2 ( -Zr, -Zr), С=1 -2+1=0. • Точка 3. К=1 (Zr), Ф=1 (Zr-твердый), С=1 -1+1=1. • Точка 4. К=2 (Zr, V), Ф=2 (L, ), С=2 -2+1=1. • Точка 5. К=2 (Zr, V), Ф=3 (L, , Zr. V 2), С=2 -3+1=0. • Точка 6. К=2 (Zr, V), Ф=3 (Zr, , Zr. V 2), С=2 -3+1=0. • Точка 7. К=1 (Zr. V 2), Ф=1 (Zr. V 2 – твердый), С=1 -1+1=1. • Точка 8. К=2 (Zr, V), Ф=3 (L, , Zr. V 2), С=2 -3+1=0. • Точка 9. К=2 (Zr, V), Ф=2 ( , Zr. V 2), С=2 -2+1=1. • Точка 10. К=2 (Zr, V), Ф=1 ( ), С=2 -1+1=2. • Точка 11. К=2 (Zr, V), Ф=1 (L), С=2 -1+1=2.
Содержание материала
- Фаза колебаний
- Видео
- Что такое разность фаз
- Как найти разность фаз колебаний, формула
- Пружинный маятник
- Амплитуда и фаза колебаний
- Что такое начальная фаза и как определить ее по графику колебаний
- Как вычислить начальный угол по интервалу смещения
- Сложение колебаний и начальная фаза
- Характеристики колебаний
- Фазы колеблющейся величины, ее скорости и ускорения
- Что мы узнали?
- Звук
Фаза колебаний
- Подробности
- Просмотров: 833
Фаза колебаний (φ) характеризует гармонические колебания. Выражается фаза в угловых единицах — радианах.
При заданной амплитуде колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса: φ = ωt.
Фаза колебаний определяет при заданной амплитуде состояние колебательной системы (значение координаты, скорости и ускоренияв) любой момент времени.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Видео
Как найти разность фаз колебаний, формула
Пусть имеется два гармонических колебания, изменяющихся по одному закону и с одинаковой амплитудой и частотой, т.е Xm1=Xm2иω1=ω2. Такие колебания будут отличаться друг от друга только значением начальных фаз.
Запишем уравнение колебаний для каждого:x1=Xm1·sinω1·t+φ01и x2=Xm2·sinω2·t+φ02. Введем обозначение для разности фаз — ∆φ. Так как амплитуда и частота равны, то ∆φ определяется выражением:
∆φ=φ02—φ01.
На рисунке показаны два графика гармонических колебаний, разность фаз которых составляет π радиан.
Разность фаз также называют сдвигом фаз.
Колебания, разность фаз которых не зависит от времени, называются когерентными.
Рассмотрим два гармонических когерентных колебания с одинаковым периодом и направлением:x1=Xm1·cosω·t+φ01иx2=Xm2·cosω·t+φ02. Величину результирующей амплитуды X_m определим по правилу сложения векторов: Xm2=Xm12+Xm22+2·Xm1·Xm2·cosφ02—φ01. Из формулы видно, что суммарная амплитуда колебаний зависит от сдвига фаз. Приведем два варианта:
- Сдвиг фаз равен четному числу π:,2π,4π,6π и т.д. В этом случае: cosφ02—φ01=1. Суммарная амплитуда: Xm=Xm1+Xm2. Такие колебания называют синфазными. Пример синфазных колебаний приведен на рисунке.
- Сдвиг фаз равен нечетному числу π:π,3π,5π и т.д. В этом случае: cosφ02—φ01=—1. Суммарная амплитуда: Xm=Xm1—Xm2. О таких колебаниях говорят, что они находятся в противофазе. Если Xm1=Xm2,тоXm=. Пример двух противофазных колебаний с одинаковыми амплитудами приведен на рисунке.
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости. Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
![T — период [с]](https://2cheloveka.ru/files/8a8b705a8ca6a17ca607a91873e3d3ab/9579ce08de007dbc87410b253dbf8912.png)
T — период [с]
m — масса маятника [кг]
k — жесткость пружины [Н/м]
π = 3,14
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия. Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени. Обозначение – ( varphi ), единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний. Фаза гармонических колебаний в процессе колебаний изменяется. ( varphi_0 ) – начальная фаза колебаний. Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно! Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Сложение колебаний и начальная фаза
Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.
Допустим, что два колебания с равными частотами происходят по одной прямой. Уравнением результирующих колебаний будет выражение:
тогда амплитуда суммарного колебания равна:
где $A_1$; $A_2$ – амплитуды складывающихся колебаний; $<varphi >_2;;<varphi >_1$ – начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:
Уравнение траектории точки, которая принимает участие в двух взаимно перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами $<varphi >_2и<varphi >_1$:
В случае равенства начальных фаз составляющих колебаний уравнение траектории имеет вид:
что говорит о движении точки по прямой линии.
Если разность начальных фаз складываемых колебаний составляет $Delta varphi =<varphi >_2-<varphi >_1=frac<pi ><2>,$ уравнением траектории становится формула:
что означает, траектория движения эллипс.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
T — период [с]
t — время [с]
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
ν — частота [Гц]
t — время [с]
T — период [с]
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.
Она используется в уравнении гармонических колебаний:

Фазы колеблющейся величины, ее скорости и ускорения
Возьмем первую производную от параметра $xi $, совершающего гармонические колебания:
Тогда вторая производная от $xi $ задается функцией:
Уравнения (2) и (3) показывают, что скорость и ускорение $xi $ совершают гармонические колебания с циклической частотой ${omega }_0$. Амплитуды данных колебаний равны:
Фаза скорости (${omega }_0t+varphi +frac{pi }{2}$) отличается от фазы ускорения (${omega }_0t+varphi +pi $) на величину равную $frac{pi }{2}$. Фаза ускорения отлична от фазы колеблющейся величины на $pi $. Это значит, что в тот момент времени, когда $xi =0$ скорость ее изменения ($frac{dxi }{dt}$) становится максимальной. При $xi $ равной наибольшему значению меньшему нуля, ее ускорение превращается в максимальное положительное.
Что мы узнали?
Фаза колебания — это аргумент гармонической функции в ее формуле. Фактически это конкретный момент колебания. Начальная фаза — это аргумент в нулевой момент времени. Наибольшее значение начальная фаза колебаний играет при сравнении различных колебаний с одинаковой частотой.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Теги
Как найти массу если известна скорость ?
- Следить
- Отметить нарушение!
Ответы и объяснения
Есть, к примеру, второй закон Ньютона. Согласно ему имеет место формула:
F = m*a, где F – сила, приложенная к телу, m – масса тела и a – ускорение
Ускорение можно найти по следующей формуле:
a = ν / t, где ν – скорость, t – время
Подставим формулу ускорения в формулу Ньютона:
F = (m*ν) / t
- 1 комментарий
- Отметить нарушение!
- Спасибо 0
