Как найти массу фотоэлектронов

Ягма Медицинская физика

Педиатрический
факультет

1 курс

2 Семестр Лекция №

«Элементы квантовой
оптики.

Физика
фотоэффекта»

Составил: Колпаков
В.А.

2004 г.

I. Фотоэффект и его виды. Основные законы внешнего фотоэффекта.

Фотоэффект
представляет собой одну из разновидностей
фотоэлектрических явлений.

Фотоэлектрические
явления –
это
явления взаимного превращения лучистой
и электрической энергии в фотоэлектрической
цепи.

Физически
фотоэффект представляет собой процесс
полного или частичного освобождения
заряженных частиц в веществе при
поглощении им лучистой энергии (фотонов).

B
результате наблюдается:

• Изменение
электропроводности вещества;

• Эмиссия
электронов из вещества;

• Возникновение
фотоэлектродвижущей силы на границе
веществ с разным типом проводимости.

Виды фотоэффекта:

1. Внешний
фотоэффект. Внутренний фотоэффект
изменения проводимости (положительный
и отрицательный).

2. Внутренний
фотогальванический фотоэффект (вентильный
фотоэффект, фотоэффект в запирающем
слое).

3. Фотопьезоэффект.

4. Фотодиэлектрический
эффект.

5. Фотоэлектромагнитный
эффект.

В медицинской
аппаратуре чаще всего используется
внешний внутренний эффект изменения
проводимости и фотоэффект в запирающем
слое.

Внешний
фотоэффект –
это
явление (процесс) эмиссии электронов
из вещества в вакуум или другое вещество
под действием электромагнитного
излучения.

Внутренний
фотоэффект изменения проводимости –
это изменение электрического сопротивления
полупроводника при поглощении им
электромагнитного излучения (фотонов).

Фотогальванический
(вентильный) эффект –
это
явление возникновения фотоэлектродвижущей
силы (фотоЭДС) на границе раздела
полупроводников или других носителей
электрических зарядов электрическим
полем.

Законы внешнего
фотоэффекта и их характеристика.

Внешний
фотоэффект был открыт в 1887 году
ученым Герцем, исследован в 1888-89г
русским физиком Столетовым, и на
основе квантовых представлений объяснен
в 1905 году Эйнштейном. Законов фотоэффекта
три:

1. Закон Столетова.

2. Закон
Эйнштейна-Ленарда.

3. Закон «красной
границы» фотоэффекта.

Закон
Столетова имеет
теоретическую и техническую формулировку.

Теоретическая
формулировка:

Количество
испускаемых электронов пропорционально
плотности падающего на вещество лучистого
потока (облученности) при его неизменном
спектральном составе.

Техническая
формулировка (‘справедлива только для
вакуумных фотоэлектронных приборов,
например, вакуумных фотоэлементов)

Фототок насыщения
прямо пропорционален лучистому потоку
и равен ему при введении коэффициента,
который называется коэффициент
интегральной чувствительности (к
источнику типа А).

Формула закона:

I_н~Ф
= к*Ф

Где
I_Н
– фототек насыщения вакуумного фотоэлемента
(мкА) Ф – лучистый поток (Вт, Лм) к –
коэффициент интегральной чувствительности,
мкА/Вт, мкА/Лм

Для выполнения
закона нужно, чтобы спектральный состав
падающего лучистого потока был неизменным,
напряжение на фотоэлементе должно быть
постоянным. При больших лучистых потоках
закон не соблюдается.

Закон Эйнштейна
– Ленарда

Устанавливает
зависимость между энергиями падающих
фотонов и испускаемых веществом
фотоэлектронов. Закон Эйнштейна
представляет собой частный случай
закона сохранения энергии.

Формулировка
закона:

Максимальная
начальная кинетическая энергия
фотоэлектронов возрастает прямо
пропорционально с частотой падающего
фотоэлектрически активного лучистого
потока и не зависит от его

интенсивности.

Формула закона:

(m_эV_э²/2)_max
~ hv

В
формуле m_э
– масса фотоэлектрона

V_э
–
скорость фотоэлектрона

h
– постоянная Планка

υ
– частота излучения

hυ
– энергия фотонов лучистого потока

Закон «красной
границы» фотоэффекта

Устанавливает
условия возможности фотоэффекта для
данного вещества в зависимости от работы
выхода электронов из данного вещества
и энергии падающих на вещество фотонов
лучистого потока.

Формулировка:

Для каждого вещества
в спектре падающего лучистого потока
существует такая длина волны, за пределами
которой фотоэффект не происходит.

Эта
длина волны
λ0,
и соответствующая ей частота υ₀
называются длинноволновой или «красной»
границей фотоэффекта.

Физически наличие
красной границы фотоэффекта объясняется
тем, что каждое вещество имеет определенное
значение работы выхода фотоэлектронов
Авых.

Каждому
фотону падающего на вещество лучистого
потока соответствует своя энергия hυ,
частота υ
и длина волны λ.

Если работа выхода
электронов из вещества меньше энергии
падающих фотонов, то фотоэффекта не
будет.

Если эта энергия
больше, то фотоэффект осуществим, причем
избыток энергии тратится на кинетическую
энергию фотоэлектронов.

Если работа выхода
фотоэлектронов равна энергии падающих
фотонов, фотоэффект осуществится, но с
нулевой кинетической энергией выбитых
фотоэлектронов.

Данному
соотношению работы выхода и энергии
фотона и соответствует — «красная
граница» фотоэффекта по частоте υ₀

и
длине
волны λ0.

Авых
=
hυ₀
= h_c/
λ0
;
υ₀
= Авых
/ h
; λ0

– h_c
/ Авых

Например,
для калия Авых
⁼
2,01 – 1,74 электрон-Вольта, что соответствует
по длине волны “красной границе”
λ₀
612 – 710 нанометров (нм).

П. Уравнение
Эйнштейна и его применение для объяснения
законов фотоэффекта.

Закон Эйнштейна
на основе квантовых представлений
объясняет законы фотоэффекта, и является
частным случаем закона сохранения
энергии для фотоэлектрических явлений.

В своих теоретических
построениях Эйнштейн исходил из
наблюдения Ленарда, Томсона и Милликена
(1899 – 1900 гг) о зависимости энергии
фотоэлектронов от частоты (но не
интенсивности) падающего лучистого
потока, и гипотезы Планка (1900г) о квантовой
природе излучения энергии веществом.

Эйнштейн ввел
понятие фотона и дополнил учение Планка
тем, что ввел постулат о квантовой
природе не только излучения энергии,
но и ее распространения и поглощения
веществом.

В основе постулата
Эйнштейна три положения:

1. При взаимодействии
с электронами вещества падающие
фотоны полностью поглощаются.

2. Один фотон
взаимодействует только с одним электроном.

3. Один поглощенный
фотон может выбросить только один
фотоэлектрон с некоторой кинетической
энергией.

Формулировка
закона Эйнштейна:

При фотоэффекте
энергия фотона расходуется на работы
выхода электрона из вещества и на его
кинетическую энергию, которая будет
максимальной тогда, когда электрон
испускает с поверхности вещества.

Объяснение
законов фотоэффекта на основе уравнения
Эйнштейна

Объяснение
закона Столетова: С
квантовых
позиций лучистый поток определяется
количеством фотонов, падающих за единицу
времени на поверхность вещества. Фототок
насыщения определяется количеством
испускаемых в единицу времени
фотоэлектронов. Поэтому, в соответствии
с постулатом Эйнштейна, чем больше
лучистый фотонный поток, тем большим
будет фотоэлектронный ток.

Объяснение
закона Эйнштейна: Энергия
падающих фотонов лучистого потока
определяется его частотой. Так как
работа выхода фотоэлектронов для данного
вещества постоянна, то с увеличением
энергии фотонов большая ее часть тратится
на кинетическую энергию выбиваемых
электронов.

Объяснение
закона «красной границы»: С
уменьшением частоты падающего лучистого
потока уменьшается энергия фотонов.
Когда энергия фотона будет равна работе
выхода фотоэлектронов из данного
вещества, они останутся на поверхности
этого вещества с «нулевой» кинетической
энергией. При дальнейшем уменьшении
энергии фотонов фотоэффекта не будет,
так как энергии фотона будет недостаточно
для совершения работы выхода фотоэлектрона
из данного вещества (υ_ф<
υ_min).

III.
Фотоэффект в запирающем слое. Устройство,
принцип работы, особенности селенового
фотоэлемента.

Фотоэффект
в запирающем слое является
разновидностью

внутреннего
фотоэффекта. Он заключается
в
возникновении

фотоэлектродвижущей
силы (фотоЭДС) между
металлом
и

полупроводником
или между полупроводниками
разных
типов проводимости.

Механизм вентельного
фотоэффекта:

Возьмем
металл и полупроводник «n»
– типа при условии, что работы выхода
электронов из полупроводника меньше,
чем из металла.

авых
полупр <
авых
мет

При соприкосновении
металла и полупроводника произойдет
диффузия электронов из полупроводника
в металл через границу контакта и
приконтактный участок полупроводника
вследствие убыли электронов зарядится
положительно по отношению к металлу,
то есть возникнет контактная разность
потенциалов (КПР).

Под действием
лучистой энергии (видимого света,
инфракрасного, ультрафиолетового
излучения, рентгеновских лучей) электроны
полупроводника получат дополнительную
энергию, их подвижность увеличится и,
поэтому, КПР возрастает.

Изменение КПР
происходит пропорционально облученности
контактного слоя и называется
фотоэлектродвижущей силой (фотоЭДС).

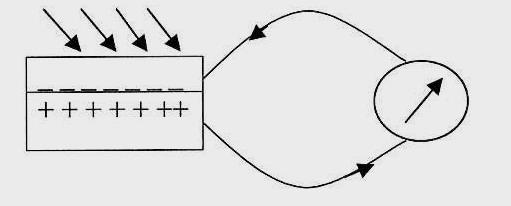
____________ – металл

+ + + + + ++ – полупроводник

Если подключить
к металлу и полупроводнику измерительный
прибор, то при освещении контактного
слоя в цепи возникнет электрический
ток, который называется фототек.

Фотоэффект в
запирающем слое лежит в основе работы
селеновых фотоэлементов и солнечных
батарей.

Устройство,
принцип работы и особенности селенового
элемента.

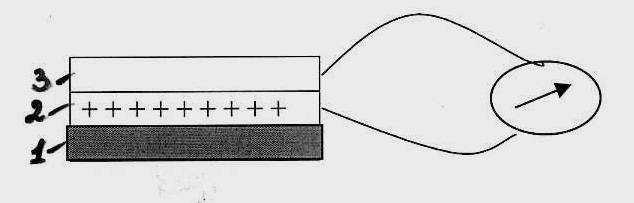
Селеновый элемент
представляет собой круглую или
прямоугольную пластмассовую пластину
(1), на которую напыляется слой селена
(2). На селеновый слой напыляется очень
тонкий, а поэтому прозрачный слой металла
(3). Граница раздела металла и селена
называется запирающим слоем, так как
он пропускает носителя зарядов (электроны)
только в одном направлении.

Так как работа
выхода электронов из селена меньше, чем
из металла, электроны из селена переходят
в металл. При этом селен заряжается
положительно по отношению к металлу,
то есть образуется контактная разность
потенциалов.

При
освещении контактного слоя электроны
селена приобретают дополнительную
энергию, и в большем количестве
перемещаются в металл. Контактная
разность потенциалов, а, следовательно,
и электродвижущая сила возрастают, и
образуют при замыкании цепи между
металлом и селеном электрический
фототек.

Особенности
селенового элемента:

1. Селеновый элемент
является генератором фотоЭДС и тока, и
поэтому не требует источников питания.

2. Зависимость
фототока селенового элемента от
его облученности

линейная, что очень
удобно для измерительных цепей.

3. Кривая спектральной
чувствительности селенового элемента
практически совпадает с кривой
спектральной чувствительности глаза
человека для дневного зрения и поэтому
селеновый элемент реагирует на свет
так же, как человеческий глаз.

По этой причине
селеновый элемент широко используется
в качестве датчиков измерительных
приборов, регистрирующих уровни яркости
и освещенности в гигиене, светотехнике
и фотографии (люксметры, экспонометры).

Соседние файлы в папке Медицинская физика

• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнение Эйнштейна для фотоэффекта.

Эйнштейн в 1905 г. дал объяснение фотоэффекта, развив идею Планка о преры­вающемся испускании света:

Исходя из заявления Эйнштейна, из явления фотоэффекта вытекает, что свет имеет прерывистую структуру: излученная порция световой энергии E = hv сохраняет свою ин­дивидуальность и далее. Поглотиться может лишь вся порция полностью. Эта порция имеет название фотона.

Если фотон передает электрону энергию hv, которая является больше или равной величине работы А по удале­нию электрона с поверхности металла, значит, электрон покидает поверхность этого металла. Разность между hv и А приводит к образованию кинетической энергии электрона. Следствие из закона сохранения энергии:

.

Эта формула является уравнением Эйнштейна, которое описывает каждый из законов фотоэффекта. Следствием из уравнения Эйнштейна является то, что кинетическая энергия электрона линейно зависит от частоты v и никак не зависит от интенсивности излучения. Так как общее число электронов n, которые покидают по­верхность металла, пропорционально числу падающих фотонов, значит, величина n оказывается пропорциональной интенсивности падающего излучения.

Красную границу фотоэффекта можно получить из , если скорость электрона, который покидает металл, приравнять к нулю:

,

то есть красная граница фотоэффекта зависит лишь от работы выхода А. С учетом того, что , из получаем значение предельной длины волны:

.

При длинах волн, больших λ_min, то есть расположенных ближе к красным волнам, фотоэффект не наблюдается. Именно поэтому и появилось название предельной длины волны λ_min — красная граница фотоэффекта.

Фотоэффект

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.

Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.

Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.

Опыты Столетова

В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1 .

Рис. 1. Фотоэлемент Столетова

В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод . На катод и анод подаётся напряжение, величину которого можно менять с помощью потенциометра и измерять вольтметром .

Сейчас на катод подан «минус», а на анод — «плюс», но можно сделать и наоборот (и эта перемена знака — существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод (Поэтому поданное на электроды напряжение часто называют анодным напряжением). В данном случае, например, напряжение положительно.

Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением и летят на анод. Включённый в цепь миллиамперметр регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.

В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.

Зависимость фототока от напряжения

Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2 .

Рис. 2. Характеристика фотоэлемента

Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .

Если напряжение отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает — электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод:

Здесь кг — масса электрона, Кл — его заряд.

Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.

Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:

Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.

При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.

При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!

Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.

Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.

Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.

Законы фотоэффекта

Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.

Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).

Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.

А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.

Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3 ):

Рис. 3. Зависимость энергии фотоэлектронов от частоты света

Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если , то фотоэффекта нет.

Если же nu_0′ alt=’nu > nu_0′ /> , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.

Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при nu_0′ alt=’nu > nu_0′ /> : максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.

Все эти факты нашли отражение во втором и третьем законах фотоэффекта.

Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При фотоэффект не наблюдается ни при какой интенсивности света.

Трудности классического объяснения фотоэффекта

Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?

Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.

В переменном электрическом поле световой волны электрон начинает совершать колебания.

И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.

Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.

Далее, откуда берётся красная граница фотоэффекта? Чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растёт и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.

Кроме того, неясна безынерционность фотоэффекта. Именно, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды.

Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.

Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.

Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.

Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.

Гипотеза Планка о квантах

Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).

Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.

В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.

Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:

Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.

Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:

Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.

Уравнение Эйнштейна для фотоэффекта

Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.

Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .

Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.

Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .

Каждый фотон монохроматического света, имеющего частоту , несёт энергию .

Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.

Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.

Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода по извлечению электрона из вещества и на придание электрону кинетической энергии :

Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.

Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.

Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.

Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности.

Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.

Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.

1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.

Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.

2. Выразим из формулы (4) кинетическую энергию:

Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.

Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3 .

3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота , определяемая равенством

как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.

Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.

Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.

В ходе таких опытов было получено значение , в точности совпадающее с (3) . Такое совпадение результатов двух независимых экспериментов — на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта — означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике — теории микромира, построение которой продолжается и сегодня.

Фотоэффект. Фотоны

В 1887 году Г. Герцем был открыт фотоэлектрический эффект, а продолжить его исследования довелось А.Г. Столетову. Ф. Леонард в 1900 году серьезно занялся данным проектом. К тому времени был открыт электрон. Это говорило о том, что фотоэффект состоял в вырывании электронов из вещества под действием падающего на него света.

Данное исследование законов Столетова изображено на рисунке 5 . 2 . 1 .

Рисунок 5 . 2 . 1 . Схема экспериментальной установки для изучения фотоэффекта.

В лабораторных условиях применили стеклянный вакуумный баллон с двумя металлическими электродами с очищенной поверхностью. К ним прикладывали напряжение U с возможностью изменения полярности с помощью ключа. Катод освещали монохроматическим светом с длиной волны λ через кварцевое окошко. Так как световой поток оставался неизменным, то зависимость силы тока I от напряжения ослабевала. Рисунок 5 . 2 . 2 . наглядно демонстрирует кривые зависимости при интенсивном свете, попадающем на катод.

Рисунок 5 . 2 . 2 . Зависимость силы фототока от приложенного напряжения. Кривая 2 соответствует большей интенсивности светового потока. I н 1 и I н 2 – токи насыщения, U з – запирающий потенциал.

По графику видно, что при подаче большого напряжения фототок анода А достигает насыщения, потому как при вырывании светом из катода они в состоянии достичь его.

Ток насыщения. Закономерности фотоэффекта

Ток насыщения I н прямо пропорционален интенсивности падающего света.

При наличии отрицательного напряжения на аноде, электрическое поле, находящееся между катодом и анодом, тормозится электронами. К аноду могут добраться электроны, у которых кинетическая энергия превышает значение | e U | . При наличии напряжения меньше, чем – U з , происходит прекращение фототока. После измерения – U з определяется максимальная кинетическая энергия фотоэлектронов:

m υ 2 2 m a x = e U 3 .

Из формулы видно, что оно не зависит от интенсивности падающего света. После глубоких исследований стало ясно, что при возрастании запирающего потенциала происходит линейное увеличение частоты света ν .

Рисунок 5 . 2 . 3 . Зависимость запирающего потенциала U з от частоты ν падающего света.

После многочисленных экспериментов были установлены закономерности формул фотоэффекта:

1. При увеличении частоты света ν происходит возрастание кинетической энергии, независящей от ее интенсивности.
2. Наименьшей частотой ν m i n с внешним фотоэффектом называют красную границу фотоэффекта каждого вещества.
3. Количество фотоэлектронов за 1 с вырывания из катода прямо пропорционально интенсивности света.
4. Фотоэффект возникает после освещения катода с условием, что ν > ν m i n _.

Данные закономерности не соответствовали представлениям классической физики о взаимодействии света с веществом. Исходя из волновых представлений, взаимодействие световой волны с электроном должно действовать по принципу постепенного накапливания энергии. Чтобы он смог вылететь из катода, необходимо иметь достаточное количество энергии, накапливаемой за определенный промежуток времени, не зависящий от интенсивности света.

Появление фотоэлектронов происходит сразу после освещения катода. Данная модель не давала четкого представления нахождения красной границы фотоэффекта. Волновая теория света не могла дать объяснение независимости энергии фотоэлектронов от интенсивности светового потока и пропорциональности максимальной кинетической энергии частоты света. Поэтому электромагнитная теория была не способна объяснить эти изменения.

В 1905 году А. Эйнштейн дает теоретическое объяснение наблюдаемых закономерностей фотоэффекта, основываясь на гипотезе М. Планка.

Постоянная Планка. Уравнение Эйнштейна

Излучение и поглощение света происходит определенными порциями, где она определяется формулой E = h ν , h принято называть постоянной Планка.

Основной шаг в развитии квантовых представлений относится к Эйнштейну:

Свет обладает прерывистой структурой. Электромагнитная волна состоит из порций, называемых, кварками, спустя время которые зафиксировали как фотоны.

После взаимодействия с веществом фотон передает свою энергию h ν одному электрону, одна часть которой рассеивается при столкновениях с атомами, а другая затрачивается на преодоление потенциального барьера на границе металл-вакуум. Для этого ему необходимо совершить работу выхода А , зависящую от свойств материала катода.

Наибольшую кинетическую энергию, вылетевшую из катода фотоэлектроном, определяют законом сохранения энергии:

m ν 2 2 m a x = e U e = h ν – A .

Формула получила название уравнения Эйнштейна для фотоэффекта.

Благодаря ему, закономерности внешнего явления фотоэффекта могут быть объяснены.

Линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, существование красной границы, безынерционность фотоэффекта следуют из данного выражения.

Общее количество фотоэлектронов, которые покидают поверхность катода в течение 1 с , пропорционально числу фотонов, падающих на поверхность. Можно сделать вывод, что ток насыщения должен быть прямо пропорционален интенсивности светового потока.

По уравнению фотоэффекта Эйнштейна тангенс угла наклона прямой, выражающий зависимость запирающего потенциала U з от частоты ν , равняется отношению постоянной Планка h к заряду электрона e :

Формула позволяет вычислить значение постоянной Планка.

Р. Милликенн проводил измерения в 1914 году, после чего смог определить работу выхода А :

A = h ν m i n = h c λ к р ,

где c – скорость света, λ к р – длина волны, которая соответствует красной границе фотоэффекта.

Большинство металлов имеет работу выхода А и составляет несколько электрон-вольт ( 1 э В = 1 , 602 · 10 – 19 Д ж ) .

Квантовая физика использует электрон-вольт как энергетическую единицу измерения. Тогда значение постоянной Планка равняется

h = 4 , 136 · 10 – 15 э В · с .

Наименьшая работа выхода наблюдается у щелочных элементов. Натрий при A = 1 , 9 э В соответствует красной границе фотоэффекта λ к р ≈ 680 н м . Такие соединения применяют для создания катодов в фотоэлементах, используемых для регистрации видимого света.

Законы фотоэффекта говорят о том, что при пропускании и поглощении свет ведет себя подобно потоку частиц, называемых фотонами или световыми квантами.

Энергия фотонов записывается в виде формулы E = h ν .

При движении в вакууме фотон обладает скоростью с , а его масса m = 0 . Общее соотношение теории относительности, связывающее энергию, импульс и массу любой частицы, записывается как E 2 = m 2 c 4 + p 2 c 2 .

Отсюда следует, что фотон обладает импульсом, значит:

Можно сделать вывод, что учение о свете вернулось к представлениям о световых частицах – корпускулах. Но это не расценивается как возврат к корпускулярной теории Ньютона. В XX было известно о двойственной природе света. Когда он распространялся, то проявлялись его волновые свойства (интерференция, дифракция, поляризация), при его взаимодействии с веществом – корпускулярные, то есть явление фотоэффекта. Это и получило название корпускулярно-волнового дуализма.

Спустя время, данная теория была подтверждена у других элементарных частиц. Классическая физика не дает наглядную модель сочетаний волновых и корпускулярных свойств микрообъектов. Их движениями управляют законы квантовой механики. В основе этой науки лежит теория абсолютно черного тела, доказанная М. Планком, и квантовая, предложенная Эйнштейном.

Рисунок 5 . 2 . 4 . Модель фотоэффекта

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/fizika/fotoeffekt/

http://zaochnik.com/spravochnik/fizika/kvantovaja-fizika/fotoeffekt-fotony/

[/spoiler]

Физика, 11 класс

Урок 22. Фотоэффект

Перечень вопросов, рассматриваемых на уроке:

• предмет и задачи квантовой физики;
• гипотеза М. Планка о квантах;
• опыты А.Г. Столетова;
• определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
• уравнение Эйнштейна для фотоэффекта;
• законы фотоэффекта.

Глоссарий по теме:

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Фотоэффект – это вырывание электронов из вещества под действием света.

Квант – (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.

Ток насыщения – некоторое предельное значение силы фототока.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.

Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.

3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.

4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.

Теоретический материал для самостоятельного изучения

В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.

Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.

Коэффициент пропорциональности получил название постоянной Планка, и она равна:

h = 6,63 ∙ 10^-34 Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.

В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.

Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.

Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта

Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения

Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.

Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.

Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.

hν_min = A_в

где А_в – работа выхода электронов;

h – постоянная Планка;

ν_min – частота излучения, соответствующая красной границе фотоэффекта;

с – скорость света;

λкр – длина волны, соответствующая красной границе_.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.

Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Задерживающее напряжение

Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:

где – максимальная кинетическая энергия электронов;

Е – заряд электрона;

– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:

В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».

Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий

1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода	Запирающее напряжение

Решение:

Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.

Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:

Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

Ответ:

Работа выхода	Запирающее напряжение
не изменится	увеличится

2. Красная граница фотоэффекта для вещества фотокатода λ₀ = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.

Решение.

Запишем уравнение для фотоэффекта через длину волны:

Условие связи красной границы фотоэффекта и работы выхода:

Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:

Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:

Подставляя численные значения, получаем: λ ≈ 215 нм.

Ответ: λ ≈ 215 нм.

В сегодняшней статье нашей традиционной рубрики «физика» разбираем задачи на фотоэффект.

Подпишитесь на наш телеграм и не пропускайте важные новости. А на втором канале ищите скидки и приятные бонусы для клиентов.

Задачи на фотоэффект с решениями

Прежде чем приступать к решению задач, напоминаем про памятку и формулы. Эти материалы пригодятся при решении задач по любой теме.

Задача на фотоны и фотоэффект №1

Условие

Найти энергию фотона ε (в Дж) для  электромагнитного излучения с частотой ϑ=100·1014Гц.

Решение

Это типичная задача на энергию фотона. Применим формулу:

ε=hcλ=hϑ

Здесь h – постоянная Планка. Произведем расчет:

ε=6,63·10-34·10·1014=6,63·10-18Дж

Ответ: ε=6,63·10-18 Дж.

Задача на фотоны и фотоэффект №2

Условие

При фиксированной частоте падающего света в опытах №1 и №2 получены вольтамперные характеристики фотоэффекта (см. рис.). Величины фототоков насыщения равны I1 и I2, соответственно. Найти отношение числа фотоэлектронов N1 к N2 в этих двух опытах.

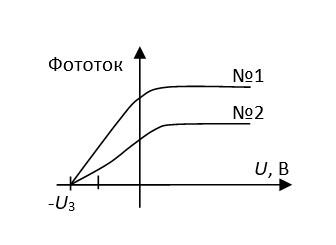
I1=13,5 мкАI2=10,6 мкА

Решение

Вольтамперная характеристика фотоэффекта показывает зависимость тока от напряжения между электродами. При выходе тока на насыщение все фотоэлектроны, выбитые из фотокатода, попадают на анод. Таким образом, величина тока насыщения пропорциональна числу фотоэлектронов. Тогда:

N1N2=I1I2=13,510,6=1,27

Ответ: 1,27.

Задача на фотоны и фотоэффект №3

Условие

На поверхность металла падают монохроматические лучи с длиной волны 0,1 мкм. Красная  граница фотоэффекта 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? 

Решение

Энергия падающего фотона равна:

ε=hcλ

Далее для решения задачи примененим уравнение Эйнштейна для фотоэффекта, которое можно записать в виде:

hcλ=hcλ0+Eк

Отсюда найдем кинетическую энергию:

Eк=hcλ-hcλ0=hcλ0-λλλ0

Чтобы найти искомую долю, разделим кинетическую энергию на энергию фотона:

W=Eкε=hcλ0-λλhc·λλ0=λ0-λλ0=3·10-7-10-73·10-7=0,667

Ответ: W=0,667.

Задача на фотоны и фотоэффект №4

Условие

Максимальная энергия фотоэлектронов, вылетающих из металла при его освещении лучами с длиной волны 325 нм, равна Tтax=2,3·10-19Дж. Определите работу выхода и красную границу фотоэффекта. 

Решение

Формула Эйнштейна для фотоэффекта имеет вид:

hϑ=hcλ=A+Tmax

Отсюда работа выхода A равна:

A=hcλ-Tmax

Красная граница фотоэффекта определяется условием Tmax=0, поэтому получаем:

A=hcλ0λ0=hcA

Найдем:

A=6,63·10-34·3·1083,25·10-7-2,3·10-9=3,81·10-19 Дж

λ0=6,63·10-34·3·1083,81·10-19=520 нм

Ответ: A=3,81·10-19Дж; λ0=520 нм.

Задача на фотоны и фотоэффект №5

Условие

Наибольшая длина волны света λ0, при которой еще может наблюдаться фотоэффект на сурьме, равна 310 нм. Найдите скорость электронов, выбитых из калия светом с длиной волны 140 нм. 

Решение

Красная граница фотоэффекта определяется условием Tmax=0, поэтому для работы выхода получаем:

A=hcλ0

Формула Эйнштейна для фотоэффекта имеет вид:

hcλ=A+Tmax

Учитывая, что Tmax=mv2max2, определим максимальную скорость электронов при фотоэффекте:

vmax=2hcm1λ-1λ0

Произведем вычисления:

vmax=2·6,63·10-349,1·10-3111,4·10-7-13,1·10-7=1,3·106 мс

Ответ: 1,3·106 мс.

Вопросы с ответами на тему «Фотоны и фотоэффект»

Вопрос 1. В чем суть фотоэффекта?

Ответ. Фотоэффект — это явление «выбивания» электронов из вещества под действием света (электромагнитного излучения).

Вопрос 2. Что такое ток насыщения?

Ответ. Ток насыщения при фотоэффекте — максимальное значение фототока.

Вопрос 3. Что такое красная граница фотоэффекта?

Ответ. Это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Вопрос 4. Что такое работа выхода?

Ответ. Это минимальная энергия, которую надо сообщить электрону, чтобы выбить его из металла.

Вопрос 5. Что такое квант?

Ответ. Неделимая порция какой-либо величины в физике.

Нужна помощь в решении задач и выполнении других типов заданий? Обращайтесь в профессиональный сервис для учащихся по любому вопросу.