поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
У многих учащихся возникают трудности с решением задач, связанных со вращательным движением тел. Также вызывают стопор задачи с блоками. В основном я это понял во время занятий физикой со своими школьниками и студентами. Поэтому я решил написать статью, в которой рассматриваю 7 случаев с небольшими задачами по динамике блоков. Это те основные кирпичики, из которых складываются все типы задач с блоками. В том числе и олимпиадные. Все примеры представлены от простого к сложному. Приятного чтения 🙂
А пока попрошу подписаться на канал в telegram IT mentor . Автор пишет краткие заметки и наблюдения по физике, математике, программированию, железу и технике 💡
Случай 1
Рассмотрим самый простой случай. Идеальная веревка перекидывается через неподвижный идеальный блок. Мы пытаемся удержать груз, прикрепленный на одном конце веревки, с помощью прикладывания силы F на другом конце веревки. Сначала рассмотрим статическое равновесие. Будем определять силу F, которую нам необходимо прикладывать.
Пожалуй, что из задач с блоками этот пример является самым простым. Допущения, принятые здесь, вполне согласуются с реальной жизнью. Но всё таки это сильно упрощенная модель.
1. Выигрыша в силе мы не имеем;
2. На какое расстояние сдвинули веревку, на такое же расстояние поднимется груз;
3. Удобство поднятия груза заключается в выборе направления тяги.
Случай 2
Немного усложним нашу ситуацию, добавив в систему ускорение. Какую силу нужно приложить, чтобы поднять груз с ускорением? Здесь также будем учитывать, что веревка идеальная:
нерастяжимая — поэтому все ускорения равны
невесомая — поэтому для правого конца выполняется условие F = T (для нулевой массы веревки).
Случай 3
Будем продолжать усложнение конфигурации из грузов и блоков. Что если в систему добавить второй блок, который будет висеть на веревке, один конец которой будет подвешен к потолку, а другой конец протянут через неподвижный блок и в итоге удержан нашей силой F. Рассмотрим статической равновесие системы и попробуем найти силу F. Теперь в задаче появляются две веревки:
Первая короткая нить удерживает груз (на рисунке изображена желтым цветом). Вторая длинная нить протянута через блоки, один конец закреплен в потолке, а другой конец удерживается силой F (на рисунке нить обозначена оранжевым цветом).
Мы получили выигрыш в силе в два раза. Простыми словами объяснить это можно так: 50 кг мы сможем удержать, тянув за свободный конец оранжевой веревки так, как будто мы бы удерживали 25 кг в ситуации с одним неподвижным блоком (Случай 1).
Как-то раз, занимаясь в тренажерном зале, я обратил внимание на разговор двух своих друзей. Они рассуждали, что поднимали на бицепс 70 кг в тренажере (так было написано на плитках, когда вставляешь штырек в определенный вес). Мне было интересно и я спросил: «Если в тренажере вы поднимаете 70 кг на бицепс, то почему же не можете поднять штангу в 70 кг также на бицепс?». Вопрос вызвал замешательство… Действительно, они не обращали на это внимание раньше. Вы, мои дорогие читатели, уже наверняка догадались в чем подвох. Конечно же в тренажере был подвижный ролик, тот самый блок, который катался вверх-вниз, удерживываемый тросиком, и давал выигрыш в силе в 2 раза. То есть по факту человек поднимает в этом тренажере 35 кг, а не 70 кг, как написано на плитках. Многие об этом не задумываются 🙂
Подвижный блок можно считать воистину крутым изобретением человечества. Ведь он дает возможность поднять груз, который мы бы никогда не подняли своими силами без этого хитрого приспособления.
Но во всём ли мы выигрываем? Нет, не во всём. Как и любой рычаг, подвижный блок помогает выиграть в силе, но проиграть в расстоянии. Это можно понять, если считать, что работа, выполняемая нами по мерещению груза (изменению его потенциальной энергии в случае подъема) является величиной постоянной ( *здесь мы пока не учитываем трение, которое есть в любых блоках, подшипниках и других механизмах ).
Как видите по рисункам, выиграть можно и в 4 раза, используя только два блока. Такая конструкция часто применяется в подъемных кранах. Однако, чем тяжелее груз, тем медленнее его будут поднимать. Такой же принцип наблюдается в коробке передач автомобиля, такой же принцип работает в переключении скоростей велосипеда. Чем быстрее, тем труднее. Или наоборот, чем легче, тем медленее.
Случай 4
Что если мы усложним наш пример, включив в него ускорение? Здесь важно не забыть учесть тот момент, который мы уже обсуждали в предыдущем пункте. Ускорение центра масс подвижного блока будет в два раза меньше, чем ускорение свободного конца длинной нити, протянутой через два блока. Почему? Попытаюсь это продемонстрировать на рисунке ниже.
Определить соотношение сил и перемещений можно с помощью метода виртуальных перещений. Однажды во время строительства одного из соборов в Швейцарии его архитектору понадобились блоки, позволяющие поднимать на большую высоту особо тяжелые грузы. Он сконструировал сложный полиспаст ( это грузоподъемное устройство, которое натягивается несколькими тросами. подробнее ), но запутался в многочисленных силах натяжения тросов и не смог рассчитать, сколько рабочих будет нужно нанимать для обслуживания грузоподъемного устройства. Архитектор обратился за помощью к известному ученому того времени Иоганну Бернулли (1667 – 1748). Едва взглянув на чертеж, Бернулли сразу же дал ответ. Разумеется, архитектор был очень удивлен и попросил объяснить ему суть решения…
Часто в задаче нужно учесть условия равновесия системы. Для этого определяются силы реакций механических связей. Связи — это ограничения, наложенные на положение отдельных частей системы или их возможные перемещения. Связями могут быть нити, шарниры, блоки. Чем больше связей, тем сложнее проследить за возникающими в них реакциями.
В большинстве случаев мехнические связи обладают интересным свойством, которое Бернулли положил в основу своего простого и изящного способа нахождения условий равновесия механической системы. Напишем это свойство:
Полная работа всех сил реакции, возникающих в связях системы при любых достаточно малых возможных отклонениях системы от положения равновесия, равна нулю.
Замечание: любые возможные отклонения не должны противоречить механическим связям: нити не должны рваться, шарниры не должны ломаться, блоки не должны деформироваться. Это и есть возможные или виртуальные перемещения.
Бернулли сформулировал этот принцип в 1717 году. Получается, что для исследования равновесия системы, достаточно выбрать удобные виртуальные перемещения (мы рисовали это выше), вычислить соответствующую им работу только внешних сил, а затем приравнять её к нулю.
Хотите простейший пример на применение данного метода? Давайте представим, что некоторый груз массой m подвешивают на пружину, и он её растягивает с силой тяжести m•g. При этом в самой пружине возникает сила упругости T. Допустим, груз сместился вниз на маленькую величину Δx. Тогда работа силы тяжести будет равна ΔA₁ = m•g•Δx, а работа силы упругости пружины будет ΔA₂ = − T•Δx. Знак минус здесь стоит потому что сила упругости всегда направлена против перемещения (вспоминайте закон Гука). Тогда, согласно принципу возможных перемещений, сумма работ обеих сил должна быть равна нулю:
ΔA₁ + ΔA₂ = m•g•Δx − T•Δx = 0 откуда получаем T = m•g
Замечание: Конечно же эту задачу можно решить обычным способом. Более того, оба метода будут примерно одинаковы по степени сложности. НО, существуют случаи, когда применение метода возможных перемещений дает более быстрое и простое решение. Иногда позволяет решать задачи, которые не разрешаются на основе обычнх уловий равновесия. Этот метод можно применяться не только для задач механики, но и для задач электростатики или молекулярной физики.
Итак, ускорение повлияет на силы, но не сильно. Мы же помним, что в нашем случае блоки по-прежнему идеальные, то есть их массу мы принимает за ноль (соответственно, момент инерции тоже).
Вот на этом моменте уже хочется обозначить несколько общих принципов решения таких задач.
Алгоритм, общие принципы, замечания
1. При решении нужно выяснить, какие силы действуют на тело, движение которого мы рассматриваем в конкретный момент времени. Все известные силы надо изобразить, сделать рисунок. Понимать со стороны каких тел действуют рассматриваемые силы. Действие одного тело на другое является взаимным (третий закон Ньютона). Бывает такое, что направление силы заранее неизвестно. Здесь не стоит переживать. Выберите то направление, которое вам кажется верным. При проецировании второгой закона Ньютона вы сможете получить численные значения для проекций. И если они будут положительные, то вы угадали с направлением. А если будут отрицательные, то вы не угадали, значит рисунок нужно подкорректировать, инвертировал стрелку, обозначающую силу. Если в задаче рассматривается несколько тел, то разумеется нужно расставить силы, действующие на все тела.
2. Далее осуществляется выбор системы отсчета. Оси (базис XOY) нужно выбирать так, что проекции был как можно более простыми, то есть чтобы как можно большее количество сил были параллельны или перпендикулярны выбранным осям.
3. Для каждого тела в системе записывается второй закон Ньютона. Затем этот закон проецируется на оси выбранного базиса (см 2 пункт). По началу вы можете сразу подставлять в полученную систему уравнений известные вам силы, углы, массы и проекции сил. Однако хорошим тоном является доведения решения до конца в буквенном виде. Если вы сейчас учитесь в школе, то обязательно научитесь оперировать буквами без подстановки чисел.
4. Для решения задач о движении системы тел одних уравнений движения (проекций второго закона Ньютона) может быть недостаточно. Нужна записать ещё все кинематические условия. Эти условия определяют соотношения между ускорениями различных объектов системы, обусловленные связями между ними.
Пример для неподвижных блоков: тела, связанные нерастяжимой нитью (идеальная нить), имеют вдоль этой нити одинаковые по модулю ускорения. И не важно через сколько неподвижных блоков перекинута нить.
Пример для подвижных блоков: При наличии подвижных блоков, ускорение тела (или свободного конца нити), перекинутой через неподвижный блок в два раза больше ускорения тела, прикрепленного к подвижному блоку. Так как за одинаковое время пройденные пути отличаются в два раза (мы это разбирали выше в статье).
5. Во множестве простых задач теоретической механики массой нитей, связывающих тела, пренебрегают. Только тогда натяжение таких нитей одинаково, какое бы мы не взяли сечение на всей длине.
6. Массой блоков также пренебрегают во множестве задач. В этих случаях натяжение нити, перекинутой через такой идеальный блок, можно считать одинаковым по обе стороны блока. В противном случае, если учитывать массу, то натяжения будут разными, угловая скорость будет меняться, то есть у нас появится вращающий момент сил, угловое ускорение и момент инерции реального блока.
7. Очень полезно попытаться понять как будут изменяться искомые величины при изменениях заданных величин. Если вы построите графики таких зависимостей, то сможете лучше разобраться в задаче.
Случай 5
Давайте рассмотрим задачу, в которой мы имеем два разных груза и два разных блока (подвижный и неподвижный.
Задача
Найдите силы натяжения T₁ и T₂ нитей abcd и ce в устройстве с подвижным блоком, изображенном на рисунке. Массы тел соответственно равны m₁ = 2 кг и m₂ = 3 кг.
Решение:
Обратите внимание, что сила натяжения оранжевой длинной веревки abcd меньше, чем сила натяжения короткой желтой веревки ce, хотя на короткой веревке груз висит более легкий, чем на длинной веревке. Получается, что сила натяжения уменьшается при постоянном движении троса.
Случай 6
В задачах на блоки грузы необязательно могут быть подвешены. Бывает так, что грузы скользят по плоскостям, потому как блок опускается под действием силы тяжести груза, прикрепленного к нему. Рассмотрим такой случай.
Задача
На рисунке изображена система движущихся тел, имеющих массы m₁ = m, m₂ = 4m, m₃ = m. Наклонная плоскость составляет с горизонтом угол α = 30°. Трение отсутствует. Определите силы натяжения нитей.
Решение:
Случай 7
Встречаются и более редкие задачи, которые вводят учащихся в замешательство. Это задачи связанные с реальными блоками. Основное отличие заключается в том, что мы учитываем массу блока, а следовательно учитываем его момент инерции. Для раскрутки блока с массой (реального блока) нужен ненулевой момент сил (в сторону вращения). Значит такие задачи отличаются тем, что силы натяжения одной и той же нити на таком блоке будут разные по обе стороны от перегиба нити на блоке. Звучит сложно? Понимаю… Сейчас мы разберемся как это работает на практике.
При описании движения по окружности (другими словами при описании вращения тела) удобно использовать величины угла поворота φ, угловой скорости ω, углового ускорения ε и момента сил M.
Роль массы при вращении тела (или движении по окружности) играет величина J = m·R². Будем называть эту величину моментом инерции. Тогда уравнение вращательного движения по окружности для точки можно записать в виде: J·ε = M. По своей сути последнее уравнение является удобной записью второго закона Ньютона в проекциях на тангенциальное (касатальное) направление при движении по окружности.
Момент инерции является мерой инертности тела. К примеру, камень на длинной верёвке будет раскрутить сложнее, чем на короткой.
Вопрос читателям канала: Почему велосипедной колесо до одной и той же угловой скорости легче раскрутить пацльцем, если прикладывать силу к ободу колеса, чем если прикладывать силу к спицам возле втулки?
Блоки из наших задач выше не являются материальными точками. Поэтому момент инерции для них выводится с помощью суммирования моментов инерции всех частичек (материальных точек), из которых состоит блок.
Наш блок мы будем представлять в виде сплошного диска, сделанного из однородного материала. Момент инерции такого блока J = 1/2·m·R². Возможно, вам непонятно откуда взялась 1/2 ? Тогда выведем формулу…
Вывод формулы для момента инерции кольца и диска (блока) при вращении вокруг оси, проходящей через центр симметрии диска (блока):
Задача с реальным блоком
Через блок, представляющий собой сплошной диск радиусом R, перекинута нить. На нити подвешены грузы массами m₁ и m₂ ( m₂ > m₁). Масса блока m. Определите разность сил натяжения нитей с обеих сторон блока и ускорение грузов. Считать, что нить нерастяжима и не может скользить по блоку.
Решение:
Как видно из решения, больше натягивается та часть нити, в сторону которой происходит вращение блока, то есть та часть, которая разматывает блок. Именно она и может порваться, ведь натяжение в ней больше. Обратим внимание, что разница натяжений в частях нити пропорциальна ускорение грузов и массе блока.
В этой статье разобрано 7 основных случаев, из которых состоят задачи на блоки. И я очень надеюсь, что вам было интересно почитать эту статью. Ибо время на неё было потрачено очень много.
💾 Метод виртуальных перемещений (скачать полезные задачи в pdf)
Ладно, пора заканчивать эту бесконечную статью… А то, боюсь, что до этого момента уже никто не дочитает. Тяжело читать статьи, в которых много математики. Есть и более приятный контент для расслабления.
📚 На Дзен недавно появился интересный канал «Читающий Лингвист». Автор канала пишет замечательные рецензии на зарубежную литературу, рассказывает о прочитанном и делает заметки на околокнижные лингвистические наблюдения.
Советую подписаться на этот авторский канал «Читающего Лингвиста»
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Подвижный блок отличается от неподвижного тем, что его ось не закреплена, и он может подниматься и опускаться вместе с грузом.
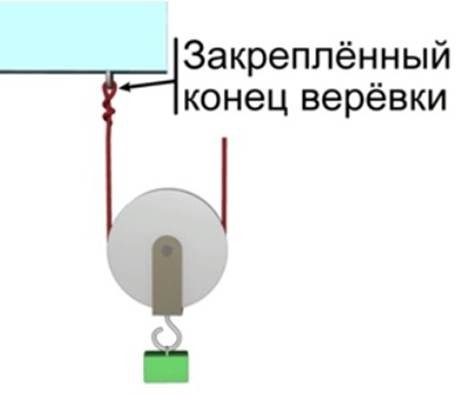
Рисунок 1. Подвижный блок
Как и неподвижный блок, подвижный блок состоит всё из того же колеса с желобом для троса. Однако здесь закреплен один конец троса, а колесо подвижно. Колесо движется вместе с грузом.
Как заметил ещё Архимед, подвижный блок по сути является рычагом и работает по тому же принципу, давая выигрыш в силе за счёт разницы плеч.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
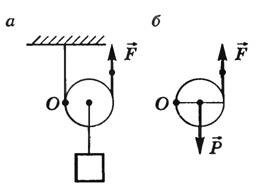
Рисунок 2. Силы и плечи сил в подвижном блоке
Подвижный блок перемещается вместе с грузом, он как бы лежит на веревке. В таком случае точка опоры в каждый момент времени будет находиться в месте соприкосновения блока с веревкой с одной стороны, воздействие груза будет приложено к центру блока, где он и крепится на оси, а сила тяги будет приложена в месте соприкосновения с веревкой с другой стороны блока. То есть плечом веса тела будет радиус блока, а плечом силы нашей тяги — диаметр. Правило моментов в этом случае будет иметь вид:
$$mgr = F cdot 2r Rightarrow F = mg/2$$
Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 3). Неподвижный блок применяется только для удобства. Он, изменяет направление действия силы, позволяет, например, поднимать груз, стоя на земле, а подвижный блок обеспечивает выигрыш в силе.
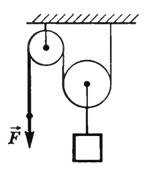
Рисунок 3. Комбинация неподвижного и подвижного блоков
Мы рассмотрели идеальные блоки, то есть такие, в которых не учитывалось действие сил трения. Для реальных же блоков необходимо вводить поправочные коэффициенты. Используют такие формулы:
Неподвижный блок
$F = f • mg $
Подвижный блок
$F = f • 1/2 mg $
В этих формулах: $F$ – прилагаемое внешнее усилие (обычно это сила рук человека), $m$ – масса груза, $g$ – коэффициент силы тяжести, $f$ – коэффициент сопротивления в блоке (для цепей примерно 1,05, а для верёвок 1,1).
«Подвижный блок» 👇
Задача 1
С помощью системы из подвижного и неподвижного блоков грузчик поднимает ящик с инструментами на высоту $S_1$ = 7 м, прикладывая силу $F$ = 160 Н. Какова масса ящика, и сколько метров верёвки придётся выбрать, пока груз поднимется? Какую работу выполнит в результате грузчик? Сравните её с работой, выполненной над грузом по его перемещению. Трением и массой подвижного блока пренебречь.
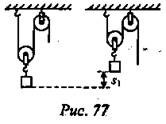
Решение
Дано:
$F$ = 160 H
$S_1$ = 7 м
$m, S_2 , A_1 , A_2$ – ?
Подвижный блок даёт двойной выигрыш в силе и двойной проигрыш в перемещении. Неподвижный блок не даёт выигрыша в силе, но меняет её направление. Таким образом, приложенная сила будет вдвое меньше веса груза: $F = 1/2P = 1/2mg$, откуда находим массу ящика: $m=frac{2F}{g}=frac{2cdot 160}{9,8}=32,65 кг$
Перемещение груза будет вдвое меньше, чем длина выбранной верёвки:
[S_2=2S_1=2cdot 7=14 м]
Выполненная грузчиком работа равна произведению приложенного усилия на перемещение груза: $A_2=Fcdot S_2=160cdot 14=2240 Дж $.
Работа, выполненная над грузом:
[A_1=mgS_1=32,65cdot 9,8cdot 7=2240 Дж]
Ответ: Масса ящика 32,65 кГ. Длина выбранной верёвки 14 м. Выполненная работа равна 2240 Дж и не зависит от способа подъёма груза, а только от массы груза и высоты подъёма.
Задача 2
Какой груз можно поднять с помощью подвижного блока весом 20 Н, если тянуть веревку с силой 154 Н?
Решение
Дано:
$Р_Б$ = 20 Н
$F$ = 154 H
$f$ = 1,1
$P$ – ?
Запишем правило моментов для подвижного блока: $F = f • 1/2 (P+ Р_Б)$, где $f$ – поправочный коэффициент для верёвки.
Тогда $P=2frac{F}{f}-P_Б=2cdot frac{154}{1,1}-20=260 Н$
Ответ: Вес груза 260 Н.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
losin500
Вопрос по физике:
Вычислите массу груза, который можно поднять с помощью подвижного блока, если к свободному веревки прикладывается сила 100Н. Масса самого блока 500 г.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ldremoumat
выигрыш в силе на подвижном блоке 2 раза
сила F=100 Н
общий вес P = 2F=200 Н
общая масса M=P/g=200/10= 20 кг
масса груза Мг = М- Мб= 20 – 0.5= 19.5 кг
ОТВЕТ 19.5 кг
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

Вычислите массу груза которой можно поднять с помощью подвижного блока если к свободному концу верёвки прикладывается сила 100н Масса самого блока 500г
Ответ:19,5 кг
НАДО РЕШЕНИЕ!
Светило науки – 539 ответов – 12802 помощи
Подвижный блок дает выигрыш в силе в два раза. То есть если приложили силу 100Н, значит на противоположность конце совершается сила 100•2=200Н
Теперь найдем массу груза
Мгруза=m1-м2=200:10-0,5кг=20-0,5=19,5кг. Если что непонятно, обращайся в лс

Светило науки – 93 ответа – 2239 раз оказано помощи
так как подвижный блок даёт выиграш в силе в 2 раза, то 100Н*2 = 200Н
Си: 500г = 0.5 кг
Масса груза = Масса1 – масса2
масса1 = Р/g = 200H / 10Нкг = 20 кг
Масса груза = 20кг – 0.5 кг = 19.5 кг
Ответ : 19.5 кг – масса груза
