Как найти массу капли масла

На этой странице находится вопрос Между горизонтальными заряженными пластинами находятся в покое капелька масла, заряд которой q – = 1, 6 * 10 – 16 кл?, относящийся к категории
Физика. По уровню сложности данный вопрос соответствует знаниям
учащихся 10 – 11 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Физика. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Содержание

• Объяснение эксперимента
• Масса масляной капли
• Важность
• Капли с множеством зарядов
• пример
• Поднимая каплю масла
• Решение для
• Решение б
• Решение c
• Ссылки

В Милликан эксперимент, проведенная Робертом Милликеном (1868-1953) вместе со своим учеником Харви Флетчером (1884-1981), началась в 1906 году и была направлена ​​на изучение свойств электрического заряда, анализируя движение тысяч капель масла между ними. однородного электрического поля.

Был сделан вывод, что электрический заряд не имел произвольного значения, а был кратен 1,6 x 10.^-19 C, который является основным зарядом электрона. Кроме того, была найдена масса электрона.

Ранее физик Дж. Дж. Томпсон экспериментально обнаружил отношение заряда к массе этой элементарной частицы, которую он назвал «корпускулой», но не значения каждой величины в отдельности.

Из этого соотношения заряд-масса и заряда электрона было определено значение его массы: 9,11 x 10^-31 Кг.

Для достижения своей цели Милликен и Флетчер использовали распылитель, который распылял мелкий туман из капель масла. Некоторые капли были электрически заряжены из-за трения в распылителе.

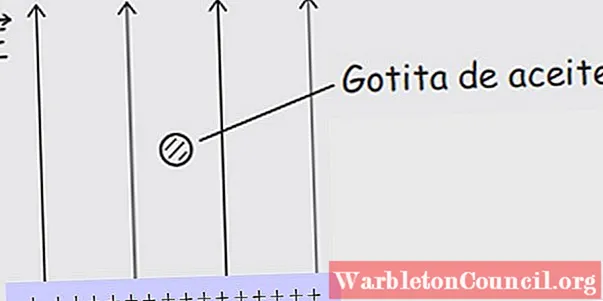
Заряженные капли медленно оседали на параллельных плоских пластинчатых электродах, некоторые из которых проходили через небольшое отверстие в верхней пластине, как показано на схеме на рисунке 1.

Внутри параллельных пластин можно создать однородное электрическое поле, перпендикулярное пластинам, величина и полярность которого контролировались изменением напряжения.

За поведением капель наблюдали, освещая внутреннюю часть пластин ярким светом.

Объяснение эксперимента

Если капля имеет заряд, поле, созданное между пластинами, оказывает на нее силу, противодействующую гравитации.

И если ему также удается оставаться в подвешенном состоянии, это означает, что поле оказывает восходящую вертикальную силу, которая точно уравновешивает гравитацию. Это условие будет зависеть от значения какие, бремя капли.

Действительно, Милликен заметил, что после включения поля некоторые капли приостановились, другие начали подниматься или продолжали опускаться.

Регулируя величину электрического поля – например, с помощью переменного сопротивления – можно было заставить каплю оставаться в подвешенном состоянии внутри пластин. Хотя на практике добиться этого непросто, если это произойдет, на каплю действуют только сила поля и гравитации.

Если масса капли равна м и его нагрузка какие, зная, что сила пропорциональна приложенному полю величины А ТАКЖЕ, Второй закон Ньютона гласит, что обе силы должны быть сбалансированы:

мг = q.E

q = мг / Э

Значение грамм, ускорение свободного падения известно, а также величина А ТАКЖЕ поля, которое зависит от напряжения V устанавливается между пластинами и зазор между ними L, в качестве:

E = V / L

Вопрос состоял в том, чтобы найти массу крошечной капли масла. Как только это будет выполнено, определите нагрузку какие это вполне возможно. Естественно, что м Y какие они представляют собой соответственно массу и заряд масляной капли, а не электрона.

Но … капля заряжена, потому что она теряет или приобретает электроны, поэтому ее величина связана с зарядом указанной частицы.

Масса масляной капли

Задача Милликена и Флетчера заключалась в том, чтобы определить массу капли, что было непростой задачей из-за ее небольшого размера.

Зная плотность масла, если у вас есть объем капли, можно решить массу. Но и объем был очень мал, поэтому обычные методы были бесполезны.

Однако исследователи знали, что такие маленькие объекты не падают свободно, поскольку сопротивление воздуха или окружающей среды вмешивается, замедляя их движение. Хотя частица, выпущенная с отключенным полем, испытывает ускоренное вертикальное движение вниз, в конечном итоге она падает с постоянной скоростью.

Эта скорость называется «конечной скоростью» или «предельной скоростью», которая в случае шара зависит от его радиуса и вязкости воздуха.

В отсутствие поля Милликен и Флетчер измерили время, за которое капли упали. Предполагая, что капли были сферическими и с учетом вязкости воздуха, им удалось определить радиус косвенно из конечной скорости.

Эта скорость находится путем применения закона Стокса, и вот его уравнение:

–v_т конечная скорость

–р – радиус капли (сферической)

–η вязкость воздуха

–ρ это плотность капли

Важность

Эксперимент Милликена имел решающее значение, потому что он выявил несколько ключевых аспектов физики:

I) Элементный заряд – это заряд электрона, значение которого составляет 1,6 x 10 ^-19 C, одна из фундаментальных констант науки.

II) Любой другой электрический заряд кратен фундаментальному заряду.

III) Зная заряд электрона и соотношение заряда и массы Дж. Дж. Томсону удалось определить массу электрона.

III) На уровне таких мелких частиц, как элементарные частицы, гравитационные эффекты незначительны по сравнению с электростатическими.

За эти открытия Милликен получил Нобелевскую премию по физике в 1923 году. Его эксперимент важен еще и потому, что он определил эти фундаментальные свойства электрического заряда, начав с простой аппаратуры и применив хорошо известные всем законы.

Однако Милликена критиковали за то, что он отказался от многих наблюдений в своем эксперименте без видимой причины, чтобы уменьшить статистическую ошибку результатов и сделать их более «презентабельными».

Капли с множеством зарядов

Милликен измерил очень много капель в своем эксперименте, и не все из них были маслом. Он также пробовал ртуть и глицерин. Как уже говорилось, эксперимент начался в 1906 году и длился несколько лет. Три года спустя, в 1909 году, были опубликованы первые результаты.

За это время он получил множество заряженных капель, пропуская рентгеновские лучи через пластины, чтобы ионизировать воздух между ними. Таким образом высвобождаются заряженные частицы, которые могут принять капли.

Кроме того, он не сосредоточился исключительно на взвешенных каплях. Милликен заметил, что, когда капли поднимаются, скорость подъема также варьируется в зависимости от доставляемой нагрузки.

И если капля опустилась, этот дополнительный заряд, добавленный благодаря вмешательству рентгеновских лучей, не изменил скорость, потому что любая масса электронов, добавленных к капле, мизерна по сравнению с массой самой капли.

Независимо от того, сколько заряда он добавил, Милликен обнаружил, что все капли приобрели заряды, целые кратные определенной величине, которая равна а также, фундаментальная единица, которая, как мы уже сказали, является зарядом электрона.

Милликен изначально набрал 1592 х 10^-19 C для этого значения, немного меньше принятого в настоящее время, которое составляет 1602 x 10^-19 C. Причиной могло быть значение, которое вы указали для вязкости воздуха в уравнении для определения конечной скорости капли.

пример

Поднимая каплю масла

Мы видим следующий пример. Капля нефти имеет плотность ρ = 927 кг / м3.³ и выпускается в середине электродов при выключенном электрическом поле. Капля быстро достигает предельной скорости, по которой определяется радиус, значение которого оказывается R = 4,37 × 10^-7 м.

Равномерное поле включается, направлено вертикально вверх и имеет величину 9,66 кН / С. Таким образом достигается то, что капля остается приостановленной в состоянии покоя.

Спрашивает:

а) Рассчитайте заряд капли

б) Найдите, сколько раз элементарный заряд содержится в заряде капли.

c) Определите, если возможно, знак нагрузки.

Решение для

Ранее для капли в состоянии покоя было получено следующее выражение:

q = мг / Э

Зная плотность и радиус капли, определяется масса капли:

ρ = м / В

V = (4/3) πR³

Таким образом:

м = ρ.V = ρ. (4/3) πR³= 927 кг / м³. (4/3)π.(4,37 х 10^-7 м)³= 3,24 х 10^-16 кг

Следовательно, заряд капли равен:

д = мг / Е = 3,24 х 10^-16 кг x 9,8 м / с²/ 9660 Н = 3,3 х 10^-19 C

Решение б

Зная, что основной заряд равен e = 1,6 x 10 ^-19 C нагрузка, полученная в предыдущем разделе, делится на это значение:

п = д / е = 3,3 х 10^-19 C /1,6 х 10 ^-19 С = 2,05

В результате заряд капли примерно в два раза (n≈2) больше заряда элемента. Это не совсем двойное значение, но это небольшое несоответствие связано с неизбежным присутствием экспериментальной ошибки, а также округлением в каждом из предыдущих расчетов.

Решение c

Определить знак заряда возможно, благодаря тому, что в выписке даются сведения о направлении поля, которое направлено вертикально вверх, а также о силе.

Линии электрического поля всегда начинаются положительными зарядами и заканчиваются отрицательными зарядами, поэтому нижняя пластина заряжена знаком +, а верхняя – знаком – (см. Рисунок 3).

Поскольку капля направлена ​​к пластине вверху под действием поля и поскольку заряды противоположного знака притягиваются друг к другу, капля должна иметь положительный заряд.

На самом деле, удержать каплю в подвешенном состоянии непросто. Таким образом, Милликен использовал вертикальные смещения (взлеты и падения), которые испытывала капля при включении и выключении поля, а также изменения в заряде рентгеновского излучения и времени пробега, чтобы оценить, сколько дополнительного заряда приобрела капля.

Этот приобретенный заряд пропорционален заряду электрона, как мы уже видели, и может быть рассчитан с учетом времени нарастания и спада, массы капли и значений грамм Y А ТАКЖЕ.

Ссылки

1. Открытый разум. Милликен, физик, который пришел посмотреть на электрон. Получено с: bbvaopenmind.com
2. Рекс, А. 2011. Основы физики. Пирсон.
3. Типпенс, П. 2011. Физика: концепции и приложения. 7-е издание. Макгроу Хилл.
4. Амрита. Эксперимент Милликена с каплей масла. Получено с: vlab.amrita.edu
5. Колледж Уэйк Форест. Капля масла Милликена Эксперимент. Получено с: wfu.edu

Напишите мини-сочинение на тему школьных дней (на английском), по плану вступление,преимущества(школы),недостатки(школы),итог. Используя данные выражения: Some of the advantages:

to become smarter, to develop your mind, to take part in school activities, to have good sports facilities, to have good and experienced teachers, to have interesting school traditions, to develop your imagination, to study interesting subjects, to learn new things, to prepare for adult life, to have a lot of friends, to enjoy school life and friendship…

Some of the disadvantages:

not to need so much knowledge, to have no time for sports and hobbies, to get up early in the morning every day, to be tired of doing homework, to work too hard, not to be allowed to do what you want to, to have boring lessons, to be afraid of some teachers, to have too many extra subjects, to worry about getting good marks, to have many tests, school has nothing to do with real life…

Лабораторная работа № 5

Тема: «ИЗМЕРЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ»

Цель: определить коэффициент поверхностного натяжения воды методом отрыва капель.

Оборудование: сосуд с водой, шприц, сосуд для сбора капель.

Теория.

   Молекулы поверхностного слоя жидкости обладают избытком потенциальной энергии по сравнению с энергией молекул, находящихся внутри жидкости

   Как и любая механическая система, поверхностный слой жидкости стремится уменьшить потенциальную энергию и сокращается. При этом совершается работа А:

   где σ – коэффициент поверхностного натяжения. Единицы измерения Дж/м² или Н/м

или  

   где F – сила поверхностного натяжения, l – длина границы поверхностного слоя жидкости.

   Поверхностное натяжение можно определять различными методами. В лабораторной работе используется метод отрыва капель.

   Опыт осуществляют со шприцом, в котором находится исследуемая жидкость. Нажимают на поршень шприца так, чтобы из отверстия узкого конца шприца медленно падали капли. Перед моментом отрыва капли сила тяжести F_тяж=m_капли·g равна силе поверхностного натяжения F, граница свободной поверхности – окружность капли

l=π·d_капли

   Следовательно:

   Опыт показывает, что d_капли =0,9d, где d – диаметр канала узкого конца шприца.

   Массу капли можно найти, посчитав количество капель n и зная массу всех капель m.

   Масса капель m будет равна массе жидкости в шприце. Зная объем жидкости в шприце V и плотность жидкости ρ можно найти массуm=ρ·V

Ход работы.

   1. Подготовьте оборудование:
   Начертите таблицу:

№ опыта	Масса капель m, кг	Число капель n	Диаметр канала шприца d, м	Поверхност-ное натяжение σ, Н/м	Среднее значение поверхностного натяжения σср, Н/м	Табличное значение поверхност-ного натяжения σтаб, Н/м	Относительная погрешность δ %
1	1*10-3		2,5*10-3			0,072
2	2*10-3		2,5*10-3
3	3*10-3		2,5*10-3

Опыт 1

1. Наберите в шприц 1 мл воды («один кубик»).
2. Подставьте под шприц сосуд для сбора воды и, плавно нажимая на поршень шприца, добейтесь медленного отрывания капель. Подсчитайте количество капель в 1 мл и результат запишите в таблицу.

1. Вычислите поверхностное натяжение по формуле 

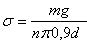
Результат запишите в таблицу.

1. Повторите опыт с 2 мл и 3 мл воды.
2. Найдите среднее значение поверхностного натяжения 

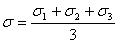
Результат запишите в таблицу.

1. Сравните полученный результат с табличным значением поверхностного натяжения с учетом температуры.
2. Определите относительную погрешность методом оценки результатов измерений.

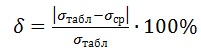
   Результат запишите в таблицу.

1. Сделайте вывод.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Почему поверхностное натяжение зависит от рода жидкости?
2. Почему и как зависит поверхностное натяжение от температуры?
3. Изменится ли результат вычисления поверхностного натяжения, если опыт проводить в другом месте Земли?
4. Изменится ли результат вычисления, если диаметр капель трубки будет меньше?
5. Почему следует добиваться медленного падения капель?

Вариант выполнения лабораторной работы.

Результаты измерений:

Количество капель в 1 мл – 21

Количество капель в 2 мл – 40

Количество капель в 3 мл – 59