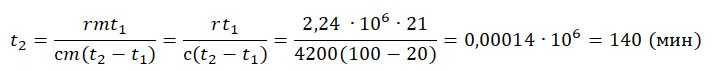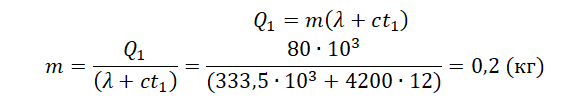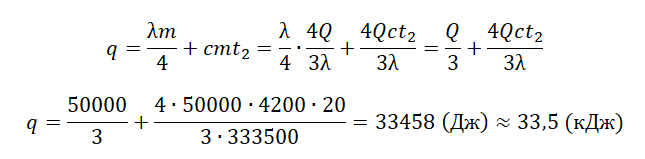Светило науки – 9969 ответов – 46531 помощь
Дано:
– лёд массой 3 кг при -10°,
– вода массой 0,5 кг при +10°.
Табличные данные:
удельная теплоемкость воды меняется вместе с изменением ее температуры в кДж/кг:
при температуре льда в минус десять – 2,22;
при температуре льда в ноль градусов – 2,11;
при нуле градусов в жидком состоянии – 4,218;
при температуре плюс десять градусов – 4,192;
удельная теплота плавления при температуре ноль градусов по Цельсию — 333,55.
Примем средние значения теплоёмкости:
– вода
4205 Дж/кг*градус,
– лёд 2165 Дж/кг*градус.
Вода, остывая от 10 до 0 градусов, выделит 0,5*4205*10 =
21025 Дж.
Лёд при этом нагреется на
21025/(3*2165) =
3,237105 градуса и будет иметь температуру -10 +
3,237105 = –
6,762895 градуса.
От более тёплой воды он будет отнимать тепло, превращая её в лёд.
Его образуется (6,762895*3*2165)/333550 = 0,131689 кг.
Ответ:
Итого льда
3,131689
кг
и
0,368311
воды
при 0 градусов.
В
алюминиевом колориметре массой 250 г находятся вода массой 1,2 кг при
температуре 250 C. В колориметр положили
лед, имеющий температуру -100 C.
Определите массу льда, если после установления теплового равновесия температура
воды оказалась равной 50 C. Удельные теплоемкости
льда 2,1 кДж/(кг•K), воды 4,2 кДж/(кг•K), алюминия 920 Дж/(кг•K); удельная теплота плавления льда 0,33 МДж/кг.
Решение.
При
установлении теплового равновесия в рассматриваемой среде происходят следующие
процессы, сопровождаемые выделением или поглощением теплоты:
•
охлаждение воды, Q1 = m1cв(q – t1);
•
охлаждение колориметра, Q2 = maca(q – t1);
•
нагревание льда, Q3 = m2cл(0 – t2);
•
плавление льда, Q4 = m2l;
•
нагревание воды, получаемой при таянии льда, Q5 = m2cв(q – 0).
Считая
систему замкнутой, в которой не совершается работа, можно составить уравнение
теплового баланса.
Отсюда
находим m2
.
Ответ:
m2 = 0.28 кг.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
В калориметр, в котором находилась вода массой 2 кг при температуре 0 °C, бросили 500 г льда при температуре −66 °C. Какая масса льда в граммах окажется в калориметре после установления теплового равновесия? (Удельная теплоёмкость льда — 2100 Дж/(кг · °С), удельная теплота плавления льда — 3,3 · 105 Дж/кг.)
Спрятать решение
Решение.
Найдём количество теплоты, которое необходимо затратить, чтобы нагреть лёд до 0 °C
Это количество теплоты будет образовано за счёт замерзания воды. В лёд превратится часть воды массой
Таким образом, после установления теплового равновесия в калориметре окажется 500 + 210 = 710 г льда.
Ответ: 710.
Предмет: Физика,
автор: kurolovgiyas
Ответы
Автор ответа: alexlar30
0
Ответ:
1,1 кл льда
Объяснение:
Для решения применяем условие теплового баланса.
См. фото.
Приложения:


Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Английский язык,
автор: Анастасия124
помогите составить рассказ на тему “как я поддерживаю свою форму”. плиз очень надо:* (7 предложений.. о спорте и о пище уже написано)
1 месяц назад
Предмет: Геометрия,
автор: Аноним
о-центр окружности В-точка касания Найти:угол АВD
1 месяц назад
Предмет: Математика,
автор: Помогитепапе
Как правильно записать условие к заданию.
Из коробки взяли 6 кубиков. Сколько кубиков надо положить в коробку, чтобы в ней стало на 3 кубика больше чем было.
(решение понятно 6+3=9)подскажите как записать и оформить задачу для первого класса
1 месяц назад
Предмет: Математика,
автор: bemakkkk
При каких натуральных значенияхm дробь (m+4)/2m неправильная? Запишите эти дроби
КТО СДЕЛАЕТ ТОМУ 20 б !!!!!
6 лет назад
Предмет: Математика,
автор: bmonolova1980
У саши 9 карандашей ,что в 3 раза больше,чем у лены.сколько карандашей у них вместе?
6 лет назад
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
ОпределениеПлавление — переход вещества из твердого состояния в жидкое.
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
Q=λm
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
ОпределениеОтвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Q=−λm
Парообразование и конденсация
ОпределениеПарообразование, или кипение — переход вещества из жидкого состояния в газообразное.
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
Q=rm
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
ОпределениеКонденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Q=−rm
Тепловые процессы при нагревании и охлаждении
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела |
Q=cтm(tпл−t0) ст — удельная теплоемкость вещества в твердом состоянии. |
| 2–3 | Плавление при температуре плавления (tпл) |
Q=λm |
| 3–4 | Нагревание жидкости |
Q=cжm(tкип−tпл) сж — удельная теплоемкость вещества в жидком состоянии. |
| 4–5 | Кипение при температуре кипения (tкип) |
Q=rm |
| 5–6 | Нагревание пара |
Q=cпm(t−tкип) сп — удельная теплоемкость вещества в газообразном состоянии. |
| 6–7 | Охлаждение пара |
Q=cпm(tкип−t) |
| 7–8 | Кипение при температуре кипения (tкип) |
Q=−rm |
| 8–9 | Охлаждение жидкости |
Q=cжm(tпд−tкип) |
| 9–10 | Отвердевание при температуре плавления (tпл) |
Q=−λm |
| 10–11 | Охлаждение твердого тела |
Q=cтm(t0−tпл) |
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 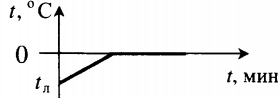 |
Q=cлm(tпл−tл)+λm cл — удельная теплоемкость льда, tл — начальная температура льда. |
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 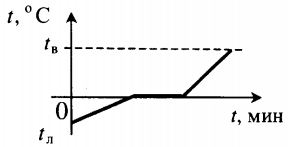 |
Q=cлm(tпл−tл)+λm+cвm(tв−tпл) cв — удельная теплоемкость воды. |
| Взяли лед при температуре 0 оС и полностью испарили. | 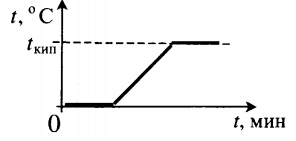 |
Q=λm+cвm(tкип−tпл)+rm |
| Взяли воду при комнатной температуре и половину превратили в пар. | 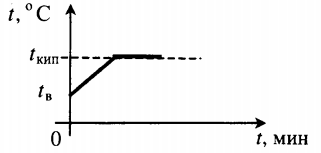 |
Q=cвm(tкип−tв)+rm2 |
Подсказки к задачам
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 оС. |
| Объем воды 5 л | m = 5 кг, так как:
m=ρV=103· Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 оС, чтобы превратить его в воду и нагреть ее до температуры +30 оС?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q=Q1+Q2+Q3
Q=cлm(0−t1)+λm+cвm(t2−0)
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙103 Дж/кг.
Отсюда:
Q=2050·2(0−(−10))+333,5·103·2+4220·2·30=961200 (дж)=961,2 (кДж)
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Qотд=−Qпол
Отданное количество теплоты меньше нуля (Qотд < 0), а полученное количество теплоты положительно (Qполуч > 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 оС. Учтите, что лед плавится, если он находится при температуре 0 оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 оС, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 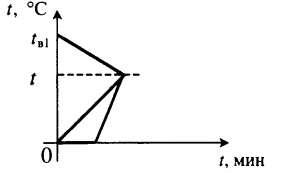
Уравнение теплового баланса: Q1+Q2+Q3=0 cвmв1(t−tв1)+cвmв2(t−0)+λmл+cвmл(t−0)=0 |
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 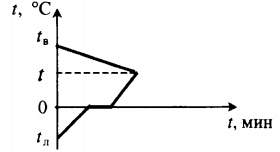
Уравнение теплового баланса: Q1+Q2=0 cвmв(t−tв)+cлmл(0−tл)+λmл+cвmл(t−0)=0 |
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 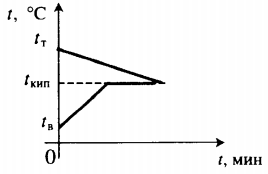
Уравнение теплового баланса: Q1+Q2=0 cтmт(100−tт)+cвmв(100−tв)+rmп=0 |
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 оС. | 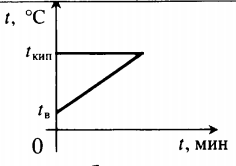
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmв(100−tв)=0 |
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 оС. | 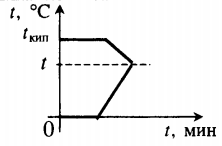
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmп(t−tкип)+λmл+cвmл(t−tпл)=0 |
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 оС, долили 3 л кипятка. Какая температура воды установилась?
2 л = 2 кг
3 л = 3 кг
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
cm1(t−t0)=−cm2(t−tкип)
Или:
m1(t−t0)=−m2(t−tкип)
m1t+m2t=m1t0+m2tкип
(m1+m2)t=m1t0+m2tкип
t=m1t0+m2tкипm1+m2
t=2·25+3·1002+3=3505=70 (°C)
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
| При неупругом ударе о стенку пуля нагрелась |
mv22=cmΔt |
| Тело падает с некоторой высоты и в момент падения нагревается |
mgh=cmΔt |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
0,5(mv202−mv22)=cmΔt |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
mv22=cmΔt+λm |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
0,6mgh=cmΔt+rm |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
qmтоп=mрgh |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
0,25qmтопmсv22 |
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0,52mv22=cmΔt
Δt=0,52v22c=0,52·10022·130=20 (К)
Примеры КПД
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. |
Qполезн=cmΔT Иногда: Qполезн=cmΔT+rm Wзатр=Pt (произведение мощности на время) |
η=cmΔTPt100% |
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. |
Qполезн=cmΔT Qзатр=qmтоп |
η=cmΔTqmтоп100% |
| Двигатель автомобиля, самолета. |
Aполезн=Nt=Nsv Qзатр=qmтоп |
η=cmΔTvqmтоп100 |
| Ружье с пороховым зарядом, пушка |
Eполезн=mv22 Qзатр=qmпор |
η=mv22qmпор100 |
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q1t1=Q2t2
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q1t1=Q2t2
Количество теплоты, сообщенное воде при нагревании:
Q1=сm(t2−t1)
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
Q1=rm
Отсюда:
сm(t2−t1)t1=rmt2
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
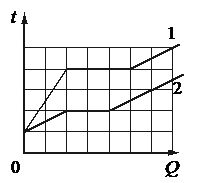
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера.
Ответ:
а) Температура плавления первого тела в 1,5 раза больше, чем второго.
б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии
в 3 раза больше, чем первого.
г) Оба тела имеют одинаковую удельную теплоту плавления.
д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вд
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать уравнение теплового баланса.
3.Выполнить решение в общем виде.
4.Определить и вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура льда: t1 = 0 oC.
• Конечная температура воды: t2 = 20 oC.
• Количество теплоты, переданное льду изначально: Q = 50 кДж.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.1k