Как найти массу, зная скорость
Умение определять массу движущегося тела может пригодиться не только на школьных уроках физики, но и в обычной жизни. Предположим, требуется поднять экскаватором автомобиль, масса которого неизвестна, при этом известна скорость, с которой машина будет поднята.

Инструкция
Воспользуйтесь формулой F=ma, где F – сила (измеряется в ньютонах), m – масса автомобиля, a – ускорение. Чтобы найти массу, примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Получится: m=F/a.
Теперь замените ускорение известной величиной – скоростью (V). Воспользуйтесь формулой a=V/t, где t – время, за которое поднимется машина. Если время дано в секундах, а скорость в метрах в минуту, то уравняйте величины. Переведите либо время в минуты, либо скорость в метры с секунду.
В исходную формулу m=F/a подставьте полученное значение ускорения. Получится: m=F/V/t. Воспользуйтесь правилом деления на дробь: «При делении на обычную дробь ее знаменатель уходит наверх, а числитель – вниз». Отсюда: m=Ft/V.
Теперь, чтобы найти массу, подставьте в формулу m=Ft/V известные значения. Например: F=50 Н (ньютонов), t=10 с (секунд), V=1 м/c (метров в секунду). Получится: m=50 Н х 10 с / 1 м/с, m=500 килограммов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Определите массу автомобиля, движущегося при торможении с ускорением 2
м
/
с
2
, если сила трения равна 6 кН.
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Второй закон Ньютона. Номер №1495
Решение
Получай решения и ответы с помощью нашего бота
Дано:
a = 2
м
/
с
2
;
F = 6 кН.
Найти:
m − ?
СИ:
F = 6 000 Н.
Решение:
По второму закону Ньютона:
a
=
F
m
;
m
=
F
a
;
m
=
6000
2
=
3000
кг.
Ответ: 3000 кг.
Масса представляет собой количество материи, которое содержится в каком-либо теле. В свою очередь материя – это нечто, что можно физически потрогать и ощутить. Как правило, массу связывают с размерами объекта, однако это не всегда верно. Например, земной шар мог бы быть большего размера, но иметь меньшую массу. В статье рассмотрен вопрос о том, как найти массу через объем и плотность.
Понятие массы и ее появление в физике
Перед тем как рассмотреть вопрос о том, как найти массу через объем и плотность, следует понять, откуда взялась масса в физике, и что она определяет. Сам термин “масса” происходит от латинского слова massa – глыба, вещество, тело, которое, в свою очередь, берет свое начало от греческого слова μᾶζα, буквально означающего “тесто”.
Масса – физическое понятие, которое указывает на количество содержащейся в теле материи. В Международной системе единиц измерения ее измеряют в килограммах. Появление в физике этого понятия связано с двумя важными законами:
- Закон всемирного тяготения.
- Второй закон Ньютона.
В соответствии с концепцией всемирного тяготения два тела притягиваются друг к другу с силой, которая пропорциональна произведению двух постоянных величин. Эти постоянные величины получили название гравитационных масс этих тел. То есть гравитационная масса тела – это свойство самой материи, благодаря которому все тела притягиваются друг к другу.
Что касается второго закона Ньютона, то следует вспомнить, что любое ускорение, вызванное действием некоторой внешней силы на данное тело, пропорционально некоторой константе, которая называется инертной массой. В этом законе инертная масса определяет меру “сложности” изменения скорости движения данного тела.
Понятие объема тела
Объем является физическим свойством материи, которое определяет занимаемое ею пространство. В Международной системе единиц он измеряется в метрах кубических, но также часто используют другие единицы измерения: кубические сантиметры и литры.
В зависимости от состояния вещества применяют различные методы измерения объема:
- Для жидких тел используют специальные градуированные прозрачные емкости (цилиндры, пробирки, пипетки и другие).
- Для твердых тел, которые сохраняют свою форму, объем измеряется исходя из их линейных размеров с применением соответствующей математической формулы. Например, параллелепипеда объем равен произведению его длины, ширины и высоты.
- Газообразные тела не сохраняют свой объем, в отличие от жидкостей и твердых тел, поэтому он для газов всегда равен объему сосуда, в котором находится газ.
Плотность вещества
Наконец, отвечая на вопрос о том, как найти массу через объем и плотность, следует разобраться с последней характеристикой – плотностью тел. Плотность является неотъемлемой физической характеристикой материи, которая связывает массу и объем, то есть она определяет, какое количество массы вещества содержится в единице объема. В Международной системе единиц она выражается в виде килограммов на метр кубический, но часто используется и в граммах на сантиметр кубический.
Любое вещество обладает конкретным значением плотности, например, в одном литре воды содержится один килограмм массы, то есть ее плотность равна 1 кг/л или 1000 кг/м3.
Понятие плотности играет важную роль в природе. Так, вопрос плавучести тел в воде является исключительно вопросом сравнения плотности тела и воды. Тела, имеющие большую плотность, чем вода, тонут в ней, например, яйцо или камень.
Как найти массу в физике через объем и плотность?
Перейдем теперь непосредственно к решению поставленной задачи. Допустим необходимо измерить массу имеющегося алмаза. Сначала нужно измерить его объем, допустим, он равен 5000 см3. Разбираясь в том, как найти массу через объем, следует также определить плотность вещества. В данном случае можно обратиться к табличным данным и посмотреть, какая плотность характерна для алмаза. В таблице находим, что она равна 3,52 г/см3.
После того как все необходимые величины определены, следует использовать известную формулу, как найти массу через объем и плотность: m = V*ρ, где V – объем тела, ρ – плотность. Подставляя полученные значения для алмаза, получаем: m = 5000 (см3)*3,52 (г/см3) = 17600.0 г = 17,6 кг. Следует обратить внимание, что при умножении объема на плотность единицы измерения объема (см3 в примере) сокращаются и остаются только единицы измерения массы.
Содержание:
- Определение и формула массы тела
- Инертная масса
- Гравитационная масса
- Формула расчета массы через плотность тела
- Масса в специальной теории относительности
- Примеры решения задач
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (mi):
$$m=sum_{i=1}^{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$bar{F}=m bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (Ft) избранного тела:
$$m=frac{F_{t}}{g}(3)$$
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
$$m=int_{V} rho d V(4)$$
где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:
$m = rho V (5)$
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Примеры решения задач
Пример
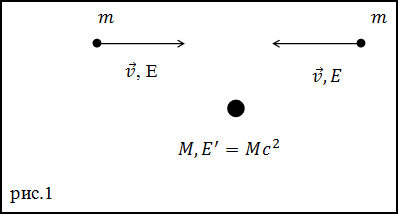
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
$$E^{prime}=M c^{2}(1.1)$$
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Как найти массу, зная скорость
Умение определять массу движущегося тела может пригодиться не только на школьных уроках физики, но и в обычной жизни. Предположим, требуется поднять экскаватором автомобиль, масса которого неизвестна, при этом известна скорость, с которой машина будет поднята.
Воспользуйтесь формулой F=ma, где F – сила (измеряется в ньютонах), m – масса автомобиля, a – ускорение. Чтобы найти массу, примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Получится: m=F/a.
Теперь замените ускорение известной величиной – скоростью (V). Воспользуйтесь формулой a=V/t, где t – время, за которое поднимется машина. Если время дано в секундах, а скорость в метрах в минуту, то уравняйте величины. Переведите либо время в минуты, либо скорость в метры с секунду.
В исходную формулу m=F/a подставьте полученное значение ускорения. Получится: m=F/V/t. Воспользуйтесь правилом деления на дробь: «При делении на обычную дробь ее знаменатель уходит наверх, а числитель – вниз». Отсюда: m=Ft/V.
Теперь, чтобы найти массу, подставьте в формулу m=Ft/V известные значения. Например: F=50 Н (ньютонов), t=10 с (секунд), V=1 м/c (метров в секунду). Получится: m=50 Н х 10 с / 1 м/с, m=500 килограммов.