|
Кусочек титана без полостей объёмом V=4 см³ опустили в воду. Плотность титана ρт=4,5 г/см³, плотность воды ρв=1,0 г/см³, плотность льда ρл=0,9 г/см³. Ускорение свободного падения g=10 м/с². 1) Определите массу металла. Ответ выразите в граммах, округлите до целых. 2) Определите силу тяжести, действовавшую на металл до погружения. Ответ выразите в ньютонах, округлите до сотых. 3) Определите выталкивающую силу, действующую на металл после полного погружения. Ответ выразите в ньютонах, округлите до сотых. 4) Как меняется при помещении в воду действующая на металл сила Архимеда?
5) Какая минимальная масса льда должна намёрзнуть на металл, чтобы такое тело плавало? Ответ выразите в г, округлите до целых. 1) Массу металла найти просто, он равна произведению объёма кусочка на плотность металла. Воспользуемся формулой: m=V*ρт m=4*4,5=18 г 2) Силу тяжести, которая действует на металл до погружения, найдём по формуле: Fтяж=mg Так как ответ нужно дать в Ньютонах, а 1 Н – это 1 кг*м/с², то массу нужно выразить в килограммах. m=18 г=0,018 кг Fтяж=0,018*10=0,18 Н 3) По закону Архимеда на тело, погружённое в жидкость, действует выталкивающая сила, которая равна весу объёма жидкости, который вытесняет тело. Это можно выразить формулой: FАрх=ρв·g·Vт FАрх=1000 кг/м³*10 м/с²*0,000004 м³=0,04 Н. 4) Сила Архимеда при погружении металла в воду увеличивается. 5) Металл с намёрзшим будет льдом плавать, полностью погрузившись в воду. Получим формулу: ρв·g·(Vл+Vт)=ρл·g·Vл+ρт·g·Vт Отсюда: ρв·Vл+ρв·Vт=ρл·Vл+ρт·Vт Подставим данные: 1*Vл+1*4=0,9*Vл+4,5*4 0,1Vл=14 Vл=140 см³ Знаете ответ? |
Смотрите также: ВПР физика 8 класс Задание 11 № 811 – какой ответ? ВПР по физике 8 класс 2020, задания, ответы, демоверсии, где найти? ВПР физика 8 класс. Как решить задачу про стрелочный амперметр? ВПР физика 8 класс. Как решить задачу про самодельный фонарик Жени? Физика 8 класс, Доклад на тему: “Круговорот воды в природе”, как написать? Физика 8 класс, Доклад на тему: “Лунное затмение”, как написать? Физика 8 класс, Доклад на тему: “Солнечное затмение”, как написать? ВПР Физика 8 класс, задание 2 № 26 – какой ответ? ВПР Физика 8 класс, задание если замёрзли руки, ответ – где найти? ВПР физика 8 класс. Как решить задачу про сопротивление клеточной мембраны? |
- вычислить массу чистой H2SO4:
Определить число молей H2SO4:
Составить уравнение данной реакции:
Исходя из равенства отношений количеств H2SO4 и BaSO4 к своим коэффициентам и преобразовав пропорцию, определить кол-во осаждённого BaSO4 в молях:
Вычислить массу осадка:
m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г
масса выпавшего осадка BaSO4 равна 69,9 г
Источник
Эквивалент. Закон зквивалентов. Определение эквивалентной массы вещества
Определение объема водорода
Задача № 11.
Некоторое количество металла, эквивалентная масса которого равна 27,9 г/моль, вытесняет из кислоты 700 мл водорода, измеренного при нормальных условиях. Определить массу металла.
Решение:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Та как водород находится в газообразном состоянии, то, соответственно, его количество измеряется в объёмных единицах (мл, л, м 3 ). Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 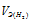
Тогда можно записать:
Ответ: 1,74г.
Определение эквивалентной массы вещества
Задача № 12.
1,60г кальция и 2,61г цинка вытесняют из кислоты одинаковые количества водорода. Вычислить эквивалентную массу цинка, зная, что эквивалентная масса кальция равна 20,0 г/моль.
Решение:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Ответ: 32,6г/моль.
Определение отношения масс реагирующих веществ
Задача № 13.
Серная и ортофосфорная кислоты имеют одинаковую молекулярную массу. Каково отношение масс этих кислот, пошедших на нейтрализацию одного и того же количества щелочи, если образовались соответственно сульфат и дигидроортофосфат?
Решение:
Формула сульфата имеет вид MeSO4, а дигидроортофосфата – MeH2PO4. Таким образом, на образование сульфата затрачивается две эквивалентные массы щёлочи, а на образование дигидроортофосфата – одна эквивалентная масса щёлочи. Так как H2SO4 с двумя эквивалентными массами щёлочи, то её эквивалентная масса в реакции нейтрализации равна М/2 г/моль, а фосфорная кислота реагирует с одной эквивалентной массой щёлочи, то её эквивалентная масса равна М/1г/моль. Отсюда, отношение мас этих кислот, с учётом, что их молекулярные массы равны будет иметь вид:
Это можно подтвердить уравнениями реакций нейтрализации этих кислот с гидроксидом натрия:
Задача № 14.
Медь образует два оксида. На определенное количество меди при образовании первого оксида пошло вдвое больше кислорода, чем при образовании второго. Каково отношение валентности меди в первом оксиде к ее валентности во втором?
Решение:
Согласно закону эквивалентов 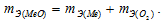
Таким образом, валентность меди в первом оксиде равна II, а во втором – I.
Ответ: 2 : 1.
Определение значения эквивалентной массы вещества
Задача № 15
При взаимодействии ортофосфорной кислоты со щелочью образовалась соль Na2HPO4. Найти для этого случая значение эквивалентной массы ортофосфорной кислоты.
Решение:
Уравнение реакции имеет вид:
Эквивалент (эквивалентная масса) кислоты равна мольной массе (М) делённой на число атомов водорода, замещённых в данной реакции на металл (на число вступающих в реакцию атомов водорода). Так как при взаимодействии ортофосфорной кислоты со щёлочью образовалась соль Na2HPO4, т.е. на натрий заместилось два атома водорода в кислоте H3PO4. Следовательно, эквивалентная масса ортофосфорной кислоты в реакции со щёлочью при образовании гидрофосфата натрия равна М/2 = М(H3PO4)/2 = 98/ 2 = 49г/моль.
Ответ: 49г/моль.
Задача № 16
На нейтрализацию 2,45г кислоты идет 2,00г гидроксида натрия. Определить эквивалентную массу кислоты.
Решение:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Эквивалентная масса гидроксида натрия равна М(NaOH)0/1 = 40г/моль.
Ответ: 49г/моль.
Задача № 17
При взаимодействии 5,95г некоторого вещества с 2,75г хлороводорода получилось 4,40г соли. Вычислить эквивалентные массы вещества и образовавшейся соли.
Решение:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Эквивалентная масса хлороводорода равна М(HCl) = 36,5/1 = 36,5г/моль.
Ответ: а) 58,4г/моль; б) 78,97 г/моль.
Определение эквивалентного объема водорода
Задача № 18.
0,376г алюминия при взаимодействии с кислотой вытеснили 0,468л водорода, измеренного при нормальных условиях. Определить эквивалентный объем водорода, зная, что эквивалентная масса алюминия равна 8,99 г/моль.
Решение:
Если одно из веществ находится в газообразном состоянии, то, соответственно, его количество измеряется в объёмных единицах (мл, л, м 3 ). Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Ответ: 11,2л/моль.
Источник
Расчеты концентрации
растворенных веществ
в растворах
Решение задач на разбавление растворов особой сложности не представляет, однако требует внимательности и некоторого напряжения. Тем не менее можно упростить решение этих задач, используя закон разбавления, которым пользуются в аналитической химии при титровании растворов.
Во всех задачниках по химии показаны решения задач, представленных как образец решения, и во всех решениях используется закон разбавления, принцип которого состоит в том, что количество растворенного вещества 
Рассмотрим проблему решения задач на разбавление, исходя из следующих соображений.
• Количество растворенного вещества 

где c – молярная концентрация растворенного вещества в моль/л, V – объем раствора в л.
• Масса растворенного вещества m(р.в.):
m(р. в.) = m(р-ра)•
где m(р-ра) – масса раствора в г, 
Обозначим в исходном (или неразбавленном) растворе величины c, V, m(р-ра), 
m1(р-ра), 

Составим уравнения разбавления растворов. Левые части уравнений отведем для исходных (неразбавленных) растворов, а правые части – для разбавленных растворов.
Неизменность количества растворенного вещества при разбавлении будет иметь вид:
Сохранение массы m(р. в.):
Количество растворенного вещества 

где M(р. в.) – молярная масса растворенного вещества в г/моль.
Уравнения разбавления (1) и (2) связаны между собой следующим образом:
с1•V1 = m2(р-ра)•
m1(р-ра)•
Если в задаче известен объем растворенного газа V(газа), то его количество вещества 

Уравнения разбавления примут соответственно вид:
V(газа)/22,4 = m2(р-ра)•
Если в задаче известны масса вещества или количество вещества, взятого для приготовления раствора, то в левой части уравнения разбавления ставится m(р. в.) или 
Если по условию задачи требуется объединить растворы разной концентрации одного и того же вещества, то в левой части уравнения массы растворенных веществ суммируются.
Довольно часто в задачах используется плотность раствора 
Приведем примеры решения «образцовых» задач.

Дано:
Найти:
Решение
Ответ. V1 = 50 мл.



Дано:

m2(р-ра) = 500 г, 
Найти:
Решение
m1(р-ра)•

Найдем массу добавляемой воды:
m(H2O) = 500 – 100 = 400 г.

(
Дано:


с2 = 0,35 моль/л,
V2 = 0,04 л,
М(H2SO4) = 98 г/моль.
Найти:
Решение
m1(р-ра)•
V1•

Подставляем значения известных величин:
Отсюда V1 = 0,01405 л, или 14,05 мл.
Ответ. V1 = 14,05 мл.


(или 10%)?
Дано:
V(р-ра) = 1 л,


М(HCl) = 36,5 г/моль.
Найти:
Решение
V(HCl)/22,4 = m(р-ра)•
V(HCl)/22,4 = V(р-ра)•

Отсюда V(HCl) = 64,44 л.
Найдем массу добавляемой воды:
m(H2O) = V(р-ра)•
m(H2O) = 1•1050 – 64,44/22,4•36,5 = 945 г.
Ответ. 64,44 л HCl и 945 г воды.

Дано:


М(NaOH) = 40 г/моль.
Найти:
Решение
m(р-ра)• 
m(р-ра)• 

Разделим обе части уравнения на m(р-ра) и подставим численные значения величин.
Отсюда c = 6,1 моль/л.
Ответ. c = 6,1 моль/л.

Дано:
m(Na2SO4) = 42,6 г,
m(H2O) = 300 г,

M(Na2SO4) = 142 г/моль.
Найти:
Решение
Подставляя численные значения, получим:
42,6 = с•(42,6 + 300)/1120•142.
Отсюда с = 0,98 моль/л.
Ответ. с = 0,98 моль/л.

Дано:



m3(р-ра) = 300 г.
Найти:
Решение
m1(р-ра)•


Поскольку m1(р-ра) + m2(р-ра) = 300 г, то получаем систему из двух уравнений с двумя неизвестными. Решая совместно два уравнения, находим:

Дано:
m1(NaF) = 4,1 г,
m2(NaF) = 4,5 г,
m2(р-ра) = 500 г,

(1 – 
Найти:
Решение
m2(р-ра)•(1 – 

Отсюда m1(р-ра) = 104,1/104,5•500 = 498,09 г,
m(NaF) = 500 – 498,09 = 1,91 г.
Ответ. m(NaF) = 1,91 г.
ЛИТЕРАТУРА
1. Хомченко Г.П., Хомченко И.Г. Задачи по химии для поступающих в вузы. М.: Новая волна, 2002.
2. Фельдман Ф.Г., Рудзитис Г.Е. Химия-9. М.: Просвещение, 1990, с. 166.
Источник
Adblock
detector
Содержание
- Весы под водой
- Читайте также
- РАБОТА С ТЯЖЕЛОЙ ВОДОЙ
- 61 Звук под водой
- 70 Шутка со стаканом и водой
- Глава вторая На воде и под водой
- Человек под водой
- 2. Читатель узнает, что и пенсы могут служить науке. Что скрывалось за «грязью» в сосуде. Две тысячи метров под водой. Последствие одной аварии. Привидение, которое не возвращается.
- надо узнать вес металлического бака, размеры: 1, 6 м х 1,5 м х 2м при толщине стенки 3 мм?
- Сила Архимеда
- Архимедова сила: что это такое и как действует
- «Эврика!» Открытие закона Архимеда
- Формула силы Архимеда
- Как действует сила Архимеда
- Сила Архимеда в жидкости: почему корабли не тонут
- Сила Архимеда в газах: почему летают дирижабли
- Когда сила Архимеда не работает
- Интересное по рубрике
- Найдите необходимую статью по тегам
- Подпишитесь на нашу рассылку
- Мы в инстаграм
- Рекомендуем прочитать
- Реальный опыт семейного обучения
Весы под водой
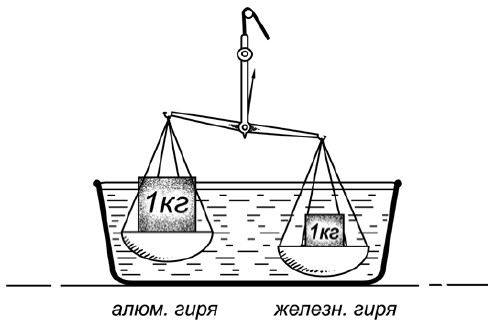
Килограммовую гирю можно изготовить и из железа, и из алюминия. Но так как алюминий примерно втрое легче железа, то при одинаковом весе гиря алюминиевая будет по объему втрое больше железной. Поставим на одну чашку весов железный килограмм, на другую – алюминиевый; весы, конечно, будут в равновесии. Теперь вообразите, что наши весы с гирями очутились под водою. Сохранится ли равновесие? Если нет, то которая чашка перетянет?
Чтобы ответить на этот вопрос, нужно вспомнить, что каждая вещь теряет в жидкости столько веса, сколько весит вытесняемая вещью жидкость.
В нашем случае чашки весов сами по себе теряют под водою одинаковый вес (они одной величины). Но гири теряют в весе не одинаково: крупная алюминиевая вытесняет больше воды, нежели мелкая железная; поэтому алюминиевая теряет в весе больше железной; останется же веса в алюминиевой гире меньше, чем в железной.
Рис. 40. Задача о весах под водою (ответ)
Значит, под водой весы никак не сохранят равновесия: чашка с железной гирей перетянет.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
РАБОТА С ТЯЖЕЛОЙ ВОДОЙ
РАБОТА С ТЯЖЕЛОЙ ВОДОЙ 8.55. В предыдущих главах уже упоминалось о преимуществах тяжелой воды в качестве замедлителя. Тяжелая вода лучше, чем графит, замедляет нейтроны и меньше, чем графит, их поглощает. Поэтому возможно построить аггрегат цепной реакции с тяжелой водой и
61 Звук под водой
61 Звук под водой Скорость распространения звука в воздухе мы уже знаем – примерно триста тридцать метров в секунду. А вот интересно, в воде звук распространяется быстрее или медленнее?Помните, я рассказывал про прохождение звука через стену? Так вот, чем более плотным
70 Шутка со стаканом и водой
70 Шутка со стаканом и водой Для опыта нам потребуются: обычный стакан с водой, квадратный кусок плотной бумаги. Это старинный опыт, не я его придумал, но, когда я спрашивал про него знакомых детей и их родителей, оказывается, его мало кто знает. Поэтому я решил тоже
Глава вторая На воде и под водой
Глава вторая На воде и под водой Почему киты живут в море? Задолго до того, как появился человеческий род, жили на суше животные таких больших размеров, каких нынешние сухопутные животные не достигают. Особенно крупны били ящеры, один из них – диплодок – имел 22 м в длину,
Человек под водой
Человек под водой Хотя в воде и растворен воздух, но организм наш так устроен, что дышать этим воздухом, как дышат рыбы, мы не можем. Чтобы оставаться под водою, человек должен либо иметь с собою запас воздуха, либо же быть в сообщении с воздухом, который имеется над водою.
2. Читатель узнает, что и пенсы могут служить науке. Что скрывалось за «грязью» в сосуде. Две тысячи метров под водой. Последствие одной аварии. Привидение, которое не возвращается.
2. Читатель узнает, что и пенсы могут служить науке. Что скрывалось за «грязью» в сосуде. Две тысячи метров под водой. Последствие одной аварии. Привидение, которое не возвращается. Одним из первых вступил на долгий и тернистый путь, ведущий к абсолютному нулю температуры,
Источник
Сколько весит металлический бак, если имеет размеры: 1, 6 м х 1,5 м х 2м при толщине стенки 3 мм? На
огороде стоит дырявый поливочный бак. Вот с мужем решаем: то ли его
сдать на металл и на вырученные деньги купить пластмассовый, который
очень быстро спионерят, то подремонтировать. Если короче, то мои
расчеты мужу не нравятся, говорит, что мало ))) насчитала. А я ж все по
правилам математики. Но, думаю, может, и правда, могзи уже не варят.
Помогите) ) )
зависит от плотности металла
Сколько весит бак металл диаметр 2 м, высота 1,5 м, S — 4 мм ?
выс ширина глубина, я пологаю написана, ну газелька маленькая может увезти в кузове, как ты короче примерно весишь
килограмм около 150. При такой толщине металла возможно сваркой залатать.
400 кг, денег хватит только лишь на добротную крышку от равноразмерного пластикого бака и на новый поливочный шланг.
Ответ: (160 + 160 + 150 + 150) х 200 х 0,3 см х 9,8 г/см3 = 364 560г = = = 364 кг. А почём у Вас мет/лом?
Подсчитайте обьем металла и умножьте на 7,85т. м3 это обьемный вес металла Альберт не прав 9,8 это ускорение свободного падения
Источник
Сила Архимеда
Расчет силы Архимеда, действующей на погруженное в жидкость тело. Создан по запросу пользователя
Калькулятор написан по запросу пользователя, который звучал так: «расчет веса цилиндра в жидкости».
В данном случае понятно, что речь идет о законе Архимеда
«На тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (называемая силой Архимеда)»
Дальше текст капитана Очевидность.
Понятно, что на тело действует сила тяжести, равная или . Если тело погрузить в воду, то сила Архимеда начнет компенсировать силу тяжести. И как видно из формулы, все будет зависеть от плотности тела. Если плотность тела больше плотности жидкости — оно утонет, если меньше — будет выскакивать из воды, пока силы не уравновесятся (сила Архимеда будет уменьшаться за счет уменьшения объема тела погруженного в жидкость). Часть объема, оставшегося под водой, будет определяться соотношением плотностей — если плотность тела в два раза меньше плотности жидкости, погрузится только половина объема. Ну тут все тривиально.
Теперь с весом — вес будет уменьшаться на величину силы Архимеда. Уже есть, что посчитать. Мы можем не знать плотности тела, но зная его объем можно найти силу Архимеда, на которую и будет уменьшен вес. А поскольку под весом у нас обычно понимают массу, заодно расчитаем, какая масса воды была вытеснена, т.е. на сколько килограмм «уменьшилась» масса тела, погруженного в жидкость.
Источник
Архимедова сила: что это такое и как действует
Рассказываем, почему железные корабли не тонут, а воздушные шары летают, что такое «эврика» и при чём здесь Дональд Дак.
Гениальный учёный Архимед, живший в древнегреческих Сиракузах в III веке до нашей эры, прославился среди современников как создатель оборонительных машин, способных перевернуть боевой корабль. Другое его изобретение, «Архимедов винт», по сей день остаётся важнейшей деталью гигантских буровых установок и кухонных мясорубок. Мир обязан Архимеду революционными открытиями в области оптики, математики и механики.
Его личность окутана легендами, порой весьма забавными. С одной из них мы и начнём нашу статью.
«Эврика!» Открытие закона Архимеда
Однажды царь Сиракуз Гиерон II обратился к Архимеду с просьбой установить, действительно ли его корона выполнена из чистого золота, как утверждал ювелир. Правитель подозревал, что мастер прикарманил часть драгоценного металла и частично заменил его серебром.
В те времена не существовало способов определить химический состав металлического сплава. Задача поставила учёного в тупик. Размышляя над ней, он отправился в баню и лёг в ванну, до краёв наполненную водой. Когда часть воды вылилась наружу, на Архимеда снизошло озарение. Такое, что учёный голышом выскочил на улицу и закричал «Эврика!», что по-древнегречески означает «Нашёл!».
Он предположил, что вес вытесненной воды был равен весу его тела, и оказался прав. Явившись к царю, он попросил принести золотой слиток, равный по весу короне, и опустить оба предмета в наполненные до краёв резервуары с водой. Корона вытеснила больше воды, чем слиток. При одной и той же массе объём короны оказался больше, чем объём слитка, а значит, она обладала меньшей плотностью, чем золото. Выходит, царь правильно подозревал своего ювелира.
Так был открыт принцип, который теперь мы называем законом Архимеда:
На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела.
Эта выталкивающая сила и называется силой Архимеда.
Формула силы Архимеда
На любой объект, погружённый в воду, действует выталкивающая сила, равная весу вытесненной им жидкости. Таким образом, вес объекта, погружённого в воду, будет отличаться от его веса в воздухе в меньшую сторону. Разница будет равна весу вытесненной воды.
Чем больше плотность среды — тем меньше вес. Именно поэтому погрузившись в воду, мы можем легко поднять другого человека.
Выталкивающая сила зависит от трёх факторов:
- плотности жидкости или газа (p);
- ускорения свободного падения (g);
- объёма погружённой части тела (V).
Сопоставив эти данные, получаем формулу:
Как действует сила Архимеда
Поскольку сила Архимеда, действующая на тело, зависит от объёма его погружённой части и плотности среды, в которой оно находится, можно рассчитать, как поведёт себя то или иное тело в определённой жидкости или газе.
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа.
Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно.
Сила Архимеда в жидкости: почему корабли не тонут
Корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Но если корабль получит пробоину и пространство внутри заполнится водой, то общая плотность судна увеличится, и оно утонет.
В подводных лодках существуют специальные резервуары, заполняемые водой или сжатым воздухом в зависимости от того, нужно ли уйти на глубину или подняться ближе к поверхности. Тот же самый принцип используют рыбы, наполняя воздухом специальный орган — плавательный пузырь.
На тело, плотно прилегающее ко дну, выталкивающая сила не действует. Это учитывают при подъёме затонувших кораблей. Сначала судно слегка приподнимают, позволяя воде проникнуть под него. Тогда давление воды начинает действовать на корабль снизу.
Но чтобы поднять корабль на поверхность, необходимо уменьшить его плотность. Разумеется, воздух в получившем пробоину корпусе не удержится. Поэтому его заполняют каким-нибудь лёгким веществом, например, шариками пенополистирола.
Примечательно, что эта идея впервые пришла в голову не учёным, а авторам диснеевского комикса, в котором Дональд Дак таким образом поднимает со дна яхту Скруджа Макдака. Датский инженер Карл Кройер (Karl Krøyer), впервые применивший метод на практике, по собственному признанию вдохновлялся «Утиными историями».
Сила Архимеда в газах: почему летают дирижабли
В воздухе архимедова сила действует так же, как в жидкости. Но поскольку плотность воздуха обычно намного меньше, чем плотность окружённых им предметов, выталкивающая сила оказывается ничтожно мала.
Впрочем, есть исключения. Воздушный шарик, наполненный гелием, стремится вверх именно потому, что плотность гелия ниже, чем плотность воздуха. А если наполнить шар обычным воздухом — он упадёт на землю. Плотность воздуха в нём будет такая же, как у воздуха снаружи, но более высокая плотность резины обеспечит падение шарика.
Этот принцип используется в аэростатах — воздушные шары и дирижабли наполняют гелием или горячим воздухом (чем горячее воздух, тем ниже его плотность), чтобы подняться, и снижают концентрацию гелия (или температуру воздуха), чтобы спуститься. На них действует та же выталкивающая сила, что и на подводные лодки. Именно поэтому перемещения на аэростатах называют воздухоплаванием.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS72021 вы получите бесплатный доступ к курсу физики 7 класса, в котором изучается архимедова сила.
Когда сила Архимеда не работает
- Если тело плотно прилегает к поверхности. Если между телом и поверхностью нет жидкости или газа — нет и выталкивающей силы. Именно поэтому подводным лодкам нельзя ложиться на илистое дно — мощности их двигателей не хватит, чтобы преодолеть давление толщи воды сверху.
- В невесомости. Наличие веса у жидкости или газа — обязательное условие для возникновения архимедовой силы. В состоянии невесомости горячий воздух не поднимается, а холодный не опускается. Поэтому на МКС создают принудительную конвекцию воздуха с помощью вентиляторов.
- В растворах и смесях. Если в воду налить спирт, на него не будет действовать сила Архимеда, хотя плотность спирта меньше плотности воды. Поскольку связь между молекулами спирта слабее, чем связь молекул воды, он растворится в воде, и образуется новая жидкость — водный раствор спирта.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Интересное по рубрике
Найдите необходимую статью по тегам
Подпишитесь на нашу рассылку
Мы в инстаграм
Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Рекомендуем прочитать
Реальный опыт семейного обучения
Звонок по России бесплатный
Пишите нам письма
Посмотреть на карте
Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.
Источник
Определение металла в изделии (монете) с помощью закона Архимеда
по его плотности.
Как известно многим рынок заполонили подделки,изготавливаемые из дешёвого металла.
Я попробую вам объяснить как определить металл изделия почти со 100% точностью с помощью закона Архимеда по его плотности.
НАМ ПОНАДОБИТСЯ:
1.Весы (довольно точные,у моих весов погрешность +- 0.01 грамм ).
2.Ёмкость с водой (у меня пластиковый стакан ёмкостью 200 мл).
3.Нитки (обычные нитки для привязывания изделия-монеты).
4.Калькулятор.
5.Испытуемые изделия (украшения,кольца,цепочки,у меня монеты).
6.Перчатки (не обязательно).
Я для исследования взял четыре монеты:
1. Один рубль 1921.
2. Один рубль 1896.
3. Один рубль 1764.
4. Три рубля 2010.
Оригиналы этих монет должны быть выполнены из серебра
(чистое серебро 999 пробы имеет плотность 10.5 грамм на сантиметр кубический,по этому всегда учитывайте пробу металла!
Для более низкой пробы (750,875,900,925) показания будут ниже).
Порядок действий:
1.Берём изделие (монету) взвешиваем её на весах,записываем значение.
2.Берём ёмкость с водой ставим на весы и обнуляем значение
(у меня это кнопка “TARE”).
3.Теперь монету привязываем ниткой и опускаем в стакан с водой который стоит у нас на весах с обнулённым значением.
4.Когда монета полностью опустилась в воду в подвешенном состоянии,на весах изменится значение с 0.00 на какое-то число,
это число так же записываем.
5.Теперь делим первое полученное число (чистый вес монеты)
на второе число (после взвешивание монеты в подвешенном состоянии в воде) это и будет плотность металла.
Таблицу плотности металлов можно найти в любом учебнике химии 9-11 класса или в интернете,я приведу некоторые значения тут (Г/СМ3):
Золото 19.3
Платина 21.4
Палладий 12
Серебро 10.5
Медь 8.92
Железо 7.86
Никель 8.9
Алюминий 2.6
Свинец 11.34
Олово 7.31
Хром 7.1
Цинк 7.1
Латунь 8.5-8.7
Мельхиор 8.9
Данный способ хорош для определения драгоценных металлов:
золото,серебро,платина,палладий-это тяжёлые металлы с плотностью больше 10,остальные металлы,как правило,имеет плотность меньше 9.
На этом всё,если есть вопросы-отвечу в комментариях.
Кусочек титана без полостей объёмом V=4 см3 опустили в воду. Плотность титана ρт=4.5 г/см3, плотность воды ρв=1.0 г/см3, плотность льда ρл=0.9 г/см33. Ускорение свободного падения g=10 м/с2.
Определите массу металла. Ответ выразите в граммах, округлите до целых.
Определите силу тяжести, действовавшую на металл до погружения. Ответ выразите в ньютонах, округлите до сотых.
Определите выталкивающую силу, действующую на металл после полного погружения. Ответ выразите в ньютонах, округлите до сотых.
Как меняется при помещении в воду действующая на металл сила Архимеда?
Увеличивается
Не изменяется
Уменьшается
Какая минимальная масса льда должна намёрзнуть на металл, чтобы такое тело плавало? Ответ выразите в г, округлите до целых.
Arnfinn ответил на вопрос 27.04.2023
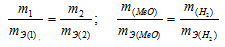
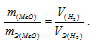
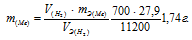
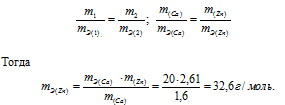
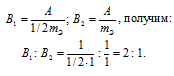
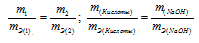
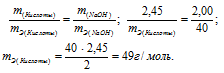
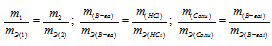
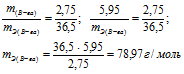
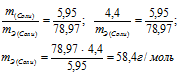
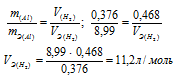









.png)













