Цель
– определение
массы нейтрального
0–мезона
по минимальному углу разлета
-квантов,
образующихся при его распаде.
ВВЕДЕНИЕ
Масса
частицы – фундаментальная характеристика,
определяющая как особенности ее
взаимодействия с другими микрообъектами,
так и (если частица нестабильна)
особенности ее распада. Большое значение
для теории элементарных частиц имеет
знание всего набора дискретных значений
масс частиц, встречающихся в природе.
Массу
частиц обычно определяют по их
кинематическим характеристикам: скорости
v,
импульсу Р,
кинетической T
или полной E
энергиям. Связь между этими величинами
и массой покоящейся частицы m
выражается хорошо известными из теории
относительности соотношениями:
, (18.1)
где
= v/c;
m,
Р,
T,
E
выражены в энергетических единицах.
Таким образом, чтобы определить массу
частицы, достаточно измерить любые две
ее кинематические характеристики.
Для
частиц, обладающих электрическим
зарядом, импульс Р
можно найти либо по измерениям радиуса
кривизны траектории частицы в магнитном
поле, либо по измерению среднего значения
квадрата угла многократного рассеяния
на ядрах. Кинетическую энергию частицы
T
с высокой точностью можно найти по
измерениям полного пробега в веществе,
скорость v
– либо по времени пролета частицей
определенного расстояния, либо по углу
испускания черенковского излучения,
либо измерением удельных ионизационных
потерь.
Массу
частиц с нулевым электрическим зарядом
можно определить с помощью кинематического
анализа реакций (как упругих, так и
неупругих), в которых эти частицы
принимают участие. При этом масса
ядра-мишени должна быть известна. Если
частица нестабильна, то ее масса может
быть измерена также с помощью
кинематического анализа продуктов ее
распада. Указанные методы обладают тем
достоинством, что они основаны на
применении точно выполняющихся законов
сохранения энергии, импульса. С их
помощью можно определить массы невидимых
на фотографиях частиц, если число
подлежащих вычислению величин (масса,
энергия, импульс частицы, углы, определяющие
направление движения) не превышает
четырех для всех частиц, участвующих в
реакции.
Для
измерения массы нейтрального -мезона
можно предложить несколько способов,
каждый из которых характеризуется
присущей только данному способу точностью
измерения. Простейшие из них основаны
на анализе кинематики распадов 0-мезонов.
Чтобы яснее представить себе их, укажем
основные свойства 0-мезона.
0-Мезон
– ядерно-активная частица, нейтральный
компонент изотопического триплета (+,
–,
0),
распадающийся за очень малые времена
( 10–16
с) по следующим каналам:
Большинство
экспериментальных методов измерения
массы 0-мезона
основаны на анализе кинематики основного
двухчастичного канала распада. При этом
кинематические характеристики -квантов,
а, следовательно, и методы определения
массы 0-мезона
зависят от того, будут ли образующиеся
в ядерных реакциях или распадах 0-мезоны
моноэнергетическими (т.е. с фиксированной
энергией) или нет.
Если
0-мезоны
– моноэнергетические, то энергетическое
распределение -квантов
имеет вид «столика» (рис. 18.1). У
экспериментальной кривой края
«столика» размываются из-за конечной
разрешающей способности конкретного
метода измерения. Ширина «размытия»
характеризует точность метода. Граничные
значения спектра -квантов
связаны с массой 0-мезона
и его импульсом соотношениями:
. (18.2)
Точность
определения массы 0-мезона
зависит от точности, с которой измерены
граничные значения энергии.
|
|
|
|
Рис. |
Рис. |
Для
моноэнергетических 0-мезонов
массу с высокой точностью можно получить
также из анализа распределения по углу
разлета -квантов.
Если полагать, что распад 0-мезона
в его системе покоя происходит изотропно,
то распределение -квантов
по углу их разлета
в лабораторной системе координат имеет
вид [9]:
, (18.3)
где
= P/E,
c = E/m.
Отсюда видно (рис. 18.2), что при фиксированной
энергии 0-мезона
угол разлета -квантов
не может принимать значения, меньше
некоторого минимального угла разлета .
Этот
угол можно найти из условия равенства
нулю подкоренного выражения (18.3):
или
.
Измеряя
угол мин,
можно определить значение массы
0-мезона.
Поскольку распределение dN/d
имеет резкий край, точность измерения
массы зависит лишь от точности, с которой
в эксперименте могут быть измерены углы
мин,
а также от степени моноэнергетичности
пучков.
В
случае, когда 0-мезоны
– немоноэнергетические, способ,
основанный на измерении минимального
угла разлета -квантов,
неприемлем, но тогда для определения
массы 0-мезона
по-прежнему можно воспользоваться
способом, основанным на измерении
граничных значений энергии -квантов.
При этом для определения массы 0-мезона
можно пользоваться соотношением (18.2).
В
данном случае граничные значения Eмин
и Eмакс
можно
определить экстраполяцией краев
экспериментального энергетического
спектра -квантов
к оси энергий (рис. 18.3).
|
|
Рис. |
Все
перечисленные выше кинематические
особенности распада 0-мезона
можно получить из рассмотрения импульсной
диаграммы распада [9].
ЭКСПЕРИМЕНТАЛЬНАЯ
УСТАНОВКА
Работа
проводится на снимках (стереофотографиях),
полученных с помощью 180-литровой
ксеноновой камеры ИТЭФ, размером
1034340
см3 (см.
работу 17). В работе используются снимки,
полученные при облучении камеры
K+-мезонами
с импульсом 850 МэВ/с. Моноэнергетические
0-мезоны,
необходимые для выполнения данной
работы, можно получить, отбирая такие
K+-мезоны,
которые останавливаются в камере и
затем распадаются по схеме
K+
+
+ 0.
При
этом можно считать, что K+-мезон
распадается в состоянии покоя, поскольку
время замедления K+-мезонов
(
10–13 с)
много меньше их среднего времени жизни
(K+ = 1,24 10–8
c).
Однако поскольку импульс первичных
K+-мезонов
высок, их пробег до остановки превышает
продольный размер камеры. Поэтому пучок
первичных K+-мезонов
нельзя использовать для решения
поставленной задачи. Это затруднение
можно обойти, если для получения
моноэнергетического пучка пионов
использовать вторичные K+-мезоны,
образовавшиеся в результате упругого
либо неупругого ядерного взаимодействия
первичного K+-мезона.
Общее количество таких случаев на пленке
длиной 400 кадров в данном эксперименте
равно 50.
Остановившиеся
K+-мезоны
дают характерную картину распада,
особенностью которой является наличие
следа от заряженного пиона в точке
распада и двух электрон-позитронных
пар (или комптоновских электронов),
образованных -квантами,
возникающими от распада нейтрального
пиона (эффективность регистрации
-квантов
в данной камере составляет 95 %). Типичный
случай отбираемого для измерения события
показан на рис. 18.4.
Характеристики
оптической системы 180-литровой камеры
следующие. Фотографирование следов
производится через смотровое стекло
из плексигласа размером 1005013
см3.
|
Рис. |
Рис. |
Стереофотоаппарат пузырьковой камеры
имеет три фотообъектива с фокусными
расстояниями 82 мм. Для данной работы
используются лишь две стереопроекции,
соответствующие крайним объективам.
Схема оптической системы камеры для
указанных объективов приведена на рис.
18.5.
Чтобы
определить угол разлета -квантов,
необходимо для каждого из отобранных
событий восстановить пространственную
картину. Эта задача обычно решается
либо с помощью специальных
просмотрово-измерительных устройств
стереокомпараторов, либо расчетным
путем (обычно с помощью ЭВМ) – определением
пространственных координат характерных
точек (точки распада K+-мезона,
точек конверсии -квантов)
по измеренным координатам этих точек
относительно положения оптических осей
на стереопроекциях. В данной лабораторной
работе для определения угла разлета
-квантов
используется следующая приближенная
формула:
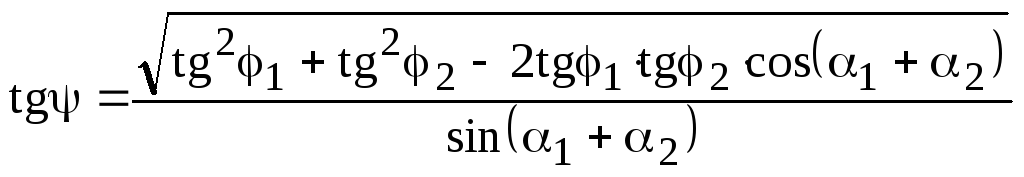
где
1
и 2
– проекции угла разлета
-квантов
на каждую плоскость проектирования, 1
и 2
– углы, под которыми видно исследуемое
событие каждым объективом (рис. 18.5).
Эта формула выведена в упрощающих
предположениях относительно проектирования,
осуществляемого при фотографировании,
а именно:
углы
проектирования 1
и 2
малы и полагаются равными для всех
рассматриваемых событий 1
2
6
27
(значения sin(1 +2)
для события, расположенного на оси
одного из объективов, и для события,
расположенного по середине между
объективами, различаются на 0,003);
искажения,
обусловленные преломлением оптических
сред малы. Таким образом, зная 1
и 2
и измеряя 1
и 2,
можно, рассчитав угол ,
построить распределение -квантов
по углу разлета.
ПОРЯДОК ВЫПОЛHЕHИЯ
РАБОТЫ
1. Отыскать
на стереоснимках события, соответствующие
случаям упругого либо неупругого
взаимодействия K+-мезонов
и последующего распада по схеме
K+
+ + 0
2.
2. Измерить
для каждого отобранного события значения
проекций углов разлета -квантов
– 1
и 2.
Результаты измерений свести в таблицу.
Общее количество измеренных распадов
должно быть 50.
ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕHИЙ
1. Рассчитать
значения углов
и построить график распределения
-квантов
по углу их разлета .
2.
Определить мин
и рассчитать массу 0-мезона,
предварительно вычислив импульс пиона,
образующегося при распаде остановившегося
K+-мезона.
3. По
экспериментальному распределению
оценить погрешность, с которой измеряется
угол мин,
и рассчитать погрешность, с которой
определена масса -мезона
в данной работе.
4. Сравнить
полученное значение массы 0-мезона
с табличными значениями. Дать качественную
характеристику использованного в данной
работе метода определения массы
0-мезона.
Соседние файлы в папке Chast_3
- #
- #
- #
- #
- #
- #
- #
§ 3.8 Состав и масса элементарных частиц
Последовательная теория элементарных частиц, которая предсказывала бы возможные значения масс элементарных частиц и другие их внутренние характеристики, ещё не создана.
Советский Энциклопедический Словарь
В настоящее время известно более сотни элементарных частиц [85, 86]. Это изобилие давно привело к мысли, что частицы отнюдь не элементарны, а состоят из ещё более простых элементов. Полагали, что этими элементами должны быть кварки, — гипотетические частицы с невероятными свойствами. Так, любой из кварков много тяжелей частицы, которую они образуют: часть больше целого! Поэтому многие считают, что гипотеза кварков и так называемая квантовая хромодинамика — это чисто формальный способ систематизации частиц. Ну, а такая фундаментальная характеристика частиц как масса, почему-то игнорируется учёными. А, ведь, именно массы позволили Д.И. Менделееву навести порядок в мире химических элементов, среди многих десятков которых царил некогда такой же хаос. На основе известных масс элементов не только была построена их система (таблица Менделеева), но и понято строение атома. Далее покажем, что и для понимания строения элементарных частиц их масса и закон её сохранения, вводимый БТР, может иметь ключевое значение.
Прежде всего, естественно допустить, что наиболее просты и элементарны частицы, обладающие наименьшей массой (так и среди атомов самый простой — водородный). К ним можно отнести электрон, массу М которого обычно берут за единицу измерения масс других частиц (М=1), и мельчайшие из мезонов [86]. А, именно, мюон (?-мезон) — заряженная частица, которая тяжелей электрона в 207 раз (M=207), нейтральный пион (?0-мезон, M=264) и заряженный пион (?+– или ?—-мезон с M=273). Думается, именно из этих частиц, как из деталек конструктора, и построены все прочие элементарные частицы, имеющие более высокие значения массы.
И, точно, беря эти три вида мезонов в разных сочетаниях, можно получить массу любой другой частицы. Например, два заряженных и два нейтральных пиона дают в сумме массу 1074,4. Это с точностью до 0,04 % совпадает с массой ?0-мезона (M=1074). Так что, эта частица состоит, вероятно, из четырёх пионов: ?+, ?—, ?0, ?0. Недаром, ?0-мезон распадается всегда именно на пионы. Другой пример: 8 заряженных пионов дают в сумме массу 273?8= 2184 — это масса ?0-гиперона, отличная от истинной всего на 0,03 %. Значит, лямбда-гиперон состоит из четырёх положительных и четырёх отрицательных пионов: ?0=4?+ + 4?—.
Судя по точности и частоте таких совпадений, они — не случайны и должны открыть тайну строения частиц. Для этого достаточно составить несложную компьютерную программу, по-разному комбинирующую массы трёх мезонов (M=207; 264; 273) и находящую совпадения их сумм с известными массами элементарных частиц. Результаты поиска программы сведены в систему (Таблица 2). В первой колонке стоит обозначение частицы, в следующих трёх — её состав (по числу мезонов), в пятой — расчётная масса, в шестой — измеренная, в седьмой — их разница в процентах, не превосходящая 0,2 %.
Из таблицы видно, что некоторые частицы (?0, ?*, ?*, ?—, ?—) можно представить несколькими комбинациями — разными наборами мезонов. Как легко заметить, причина этого в том, что сумма масс 4-х мюонов и ?0-мезона почти равна массе 4-х заряженных пионов (M=1092). Это означает, что и сами мезоны — это не элементарные, а составные частицы. Так, нейтральный пион должен, видимо, состоять из четырёх нейтральных частиц, имеющих массу 264/4=66 масс электрона. И каждая такая частица в сочетании с мюоном образует заряженный пион с массой M=207+66 =273 (Рис. 116).
Рис. 116. Состав и схемы распада пионов, следующие из соотношения их масс.
Эти частицы с М=66 пока никем не найдены, поэтому считают, что при распаде нейтрального пиона его масса просто исчезает, полностью переходя в гамма-излучение. Согласно БТР, это невозможно (§ 1.16), и, потому, при распаде пион должен делиться на те самые 4 частицы с М=66, которые лишь потому не открыты, что нейтральны и не оставляют следов в детекторах частиц, если только не считать их следами гамма-излучение. В дальнейшем будем для удобства называть эти частицы “гамма-мезонами” (или “гаммонами”), обозначая греческой ?, ввиду того, что эти продукты распада пионов долгое время принимали за гамма-кванты. В ядерной физике такое случалось и прежде: рождённые распадом нейтроны из-за их нейтральности и трудноуловимости тоже поначалу приняли за гамма-кванты. Наличие гаммона и мюона в составе заряженного пиона подтверждается тем, что последний при распаде образует мюон. Оставшаяся масса 273–207=66, как считают, переходит в энергию. Но, с позиций классической физики, в которой масса сохраняется, следует считать, что эту массу незаметно уносит гаммон.
В таком случае, разные варианты устройства одной и той же частицы окажутся эквивалентны. К примеру, уже рассмотренный ?0-гиперон состоит просто из 8-ми мюонов и 8-ми гаммонов, а лишние варианты отпадут. У иных же частиц, напротив, не нашлось даже одного точного способа представления комбинацией мезонов. Таковы нейтрон n, K-мезоны, ?0-гиперон и некоторые из частиц-резонансов. Есть, правда, сочетания мезонов, дающие массу почти как у этих частиц (с разницей примерно в 1 %). Однако, неидеальность таких совпадений говорит об их случайности, и программа отсеивает эти варианты, как маловероятные.
Но мы не учли другой возможности. Ведь в мире, помимо частиц, существуют античастицы, такие как позитрон, имеющие, возможно, отрицательную массу (§ 1.6). Раз масса — это количество материи, то у антиматерии масса — минусовая (§ 1.17). Этим же, с позиций классической физики и закона сохранения массы, можно объяснить бесследное исчезновение масс при аннигиляции частиц и античастиц, или, напротив, их рождение. Если в состав частицы, наряду с мезонами, иногда входят антимезоны, имеющие минусовую массу, то числу мезонов в частице можно придавать и отрицательные значения, что породит новые варианты. К примеру, 6 мюонов и один нейтральный антипион дают в сумме массу 206,7?6–264=976,1, что, с погрешностью в 0,2 %, совпадает с массой K0-мезона (M=974,1). А 6 мюонов в сумме с заряженным антипионом дают массу 206,7?6–273,1=967,1 одного заряженного K+-мезона (M=966,4), с погрешностью в 0,07 %. Поэтому, Таблица 2 дополнится новой (Таблица 3), где знаки минус соответствуют античастицам с антимассой.
Как видим, допустив существование отрицательной массы, можно и оставшиеся частицы представить в виде наборов из 3-х типов мезонов. Причём, античастиц в любом наборе — не больше двух. Если же все пионы разбить на гаммоны и мюоны (?0=4?; ?+=?+?) и представлять каждую частицу в виде набора из двух типов мезонов (? и ?), то во многих из таких комбинаций отрицательные массы исчезнут. Так, ?+=7?+5?; ?—=?+11?; ?0=17?+7?. А в оставшихся случаях от минусовых масс можно избавиться, допустив, что гаммоны есть и в составе мюонов, то есть мюоны — сами составные. Действительно, как увидим в дальнейшем, вполне можно обойтись без минусовых масс, которые до сих пор служили лишь удобным формальным приёмом, и в дальнейшем будут совершенно упразднены (§ 3.20). И позитрон, и другие античастицы имеют положительную инертную и гравитационную массу (§ 1.17). Поэтому, масса частицы всегда складывается из положительных масс образующих её частиц, в том числе электронов и позитронов.
Так или иначе, массу любой частицы всегда можно представить в виде M=66x+207y, где x — число ?-мезонов, а y — ?-мезонов. Придавая x и y различные целые значения, — составляя разные сочетания ?- и ?-мезонов, по-разному комбинируя их, — можно предсказать новые частицы, по крайней мере, узнать их массы. Впрочем, не всякая комбинация мезонов реализуется в природе, поскольку не все такие комбинации устойчивы. Точно так же, теоретически возможны ядра, состоящие из любого числа протонов и нейтронов. Однако, лишь редкие их сочетания оказываются стабильными, устойчивыми. Другие сочетания-изотопы, хоть и менее стабильны, но тоже живут некоторое время. А все прочие сочетания протонов и нейтронов крайне неустойчивы и распадаются почти мгновенно. То же и у сочетаний мезонов: одни из образованных ими элементарных частиц живут сравнительно долго, другие — малоустойчивы и сразу распадаются. Таковы, например, частицы-резонансы (?, ?, ?-частицы и все помеченные звёздочкой).
Может удивить, что в распадах, помимо мезонов, возникают и более крупные частицы. Но это — естественно, если фрагменты, на которые делится частица, состоят из нескольких мезонов. Ведь и тяжёлые атомные ядра при распаде делятся не на десятки отдельных протонов и нейтронов, а на образованные из них сравнительно крупные осколки (Рис. 114). Потому и продукты деления тяжёлых частиц — это, в основном, другие тяжёлые, составные частицы (Рис. 117). А возникающие в распадах пионы и мюоны — это лишь дополнительные мелкие осколки (вроде нейтронов, вылетающих при делении тяжёлых ядер). Образуются и совсем незаметные осколки деления (к примеру, гаммоны), чем вызвано кажущееся уменьшение массы в распадах.
Рис. 117. Распад ядра или элементарной частицы на осколки разной величины, идущий двояким путём.
Кроме соответствия массы, в комбинации надо обеспечить соответствие заряда. Поэтому, в комбинации мезонов, представляющей нейтральную частицу, должно быть поровну положительных и отрицательных зарядов. Например: ?0=2?0+?—+?+; ?0=4?++4?—. Если же число зарядов нечётное, то комбинацию можно сделать нейтральной, дополнив её одним электроном или позитроном. Зато, в составе заряженной частицы зарядов одного знака должно быть на один больше, чем другого. В этом случае, комбинации с чётным числом зарядов надо дополнить электроном или позитроном. Добавление этих частиц с M=±1 мало влияет на полную массу комбинации, поэтому, до сих пор мы их не привлекали: их назначение — обеспечить в первую очередь соответствие заряда, а не массы. Так, частицы-резонансы (?, ?*, ?*, ?*, ?*), имея строго заданную массу, могут обладать зарядом 0, ±1, ±2,— всё зависит от числа электронов и позитронов в комбинации. Тем, что помимо мезонов в каждую частицу могут дополнительно входить ещё несколько электронов или позитронов, можно объяснить и небольшие (порядка единицы) расхождения между расчётными и измеренными массами. Вообще же, массы некоторых частиц, особенно резонансов, известны с заметной погрешностью.
При делении частицы образующие её мезоны могут разбиться на разные сочетания. Такая частица распадается несколькими путями: в одних случаях давая одни продукты, в других — другие (Рис. 117). Физики считают это доказательством превращения частиц, — совсем как алхимики, видевшие в химических реакциях превращения веществ, хотя реально шла лишь перегруппировка атомов. Аналогично, “превращения” частиц вызваны перегруппировкой мезонов: мезонный состав частицы можно разбить на две-три группы разными способами, эти группы образуют разные частицы. В конце концов, ведь и тяжёлые ядра распадаются несколькими путями. Какие из частиц возникают в распаде чаще, зависит от устойчивости данных сочетаний мезонов, от энергии их связи в частице, а, значит, и от энергии распада.
Итак, выяснили, что почти все частицы построены из мезонов. Даже экспериментально мезоны были найдены, скажем, — в нейтронах, в форме окружающей их мезонной оболочки и отдельных точечных зарядов (партонов), на которых происходило рассеяние при зондировании [165]. Сами мезоны тоже не элементарны, и могут быть, в свою очередь, образованы электронами и позитронами (§ 3.9).
Теперь видно, насколько эффективны классические представления БТР — и в микромире. Именно они ведут к пониманию структуры элементарных частиц, чего не позволяла сделать квантовая механика. Ещё Дж. Фокс [2] указал на огромный потенциал теории Ритца в объяснении явлений микромира. По мнению Фокса, большой объём эмпирических данных: масс, времён жизни, структур элементарных частиц, — может найти истолкование именно в теории Ритца. Но из-за слепой веры учёных в теорию относительности, отказа от закона сохранения массы, открытого Ломоносовым (§ 3.13), современная наука не в силах объяснить точных соотношений между массами частиц и показать, почему масса данной частицы такая, а не иная. А для БТР это не проблема, так же, как и кинематика высоких скоростей, и дефект масс, и прочие законы микромира, возможные якобы лишь по СТО. И, хотя некоторые ядерные эксперименты приводят в качестве опровергающих БТР [153], они противоречат теории Ритца не больше, чем космические наблюдения (Часть 2). Дж. Фокс показал, что несоответствие чаще возникает не по вине БТР, а от неразвитости наших представлений о микромире и космосе. Привлекать явления для проверки теории Ритца можно, лишь пересмотрев их на её базе. А, если БТР раскроет строение частиц, к примеру, — нейтрона, то сразу откроются и новые источники энергии (§ 5.8).
Читайте также
5.2. Каталог элементарных действий
5.2. Каталог элементарных действий
Если вы разрабатываете интерфейс, то должны знать палитру всех его возможностей, аналогично тому, как художник имеет на своей палитре набор всех возможных красок. Спектр элементарных действий, которые пользователь может выполнить,
28. Средняя молярная масса смеси газов
28. Средняя молярная масса смеси газов
Уравнение для нахождения удельной газовой постоянной смеси:R = еgiRi= 8314,2(g1/ M1+ g2/ M2+… + gn/ Mn)Зная молярную массу смеси, можно найти газовую постоянную смеси:R = 8,314 / M.Зная объемный состав смеси, получим следующие формулы:gi= (R / Ri),еgi = Rе(ri / Ri) =
НЕПОКОРНЫЙ СОСТАВ
НЕПОКОРНЫЙ СОСТАВ
Получилось нечаянно взрывчатое вещество.В такую тесную смесь перемешалось горючее с кислородом, что сгорела она в один миг — какое там! — в одну тридцатитысячную мига. В тридцать тысяч раз быстрее, чем успеет мигнуть человек. В одну стотысячную секунды
8.2.3.1.8 Цвет, масса и качество бумаги
8.2.3.1.8 Цвет, масса и качество бумаги
Должны быть определены цвет, масса и качество (номер) бумаги, используемой для документации.Примечание — Если требуется конкретный номер бумаги, это должно быть
§ 3.9 Кристаллическое строение элементарных частиц и их распады
§ 3.9 Кристаллическое строение элементарных частиц и их распады
А если и в самом деле, протоны и нейтроны как кирпичики ядерных конструкций сложены из электронов и позитронов?… то могли же нуклоны возникнуть в виде кубических квазикристаллических образований,
§ 3.1 °Cистематизация и периодический закон элементарных частиц
§ 3.1 °Cистематизация и периодический закон элементарных частиц
Главный интерес химии — в изучении основных качеств элементов. А так как их природа нам ещё вовсе неизвестна и так как для них мы поныне твёрдо знаем только два измеряемые свойства: способность давать
§ 3.14 Гипотеза индуцированных распадов ядер и частиц
§ 3.14 Гипотеза индуцированных распадов ядер и частиц
Радиоактивный распад вызывается не разрушением ядра атома, а скорее является вторичным эффектом воздействия внешнего излучения, которые можно разделить на два типа: энергию сохранённую и энергию, поступающую
§ 4.11 Волновые свойства частиц
§ 4.11 Волновые свойства частиц
Его богатое воображение, его оптимистическая готовность овладеть проблемой, не затруднённые слишком критическим подходом, были бы здесь весьма уместны.
А. Зоммерфельд по поводу ранней кончины В. Ритца [50]
Вальтер Ритц, подобно Шерлоку
§ 5.9 Создание новых веществ, элементов, частиц
§ 5.9 Создание новых веществ, элементов, частиц
Хотя атомы остаются неизменными в химических процессах, когда-нибудь будет найден сильный и тонкий агент, позволяющий разбить атомы на ещё меньшие частицы и превратить одни атомы в другие.
Р. Бойль
Велика может быть роль
Состав оборудования
Состав оборудования
В составе систем дистанционного запуска (рис. 4.2) обязательно присутствуют силовые реле, коммутирующие токи силой в 30–40 А. Эти реле могут быть встроены в корпус центрального блока системы или быть внешними, скомпонованными в единую группу. С их
1.3. Состав документа
1.3. Состав документа
1.3.1. Документ (часть документа) включает:титульный лист;заглавный лист;содержание;основной текст;приложения;список литературы;лист регистрации изменений.1.3.2. Необходимость выполнения титульного листа зависит от уровня согласования (утверждения)
III. Масса, пространство и другие формальные категории Книга третья, рассказывающая о чувствах, пробуждаемых в нас зодчеством
III. Масса, пространство и другие формальные категории
Книга третья, рассказывающая о чувствах, пробуждаемых в нас зодчеством
В первой книге, да и отчасти во второй мы говорили преимущественно о языке архитектуры. Как будто само здание или его автор что-то хотят нам
4.12. ДИНАМИКА СВОБОДНЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ И ТЕЛ В ЭМП
4.12. ДИНАМИКА СВОБОДНЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ И ТЕЛ В ЭМП
Длительный период исследования взаимодействия заряженных частиц и ЭМП носили академический характер и представляли интерес только с точки зрения дополнительного развития теории ЭМП. Однако для ТЭ даже эти разработки
This article is about the subatomic particle. For the software, see Meson (software).

Mesons of spin 0 form a nonet |
|
| Composition | composite: quarks and antiquarks |
|---|---|
| Statistics | bosonic |
| Family | hadron |
| Interactions | strong, weak, electromagnetic and gravity |
| Theorized | Hideki Yukawa (1935) |
| Discovered | 1947 |
| Types | ~140 (List) |
| Mass | from 134.9 MeV/c2 ( π0 ) to 9.460 GeV/c2 ( ϒ ) |
| Electric charge | −1 e, 0 e, +1 e |
| Spin | 0, 1 |
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, they have a meaningful physical size, a diameter of roughly one femtometre (10−15 m),[1] which is about 0.6 times the size of a proton or neutron. All mesons are unstable, with the longest-lived lasting for only a few tenths of a nanosecond. Heavier mesons decay to lighter mesons and ultimately to stable electrons, neutrinos and photons.
Outside the nucleus, mesons appear in nature only as short-lived products of very high-energy collisions between particles made of quarks, such as cosmic rays (high-energy protons and neutrons) and baryonic matter. Mesons are routinely produced artificially in cyclotrons or other particle accelerators in the collisions of protons, antiprotons, or other particles.
Higher-energy (more massive) mesons were created momentarily in the Big Bang, but are not thought to play a role in nature today. However, such heavy mesons are regularly created in particle accelerator experiments that explore the nature of the heavier quarks that compose the heavier mesons.
Mesons are part of the hadron particle family, which are defined simply as particles composed of two or more quarks. The other members of the hadron family are the baryons: subatomic particles composed of odd numbers of valence quarks (at least 3), and some experiments show evidence of exotic mesons, which do not have the conventional valence quark content of two quarks (one quark and one antiquark), but 4 or more.
Because quarks have a spin 1/2, the difference in quark number between mesons and baryons results in conventional two-quark mesons being bosons, whereas baryons are fermions.
Each type of meson has a corresponding antiparticle (antimeson) in which quarks are replaced by their corresponding antiquarks and vice versa. For example, a positive pion (
π+
) is made of one up quark and one down antiquark; and its corresponding antiparticle, the negative pion (
π−
), is made of one up antiquark and one down quark.
Because mesons are composed of quarks, they participate in both the weak interaction and strong interaction. Mesons with net electric charge also participate in the electromagnetic interaction. Mesons are classified according to their quark content, total angular momentum, parity and various other properties, such as C-parity and G-parity. Although no meson is stable, those of lower mass are nonetheless more stable than the more massive, and hence are easier to observe and study in particle accelerators or in cosmic ray experiments. The lightest group of mesons is less massive than the lightest group of baryons, meaning that they are more easily produced in experiments, and thus exhibit certain higher-energy phenomena more readily than do baryons. But mesons can be quite massive: for example, the J/Psi meson (
J/ψ
) containing the charm quark, first seen 1974,[2][3] is about three times as massive as a proton, and the upsilon meson (
ϒ
) containing the bottom quark, first seen in 1977,[4] is about ten times as massive.
History[edit]
From theoretical considerations, in 1934 Hideki Yukawa[5][6] predicted the existence and the approximate mass of the “meson” as the carrier of the nuclear force that holds atomic nuclei together.[7] If there were no nuclear force, all nuclei with two or more protons would fly apart due to electromagnetic repulsion. Yukawa called his carrier particle the meson, from μέσος mesos, the Greek word for “intermediate”, because its predicted mass was between that of the electron and that of the proton, which has about 1,836 times the mass of the electron. Yukawa or Carl David Anderson, who discovered the muon, had originally named the particle the “mesotron”, but he was corrected by the physicist Werner Heisenberg (whose father was a professor of Greek at the University of Munich). Heisenberg pointed out that there is no “tr” in the Greek word “mesos”.[8]
The first candidate for Yukawa’s meson, in modern terminology known as the muon, was discovered in 1936 by Carl David Anderson and others in the decay products of cosmic ray interactions. The “mu meson” had about the right mass to be Yukawa’s carrier of the strong nuclear force, but over the course of the next decade, it became evident that it was not the right particle. It was eventually found that the “mu meson” did not participate in the strong nuclear interaction at all, but rather behaved like a heavy version of the electron, and was eventually classed as a lepton like the electron, rather than a meson. Physicists in making this choice decided that properties other than particle mass should control their classification.
There were years of delays in the subatomic particle research during World War II (1939–1945), with most physicists working in applied projects for wartime necessities. When the war ended in August 1945, many physicists gradually returned to peacetime research. The first true meson to be discovered was what would later be called the “pi meson” (or pion). During 1939–1942, Debendra Mohan Bose and Bibha Chowdhuri exposed Ilford half-tone photographic plates in the high altitude mountainous regions of Darjeeling, and observed long curved ionizing tracks that appeared to be different from the tracks of alpha particles or protons. In a series of articles published in Nature, they identified a cosmic particle having an average mass close to 200 times the mass of electron.[9] This discovery was made in 1947 with improved full-tone photographic emulsion plates, by Cecil Powell, Hugh Muirhead, César Lattes, and Giuseppe Occhialini, who were investigating cosmic ray products at the University of Bristol in England, based on photographic films placed in the Andes mountains.[10] Some of those mesons had about the same mass as the already-known mu “meson”, yet seemed to decay into it, leading physicist Robert Marshak to hypothesize in 1947 that it was actually a new and different meson. Over the next few years, more experiments showed that the pion was indeed involved in strong interactions. The pion (as a virtual particle) is also believed to be the primary force carrier for the nuclear force in atomic nuclei. Other mesons, such as the virtual rho mesons are involved in mediating this force as well, but to a lesser extent. Following the discovery of the pion, Yukawa was awarded the 1949 Nobel Prize in Physics for his predictions.
For a while in the past, the word meson was sometimes used to mean any force carrier, such as “the Z0 meson”, which is involved in mediating the weak interaction.[11] However, this use has fallen out of favor, and mesons are now defined as particles composed of pairs of quarks and antiquarks.
Overview[edit]
Spin, orbital angular momentum, and total angular momentum[edit]
Spin (quantum number S) is a vector quantity that represents the “intrinsic” angular momentum of a particle. It comes in increments of 1/2 ħ.[A]
Quarks are fermions—specifically in this case, particles having spin 1/2 ( S = 1/2 ). Because spin projections vary in increments of 1 (that is 1 ħ), a single quark has a spin vector of length 1/2, and has two spin projections, either ( Sz = +1/2 or Sz = −+1/2 ). Two quarks can have their spins aligned, in which case the two spin vectors add to make a vector of length S = 1 , with three possible spin projections ( Sz = +1, Sz = 0, and Sz = −1), and their combination is called a vector meson or spin-1 triplet. If two quarks have oppositely aligned spins, the spin vectors add up to make a vector of length S = 0, and only one spin projection ( Sz = 0 ), called a scalar meson or spin-0 singlet. Because mesons are made of one quark and one antiquark, they are found in triplet and singlet spin states. The latter are called scalar mesons or pseudoscalar mesons, depending on their parity (see below).
There is another quantity of quantized angular momentum, called the orbital angular momentum (quantum number L), that is the angular momentum due to quarks orbiting each other, and also comes in increments of 1 ħ. The total angular momentum (quantum number J) of a particle is the combination of the two intrinsic angular momentums (spin) and the orbital angular momentum. It can take any value from J = |L − S| up to J = |L + S| , in increments of 1.
| S | L | P | J | JP |
|---|---|---|---|---|
| 0 | 0 | − | 0 | 0− |
| 1 | + | 1 | 1+ | |
| 2 | − | 2 | 2− | |
| 3 | + | 3 | 3+ | |
| 1 | 0 | − | 1 | 1− |
| 1 | + | 2, 0 | 2+, 0+ | |
| 2 | − | 3, 1 | 3−, 1− | |
| 3 | + | 4, 2 | 4+, 2+ |
Particle physicists are most interested in mesons with no orbital angular momentum (L = 0), therefore the two groups of mesons most studied are the S = 1; L = 0 and S = 0; L = 0, which corresponds to J = 1 and J = 0, although they are not the only ones. It is also possible to obtain J = 1 particles from S = 0 and L = 1. How to distinguish between the S = 1, L = 0 and S = 0, L = 1 mesons is an active area of research in meson spectroscopy.[12]
P-parity[edit]
P-parity is left-right parity, or spatial parity, and was the first of several “parities” discovered, and so is often called just “parity”. If the universe were reflected in a mirror, most laws of physics would be identical—things would behave the same way regardless of what we call “left” and what we call “right”. This concept of mirror reflection is called parity (P). Gravity, the electromagnetic force, and the strong interaction all behave in the same way regardless of whether or not the universe is reflected in a mirror, and thus are said to conserve parity (P-symmetry). However, the weak interaction does distinguish “left” from “right”, a phenomenon called parity violation (P-violation).
Based on this, one might think that, if the wavefunction for each particle (more precisely, the quantum field for each particle type) were simultaneously mirror-reversed, then the new set of wavefunctions would perfectly satisfy the laws of physics (apart from the weak interaction). It turns out that this is not quite true: In order for the equations to be satisfied, the wavefunctions of certain types of particles have to be multiplied by −1, in addition to being mirror-reversed. Such particle types are said to have negative or odd parity (P = −1, or alternatively P = −), whereas the other particles are said to have positive or even parity (P = +1, or alternatively P = +).
For mesons, parity is related to the orbital angular momentum by the relation:[13][14]
where the L is a result of the parity of the corresponding spherical harmonic of the wavefunction. The “+1” comes from the fact that, according to the Dirac equation, a quark and an antiquark have opposite intrinsic parities. Therefore, the intrinsic parity of a meson is the product of the intrinsic parities of the quark (+1) and antiquark (−1). As these are different, their product is −1, and so it contributes the “+1” that appears in the exponent.
As a consequence, all mesons with no orbital angular momentum (L = 0) have odd parity (P = −1).
C-parity[edit]
C-parity is only defined for mesons that are their own antiparticle (i.e. neutral mesons). It represents whether or not the wavefunction of the meson remains the same under the interchange of their quark with their antiquark.[15] If
then, the meson is “C even” (C = +1). On the other hand, if
then the meson is “C odd” (C = −1).
C-parity rarely is studied on its own, but more commonly in combination with P-parity into CP-parity. CP-parity was originally thought to be conserved, but was later found to be violated on rare occasions in weak interactions.[16][17][18]
G-parity[edit]
G-parity is a generalization of the C-parity. Instead of simply comparing the wavefunction after exchanging quarks and antiquarks, it compares the wavefunction after exchanging the meson for the corresponding antimeson, regardless of quark content.[19]
If
then, the meson is “G even” (G = +1). On the other hand, if
then the meson is “G odd” (G = −1).
Isospin and charge[edit]
Combinations of one u, d, or s quark and one u, d, or s antiquark in JP = 0− configuration form a nonet.
Combinations of one u, d, or s quark and one u, d, or s antiquark in JP = 1− configuration also form a nonet.
Original isospin model[edit]
The concept of isospin was first proposed by Werner Heisenberg in 1932 to explain the similarities between protons and neutrons under the strong interaction.[20] Although they had different electric charges, their masses were so similar that physicists believed that they were actually the same particle. The different electric charges were explained as being the result of some unknown excitation similar to spin. This unknown excitation was later dubbed isospin by Eugene Wigner in 1937.[21]
When the first mesons were discovered, they too were seen through the eyes of isospin and so the three pions were believed to be the same particle, but in different isospin states.
The mathematics of isospin was modeled after the mathematics of spin. Isospin projections varied in increments of 1 just like those of spin, and to each projection was associated a “charged state”. Because the “pion particle” had three “charged states”, it was said to be of isospin I = 1 . Its “charged states”
π+
,
π0
, and
π−
, corresponded to the isospin projections I3 = +1 , I3 = 0 , and I3 = −1 respectively. Another example is the “rho particle”, also with three charged states. Its “charged states”
ρ+
,
ρ0
, and
ρ−
, corresponded to the isospin projections I3 = +1 , I3 = 0 , and I3 = −1 respectively.
Replacement by the quark model[edit]
This belief lasted until Murray Gell-Mann proposed the quark model in 1964 (containing originally only the u, d, and s quarks).[22] The success of the isospin model is now understood to be an artifact of the similar masses of the u and d quarks. Because the u and d quarks have similar masses, particles made of the same number of them also have similar masses.
The exact u and d quark composition determines the charge, because u quarks carry charge ++2/3 whereas d quarks carry charge −+1/3. For example, the three pions all have different charges
π+
= (
u
d
)-
π0
= a quantum superposition of (
u
u
) and (
d
d
) states
π−
= (
d
u
)
but they all have similar masses (c. 140 MeV/c2) as they are each composed of a same total number of up and down quarks and antiquarks. Under the isospin model, they were considered a single particle in different charged states.
After the quark model was adopted, physicists noted that the isospin projections were related to the up and down quark content of particles by the relation
where the n -symbols are the count of up and down quarks and antiquarks.
In the “isospin picture”, the three pions and three rhos were thought to be the different states of two particles. However, in the quark model, the rhos are excited states of pions. Isospin, although conveying an inaccurate picture of things, is still used to classify hadrons, leading to unnatural and often confusing nomenclature.
Because mesons are hadrons, the isospin classification is also used for them all, with the quantum number calculated by adding I3 = +1/2 for each positively charged up-or-down quark-or-antiquark (up quarks and down antiquarks), and I3 = −1/2 for each negatively charged up-or-down quark-or-antiquark (up antiquarks and down quarks).
Flavour quantum numbers[edit]
The strangeness quantum number S (not to be confused with spin) was noticed to go up and down along with particle mass. The higher the mass, the lower (more negative) the strangeness (the more s quarks). Particles could be described with isospin projections (related to charge) and strangeness (mass) (see the uds nonet figures). As other quarks were discovered, new quantum numbers were made to have similar description of udc and udb nonets. Because only the u and d mass are similar, this description of particle mass and charge in terms of isospin and flavour quantum numbers only works well for the nonets made of one u, one d and one other quark and breaks down for the other nonets (for example ucb nonet). If the quarks all had the same mass, their behaviour would be called symmetric, because they would all behave in exactly the same way with respect to the strong interaction. However, as quarks do not have the same mass, they do not interact in the same way (exactly like an electron placed in an electric field will accelerate more than a proton placed in the same field because of its lighter mass), and the symmetry is said to be broken.
It was noted that charge (Q) was related to the isospin projection (I3), the baryon number (B) and flavour quantum numbers (S, C, B′, T) by the Gell-Mann–Nishijima formula:[23]
where S, C, B′, and T represent the strangeness, charm, bottomness and topness flavour quantum numbers respectively. They are related to the number of strange, charm, bottom, and top quarks and antiquark according to the relations:
meaning that the Gell-Mann–Nishijima formula is equivalent to the expression of charge in terms of quark content:
Classification[edit]
Mesons are classified into groups according to their isospin (I), total angular momentum (J), parity (P), G-parity (G) or C-parity (C) when applicable, and quark (q) content. The rules for classification are defined by the Particle Data Group, and are rather convoluted.[24] The rules are presented below, in table form for simplicity.
Types of meson[edit]
Mesons are classified into types according to their spin configurations. Some specific configurations are given special names based on the mathematical properties of their spin configuration.
| Type | S | L | P | J | JP |
|---|---|---|---|---|---|
| Pseudoscalar meson | 0 | 0 | − | 0 | 0− |
| Pseudovector meson | 0, 1 | 1 | + | 1 | 1+ |
| Vector meson | 1 | 0, 2 | − | 1 | 1− |
| Scalar meson | 1 | 1 | + | 0 | 0+ |
| Tensor meson | 1 | 1, 3 | + | 2 | 2+ |
Nomenclature[edit]
Flavourless mesons[edit]
Flavourless mesons are mesons made of pair of quark and antiquarks of the same flavour (all their flavour quantum numbers are zero: S = 0, C = 0, B′ = 0, T = 0).[i] The rules for flavourless mesons are:[24]
q q content |
I | JPC [ii] | |||
|---|---|---|---|---|---|
| 0−+, 2−+, 4−+, … | 1+−, 3+−, 5+−, … | 1−−, 2−−, 3−−, … | 0++, 1++, 2++, … | ||
u d  d u |
1 | π+ π0 π− |
b+ b0 b− |
ρ+ ρ0 ρ− |
a+ a0 a− |
| Mix of u u , d d , s s |
0 | η η′ |
h h′ |
ω ϕ |
f f′ |
c c |
0 | η c |
hc | ψ[iii] | χc |
b b |
0 | η b |
hb | ϒ |
χb |
t t |
0 | η t |
ht | θ |
χt |
- ^ For the purpose of nomenclature, the isospin projection I3 is treated as if it were not a flavour quantum number. This means that the charged pion-like mesons (π±, a±, b±, and ρ± mesons) follow the rules of flavourless mesons, even if they aren’t truly “flavourless”.
- ^ C-parity is only relevant for neutral mesons.
- ^ For the special case JPC=1−−, the ψ is called the
J/ψ
- In addition
- When the spectroscopic state of the meson is known, it is added in parentheses.
- When the spectroscopic state is unknown, mass (in MeV/c2) is added in parentheses.
- When the meson is in its ground state, nothing is added in parentheses.
Flavoured mesons[edit]
Flavoured mesons are mesons made of pair of quark and antiquarks of different flavours. The rules are simpler in this case: The main symbol depends on the heavier quark, the superscript depends on the charge, and the subscript (if any) depends on the lighter quark. In table form, they are:[24]
| Quark | Antiquark | |||||
|---|---|---|---|---|---|---|
| up | down | charm | strange | top | bottom | |
| up | — | [i] | D0 |
K+ |
T0 |
B+ |
| down | [i] | — | D− |
K0 |
T− |
B0 |
| charm | D0 |
D+ |
— | D+ s |
T0 c |
B+ c |
| strange | K− |
K0 |
D− s |
— | T− s |
B0 s |
| top | T0 |
T+ |
T0 c |
T+ s |
— | T+ b |
| bottom | B− |
B0 |
B− c |
B0 s |
T− b |
— |
- ^ a b For the purpose of nomenclature, the isospin projection I3 is treated as if it were not a flavour quantum number. This means that the charged pion-like mesons (π±, a±, b±, and ρ± mesons) follow the rules of flavourless mesons, even if they aren’t truly “flavourless”.
- In addition
- If JP is in the “normal series” (i.e., JP = 0+, 1−, 2+, 3−, …), a superscript ∗ is added.
- If the meson is not pseudoscalar (JP = 0−) or vector (JP = 1−), J is added as a subscript.
- When the spectroscopic state of the meson is known, it is added in parentheses.
- When the spectroscopic state is unknown, mass (in MeV/c2) is added in parentheses.
- When the meson is in its ground state, nothing is added in parentheses.
Exotic mesons[edit]
There is experimental evidence for particles that are hadrons (i.e., are composed of quarks) and are color-neutral with zero baryon number, and thus by conventional definition are mesons. Yet, these particles do not consist of a single quark/antiquark pair, as all the other conventional mesons discussed above do. A tentative category for these particles is exotic mesons.
There are at least five exotic meson resonances that have been experimentally confirmed to exist by two or more independent experiments. The most statistically significant of these is the Z(4430), discovered by the Belle experiment in 2007 and confirmed by LHCb in 2014. It is a candidate for being a tetraquark: a particle composed of two quarks and two antiquarks.[26] See the main article above for other particle resonances that are candidates for being exotic mesons.
List[edit]
Pseudoscalar mesons[edit]
| Particle name | Particle symbol |
Antiparticle symbol |
Quark content |
Rest mass (MeV/c2) | IG | JPC | S | C | B’ | Mean lifetime (s) | Commonly decays to (>5% of decays) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pion[27] | π+ |
π− |
u d |
139.57018±0.00035 | 1− | 0− | 0 | 0 | 0 | (2.6033±0.0005)×10−8 | μ+ + ν μ |
| Pion[28] | π0 |
Self |  [a] [a]
|
134.9766±0.0006 | 1− | 0−+ | 0 | 0 | 0 | (8.4±0.6)×10−17 | γ + γ |
| Eta meson[29] | η |
Self |  [a] [a]
|
547.853±0.024 | 0+ | 0−+ | 0 | 0 | 0 | (5.0±0.3)×10−19[b] | γ + γ or π0 + π0 + π0 or π+ + π0 + π− |
| Eta prime meson[30] | η′ (958) |
Self |  [a] [a]
|
957.66±0.24 | 0+ | 0−+ | 0 | 0 | 0 | (3.2±0.2)×10−21[b] | π+ + π− + η or ( ρ0 + γ ) / ( π+ + π− + γ ) or π0 + π0 + η |
| Charmed eta meson[31] | η c(1S) |
Self | c c |
2980.3±1.2 | 0+ | 0−+ | 0 | 0 | 0 | (2.5±0.3)×10−23[b] | See η c decay modes |
| Bottom eta meson[32] | η b(1S) |
Self | b b |
9300±40 | 0+ | 0−+ | 0 | 0 | 0 | Unknown | See η b decay modes |
| Kaon[33] | K+ |
K− |
u s |
493.677±0.016 | 1⁄2 | 0− | 1 | 0 | 0 | (1.2380±0.0021)×10−8 | μ+ + ν μ or
|
| Kaon[34] | K0 |
K0 |
d s |
497.614±0.024 | 1⁄2 | 0− | 1 | 0 | 0 | [c] | [c] |
| K-Short[35] | K0 S |
Self |  [e] [e]
|
497.614±0.024[d] | 1⁄2 | 0− | (*) | 0 | 0 | (8.953±0.005)×10−11 | π+ + π− or π0 + π0 |
| K-Long[36] | K0 L |
Self |  [e] [e]
|
497.614±0.024[d] | 1⁄2 | 0− | (*) | 0 | 0 | (5.116±0.020)×10−8 | π± + e∓ + ν e or π± + μ∓ + ν μ or π0 + π0 + π0 or π+ + π0 + π− |
| D meson[37] | D+ |
D− |
c d |
1869.62±0.20 | 1⁄2 | 0− | 0 | +1 | 0 | (1.040±0.007)×10−12 | See D+ decay modes |
| D meson[38] | D0 |
D0 |
c u |
1864.84±0.17 | 1⁄2 | 0− | 0 | +1 | 0 | (4.101±0.015)×10−13 | See D0 decay modes |
| strange D meson[39] | D+ s |
D− s |
c s |
1968.49±0.34 | 0 | 0− | +1 | +1 | 0 | (5.00±0.07)×10−13 | See D+ s decay modes |
| B meson[40] | B+ |
B− |
u b |
5279.15±0.31 | 1⁄2 | 0− | 0 | 0 | +1 | (1.638±0.011)×10−12 | See B+ decay modes |
| B meson[41] | B0 |
B0 |
d b |
5279.53±33 | 1⁄2 | 0− | 0 | 0 | +1 | (1.530±0.009)×10−12 | See B0 decay modes |
| Strange B meson[42] | B0 s |
B0 s |
s b |
5366.3±0.6 | 0 | 0− | −1 | 0 | +1 | 1.470+0.026 −0.027×10−12 |
See B0 s decay modes |
| Charmed B meson[43] | B+ c |
B− c |
c b |
6276±4 | 0 | 0− | 0 | +1 | +1 | (4.6±0.7)×10−13 | See B+ c decay modes |
[a] ^ Makeup inexact due to non-zero quark masses.
[b] ^ PDG reports the resonance width (Γ). Here the conversion τ = ħ⁄Γ is given instead.
[c] ^ Strong eigenstate. No definite lifetime (see kaon notes below)
[d] ^ The mass of the
K0
L and
K0
S are given as that of the
K0
. However, it is known that a difference between the masses of the
K0
L and
K0
S on the order of 2.2×10−11 MeV/c2 exists.[36]
[e] ^ Weak eigenstate. Makeup is missing small CP–violating term (see notes on neutral kaons below).
Vector mesons[edit]
| Particle name |
Particle symbol |
Antiparticle symbol |
Quark content |
Rest mass (MeV/c2) | IG | JPC | S | C | B’ | Mean lifetime (s) | Commonly decays to (>5% of decays) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Charged rho meson[44] | ρ+ (770) |
ρ− (770) |
u d |
775.4±0.4 | 1+ | 1− | 0 | 0 | 0 | ~4.5×10−24[f][g] | π± + π0 |
| Neutral rho meson[44] | ρ0 (770) |
Self | 
|
775.49±0.34 | 1+ | 1−− | 0 | 0 | 0 | ~4.5×10−24[f][g] | π+ + π− |
| Omega meson[45] | ω (782) |
Self | 
|
782.65±0.12 | 0− | 1−− | 0 | 0 | 0 | (7.75±0.07)×10−23[f] | π+ + π0 + π− or π0 + γ |
| Phi meson[46] | ϕ (1020) |
Self | s s |
1019.445±0.020 | 0− | 1−− | 0 | 0 | 0 | (1.55±0.01)×10−22[f] | K+ + K− or K0 S + K0 L or ( ρ + π ) / ( π+ + π0 + π− ) |
| J/Psi[47] | J/ψ |
Self | c c |
3096.916±0.011 | 0− | 1−− | 0 | 0 | 0 | (7.1±0.2)×10−21[f] | See J/ψ (1S) decay modes |
| Upsilon meson[48] | ϒ (1S) |
Self | b b |
9460.30±0.26 | 0− | 1−− | 0 | 0 | 0 | (1.22±0.03)×10−20[f] | See ϒ (1S) decay modes |
| Kaon[49] | K∗+ |
K∗− |
u s |
891.66±0.026 | 1⁄2 | 1− | 1 | 0 | 0 | ~7.35×10−20[f][g] | See K∗ (892) decay modes |
| Kaon[49] | K∗0 |
K∗0 |
d s |
896.00±0.025 | 1⁄2 | 1− | 1 | 0 | 0 | (7.346±0.002)×10−20[f] | See K∗ (892) decay modes |
| D meson[50] | D∗+ (2010) |
D∗− (2010) |
c d |
2010.27±0.17 | 1⁄2 | 1− | 0 | +1 | 0 | (6.9±1.9)×10−21[f] | D0 + π+ or D+ + π0 |
| D meson[51] | D∗0 (2007) |
D∗0 (2007) |
c u |
2006.97±0.19 | 1⁄2 | 1− | 0 | +1 | 0 | >3.1×10−22[f] | D0 + π0 or D0 + γ |
| strange D meson[52] | D∗+ s |
D∗− s |
c s |
2112.3±0.5 | 0 | 1− | +1 | +1 | 0 | >3.4×10−22[f] | D∗+ + γ or D∗+ + π0 |
| B meson[53] | B∗+ |
B∗− |
u b |
5325.1±0.5 | 1⁄2 | 1− | 0 | 0 | +1 | Unknown | B+ + γ |
| B meson[53] | B∗0 |
B∗0 |
d b |
5325.1±0.5 | 1⁄2 | 1− | 0 | 0 | +1 | Unknown | B0 + γ |
| Strange B meson[54] | B∗0 s |
B∗0 s |
s b |
5412.8±1.3 | 0 | 1− | −1 | 0 | +1 | Unknown | B0 s+ γ |
| Charmed B meson† | B∗+ c |
B∗− c |
c b |
Unknown | 0 | 1− | 0 | +1 | +1 | Unknown | Unknown |
[f] ^ PDG reports the resonance width (Γ). Here the conversion τ = ħ⁄Γ is given instead.
[g] ^ The exact value depends on the method used. See the given reference for detail.
Notes on neutral kaons[edit]
There are two complications with neutral kaons:[55]
- Due to neutral kaon mixing, the
K0
S and
K0
L are not eigenstates of strangeness. However, they are eigenstates of the weak force, which determines how they decay, so these are the particles with definite lifetime. - The linear combinations given in the table for the
K0
S and
K0
L are not exactly correct, since there is a small correction due to CP violation. See CP violation in kaons.
Note that these issues also exist in principle for other neutral, flavored mesons; however, the weak eigenstates are considered separate particles only for kaons because of their dramatically different lifetimes.[55]
See also[edit]
- Mesonic molecule
- Standard Model
Footnotes[edit]
- ^
The ħ is often dropped because it is the “fundamental” unit of spin, and it is implied that “spin 1” means “spin 1 ħ“. In some systems of natural units, ħ is chosen to be 1, and therefore drops out of equations. The remainder of this article uses the “assume ħ units” convention for all types of spin.
References[edit]
- ^ Griffiths, D. (2008). Introduction to Elementary Particles (2nd ed.). Wiley-VCH. ISBN 978-3-527-40601-2.
- ^
Aubert, J.J.; Becker, U.; Biggs, P.; Burger, J.; Chen, M.; Everhart, G.; et al. (1974). “Experimental observation of a Heavy Particle J“. Physical Review Letters. 33 (23): 1404–1406. Bibcode:1974PhRvL..33.1404A. doi:10.1103/PhysRevLett.33.1404. - ^
Augustin, J.E.; Boyarski, A.; Breidenbach, M.; Bulos, F.; Dakin, J.; Feldman, G.; et al. (1974). “Discovery of a narrow resonance in e+e− annihilation”. Physical Review Letters. 33 (23): 1406–1408. Bibcode:1974PhRvL..33.1406A. doi:10.1103/PhysRevLett.33.1406. - ^
Herb, S. W.; Hom, D.; Lederman, L.; Sens, J.; Snyder, H.; Yoh, J.; et al. (1977). “Observation of a di-muon resonance at 9.5 GeV in 400 GeV proton-nucleus collisions”. Physical Review Letters. 39 (5): 252–255. Bibcode:1977PhRvL..39..252H. doi:10.1103/PhysRevLett.39.252. OSTI 1155396. - ^ “Nobel Prize in Physics 1949”. Presentation Speech. The Noble Foundation. 1949.
- ^ Yukawa, H. (1935). “On the Interaction of Elementary Particles” (PDF). Proc. Phys.-Math. Soc. Jpn. 17 (48).
- ^ Yukawa, Hideki (1935). “On the Interaction of Elementary Particles. I”. Nippon Sugaku-Buturigakkwai Kizi Dai 3 Ki. 日本物理学会、日本数学会. 17: 48–57. doi:10.11429/ppmsj1919.17.0_48.
- ^ Gamow, G. (1988) [1961]. The Great Physicists from Galileo to Einstein (Reprint ed.). Dover Publications. p. 315. ISBN 978-0-486-25767-9.
- ^ “D. M. Bose: A Scientist Incognito (editorial)” (PDF). Science and Culture. 76 (11–12). November–December 2010. Retrieved 5 February 2011.
- ^ Lattes, C.; Occhialini, G.; Muirhead, H.; Powell, C. (1947). “Processes involving charged mesons”. Nature. 159: 694–698. doi:10.1007/s00016-014-0128-6. S2CID 122718292.
- ^ Steinberger, J. (1989). “Experiments with high-energy neutrino beams”. Reviews of Modern Physics. 61 (3): 533–545. Bibcode:1989RvMP…61..533S. doi:10.1103/RevModPhys.61.533. PMID 17747881.
- ^ “Particles of the Standard Model”. pdfslide.net. Retrieved 24 May 2020.
- ^
Amsler, C.; et al. (Particle Data Group) (2008). “Quark Model” (PDF). Reviews. Lawrence Berkeley Laboratory. - ^
Amsler, C.; et al. (Particle Data Group) (2008). “Review of Particle Physics” (PDF). Physics Letters B. 667 (1): 1–1340. Bibcode:2008PhLB..667….1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. PMID 10020536. S2CID 227119789. - ^ Sozzi, M. S. (2008b). “Charge Conjugation”. Discrete Symmetries and CP Violation: From Experiment to Theory. Oxford University Press. pp. 88–120. ISBN 978-0-19-929666-8.
- ^ Cronin, J.W. (1980). “CP Symmetry Violation—The Search for its origin” (PDF). The Nobel Foundation.
- ^ Fitch, V.L. (1980). “The Discovery of Charge—Conjugation Parity Asymmetry” (PDF). The Nobel Foundation.
- ^ Sozzi, M. S. (2008c). “CP-Symmetry”. Discrete Symmetries and CP Violation: From Experiment to Theory. Oxford University Press. pp. 231–275. ISBN 978-0-19-929666-8.
- ^ Gottfried, K.; Weisskopf, V.F. (1986). “Hadronic spectroscopy: G-parity”. Concepts of Particle Physics. Vol. 2. Oxford University Press. pp. 303–311. ISBN 0-19-503393-0.
- ^ Heisenberg, W. (1932). “Über den Bau der Atomkerne”. Zeitschrift für Physik (in German). 77 (1–2): 1–11. Bibcode:1932ZPhy…77….1H. doi:10.1007/BF01342433. S2CID 186218053.
- ^ Wigner, E. (1937). “On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei”. Physical Review. 51 (2): 106–119. Bibcode:1937PhRv…51..106W. doi:10.1103/PhysRev.51.106.
- ^ Gell-Mann, M. (1964). “A Schematic of Baryons and Mesons”. Physics Letters. 8 (3): 214–215. Bibcode:1964PhL…..8..214G. doi:10.1016/S0031-9163(64)92001-3.
- ^ Wong, S.S.M. (1998). “Nucleon Structure”. Introductory Nuclear Physics (2nd ed.). New York: John Wiley & Sons. pp. 21–56. ISBN 0-471-23973-9.
- ^ a b c
Amsler, C.; et al. (Particle Data Group) (2008). “Naming scheme for hadrons” (PDF). Reviews. Lawrence Berkeley Laboratory. - ^ Burcham, W. E.; Jobes, M. (1995). Nuclear and Particle Physics (2nd ed.). Longman Publishing. ISBN 0-582-45088-8.
- ^ LHCb collaborators (2014): Observation of the resonant character of the Z(4430)− state
- ^ C. Amsler et al. (2008): Particle listings –
π±
- ^ C. Amsler et al. (2008): Particle listings –
π0
- ^ C. Amsler et al. (2008): Particle listings –
η
- ^ C. Amsler et al. (2008): Particle listings –
η′
- ^ C. Amsler et al. (2008): Particle listings –
η
c - ^ C. Amsler et al. (2008): Particle listings –
η
b - ^ C. Amsler et al. (2008): Particle listings –
K±
- ^ C. Amsler et al. (2008): Particle listings –
K0
- ^ C. Amsler et al. (2008): Particle listings –
K0
S - ^ a b C. Amsler et al. (2008): Particle listings –
K0
L - ^ C. Amsler et al. (2008): Particle listings –
D±
- ^ C. Amsler et al. (2008): Particle listings –
D0
- ^ C. Amsler et al. (2008): Particle listings –
D±
s - ^ C. Amsler et al. (2008): Particle listings –
B±
- ^ C. Amsler et al. (2008): Particle listings –
B0
- ^ C. Amsler et al. (2008): Particle listings –
B0
s - ^ C. Amsler et al. (2008): Particle listings –
B±
c - ^ a b C. Amsler et al. (2008): Particle listings –
ρ
- ^ C. Amsler et al. (2008): Particle listings –
ω
(782) - ^ C. Amsler et al. (2008): Particle listings –
ϕ
- ^ C. Amsler et al. (2008): Particle listings – J/Ψ
- ^ C. Amsler et al. (2008): Particle listings –
ϒ
(1S) - ^ a b C. Amsler et al. (2008): Particle listings –
K∗
(892) - ^ C. Amsler et al. (2008): Particle listings –
D∗±
(2010) - ^ C. Amsler et al. (2008): Particle listings –
D∗0
(2007) - ^ C. Amsler et al. (2008): Particle listings –
D∗±
s - ^ a b C. Amsler et al. (2008): Particle listings –
B∗
- ^ C. Amsler et al. (2008): Particle listings –
B∗
s - ^ a b J.W. Cronin (1980)
External links[edit]
- Nave, C.R., ed. (2005). “A table of some mesons and their properties”. Department of Physics and Astronomy. Hyperphysics. Atlanta, GA: Georgia State University.
- “Particle Data Group”. Lawrence Berkeley Laboratory (main page). Lawrence, CA. — Compiles authoritative information on particle properties
- van Beveren, Eef; Rupp, George; Petropoulos, Nicholas; Kleefeld, Frieder (2003) [26 Nov 2002]. “The light scalar mesons within quark models”. American Institute of Physics Conference Proceedings. 660: 353–366. arXiv:hep-ph/0211411. Bibcode:2003AIPC..660..353V. doi:10.1063/1.1570585. S2CID 6295609.
- “Naming scheme for hadrons” (PDF). Particle Data Group. Lawrence, CA: Lawrence Berkeley Laboratory. 2004.
- “Mesons made thinkable”. thingsmadethinkable.com. — An interactive visualisation allowing physical properties to be compared
- Perricone, Mike (22 March 2006). “What happened to the antimatter? Fermilab’s DZero experiment finds clues in quick-change meson” (Press release). Batavia, IL: Fermi National Accelerator Laboratory (Fermilab).
- Perricone, Mike (25 September 2006). “Fermilab’s CDF scientists make it official: They have discovered the quick-change behavior of the B-sub-s meson, which switches between matter and antimatter 3 trillion times a second” (Press release). Batavia, IL: Fermi National Accelerator Laboratory (Fermilab).
Увеличить/уменьшить масштаб
Скопировать текст страницы
(работает в Chrome 42+,
Microsoft Internet Explorer и Mozilla FireFox
c установленным Adobe Flash Player)
Текущие страницы выделены рамкой.
Содержание
Обращаясь к сайту «История Росатома — Электронная библиотека»,
я соглашаюсь с условиями использования представленных там материалов.
Правила сайта (далее – Правила)
- Общие положения
- Настоящие правила определяют порядок и условия использования материалов, размещенных на сайте www.biblioatom.ru (далее именуется Сайт), а также правила использования материалов Сайтом и порядок
взаимодействия с Администрацией Сайта. - Любые материалы, размещенные на Сайте, являются объектами интеллектуальной собственности (объектами авторского права или смежных прав, а также прав на средства индивидуализации). Права Администрации
Сайта на указанные материалы охраняются законодательством о правах на результаты интеллектуальной деятельности. - Использование материалов, размещенных на Сайте, допускается только с письменного согласия Администрации Сайта или иного правообладателя, прямо указанного на конкретном материале, размещенном на
Сайте, или в непосредственной близости от указанного материала. - Права на использование и разрешение использования материалов, размещенных на Сайте, принадлежащих иным правообладателям, нежели Администрация Сайта, допускается с разрешения таких правообладателей
или в соответствии с условиями, установленными такими правообладателями. Никакое из положений настоящих Правил не дает прав третьим лицам на использование материалов правообладателей, прямо указанных на
конкретном материале, размещенном на Сайте, или в непосредственной близости от указанного материала. - Настоящие Правила распространяют свое действие на следующих пользователей: информационные агентства, электронные и печатные средства массовой информации, любые физические и юридические лица, а также
индивидуальные предприниматели (далее — «Пользователи»).
- Настоящие правила определяют порядок и условия использования материалов, размещенных на сайте www.biblioatom.ru (далее именуется Сайт), а также правила использования материалов Сайтом и порядок
- Использование материалов. Виды использования
- Под использованием материалов Сайта понимается воспроизведение, распространение, публичный показ, сообщение в эфир, сообщение по кабелю, перевод, переработка, доведение до всеобщего сведения и иные
способы использования, предусмотренные действующим законодательством Российской Федерации. - Использование материалов Сайта без получения разрешения от Администрации Сайта не допустимо.
- Внесение каких-либо изменений и/или дополнений в материалы Сайта запрещено.
- Использование материалов Сайта осуществляется на основании договоров с Администрацией Сайта, заключенных в письменной форме, или на основании письменного разрешения, выданного Администрацией Сайта.
- Запрещается любое использование (бездоговорное/без разрешения) фото-, графических, видео-, аудио- и иных материалов, размещенных на Сайте, принадлежащих Администрации Сайта и иным правообладателям
(третьим лицам). - Стоимость использования каждого конкретного материала или выдача разрешения на его использование согласуется Пользователем и Администрацией Сайта в каждом конкретном случае.
- В случае необходимости использования материалов Сайта, права на которые принадлежат третьим лицам (иным правообладателям, нежели Администрация Сайта, о чем прямо указано на таких материалах либо в
непосредственной близости от них), Пользователи обязаны обращаться к правообладателям таких материалов для получения разрешения на использование материалов.
- Под использованием материалов Сайта понимается воспроизведение, распространение, публичный показ, сообщение в эфир, сообщение по кабелю, перевод, переработка, доведение до всеобщего сведения и иные
- Обязанности Пользователей при использовании материалов Сайта
- 3.1. При использовании материалов Сайта в любых целях при наличии разрешения Администрации Сайта, ссылка на Сайт обязательна и осуществляется в следующем виде:
- в печатных изданиях или в иных формах на материальных носителях Пользователи обязаны в каждом случае использования материалов указать источник – электронная библиотека «История Росатома»
(www.biblioatom.ru) - в интернете или иных формах использования в электронном виде не на материальных носителях, Пользователи в каждом случае использования материалов обязаны разместить гиперссылку на Сайт —
электронная
библиотека «История Росатома» (www.biblioatom.ru), гиперссылка должна являться активной и прямой, при нажатии на которую Пользователь переходит на конкретную страницу Сайта, с которой заимствован
материал. - Ссылка на источник или гиперссылка, указанные в пп. 3.1.1 и 3.1.2. настоящих Правил, должны быть помещены Пользователем в начале используемого текстового материала, а также непосредственно
под используемым аудио-, видео-, фотоматериалом, графическим материалом Администрации Сайта.
- в печатных изданиях или в иных формах на материальных носителях Пользователи обязаны в каждом случае использования материалов указать источник – электронная библиотека «История Росатома»
- Размеры шрифта ссылки на источник или гиперссылки не должны быть меньше размера шрифта текста, в котором используются материалы Сайта, либо размера шрифта текста Пользователя, сопровождающего аудио-,
видео-, фотоматериалы и графические материалы Сайта, а также цвет ссылки должен быть идентичен цветам ссылок на Сайте и должен быть видимым Пользователю. - Использование материалов с Сайта, полученных из вторичных источников (от иных правообладателей, нежели Администрация Сайта, о чем прямо указано на таких материалах либо в непосредственной близости от
них), возможно только со ссылкой на эти источники и, в случае необходимости, установленной такими источниками (правообладателями), — с их разрешения. - Не допускается переработка оригинального материала (произведения), взятого с Сайта, в том числе сокращение материала, иная его переработка, в том числе приводящая к искажению его смысла.
- 3.1. При использовании материалов Сайта в любых целях при наличии разрешения Администрации Сайта, ссылка на Сайт обязательна и осуществляется в следующем виде:
- Права на материалы третьих лиц, урегулирование претензий
- Материалы, права на которые принадлежат третьим лицам, размещенные на Сайте, размещены либо с разрешения правообладателя, полученного Администрацией Сайта, либо, в случае, если таковое использование
прямо не запрещено правообладателем, в соответствии с Законодательством РФ в информационных целях с обязательным указанием имени автора, материал которого используется, и источника заимствования. - В случае, если в обозначении авторства материалов в соответствии с п. 4.1. настоящих Правил содержится ошибка, или в случае использования материала с предполагаемым или реальным нарушением прав
третьих лиц, или в иных спорных случаях использования объектов интеллектуальной собственности, размещенных на Сайте, в том числе в случае, когда права третьего лица тем или иным образом нарушаются с
использованием Сайта, применяется следующая схема урегулирования претензий третьих лиц к Администрации Сайта:- в адрес Администрации Сайта по электронной почте на адрес info@biblioatom.ru направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
принадлежат
заявителю и который используется незаконно посредством Сайта или с нарушением правил использования, или иным образом права заявителя как обладателя исключительного права на объект интеллектуальной
собственности, размещенный на Сайте, нарушены посредством Сайта, с приложением документов, подтверждающих правомочия заявителя, данные о правообладателе и копия доверенности на действия от лица
правообладателя, если лицо, направляющее претензию, не является руководителем компании правообладателя или непосредственно физическим лицом — правообладателем. В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав; - Администрация Сайта обязуется рассмотреть надлежаще оформленную претензию в срок не менее 5 (пяти) рабочих дней с даты ее получения по электронной почте. Администрация Сайта обязуется
уведомить
заявителя о результатах рассмотрения его заявления (претензии) посредством отправки письма по электронной почте на адрес, указанный заявителем, а также направить ответ в письменном виде на адрес,
указанный заявителем (в случае неуказания такового адреса отправки, обязательство по предоставлению письменного ответа на претензию с Администрации Сайта снимается). В том числе, Администрация
Сайта
вправе запросить дополнительные документы, свидетельства, данные, подтверждающие законность предъявляемой претензии. В случае признания претензии правомерной, Администрация Сайта примет все
возможные
меры, необходимые для прекращения нарушения прав заявителя и урегулирования претензии; - Администрация Сайта в любом случае предпринимает все возможные меры к скорейшему удовлетворению обоснованных претензий третьих лиц и стремиться к максимально скорому урегулированию всех
спорных
вопросов.
- в адрес Администрации Сайта по электронной почте на адрес info@biblioatom.ru направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
- Материалы, права на которые принадлежат третьим лицам, размещенные на Сайте, размещены либо с разрешения правообладателя, полученного Администрацией Сайта, либо, в случае, если таковое использование
- Прочие условия
- Администрация Сайта оставляет за собой право изменять настоящие Правила в одностороннем порядке в любое время без уведомления Пользователей. Любые изменения будут размещены на Сайте. Изменения
вступают в силу с момента их опубликования на Сайте. - По всем вопросам использования материалов Сайта Пользователи могут обращаться к Администрации Сайта по следующим координатам: info@biblioatom.ru
- Во всем, что не урегулировано настоящими Правилами в отношении вопросов использования материалов на Сайте, стороны руководствуются положениями Законодательства РФ.
- Администрация Сайта оставляет за собой право изменять настоящие Правила в одностороннем порядке в любое время без уведомления Пользователей. Любые изменения будут размещены на Сайте. Изменения
Субатомная частица; состоит из равного количества кварков и антикварков
 |
|
| Состав | Состав – Кварки и антикварки |
|---|---|
| Статистика | Бозонные |
| Взаимодействия | Сильный, Слабый, Электромагнитный и Гравитация |
| Теоретически | Хидеки Юкава (1935) |
| Обнаружен | 1947 |
| Типы | ~ 140 (Список ) |
| Масса | От 134,9 МэВ / c (. π. ). до 9,460 ГэВ / c (. ϒ. ) |
| Электрический заряд | – 1 e, 0 e, +1 e |
| Spin | 0, 1 |
В физике элементарных частиц, мезоны (или ) – это адронные субатомные частицы, состоящие из одного кварка и одного антикварка, связанных вместе сильными взаимодействиями. Поскольку мезоны состоят из кварковых субчастиц, они имеют значимый физический размер, диаметр примерно в один фемтометр (1 × 10 м), что составляет примерно в 1,2 раза больше размера протона или нейтрона. Все мезоны нестабильны, с самыми долгоживущими las всего на несколько сотых микросекунды. Заряженные мезоны распадаются (иногда через посредствующие частицы) с образованием электронов и нейтрино. Незаряженные мезоны могут распадаться на фотоны. Оба эти затухания означают, что цвет больше не является свойством побочных продуктов.
Вне ядра мезоны появляются в природе только как короткоживущие продукты столкновений очень высоких энергий между частицами, состоящими из кварков, например космические лучи (протоны и нейтроны высоких энергий) и барионная материя. Мезоны часто создаются искусственно в циклотроне при столкновениях протонов, антипротонов или других частиц.
Мезоны более высоких энергий (более массивные) были созданы на мгновение во время Большого взрыва, но, как считается, сегодня они не играют роли в природе. Однако такие тяжелые мезоны регулярно создаются в экспериментах на ускорителе частиц , чтобы понять природу более тяжелых типов кварков, из которых состоят более тяжелые мезоны.
Мезоны являются частью семейства адронных частиц и определяются просто как частицы, состоящие из четного числа кварков. Другими членами семейства адронов являются барионы : субатомные частицы, состоящие из нечетного числа валентных кварков (по крайней мере, 3), и некоторые эксперименты показывают доказательства экзотических мезонов, которые не имеют обычное валентное кварковое содержание двух кварков (один кварк и один антикварк), но 4 или более.
Поскольку кварки имеют спин 1/2, разница в количестве кварков между мезонами и барионами приводит к тому, что обычные двухкварковые мезоны являются бозонами, тогда как барионы являются фермионами.
Каждому типу мезонов соответствует античастица (антимезон), в которой кварки заменены соответствующими им антикварками, и наоборот. Например, положительный пион (. π.) состоит из одного верхнего кварка и одного нижнего антикварка; и соответствующая ему античастица, отрицательный пион (. π.), состоит из одного верхнего антикварка и одного нижнего кварка.
Поскольку мезоны состоят из кварков, они участвуют как в слабом, так и в сильном взаимодействиях. Мезоны с чистым электрическим зарядом также участвуют в электромагнитном взаимодействии. Мезоны классифицируются в соответствии с их кварковым содержанием, полным угловым моментом, четностью и различными другими свойствами, такими как C-четность и G-четность. Хотя ни один из мезонов не является стабильным, мезоны с меньшей массой , тем не менее, более стабильны, чем более массивные, и, следовательно, их легче наблюдать и изучать на ускорителях частиц или в космических лучах эксперименты. Мезоны также обычно менее массивны, чем барионы, а это означает, что они легче производятся в экспериментах и, таким образом, демонстрируют определенные явления с более высокими энергиями легче, чем барионы. Например, очарованный кварк был впервые обнаружен в мезоне J / Psi (. J / ψ.) в 1974 году, а нижний кварк в ипсилон-мезон (. ϒ.) в 1977 г.
Содержание
- 1 История
- 2 Обзор
- 2.1 Спин, орбитальный угловой момент и полный угловой момент
- 2.2 Четность
- 2.3 C- четность
- 2.4 G-четность
- 2.5 Изоспин и заряд
- 2.6 Квантовые числа аромата
- 3 Классификация
- 3.1 Типы мезонов
- 3.2 Номенклатура
- 3.2.1 Мезоны без запаха
- 3.2.2 Ароматизированные мезоны
- 4 Экзотические мезоны
- 5 Список
- 5.1 Псевдоскалярные мезоны
- 5.2 Векторные мезоны
- 5.3 Примечания к нейтральным каонам
- 6 См. Также
- 7 Примечания
- 8 Ссылки
- 9 Внешние ссылки
- 9.1 Недавние открытия
История
Из теоретических соображений в 1934 г. Хидеки Юкава предсказал существование и приблизительную массу «мезона». как носитель ядерной силы, которая удерживает вместе атомные ядра. Если бы не было ядерной силы, все ядра с двумя или более протонами разлетелись бы из-за электромагнитного отталкивания. Юкава назвал свою частицу-носитель мезон, от μέσος mesos, греческого слова, обозначающего «промежуточный», потому что его предсказанная масса была между массой электрона и протона, масса которого примерно в 1836 раз больше массы тела. электрон. Юкава или Карл Дэвид Андерсон, открывший мюон, первоначально назвал частицу «мезотроном», но его поправил физик Вернер Гейзенберг (чей отец был профессором греческого языка в Мюнхенском университете ). Гейзенберг указал, что в греческом слове «мезос» нет «tr».
Первый кандидат в мезон Юкавы, ныне известный в современной терминологии как мюон, был открыт в 1936 году. Автор Карл Дэвид Андерсон и другие в продуктах распада взаимодействий космических лучей. Мю-мезон имел примерно подходящую массу, чтобы быть носителем сильного ядерного взаимодействия Юкавы, но в течение следующего десятилетия стало очевидно, что это не та частица. В конце концов было обнаружено, что «мю-мезон» вообще не участвует в сильном ядерном взаимодействии, а скорее ведет себя как тяжелая версия электрона, и в конечном итоге был классифицирован как лептон вроде электрон, а не мезон. Физики, делая этот выбор, решили, что классификация частиц должна определяться свойствами, отличными от массы частицы.
Были годы задержки в исследованиях субатомных частиц во время Второй мировой войны (1939–1945), когда большинство физиков работали над прикладными проектами для нужд военного времени. Когда в августе 1945 года закончилась война, многие физики постепенно вернулись к мирным исследованиям. Первый истинный мезон, который был обнаружен, был позже назван “пи-мезон ” (или пион). Это открытие было сделано в 1947 году Сесилом Пауэллом, Сезаром Латтес и Джузеппе Оккиалини, которые исследовали продукты космических лучей в Бристольском университете. в Англии на основе фотопленок, размещенных в Андах. Некоторые из этих мезонов имели примерно ту же массу, что и уже известный мю-мезон, но, казалось, распадались на него, что привело физика Роберта Маршака к гипотезе в 1947 году, что это был действительно новый и другой мезон. В течение следующих нескольких лет новые эксперименты показали, что пион действительно участвует в сильных взаимодействиях. Пион (как виртуальная частица ) также считается основным переносчиком силы ядерной силы в атомных ядрах. Другие мезоны, такие как виртуальные ро-мезоны, также участвуют в передаче этой силы, но в меньшей степени. После открытия пиона Юкава был награжден 1949 Нобелевской премией по физике за свои предсказания.
В прошлом слово мезон иногда использовалось для обозначения любого носителя силы, например “Z-мезон”, который участвует в слабом взаимодействии. Однако такое использование перестало быть популярным, и теперь мезоны определяются как частицы, состоящие из пар кварков и антикварков.
Обзор
Спин, орбитальный угловой момент и полный угловой момент
Спин (квантовое число S) – это векторная величина, которая представляет «внутреннюю “угловой момент частицы. Он идет с шагом 1/2 ħ. Ħ часто опускается, потому что это «основная» единица вращения, и подразумевается, что «спин 1» означает «спин 1 ħ». (В некоторых системах натуральных единиц, выбрано равным 1 и поэтому не фигурирует в уравнениях.)
Кварки – это фермионы – в частности, в этом случае, частицы со спином 1/2 (S = 1/2). Поскольку проекции спина изменяются с шагом 1 (то есть 1), отдельный кварк имеет вектор спина длиной 1/2 и две проекции спина (S z = +1/2 и S z = – + 1/2). Спины двух кварков могут быть выровнены, и в этом случае два вектора спина складываются, чтобы получить вектор длины S = 1 и три проекции спина (S z = +1, S z = 0 и S z = −1), называемый триплетом. Если два кварка имеют невыровненные спины, векторы спина складываются, чтобы получить вектор длины S = 0 и только одну проекцию спина (S z = 0), называемую синглетом. Поскольку мезоны состоят из одного кварка и одного антикварка, их можно найти в триплетных и синглетных спиновых состояниях. Последние называются скалярными мезонами или псевдоскалярными мезонами в зависимости от их четности (см. Ниже).
Существует еще одна величина квантованного углового момента, называемая орбитальным угловым моментом (квантовое число L), то есть угловой момент, возникающий из-за кварков, вращающихся вокруг друг друга, и приходит с шагом 1 час. Полный угловой момент (квантовое число J) частицы представляет собой комбинацию собственного углового момента (спина) и орбитального углового момента. Может принимать любое значение из J = | L – S | до J = | L + S | с шагом 1.
| S | L | J | P | J |
|---|---|---|---|---|
| 0 | 0 | 0 | − | 0 |
| 1 | 1 | + | 1 | |
| 2 | 2 | − | 2 | |
| 3 | 3 | + | 3 | |
| 1 | 0 | 1 | − | 1 |
| 1 | 2, 1, 0 | + | 2, 1, 0 | |
| 2 | 3, 2, 1 | − | 3, 2, 1 | |
| 3 | 4, 3, 2 | + | 4, 3, 2 |
Физиков элементарных частиц больше всего интересуют мезоны без орбитального углового момента (L = 0), поэтому две наиболее изученные группы мезонов: S = 1; L = 0 и S = 0; L = 0, что соответствует J = 1 и J = 0, хотя они не единственные. Также возможно получить частицы J = 1 из S = 0 и L = 1. Как различать мезоны S = 1, L = 0 и S = 0, L = 1 – активная область исследований в мезонная спектроскопия.
Четность
Если бы Вселенная отражалась в зеркале, большинство законов физики были бы идентичны – вещи вели бы себя одинаково, независимо от того, что мы называем «левым» и тем, что мы называем «правым». Эта концепция зеркального отражения называется четностью (P). Гравитация, электромагнитная сила и сильное взаимодействие – все они ведут себя одинаково, независимо от того, отражается ли Вселенная в зеркале или нет, и, следовательно, сказал сохранить четность (P-симметрия). Однако слабое взаимодействие действительно отличает «левое» от «правого», явление, называемое нарушением четности (P-нарушение).
Исходя из этого, можно было бы подумать, что если бы волновая функция для каждой частицы (точнее, квантовое поле для каждого типа частицы) одновременно зеркально перевернула, то новый набор волновых функций полностью удовлетворял бы законам физики (за исключением слабого взаимодействия). Оказывается, это не совсем так: для того, чтобы уравнения были удовлетворены, волновые функции определенных типов частиц должны быть умножены на -1, в дополнение к зеркальному обращению. Говорят, что такие типы частиц имеют отрицательную или нечетную четность (P = -1 или, альтернативно, P = -), тогда как другие частицы говорят, что имеют положительную или четную четность (P = +1 или, альтернативно, P = +).
Для мезонов четность связана с орбитальным угловым моментом соотношением:
- P = (- 1) L + 1 { displaystyle P = left (-1 right) ^ {L + 1}}
, где L является результатом четности соответствующей сферической гармоники волновой функции . «+1» происходит из-за того, что согласно уравнению Дирака кварк и антикварк имеют противоположные внутренние четности. Следовательно, внутренняя четность мезона – это произведение внутренних четностей кварка (+1) и антикварка (−1). Поскольку они разные, их произведение равно -1, и поэтому он дает «+1», который появляется в экспоненте.
Как следствие, все мезоны без орбитального углового момента (L = 0) имеют нечетную четность (P = −1).
C-четность
C-четность определяется только для мезонов, которые являются их собственными античастицами (т.е. нейтральные мезоны). Он показывает, остается ли волновая функция мезона той же самой при обмене их кварком с их антикварком. Если
- | q q ¯⟩ = | q ¯ q⟩ { displaystyle | q { bar {q}} rangle = | { bar {q}} q rangle}
тогда мезон является “четным C” (C = +1). С другой стороны, если
- | q q ¯⟩ = – | q ¯ q⟩ { displaystyle | q { bar {q}} rangle = – | { bar {q}} q rangle}
тогда мезон “C нечетный” (C = −1).
C-четность редко изучается сама по себе, но чаще в сочетании с P-четностью в CP-четность. Считалось, что CP-четность сохраняется, но позже было обнаружено, что она нарушается в слабых взаимодействиях.
G-четность
G-четность является обобщением C-четности. Вместо простого сравнения волновой функции после обмена кварками и антикварками, он сравнивает волновую функцию после обмена мезона на соответствующий антимезон, независимо от содержания кварков.
Если
- | q 1 q ¯ 2⟩ = | q ¯ 1 q 2⟩ { displaystyle | q_ {1} { bar {q}} _ {2} rangle = | { bar {q}} _ {1} q_ {2} rangle}
тогда мезон является «четным G» (G = +1). С другой стороны, если
- | q 1 q ¯ 2⟩ = – | q ¯ 1 q 2⟩ { displaystyle | q_ {1} { bar {q}} _ {2} rangle = – | { bar {q}} _ {1} q_ {2} rangle}
тогда мезон является «G нечетным» (G = −1).
Изоспин и заряд


Концепция изоспина была впервые предложена Вернером Гейзенбергом в 1932 году для объяснения сходства между протонами и нейтроны при сильном взаимодействии. Хотя у них были разные электрические заряды, их массы были настолько похожи, что физики считали, что на самом деле это одна и та же частица. Различные электрические заряды объяснялись как результат какого-то неизвестного возбуждения, подобного спину. Это неизвестное возбуждение было позже названо изоспином Юджином Вигнером в 1937 году. Когда были открыты первые мезоны, они тоже были видны глазами изоспина, поэтому три пиона считались одной и той же частицей, но в различные изоспиновые состояния.
Эта вера сохранялась до тех пор, пока Мюррей Гелл-Манн не предложил кварковую модель в 1964 году (первоначально содержащую только кварки u, d и s). Успех изоспиновой модели теперь понимается как результат схожести масс u- и d-кварков. Поскольку u- и d-кварки имеют схожие массы, частицы, состоящие из одного и того же количества кварков, также имеют схожие массы. Точный конкретный состав u- и d-кварков определяет заряд, потому что u-кварки несут заряд ++ 2/3, тогда как d-кварки несут заряд – + 1/3. Например, все три пиона имеют разные заряды (. π. (. u.. d.),. π. (квантовая суперпозиция состояний. u.. u. и. d.. d.),. π. (. d.. u.)), но имеют схожие массы (около 140 МэВ / c), поскольку каждая из них состоит из одинакового общего числа верхних и нижних кварков и антикварков. В рамках модели изоспина они считались одной частицей в разных заряженных состояниях.
Математика изоспина была смоделирована после математики спина. Проекции изоспина изменялись с шагом 1, как и проекции спина, и с каждой проекцией было связано «заряженное состояние ». Поскольку «пионная частица» имела три «заряженных состояния», было сказано, что она имеет изоспин I = 1. Ее «заряженные состояния». π.,. π. и. π. соответствуют проекциям изоспина I 3 = +1, I 3 = 0 и I 3 = -1 соответственно. Другой пример – «ро-частица », также с тремя заряженными состояниями. Его “заряженные состояния”. ρ.,. ρ. и. ρ. соответствуют проекциям изоспина I 3 = +1, I 3 = 0 и I 3 = −1 соответственно. Позже было отмечено, что проекции изоспина были связаны с верхним и нижним содержанием кварков в частицах соотношением
- I 3 = 1 2 [(nu – nu ¯) – (nd – nd ¯)], { displaystyle I_ {3} = { frac {1} {2}} [(n_ {u} -n _ { bar {u}}) – (n_ {d} -n _ { bar {d}})],}
, где n – количество верхних и нижних кварков и антикварков.
В «изоспиновой картине» три пиона и три rhos считались разными состояниями двух частиц. Однако в кварковой модели rhos представляют собой возбужденные состояния пионов. Изоспин, хотя и передает неточную картину вещей, по-прежнему используется для классификации адронов, что приводит к неестественной и часто сбивающей с толку номенклатуре. Поскольку мезоны являются адронами, также используется изоспиновая классификация: I 3 = ++ 1/2 для восходящих кварков и нижних антикварков, и I 3 = – + 1/2 для вверх антикварки и вниз кварки.
Квантовые числа аромата
Было замечено, что странность квантовое число S (не путать со спином) поднимается и опускается вместе с частицей масса. Чем больше масса, тем меньше странность (тем больше s-кварков). Частицы могут быть описаны с помощью проекций изоспина (связанных с зарядом) и странности (массы) (см. Рисунки uds nonet). Когда были открыты другие кварки, были созданы новые квантовые числа, описывающие udc и udb нонеты аналогично. Поскольку только массы u и d похожи, это описание массы и заряда частицы в терминах изоспина и квантовых чисел аромата хорошо работает только для нонетов, состоящих из одного кварка u, одного d и одного другого кварка, и распадается для других нонетов ( например ucb nonet). Если бы все кварки имели одинаковую массу, их поведение было бы названо симметричным, потому что все они вели бы себя одинаково в отношении сильного взаимодействия. Однако, поскольку кварки не имеют одинаковой массы, они не взаимодействуют одинаково (точно так же, как электрон, помещенный в электрическое поле, будет ускоряться больше, чем протон, помещенный в то же поле, из-за своей более легкой массы), а симметрия считается сломанным.
Было отмечено, что заряд (Q) был связан с проекцией изоспина (I 3), барионным числом (B) и ароматом квантовые числа (S, C, B ′, T) по формуле Гелл-Манна – Нисиджимы :
- Q = I 3 + 1 2 (B + S + C + B ′ + T), { displaystyle Q = I_ {3} + { frac {1} {2}} (B + S + C + B ^ { prime} + T),}
где S, C, B ‘и T представляют странность, очарование, низость и верховность квантовые числа аромата соответственно. Они связаны с количеством странных, очаровательных, нижних и верхних кварков и антикварков согласно соотношениям:
- S = – (ns – ns ¯) { displaystyle S = – (n_ {s} -n _ { bar {s}})}
- C = + (nc – nc ¯) { displaystyle C = + (n_ {c} -n _ { bar {c}})}
- B ′ = – (nb – nb ¯) { displaystyle B ^ { prime} = – (n_ {b} -n _ { bar {b}})}
- T = + (nt – nt ¯), { displaystyle T = + (n_ {t} -n _ { bar {t}}),}
означает, что формула Гелл-Манна – Нишиджима эквивалентна выражению заряда в терминах кваркового содержания:
- Q = 2 3 [ (nu – nu ¯) + (nc – nc ¯) + (nt – nt ¯)] – 1 3 [(nd – nd ¯) + (ns – ns ¯) + (nb – nb ¯)]. { displaystyle Q = { frac {2} {3}} [(n_ {u} -n _ { bar {u}}) + (n_ {c} -n _ { bar {c}}) + (n_ {t} -n _ { bar {t}})] – { frac {1} {3}} [(n_ {d} -n _ { bar {d}}) + (n_ {s} -n_ { bar {s}}) + (n_ {b} -n _ { bar {b}})].}
Классификация
Мезоны делятся на группы в соответствии с их изоспином (I), полный угловой момент (Дж), четность (P), G-четность (G) или C-четность (C), если применимо, и содержимое кварка (q). Правила классификации определены Группой данных о частицах и довольно запутаны. Правила представлены ниже в виде таблицы для простоты.
Типы мезонов
Мезоны подразделяются на типы в соответствии с их спиновой конфигурацией. Некоторым конкретным конфигурациям даны специальные имена, основанные на математических свойствах их спиновой конфигурации.
| Тип | S | L | P | J | J |
|---|---|---|---|---|---|
| Псевдоскалярный мезон | 0 | 0 | − | 0 | 0 |
| Псевдовекторный мезон | 0, 1 | 1 | + | 1 | 1 |
| Векторный мезон | 1 | 0, 2 | − | 1 | 1 |
| Скалярный мезон | 0 | 1 | + | 0 | 0 |
| 1 | 1, 3 | + | 2 | 2 |
Номенклатура
Мезоны без запаха
Мезоны без запаха – это мезоны, состоящие из пары кварков и антикварков одного аромата (все их квантовые числа аромата равны нулю: S = 0, C = 0, B ′ = 0, T = 0). Правила для мезонов без запаха:
| . q.. q. содержание | J | I | |||
|---|---|---|---|---|---|
| 0, 2, 4,… | 1, 3, 5,… | 1, 2, 3,… | 0, 1, 2,… | ||
. u.. d.. uu ¯ – dd ¯ 2 { displaystyle mathrm { tfrac {u { bar {u}) } -d { bar {d}}} { sqrt {2}}}} .. d.. u. .. d.. u. |
1 | . π.. . π.. . π. | b. b. b | . ρ.. . ρ.. . ρ. | a. a. a |
| Смесь. u.. u.,. d.. d.,. s.. s. | 0 | . η.. . η′. | h. h′ | . ω.. . ϕ. | f. f ′ |
| . c.. c. | 0 | . η. c | hc | ψ | χc |
| . b.. b. | 0 | . η. b | hb | . ϒ. | χb |
| . t.. t. | 0 | . η. t | ht | . θ. | χt |
^C-четность актуальна только для нейтральных мезонов.. ^Для J = 1, ψ называется . J / ψ.
. Кроме того:
- Когда известно спектроскопическое состояние мезона, оно добавляется в скобки.
- Когда спектроскопическое состояние неизвестно, масса (в МэВ /c ) добавляется в скобках.
- Когда мезон находится в своем основном состоянии, в скобках ничего не добавляется.
Ароматизированные мезоны
Ароматизированные мезоны – это мезоны, состоящие из пары кварков и антикварков разного вкуса. В этом случае правила проще: главный символ зависит от более тяжелого кварка, верхний индекс зависит от заряда, а нижний индекс (если есть) зависит от более легкого кварка. В табличной форме это:
| Кварк | Антикварк | |||||
|---|---|---|---|---|---|---|
| up | вниз | шарм | странный | наверх | снизу | |
| up | — | . D. | . K. | . T. | . B. | |
| вниз | — | . D. | . K. | . T. | . B. | |
| очарование | . D. | . D. | — | . D. s | . T. c | . B. c |
| странно | . K. | . K. | . D. s | — | . T. s | . B. s |
| сверху | . T. | . T. | . T. c | . T. s | — | . T. b |
| снизу | . B. | . B. | . B. c | . B. s | . T. b | — |
Дополнительно:
- Если J входит в “нормальную серию” “(т. е. J = 0, 1, 2, 3,…), добавляется верхний индекс ∗.
- Если мезон не псевдоскалярный (J = 0) или вектор (J = 1), J добавляется как нижний индекс.
- Когда известно спектроскопическое состояние мезона, оно добавляется в скобках.
- Когда спектроскопическое состояние неизвестно, в скобках добавляется масса (в МэВ /c ).
- Когда мезон находится в основном состоянии, в скобках ничего не добавляется.
Экзотические мезоны
Существуют экспериментальные доказательства того, что частицы являются адронами (т.е. состоят из кварков) и нейтральны по цвету с нулем барионное число, а значит, по общепринятому определению являются мезонами. Тем не менее, эти частицы не состоят из одной пары кварк / антикварк, как все другие обычные мезоны, рассмотренные выше. Предварительная категория для этих частиц: экзотические мезоны.
Существует по крайней мере пять экзотических мезонных резонансов, существование которых было экспериментально подтверждено двумя или более независимыми экспериментами. Наиболее статистически значимым из них является Z (4430), обнаруженный в эксперименте Belle в 2007 году и подтвержденный LHCb в 2014 году. тетракварк : частица, состоящая из двух кварков и двух антикварков. См. Основную статью выше, в которой описаны резонансы других частиц, которые могут быть экзотическими мезонами.
Список
Псевдоскалярные мезоны
| Имя частицы | Символ частицы. | Символ античастицы. | Содержание кварка. | Масса покоя (МэВ /c ) | I | J | S | C | B’ | Среднее время жизни (s ) | Обычно распадается до. (>5% распадов) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пион | . π. | . π. | . u. . d. | 139,57018 ± 0,00035 | 1 | 0 | 0 | 0 | 0 | (2,6033 ± 0,0005) × 10 | . μ. + . ν. μ |
| Пион | . π. | Я | uu ¯ – dd ¯ 2 { displaystyle mathrm { tfrac {u { bar {u}} – d { bar {d}}} { sqrt {2}}} ,} |
134.9766 ± 0.0006 | 1 | 0 | 0 | 0 | 0 | (8.4 ± 0.6) × 10 | . γ. + . γ. |
| Eta-мезон | . η. | Self | uu ¯ + dd ¯ – 2 сс ¯ 6 { displaystyle mathrm { tfrac {u { bar {u}} + d { bar {d}} – 2s { bar {s}}} { sqrt {6}}} ,} |
547,853 ± 0,024 | 0 | 0 | 0 | 0 | 0 | (5,0 ± 0,3) × 10 | . γ. + . γ. или. . π. + . π. + . π. или. . π. + . π. + . π. |
| простой мезон Этата | . η′. (958) | Self | uu ¯ + dd ¯ + ss ¯ 3 { displaystyle mathrm { tfrac {u { bar {u}} + d { bar {d}} + s { bar {s}}} { sqrt {3}} } ,} |
957,66 ± 0,24 | 0 | 0 | 0 | 0 | 0 | (3,2 ± 0,2) × 10 | . π. + . π. + . η. или. (. ρ. + . γ. ) / (. π. + . π. + . γ. ) или. . π. + . π. + . η. |
| Очарованный мезон эта | . η. c (1S) | Собственный | . c. . c. | 2980,3 ± 1,2 | 0 | 0 | 0 | 0 | 0 | (2,5 ± 0,3) × 10 | См.. η. cрежимы распада |
| Нижний эта-мезон | . η. b (1S) | Собственный | . b. . b. | 9300 ± 40 | 0 | 0 | 0 | 0 | 0 | Неизвестно | См.. η. bмоды распада |
| Каон | . K. | . K. | . u. . s. | 493,677 ± 0,016 | ⁄2 | 0 | 1 | 0 | 0 | (1,2380 ± 0,0021) × 10 | . μ. + . ν. μ or.
. π. + . π. или. . π. + . e. + . ν. e или. . π. + . π. |
| Kaon | . K. | . K. | . d. . s. | 497,614 ± 0,024 | ⁄2 | 0 | 1 | 0 | 0 | ||
| K-Short | . K. S | Self | ds ¯ – sd ¯ 2 { displaystyle mathrm { tfrac {d { bar {s}} – s { bar {d}}} { sqrt {2}}} ,} |
497,614 ± 0,024 | ⁄2 | 0 | (*) | 0 | 0 | (8,953 ± 0,005) × 10 | . π. + . π. или. . π. + . π. |
| K-Long | . K. L | Self | ds ¯ + sd ¯ 2 { displaystyle mathrm { tfrac {d { bar {s}} + s { bar { d}}} { sqrt {2}}} ,} |
497,614 ± 0,024 | ⁄2 | 0 | (*) | 0 | 0 | (5,116 ± 0,020) × 10 | . π. + . e. + . ν. e or. . π. + . μ. + . ν. μ или. . π. + . π. + . π. или. . π. + . π. + . π. |
| D-мезон | . D. | . D. | . c. . d. | 1869,62 ± 0,20 | ⁄2 | 0 | 0 | +1 | 0 | (1,040 ± 0,007) × 10 | См.. D. моды распада |
| D-мезон | . D. | . D. | . c. . u. | 1864,84 ± 0,17 | ⁄2 | 0 | 0 | +1 | 0 | ( 4,101 ± 0,015) × 10 | См.. D. моды распада |
| странный D-мезон | . D. s | . D. s | . c. . s. | 1968,49 ± 0,34 | 0 | 0 | +1 | +1 | 0 | (5,00 ± 0,07) × 10 | См.. D. sрежимы распада |
| B-мезон | . B. | . B. | . u. . b. | 5279,15 ± 0,31 | ⁄2 | 0 | 0 | 0 | +1 | (1,638 ± 0,011) × 10 | См.. B. режимы распада |
| B-мезон | . B. | . B. | . d. . b. | 5279,53 ± 33 | ⁄2 | 0 | 0 | 0 | +1 | (1,530 ± 0,009) × 10 | См.. B. режимы распада |
| Странный B мезон | . B. s | . B. s | . s. . b. | 5366,3 ± 0,6 | 0 | 0 | -1 | 0 | +1 | 1,470 + 0,026. -0,027 × 10 | См.. B. sмоды распада |
| Очарованный B-мезон | . B. c | . B. c | . c. . b. | 6276 ± 4 | 0 | 0 | 0 | +1 | +1 | (4,6 ± 0,7) × 10 | См.. B. cрежимы распада |
^Состав неточен из-за ненулевого кварка. ^PDG сообщает о резонансной ширине (Γ). Здесь вместо этого дается преобразование τ = ⁄ Γ.. ^Strong eigenstate. Нет определенного срока службы (см. примечания к каону ниже). ^Масса. K. Lи. K. Sдана как масса. K.. Однако известно, что существует разница между массами. K. Lи. K. Sпорядка 2,2 × 10 МэВ / c.. ^Слабое собственное состояние. В макияже отсутствует небольшой член, нарушающий CP (см. примечания к нейтральным каонам ниже).
Векторные мезоны
| Имя частицы. | Символ частицы. | Символ античастицы. | Кварк. содержание | Масса покоя (МэВ /c ) | I | J | S | C | B’ | Среднее время жизни (s ) | Обычно распадается до. (>5% распадов) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Заряженный ро-мезон | . ρ. (770) | . ρ. (770) | . u. . d. | 775,4 ± 0,4 | 1 | 1 | 0 | 0 | 0 | ~ 4,5 × 10 | . π. + . π. |
| нейтральный ро-мезон | . ρ. (770) | Сам | uu ¯ – dd ¯ 2 { displaystyle mathrm { tfrac {u { bar {u}} – d { bar {d}}} { sqrt {2}}}} |
775,49 ± 0,34 | 1 | 1 | 0 | 0 | 0 | ~ 4,5 × 10 | . π. + . π. |
| Омега мезон | . ω. (782) | Я | uu ¯ + dd ¯ 2 { displaystyle mathrm { tfrac {u { bar {u}} + d { bar {d}}} { sqrt {2}}}} |
782,65 ± 0,12 | 0 | 1 | 0 | 0 | 0 | (7,75 ± 0,07) × 10 | . π. + . π. + . π. или. . π. + . γ. |
| Phi-мезон | . ϕ. (1020) | Самостоятельное | . s. . s. | 1019,445 ± 0,020 | 0 | 1 | 0 | 0 | 0 | (1,55 ± 0,01) × 10 | . K. + . K. или. . K. S + . K. L или. (. ρ. + . π. ) / (. π. + . π. + . π. ) |
| Дж / Пси | . Дж / ψ. | Самостоятельное | . c. . c. | 3096,916 ± 0,011 | 0 | 1 | 0 | 0 | 0 | (7,1 ± 0,2) × 10 | См.. J / ψ. (1S) режимы распада |
| ипсилонный мезон | . ϒ. (1S) | Self | . b. . b. | 9460,30 ± 0,26 | 0 | 1 | 0 | 0 | 0 | (1,22 ± 0,03) × 10 | См. Режимы распада. ϒ. (1S) |
| Kaon | . K. | . K. | . u. . s. | 89 1,66 ± 0,026 | ⁄2 | 1 | 1 | 0 | 0 | ~ 7,35 × 10 | См.. K. (892) Режимы распада |
| Kaon | . K. | . K. | . d. . s. | 896,00 ± 0,025 | ⁄2 | 1 | 1 | 0 | 0 | (7,346 ± 0,002) × 10 | См.. K. ( 892) моды распада |
| D-мезон | . D. (2010) | . D. (2010) | . c. . d. | 2010,27 ± 0,17 | ⁄2 | 1 | 0 | +1 | 0 | (6,9 ± 1,9) × 10 | . D. + . π. или. . D. + . π. |
| D мезон | . D. (2007) | . D. (2007) | . c. . u. | 2006,97 ± 0,19 | ⁄2 | 1 | 0 | +1 | 0 | >3,1 × 10 | . D. + . π. или. . D. + . γ. |
| странный D-мезон | . D. s | . D. s | . c. . s. | 2112,3 ± 0,5 | 0 | 1 | +1 | +1 | 0 | >3,4 × 10 | . D. + . γ. или. . D. + . π. |
| B-мезон | . B. | . B. | . u. . b. | 5325,1 ± 0,5 | ⁄2 | 1 | 0 | 0 | +1 | Неизвестно | . B. + . γ. |
| B-мезон | . B. | . B. | . d. . b. | 5325,1 ± 0,5 | ⁄2 | 1 | 0 | 0 | +1 | Неизвестно | . B. + . γ. |
| Странный мезон B | . B. s | . B. s | . s. . b. | 5412,8 ± 1,3 | 0 | 1 | −1 | 0 | +1 | Неизвестно | . B. s +. γ. |
| Зачарованный B-мезон | . B. c | . B. c | . c. . b. | Неизвестно | 0 | 1 | 0 | +1 | +1 | Неизвестно | Неизвестно |
^PDG сообщает о ширине резонанса (Γ). Здесь вместо этого приводится преобразование τ = ⁄ Γ.. ^Точное значение зависит от используемого метода. См. Данную ссылку для подробностей.
Примечания к нейтральным каонам
Есть две сложности с нейтральными каонами :
- . Из-за смешивания нейтральных каонов, . K. S и . K. L не являются собственными состояниями странности. Однако они являются собственными состояниями слабой силы, которая определяет, как они распадаются, поэтому это частицы с определенным временем жизни .
- линейные комбинации, приведенные в таблице для . K. S и . K. L, не совсем верны, так как есть небольшая поправка из-за нарушения CP. См. нарушение CP в каонах..
Обратите внимание, что эти проблемы также существуют в принципе для других нейтральных ароматизированных мезонов; однако слабые собственные состояния считаются отдельными частицами только для каонов из-за их резко различающихся времен жизни.
См. также
- Стандартная модель
- Мезонная молекула
Примечания
Ссылки
Внешние ссылки
- Таблица некоторых мезонов и их свойств
- Группа данных о частицах – собирает достоверную информацию о свойствах частиц
- hep-ph / 0211411: легкие скалярные мезоны в кварковых моделях
- Схема присвоения имен адронам (файл PDF)
- Мезоны стали осмысленными, интерактивная визуализация, позволяющая сравнивать физические свойства
Недавние открытия
- Что случилось с антиматерией? Эксперимент Фермилаба DZero находит ключи в быстроменяющемся мезоне
- Эксперимент CDF окончательно обнаружил колебания материи-антивещества в Bs-мезоне





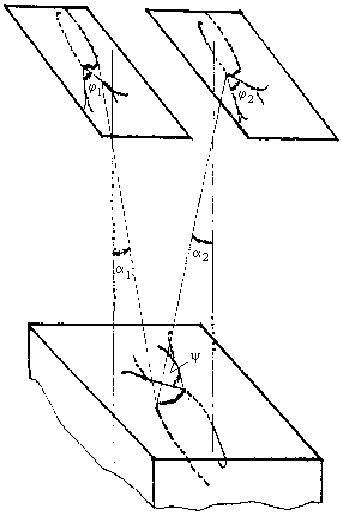

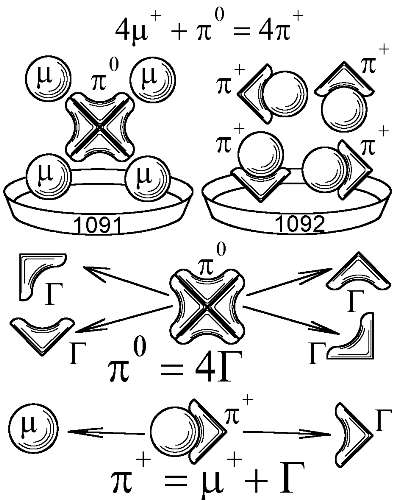
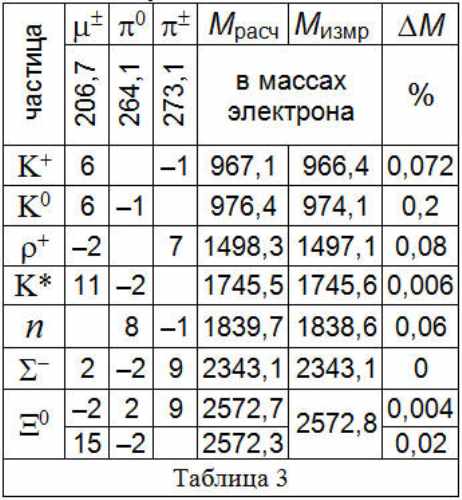






![{displaystyle I_{3}={frac {1}{2}}left[left(n_{text{u}}-n_{bar {text{u}}}right)-left(n_{text{d}}-n_{bar {text{d}}}right)right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae39e46af2c05311fffc26b62677ba1b9542c356)


![{displaystyle Q={frac {2}{3}}[(n_{text{u}}-n_{bar {text{u}}})+(n_{text{c}}-n_{bar {text{c}}})+(n_{text{t}}-n_{bar {text{t}}})]-{frac {1}{3}}[(n_{text{d}}-n_{bar {text{d}}})+(n_{text{s}}-n_{bar {text{s}}})+(n_{text{b}}-n_{bar {text{b}}})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc09b0b6a2676dcfb882e674c8b135ce1456da09)


![I_ {3} = { frac {1} {2}} [(n_ {u} -n _ { bar {u}}) - (n_ {d} -n _ { bar {d}})],](https://wikimedia.org/api/rest_v1/media/math/render/svg/304b8b17962d8aa23e7dbdb82a8b5e114d59a922)




![Q = { frac {2} {3}} [(n_ {u} -n _ { bar {u}}) + (n_ {c} -n _ { bar {c}}) + (n_ {t} -n_ { bar {t}})] - { frac {1} {3}} [(n_ {d} -n _ { bar {d}}) + (n_ {s} -n _ { bar {s} }) + (n_ {b} -n _ { bar {b}})].](https://wikimedia.org/api/rest_v1/media/math/render/svg/2819b98f91f3a602eb120eb3e8d5575661f1150e)
