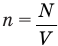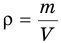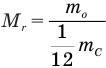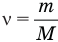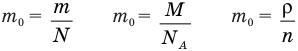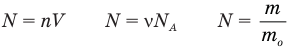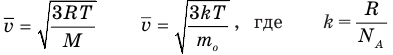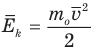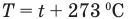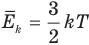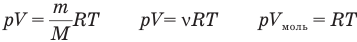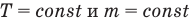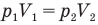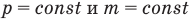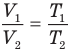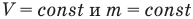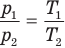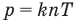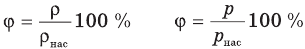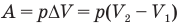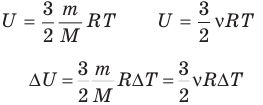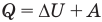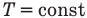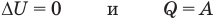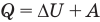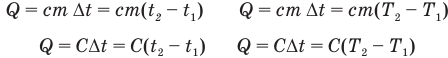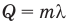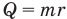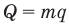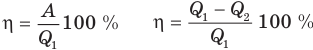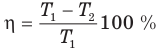Как найти массу одной молекулы вещества
Молекула вещества является одновременно минимально возможной его порцией, а потому именно ее свойства являются определяющими для вещества в целом. Эта частица принадлежит микромиру, поэтому рассмотреть, а тем более взвесить ее, не представляется возможным. Но массу одной молекулы можно рассчитать.
Вам понадобится
- – периодическая таблица химических элементов;
- – понятие о строении молекулы и атома;
- – калькулятор.
Инструкция
Если известна химическая формула вещества, определите его молярную массу. Для этого определите атомы, из которых состоит молекула, и найдите их относительные атомные массы в периодической системе химических элементов. Если один атом встречается в молекуле n раз, умножьте его массу на это число. Затем сложите найденные значения и получите молекулярную массу данного вещества, которая равна его молярной массе в г/моль. Найдите массу одной молекулы, поделив молярную массу вещества M на постоянную Авогадро NА=6,022∙10^23 1/моль, m0=M/ NА.
Пример Найдите массу одной молекулы воды. Молекула воды (Н2О) состоит из двух атомов водорода и одного атома кислорода. Относительная атомная масса водорода равна 1, для двух атомов получим число 2, а относительная атомная масса кислорода равна 16. Тогда молярная масса воды будет равна 2+16=18 г/моль. Определите массу одной молекулы: m0=18/(6,022^23)≈3∙10^(-23) г.
Массу молекулы можно рассчитать, если известно количество молекул в данном веществе. Для этого поделите общую массу вещества m на количество частиц N (m0=m/N). Например, если известно, что в 240 г вещества содержится 6∙10^24 молекул, то масса одной молекулы составит m0=240/(6∙10^24)=4∙10^(-23) г.
Определите массу одной молекулы вещества с достаточной точностью, узнав количество протонов и нейтронов, которые входят в состав ее ядер атомов, из которых она состоит. Массой электронной оболочки и дефектом масс в данном случае следует пренебречь. Массу протона и нейтрона берите равной 1,67∙10^(-24) г. Например, если известно, если молекула состоит из двух атомов кислорода, какова ее масса? Ядро атома кислорода имеет в своем составе 8 протонов и 8 нейтронов. Общее количество нуклонов 8+8=16. Тогда масса атома равна 16∙1,67∙10^(-24)=2,672∙10^(-23) г. Поскольку молекула состоит из двух атомов, то ее масса равна 2∙2,672∙10^(-23)=5,344∙10^(-23) г.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Каждому человеку известно, что окружающие нас тела состоят из атомов и молекул. Они имеют разную форму и структуру. При решении задач по химии и физике часто требуется найти массу молекулы. Рассмотрим в данной статье несколько теоретических методов решения данной задачи.
Общие сведения
Прежде чем рассматривать, как найти массу молекулы, следует познакомиться с самим понятием. Далее приведем несколько примеров.
Молекулой принято называть совокупность атомов, которые объединены друг с другом тем или иным видом химической связи. Также они должны и могут рассматриваться, как единое целое в различных физико-химических процессах. Эти связи могут носить ионный, ковалентный, металлический или вандерваальсовский характер.
Всем известная молекула воды имеет химическую формулу H2O. Атом кислорода в ней соединен с помощью полярных ковалентных связей с двумя атомами водорода. Такое строение обуславливает многие физические и химические свойства жидкой воды, льда и пара.
Природный газ метан – это еще один яркий представитель молекулярного вещества. Его частицы образованы атомом углерода и четырьмя атомами водорода (CH4). В пространстве молекулы имеют форму тетраэдра с углеродом в центре.
Воздух – сложная смесь газов, которая главным образом состоит из молекул кислорода O2 и азота N2. Оба типа соединены прочными двойными и тройными ковалентными неполярными связями, что обуславливает их высокую химическую инертность.
Определение массы молекулы через ее молярную массу
В периодической таблице химических элементов содержится большое количество информации, среди которой имеются атомные единицы массы (а.е.м.). Например, атом водорода имеет а.е.м., равную 1, а атом кислорода – 16. Каждая из этих цифр показывает массу в граммах, которую будет иметь система, содержащая 1 моль атомов соответствующего элемента. Напомним, что единица измерения количества вещества 1 моль представляет собой количество частиц в системе, соответствующее числу Авогадро NA, оно равно 6,02*1023.
Когда рассматривают молекулу, то пользуются понятием не а.е.м., а молекулярной массой. Последняя представляет собой простую сумму а.е.м. для атомов, входящих в состав молекулы. Например, молярная масса для H2O будет равна 18 г/моль, а для O2 – 32 г/моль. Имея общее понятие, далее можно перейти к расчетам.
Молярную массу M просто использовать для вычисления массы молекулы m1. Для этого следует воспользоваться простой формулой:
m1 = M/NA.
В некоторых задачах может быть дана масса системы m и количество вещества в ней n. В таком случае масса одной молекулы вычисляется так:
m1 = m/(n*NA).
Идеальный газ
Этим понятием называется такой газ, молекулы которого хаотично движутся в разных направлениях с большими скоростями, друг с другом не взаимодействуют. Расстояния между ними намного превышают их собственные размеры. Для такой модели оказывается справедливым следующее выражение:
P*V = n*R*T.
Оно носит название закона Менделеева-Клапейрона. Как видно, уравнение связывает между собой давление P, объем V, абсолютную температуру T и количество вещества n. В формуле R – газовая константа, численно равная 8,314. Записанный закон называется универсальным, потому что он не зависит от химического состава системы.
Если известны три термодинамических параметра – T, P, V и значение m системы, то масса молекулы идеального газа m1 не сложно определить по следующей формуле:
m1 = m*R*T/(NA*P*V).
Это выражение также можно записать через плотность ρ газа и постоянную Больцмана kB:
m1 = ρ*kB*T/P.
Пример задачи
Известно, что плотность некоторого газа составляет 1,225 кг/м3 при атмосферном давлении 101325 Па и температуре 15 oC. Чему равна масса молекулы? О каком газе идет речь?
Поскольку нам даны давление, плотность и температура системы, то можно воспользоваться полученной в предыдущем пункте формулой, чтобы определить массу одной молекулы. Имеем:
m1 = ρ*kB*T/P;
m1 = 1,225*1,38*10-23*288,15/101325 = 4,807*10-26 кг.
Чтобы ответить на второй вопрос задачи, найдем молярную массу M газа:
M = m1*NA;
M = 4,807*10-26*6,02*1023 = 0,029 кг/моль.
Полученное значение молярной массы соответствует газу воздуху.
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 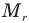

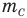
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 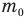
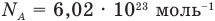



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

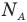
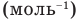

Формулы средней квадратичной скорости молекул
Здесь 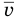
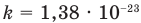

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

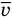

Формула средней кинетической энергии молекул
Здесь 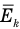
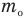
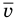
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
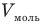
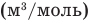
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 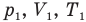

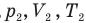

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 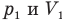

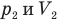

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 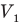
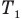

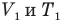

Закон Шарля
при
Здесь V — объем газа 
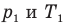
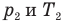
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 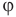
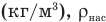
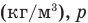
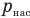
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 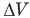
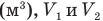

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 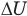
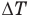
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
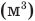
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 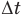
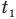
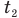
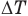
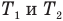
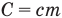
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 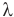
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
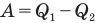
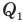
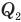
Коэффициент полезного действия идеального теплового двигателя
Здесь 
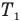
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Масса молекул.
В силу
исторических причин массы атомов и
молекул измеряются в относительных
единицах массы. Относительные массы
называют ещё атомными единицами массы
(а.е.м.). За единицу атомной массы
принимается 1/12 массы атома углерода
6С12,
т.е. 1(а.е.)=1/12m(6С12)=1,66·10-27
кг.
Например масса атома кислорода m(О)=16
(а.е.),
а масса атома углерода m(С)=12
(а.е.м.).
Массу
молекулы, выраженную в атомных единицах,
будем называть молекулярной
массой.
Относительная
масса
равна отношению массы одной молекулы
к 1/12
массы атома углерода 6С12
. (1.1)
Относительная
масса
– это число и она не имеет единиц
измерения, но численно равна молекулярной
массе. Чтобы найти относительную массу
молекулы используют свойство аддитивности
массы. Мы будем просто складывать массы
атомов в (а.е.м.)
из которых состоит данная молекула.
Массы атомов возьмём из таблицы
Менделеева. Найдём относительную массу
молекулы воды
. (1.2)
Физические
тела состоят из очень большого числа
молекул или атомов, поэтому для определения
количества вещества используют
определённые порции, в которых содержится
одно и тоже число молекул или атомов.
Это число называют числом
Авогадро.
Обозначим его как NА,
тогда в 2-х порциях вещества содержится
2NА
молекул, в 3-х – 3NА,
в
порциях – ·NА
молекул. Из наших рассуждений следует,
что для нахождения числа молекул N
в веществе нужно количество порций
умножить на число Авогадро
N=·NА.
Число ν равное
, (1.3)
называют количеством
вещества. Количество
вещества – это число, которое показывает
во сколько раз число молекул в данном
веществе, превосходит число Авогадро.
В Международной системе единиц СИ
количество вещества
выражают в молях. По определению один
моль – это
количество вещества, в котором содержится
столько же атомов или молекул, сколько
их содержится в 0,012 кг углерода 6С12.
Значит, в одном моле любого вещества
содержится одно и тоже число атомов или
молекул, равное числу Авогадро. Найдём
это число, учитывая, что масса атома
углерода равна m(6С12)=12
а.е. Для
этого массу всех атомов, содержащихся
в одном моле углерода, 0,012
кг разделим
на массу одного атома
(моль-1). (1.4)
Массу вещества,
взятого в количестве одного моля, будем
называть молярной
массой, и
обозначать буквой .
Молярная масса по определению равна
(кг/моль). (1.5)
С другой стороны
молярную массу можно найти, разделив
массу всего вещества М
на число его молей (порций)
. (1.6)
Масса любого
вещества может быть найдена как
произведение массы одной молекулы mмол
на число всех молекул M
= mмол·N.
Учитывая, что
(1.7)
получим
. (1.8)
По формуле (1.7) мы
может определить массу молекулы любого
вещества. Например, определим массы
молекул воды. Относительные массы
кислорода и воды найдём из таблицы
Менделеева. Молярная масса равна
относительной умноженной на 10-3,
поэтому для для воды (Н2О)=2+16=18·10-3
(кг/моль).
Вычислим массу молекулы
(кг). (1.9)
Лекция № 2. Идеальный газ. Основное уравнение мкт.
В зависимости от
характера взаимодействия молекул
вещество может находиться в трёх
агрегатных состояниях. Рассмотрим
газообразное состояние вещества. Пусть
некоторый газ находится в закрытом
сосуде. Молекулы газа непрерывно и
хаотично движутся, постоянно сталкиваются
друг с другом и со стенками сосуда.
Ударяясь о стенки сосуда, газ оказывает
на них давление, т.е. действует с некоторой
силой на единицу площади
. (2.1)
В нашем случае
давление газа – это результат действия
очень большого числа молекул на единичную
поверхность. Каждую секунду о поверхность
ударяется разное число молекул, поэтому
сила F,
а значит и давление Р
различно для различных моментов времени.
В формуле (2.1) давление газа является
средней величиной, которая характеризует
действие всех молекул на протяжении
некоторого интервала времени. Усреднёнными
значениями могут быть описаны и другие
величины, например температура. Метод
описания свойств макроскопических
систем на основе усреднённых значений
называется молекулярно-кинетическим
методом.
Давление газа
может измеряться:
-
В Международной
системе единиц в паскалях
– это сила величиной в 1 Н, действующая
на единичную поверхность [P]=Н/м2=Па. -
В миллиметрах
ртутного столба (мм.рт.ст.)
– это давление, производимое 1 миллиметром
ртутного столба на горизонтальную
поверхность, т.е.
Р=ρgh. Табличное
значение для плотности ртути
= 13,6·103
кг/м3,
g
= 9,81
м/с2
– ускорение свободного падения, поэтому
(2.2)
-
Физической
атмосферой (атм)
– это давление производимое столбом
ртути высотой в 760
мм.рт.ст.
на горизонтальную поверхность.
(2.3)
Эта величина
принимается за нормальное
атмосферное давление. Если давление
газа является нормальным и его температура
0°С, то говорят, что газ находится при
нормальных
условиях.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи по химии
Анонимный вопрос
23 января 2018 · 225,1 K
ОтветитьУточнить
Анна2,5 K
Образование: высшее (бакалавр + магистр). Увлечения: спорт, путешествие, кофе:) · 29 янв 2018
Решение: Массу одной молекулы кислорода можно рассчитать по формуле: m = М/Na, где M – молярная масса кислорода (М = 0,032 кг/моль), Na – число Авогадро (Na = 6*10^23 моль^-1). Рассчитаем массу одной молекулы кислорода: m = М/Na = 0,032/6*10^23 = 5,33*10^-26 кг.
Ответ: Масса одной молекулы кислорода равна 5,33*10^-26 кг.
121,8 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос