Как найти массу одного предмета в физике

Тогда ускорение свободного падения (g) относительно Земли определяется действием сил: гравитационной силы относительно Земли () и инерционной силы (). Гравитация является результатом действия этих сил:

Формула массы тела

В ньютоновской механике масса тела — это скалярная физическая величина, которая является мерой его инерционных свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.

Масса является аддитивной величиной, т.е: Масса каждой группы материальных точек (m) равна сумме масс всех отдельных частей системы (m_i):

В классической механике предполагается, что:

• масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
• выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.

Инертная масса

Инерционное свойство материальной точки заключается в том, что при приложении к ней внешней силы точка имеет конечное по модулю ускорение. Когда внешняя сила не приложена, тело находится в состоянии покоя в инерциальной системе координат или движется равномерно и прямолинейно. Масса входит во второй закон движения Ньютона:

Масса определяет инерционные свойства материальной точки (инерционная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, тем самым определяя гравитационные свойства конкретной точки; она называется гравитационной (тяжелой) массой.

Эмпирически установлено, что отношение инерционной массы к гравитационной массе одинаково для всех тел. Если значение гравитационной постоянной выбрано правильно, то из этого следует, что для каждого тела инерционная и гравитационная массы равны и относятся к гравитационной силе (F_t) выбранного тела:

Где g — ускорение свободного падения. Если наблюдения проводятся в одной и той же точке, то ускорение, вызванное гравитацией, будет одинаковым.

Энергия

Выше были приведены различные формулы для определения массы в физике. В заключение статьи я хотел бы указать на взаимосвязь между массой и энергией. Эта связь является фундаментальной и отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула для массы в физике, выведенная Альбертом Эйнштейном, имеет вид:

Квадрат скорости света c является коэффициентом преобразования между массой и энергией. Это выражение показывает, что обе величины по сути являются одним и тем же свойством материи.

Написанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.

Формулы для инерции

В физике формула для определения инерционной массы имеет следующий вид:

Здесь F — сила, действующая на тело и придающая ему ускорение a. Формула показывает, что чем больше действующая сила и чем меньше ускорение, которое она придает телу, тем больше инерционная масса m.

Помимо письменного выражения, для определения массы в физике необходимо привести еще одну формулу, которая связана с инерционным эффектом. Эта формула имеет вид:

Где p — масса движения (импульс), v — скорость тела. Чем больше движение тела и чем меньше его скорость, тем больше инерционная масса тела.

Примеры решения задач

Задача 1

Имеется алюминиевый стержень со сторонами 3, 5 и 7 см. Какова его масса?

Читайте также.

Определим объем стержня:

V = 3 * 5 * 7 = 105 см3 ,

Значение таблицы плотности алюминия: 2800 кг/м 3 или 2,8 г/см 3 ,

Вычислим массу стержня:

m = 105 * 2,8 = 294 г.

Задача 2

Проблема по смежной теме.

Сколько энергии необходимо для доведения воды комнатной температуры (20 градусов Цельсия) из стакана (емкостью 200 мл) до температуры кипения?

Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений были обобщены в 17 веке Исааком Ньютоном в законе всемирного тяготения. Согласно этому закону, два тела с массами m1 и m2 перемещаются под действием силы F

F = G * m1 * m2 / r2

Где r — расстояние между телами, G — константа.

Если мы подставим в это выражение массу нашей планеты и ее радиус, то получим следующую формулу массы в физике:

Где F — сила тяжести, а g — ускорение, с которым тело падает на землю вблизи ее поверхности.

Хорошо известно, что наличие гравитации гарантирует, что все тела имеют вес. Многие люди путают вес и массу и считают, что это одно и то же. Хотя эти две величины связаны между собой коэффициентом g, масса является переменной величиной (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса — в килограммах.

Читайте также: Металлоискатель ручной работы — 96 фото конструкции чувствительного прибора.

Весы, которыми человек пользуется дома (механические, электронные), показывают вес тела, но они измеряют вес тела. Пересчет между этими величинами — это просто вопрос калибровки прибора.

Формула зависимости массы от объема и плотности

Для определения плотности жидкости или твердого тела существует основная формула: Плотность равна массе, деленной на объем. Она записывается следующим образом: p = m / V

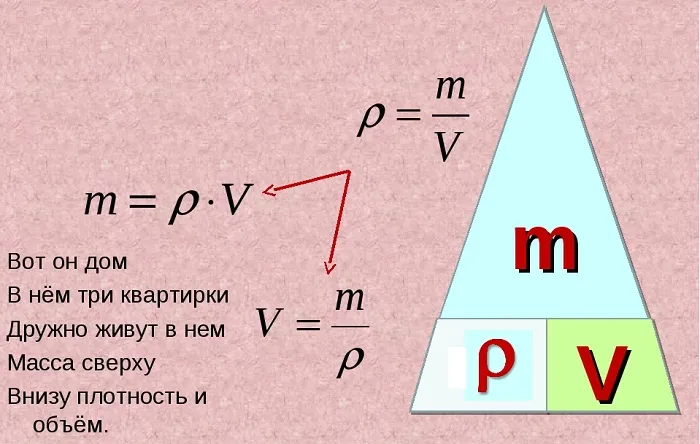
Отсюда можно вывести еще две формулы. Формула для объема тела: V = m / p А также формула для расчета массы: m = V * p Как видите, запомнить последнюю очень легко: это единственная формула, где нужно перемножить две единицы. Для запоминания этой зависимости можно использовать фигуру в виде «пирамиды», разделенной на три части, с массой в верхней части и плотностью и объемом в нижних углах. Ситуация с газами несколько иная. Вычислить их вес гораздо сложнее, поскольку газы не имеют постоянной плотности: Они рассеиваются и занимают весь доступный им объем. Именно здесь возникает понятие молекулярной массы, которую можно определить, сложив массы всех атомов в формуле вещества, используя данные из периодической таблицы.

Вторая необходимая нам единица — это количество вещества в молях. Это можно рассчитать с помощью уравнения реакции. Подробнее об этом вы можете узнать на уроке химии. Другой способ найти количество молей — разделить объем газа на 22,4 литра. Последнее число — это константа объема, которая называется s

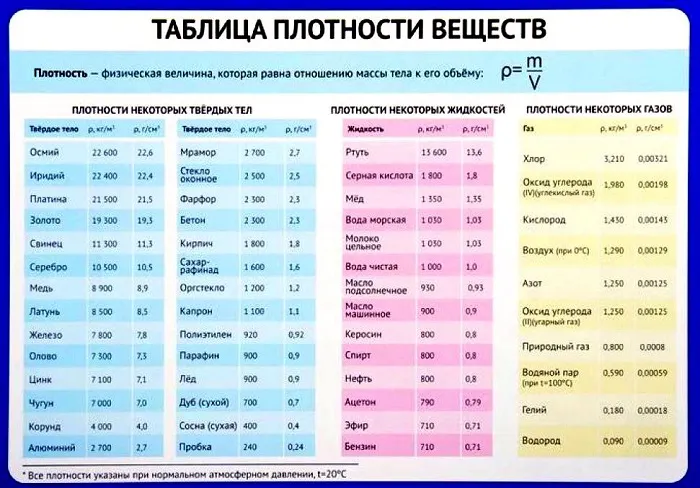
Плотность многих веществ известна заранее и может быть легко получена из соответствующей таблицы. При работе с устройством важно обращать внимание на размеры и помнить, что все данные собраны при нормальных условиях: Температура в помещении 20 градусов Цельсия, а также определенное давление, влажность и так далее.

Таблица плотности некоторых веществ

Плотности других, более редких веществ можно найти в Интернете. Стоит запомнить хотя бы одно значение плотности, так как оно часто встречается в задачах. Это плотность воды — 1000 кг/м3 или 1 г/см3.

Состояние: Имеется алюминиевый стержень с длиной стороны 3, 5 и 7 см. Какова его масса? Решение. Ответ: m = 294 г.

Примеры решения задач

Задача 1

Проблема по смежной теме. Ситуация: Сколько энергии требуется, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (емкостью 200 мл) до температуры кипения? Решение: Найдем недостающую информацию: температура кипения воды t

Задача 2

= 100 градусов Цельсия, удельная теплоемкость воды c = 4200 Дж/кг*C, плотность воды 1 г/см 3, 1 мл воды = 1 см 3. Найти массу воды: m = V * p, m = 200 * 1 = 200 г = 0,2 кг, найти энергию: Q = c * m * (t₂Q = 4200 * 0,2 * (100 — 20) = 67200 Дж = 67,2 кДж. Ответ: Q = 67,2 кДж.₂– t₁Проблема молекулярной массы. Условие: Определите массу CO

Задача 3

объемом 5,6 л. Решение: Определите молярную массу CO₂M = 12 + 16 * 2 = 44 г/моль; определите объем вещества: n = 5,6 / 22,4 = 0,25 моль; определите массу: m = n * M; m = 0,25 * 44 = 11 г. Ответ: m = 11 г.₂

Многие из нас в школьное время задавались вопросом: «Как найти массу тела»? Сейчас мы попытаемся ответить на этот вопрос.

Нахождение массы через его объем

Допустим, в вашем распоряжении есть бочка на двести литров. Вы намерены целиком заполнить ее дизельным топливом, используемом вами для отопления своей небольшой котельной. Как найти массу этой бочки, наполненной соляркой? Давайте попробуем решить эту простейшую на первый взгляд задачу вместе с вами.

Решить задачу, как найти массу вещества через его объем, довольно легко. Для этого следует применить формулу удельной плотности вещества

p = m/v,

где p является удельной плотностью вещества;

m – его массой;

v – занимаемым объемом.

В качестве меры массы будут использоваться граммы, килограммы и тонны. Меры объёмов: сантиметры кубические, дециметры и метры. Удельная плотность будет вычисляться в кг/дм³, кг/м³, г/см³, т/м³.

Таким образом, в соответствии с условиями задачи в нашем распоряжении есть бочка объемом двести литров. Это значит, что ее объем равняется 2 м³.

Но вы хотите узнать, как найти массу. Из вышеназванной формулы она выводится так:

m = p*v

Сначала нам требуется найти значение р – удельной плотности дизельного топлива. Найти данное значение можно, используя справочник.

В книге мы находим, что р = 860,0 кг/м³.

Затем полученные значения мы подставляем в формулу:

m = 860*2 = 1720,0 (кг)

Таким образом, ответ на вопрос, как найти массу, был найден. Одна тонна и семьсот двадцать килограммов – это вес двухсот литров летнего дизтоплива. Затем вы можете точно так же сделать приблизительный расчет общего веса бочки и мощности стеллажа под бочку с соляром.

Нахождение массы через плотность и объем

Очень часто в практических заданиях по физике можно встретить такие величины, как масса, плотность и объем. Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.

Предметы, которые вам будут нужны:

1) Рулетка.

2) Калькулятор (компьютер).

3) Емкость для измерения.

4) Линейка.

Известно, что у предметов с равным объемом, но изготовленных из различных материалов, будет разная масса (например, металл и дерево). Массы тел, которые изготовлены из определенного материала (без пустот), прямо пропорциональны объему рассматриваемых предметов. В противном случае, константа – это отношение массы к объему предметы. Этот показатель называется «плотностью вещества». Мы будем его обозначать буквой d.

Теперь требуется решить задачу, как найти массу в соответствии с формулой d = m/V, где

m является массой предмета (в килограммах),

V является его объемом (в метрах кубических).

Таким образом, плотность вещества является массой единицы его объема.

Если вам необходимо найти плотность материала, из которого создан предмет, то следует воспользоваться таблицей плотностей, которую можно найти в стандартном учебнике по физике.

Объем предмета вычисляется по формуле V = h * S, где

V – объем (м³),

H – высота предмета (м),

S – площадь основания предмета (м²).

В том случае, если вы не можете четко измерить геометрические параметры тела, то вам следует прибегнуть к помощи законов Архимеда. Для этого вам понадобится сосуд, у которого есть шкала, служащая для измерений объема жидкостей и опустить предмет в воду, то есть в сосуд, на котором есть деления. Тот объем, на который будет увеличено содержимое сосуда, является объемом тела, которое погружено в него.

Зная объем V и плотность d предмета, вы можете легко найти его массу по формуле m = d * V. Перед тем, как вычислить массу, требуется привести все измерительные единицы в единую систему, например, в систему СИ, являющуюся интернациональной измерительной системой.

В соответствии с вышеназванными формулами можно сделать следующий вывод: для нахождения требуемой величины массы с известным объемом и известной плотностью требуется умножить значение плотности материала, из которого изготовлено тело, на объем тела.

Содержание:

1. Масса
2. Второй закон Ньютона
3. Масса — мера инертности тела
4. Система единиц измерения механических величин
5. Примеры решения задач на второй закон Ньютона

Масса – это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Масса

Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.

Массой тела называется количество вещества, содержащегося в этом теле.

Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.

Рис. 98. Измерение массы тела.

Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.

За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.

В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).

В практике эталоны масс изготовляют в виде гирь различной величины.

Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.

Второй закон Ньютона

Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.

Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.

Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле  определяем ускорение а.

Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.

Результаты таких измерений и вычислений отражены в таблице.

Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.

Математически это можно записать в виде формулы:

Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.

Нагружая тележку гирями, изменим массу движущихся тел.

Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.

Результаты опытов снова занесём в таблицу.

Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:

Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.

Кроме того, ускорение тела совпадает с этой силой по направлению.

Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.

Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.

Второй закон Ньютона математически можно выразить в виде следующей формулы:

откуда

Величина силы равна произведению массы тела на ускорение.

Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.

В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:

Р = mg.

Из сопоставления формулы F=ma и P=mg видно, что

т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.

При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.

Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением  Определить силу, движущую санки.

Р=70 кГ;

g=
а =
F = ?

Из формулы определим F: 

Масса — мера инертности тела

Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.

Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.

Рис. 100. Масса наковальни значительно больше массы молота.

Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.

Итак, масса тела является мерой его инертности. 

Из второго закона Ньютона  следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.

Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.

Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.

Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.

Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.

Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.

Рис. 101. Машина на массивном фундаменте.

Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.

Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:

Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.

Система единиц измерения механических величин

Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.

Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в

Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.

Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.

В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).

Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).

Единица скорости в этой системе единица ускорения 

Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:

За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным Эта единица называется диной (сокращённо дн).

В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:

единица длины  — 1  м,

единица массы  — 1  кг,

единица времени  — 1 сек,

единица тока  — 1  ампер.

Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).

Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением  Эта единица называется ньютон (сокращённо н). Таким образом,

Вычислим, сколько в одном ньютоне содержится дин. или  
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:

единица длины —1 м,

единица силы —1 кГ,

единица времени—1 сек.

Единица массы в этой системе единиц является производной и может быть определена из равенства т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением

Сокращённое обозначение этой единицы—т. е. м. Таким образом,

Между различными единицами массы и силы существуют следующие соотношения:

1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение Отсюда:  или округлённо:

Так как то 1 кГ = 9,8 н.

Примеры решения задач на второй закон Ньютона

1.    Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?

Расчёты ведём в системе CGS.

Дано: F = 2 кГ=2*980000 дн = 1960000 дн;

m=19600 г; t = 5 сек. Найти 

Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:

Время t дано по условиям задачи.

Ускорение найдем на основании второго закона:

Ответ: 
2.    Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.

Дано: Р = 98 кГ;  t = 300 сек. Найти F.

Искомую силу найдём на основании второго закона:

F = mа.

Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;

Так как то

 и

По второму закону Ньютона Р = mg, откуда
 

Ответ. 

3. На тело, движущееся с начальной скоростью в  подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.

Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона: 

Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, ускорение а по условиям задачи вычислим по формуле:

откуда

Масса тела 

Ответ.

При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.

Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.

Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.

Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.

m = 10 г; t = 60 сек.; s = 1800 см.

По второму закону Ньютона F = ma.    (1)

Масса дана, ускорение а находим по формуле пути равноускоренного движения: откуда

Подставим значение а из равенства (2) в равенство (1), получим:

Подставляя численные значения величин в равенство (3), определим величину силы F:

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Взаимодействия тел
7. Механическая энергия
8. Импульс
9. Вращение твердого тела
10. Криволинейное движение тел
11. Колебания
12. Колебания и волны
13. Механические колебания и волны
14. Бегущая волна
15. Стоячие волны
16. Акустика
17. Звук
18. Звук и ультразвук
19. Движение жидкости и газа
20. Молекулярно-кинетическая теория
21. Молекулярно-кинетическая теория строения вещества
22. Молекулярно – кинетическая теория газообразного состояния вещества
23. Теплота и работа
24. Температура и теплота
25. Термодинамические процессы
26. Идеальный газ
27. Уравнение состояния идеального газа
28. Изменение внутренней энергии
29. Переход вещества из жидкого состояния в газообразное и обратно
30. Кипение, свойства паров, критическое состояние вещества
31. Водяной пар в атмосфере
32. Плавление и кристаллизация
33. Тепловое расширение тел
34. Энтропия
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома