Как найти массу планеты астрономия

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

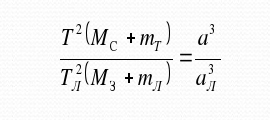
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Как найти массу планеты формула астрономия

Астрономия — это наука о небесных телах, и в ее основе лежит желание понять мир за пределами нашей Земли. Среди самых важных задач для астрономов — определение массы планеты. Почему это так важно? На это есть несколько причин.

Зачем находить массу планеты?

Определение массы планеты имеет несколько важных научных и практических применений.

• Представление об устройстве планетной системы. С точки зрения астрономии, планеты — это всего лишь маленькие тела, движущиеся вокруг звезды. Однако каждой планете придается большое значение, и сравнительное изучение их массы помогает увидеть, как они взаимодействуют друг с другом.
• Оценка возможности развития жизни. Исследования показывают, что существует определенный диапазон масс планет, при которых возможно существование жизни. Например, планеты слишком малых масс не могут удерживать атмосферу, а слишком большие могут иметь слишком высокие давления и температуры на поверхности.
• Исследование физических свойств планеты. Масса позволяет установить такие характеристики как плотность, гравитационное влияние, орбита, радиус и т.д.

Как найти массу планеты?

Масса планеты может быть измерена разными способами, но самой точной является методика, основанная на третьем законе Кеплера. Этот закон утверждает, что для любой планеты, вращающейся вокруг звезды, есть фиксированное отношение между ее периодом обращения вокруг звезды и расстоянием до звезды.

Конкретно, квадрат периода обращения планеты вокруг звезды равен кубу ее расстояния до звезды, умноженному на гравитационную постоянную.

Это означает, что если вы измерите период обращения планеты, то сможете определить ее расстояние до звезды. Затем, если вы найдете ее орбитальную скорость, вы сможете вычислить ее массу, используя закон всемирного тяготения.

Масса планеты равна произведению куба ее периода обращения вокруг своей оси и квадрата ее орбитальной скорости, деленному на гравитационную постоянную.

Эта формула, называемая «формулой Барнера», является фундаментальной в астрономии и используется для измерения массы не только планет, но и звезд, галактик и других тел.

Заключение

Измерение массы планеты может показаться сложной задачей, но с помощью таких принципов, как закон Гука и закон всемирного тяготения, астрономы могут точно определить ее физические характеристики. Как мы обсудили, это имеет несколько важных научных и практических применений, от установления возможности развития жизни до изучения устройства нашей солнечной системы и Вселенной в целом.

Как найти массу планеты формула астрономия

Астрономия – это наука, которая изучает небесные тела, включая нашу солнечную систему. Одним из ключевых параметров планет является их масса, которая определяет гравитационное влияние, орбиту и другие свойства.

Как измерить массу планеты?

Существует несколько методов измерения массы планеты, включая:

• Изучение орбиты спутника
• Анализ гравитационного воздействия
• Спектральный анализ
• Изучение эффекта Доплера

Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной планеты и ее свойств. Для измерения массы Земли, например, используют метод анализа гравитационного поля, тогда как для измерения массы Юпитера – метод изучения орбиты его лун.

Формула для расчета массы планеты

Самым распространенным методом измерения массы планеты является анализ ее гравитационного воздействия на другие небесные тела, например, на спутники или на другие планеты. Для рассчета массы планеты используется следующая формула:

масса планеты = масса Солнца * период2 / (4π2 * r3)

где:

• масса Солнца – масса Солнца в кг
• период – период обращения планеты вокруг Солнца в секундах в квадрате
• r – среднее расстояние планеты от Солнца в метрах в кубе

Эта формула основывается на законах Ньютона и применяется для расчета массы планеты на основе ее гравитационного воздействия на другие тела. Однако, этот метод не является идеальным, так как он основывается на предположении, что планета имеет симметричную форму, что не всегда соответствует действительности.

Пример расчета массы планеты

Давайте рассмотрим пример расчета массы Земли на основе ее гравитационного воздействия на Луну. Период обращения Луны вокруг Земли составляет 27,3 дня, а среднее расстояние Луны от Земли составляет 384 400 км.

Используя формулу:

масса Земли = масса Солнца * период2 / (4π2 * r3)

мы можем рассчитать массу Земли, зная массу Солнца (1,989 × 10^30 кг). Подставим известные значения в формулу:

масса Земли = (1,989 × 10^30 кг) * (27,3 * 86400 с)^2 / (4π2 * (384400 км * 1000 м / км))^3 ≈ 5,97 × 10^24 кг

Таким образом, мы получили, что масса Земли составляет приблизительно 5,97 × 10^24 кг.

Вывод

Масса планеты является ключевым параметром, который определяет множество свойств планеты, таких как ее гравитационное воздействие, орбита и т.д. Существует несколько методов измерения массы планеты, и самым распространенным из них является метод анализа ее гравитационного воздействия на другие небесные тела. Для расчета массы планеты используется формула, которая основывается на законах Ньютона и позволяет точно рассчитать массу планеты на основе ее гравитационного воздействия на другие тела.

Как найти массу планеты формула астрономии

Исследование космоса является одной из самых захватывающих и масштабных наук нашего времени. Одним из наиболее популярных объектов исследования являются планеты. Один из методов изучения планет — определение их массы. Как же найти массу планеты формулой астрономии?

Что такое масса планеты?

Масса планеты — это количество материи, содержащееся в планете. Это важный параметр, который позволяет ученым оценить размер планеты и понять, какой вклад эта планета вносит в систему, в которой она находится.

Масса планеты измеряется в килограммах. Существует много разных методов измерения массы планет, но одним из наиболее точных и универсальных является метод измерения радиальной скорости.

Как измерить массу планеты?: Формула

Для вычисления массы планеты используется формула, которая учитывает известные параметры системы, в которой планета находится. Формула для определения массы планеты:

M = (m * a * (1 — e²)) / G

Где:

• M — масса планеты
• m — масса звезды
• a — расстояние между звездой и планетой
• e — эксцентриситет орбиты планеты
• G — гравитационная постоянная

Из этой формулы видно, что чтобы вычислить массу планет, необходимо знать массу звезды, расстояние между звездой и планетой, эксцентриситет орбиты планеты и гравитационную постоянную. Рассмотрим эти параметры более подробно.

Как найти массу звезды?

Для того, чтобы найти массу планеты, нужно сначала определить массу звезды в системе, в которой находится планета. Это можно сделать с помощью разных методов. Один из таких методов — это измерение скорости, с которой звезда двигается вокруг общего центра масс системы. Как правило, центр масс системы находится ближе к более массивному объекту. Поэтому, если скорость движения звезды известна, то можно вычислить ее массу, исходя из подразумеваемой массы планет, которые влияют на движение звезды.

Как найти расстояние между планетой и звездой?

Чтобы вычислить массу планеты, необходимо знать расстояние между звездой и планетой. Это расстояние можно найти, используя параллакс: измерение изменения положения звезды относительно фона звезд на фоне сферической координатной системы. Это делается с помощью передвижения спутника, который изменяет угол между направлением на звезду и направлением на фоновые звезды.

Как найти эксцентриситет орбиты планеты?

Эксцентриситет орбиты планеты — это параметр, который описывает форму орбиты, на которой движется планета. Эксцентриситет орбиты можно найти, используя данные о радиальной скорости планеты. Это возможно благодаря тому, что радиальная скорость планеты изменяется в зависимости от того, находится ли планета на самой близкой точке к звезде (перихелии) или самой дальней точке (апогее).

Как использовать формулу для нахождения массы планеты?

После того, как измерены масса звезды, расстояние между звездой и планетой и эксцентриситет орбиты, можно использовать формулу для нахождения массы планеты. Гравитационная постоянная G уже известна, и ее значение равно 6,67 х 10^-11 Н * м^2/кг^2.

Пример использования формулы:

M = (2 * 10^30 * 1.5 х 10^10 * (1 — 0.4²)) / (6,67 х 10^-11)

В этом примере мы имеем следующие значения:

• Масса звезды — 2*10^30 кг
• Расстояние между звездой и планетой — 1.5 * 10^10 м
• Эксцентриситет орбиты — 0.4

Подставляя значения в формулу, получим:

M = 1,192 х 10^25 кг

Таким образом, мы вычислили массу данной планеты, используя формулу и знания об измеряемых параметрах.

Вывод

Найдя массу планеты, ученые могут лучше понять, как планета взаимодействует с другими объектами в системе, включая звезды, гравитирующие к ней спутники и другие планеты. Найдя массу звезды, эксцентриситет орбиты и расстояние между звездой и планетой, вы можете использовать формулу, чтобы найти массу планеты. В конечном итоге, этот процесс поможет ученым получить более глубокое понимание космической системы и дать нам лучший взгляд на нашу галактику и ее составляющие части.

Масса – это одно из самых важных свойств материи. Являясь мерой гравитационного взаимодействия, именно она во многом определяет облик нашей Вселенной – от звезд и планет до галактических скоплений. Однако, измерение этой величины в космических масштабах – совсем не простая задача. Так как же ученые узнают массы планет, звезд и других небесных тел?

Начнем с относительно простого – массы Земли. В качестве основы нам понадобится закон всемирного тяготения, сформулированный Исааком Ньютоном еще в 1666 году. Согласно ему, сила притяжения двух тел прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между объектами.

Из него легко можно вывести формулу для ускорения свободного падения. В свою очередь, находясь на Земле, эту величину можно измерить различными способами. Самый очевидный из них – сбросить с высокой башни тяжелый предмет и засечь время падения. Другой вариант – изготовить из нитки и грузика простейший маятник, после чего замерить период его колебаний. Если вам интересно попробовать провести этот несложный, но занимательный эксперимент самостоятельно – напишите об этом в комментариях, и мы обязательно посвятим ему одну из ближайших статей.

Радиус же нашей планеты также можно определить с довольно высокой точностью, не покидая ее – древние греки справлялись с этим еще три тысячи лет назад. Для этого потребуется две астролябии – так называется прибор для измерения высоты небесных тел на небосводе. Кроме того, необходим знакомый в другом городе, часы и любой способ связи. Нужно всего лишь одновременно измерить высоту солнца над горизонтом в полдень, после чего решить несложное уравнение.

Таким образом, зная радиус нашей планеты и ускорение свободного падения, можно рассчитать массу Земли. Разумеется, чем точнее будут измерены исходные данные, тем ближе к истине окажетсяконечный результат вычислений.

Прямым следствием из закона всемирного тяготения является третий закон Кеплера, связывающий орбиты и массы небесных тел. С его помощью можно узнать массу Луны, зная параметры ее орбиты и массу нашей планеты. Аналогично вычисляется масса Солнца, а от нее – всех остальных планет нашей системы.

С дальними же светилами все обстоит намного сложнее. Параметры двойных звезд относительно просто определяются по их взаимному движению, главное – правильно измерить расстояния. В случае же одиночных светил используются различные косвенные методы.

Например, на основе огромного количества наблюдений была сформулирована зависимость массы звезды от ее светимости. К сожалению, белые карлики и пульсары не подчиняются этой закономерности, и их параметры приходится определять иными методами.

Еще одним способом является спектральный анализ излучения звезды. Дело в том, что ее собственная гравитация искажает линии спектра подобно доплеровскому смещению. Массы экзопланет определяют по их влиянию на собственное движение материнского светила, а звездных скоплений – как сумму масс составляющих их объектов. Параметры же далеких галактик вычисляются либо по их вращению, либо по средней скорости собственного движения их компонентов.

Естественно, что чем дальше расположен объект от Земли, тем меньше точность, с которой можно вычислить его параметры. Например, масса нашей планеты определена с точностью 0,05%, Луны и Солнца – 0,1%, планет системы – до 0,7%. В то же время, погрешность измерения характеристик некоторых звезд может составлять от 20 до 70%, а галактик – еще больше. Как бы то ни было, эти данные постоянно уточняются, а новые технологии позволяют нам узнавать больше о нашей Вселенной.

#космос

#наука

#планета

#звезда

Больше новостей и самые свежие видео:

Наш Youtube

Наш Telegram

Тема: Законы Кеплера. Определение масс  небесных  тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

                                                      Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

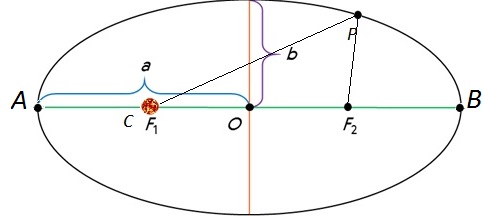
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

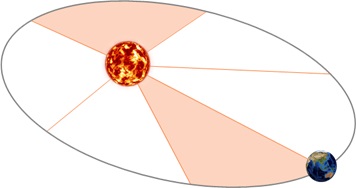
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

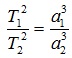
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

,

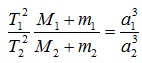где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ – соответственно массы их спутников.

Обобщённый третий закон  Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

,

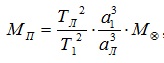где Т_л и α_л– период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

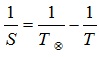
б) для внутренней планеты:

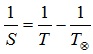
Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7.  Определить период обращения астероида Белоруссия если большая полуось его орбиты    а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

 

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.