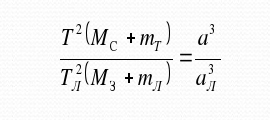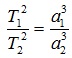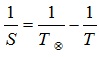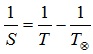Как найти массу планеты?
АстрономияПланетыМасса планет
Марина С.
11 февраля 2020 · 14,7 K
Я с детства хотел понять что за место такое Вселенная. Лишь с долгими годами усердных… · 13 апр 2020 ·
Все планеты взаимодействуют по Ньютоновской механике. В формулах есть М1 и М2 и еще масса других параметров. По скорости планеты, по её спутникам и расположении в звездной системе – по всем этим параметрам можно расчитать очень точно массу планеты. Это надо смотреть в конкретном случае, что нам известно и уже изсходить из этого, но в любом случае, это самое просто после определения скорости планеты и период обращения.
8,2 K
просверлить дыру до ядра измерить радиус замерить 1 см и умножить ту длину на компе обработать и вычислить вес
Комментировать ответ…Комментировать…
Неравнодушный человек, не терпящий несправедливости. · 11 февр 2020
Массу планеты можно найти 2-ми способами.
1-й подходит для планеты, когда известно ускорение свободного падения на её поверхности по формуле, выведенной из закона всемирного тяготения: M = g*R^2/G (где g-ускорение свободного падения, G-гравитационная постоянная R-радиус планеты);
2-й используется для планет имеющих спутник с массой заведомо много меньше массы самой… Читать далее
11,1 K
Комментировать ответ…Комментировать…
Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
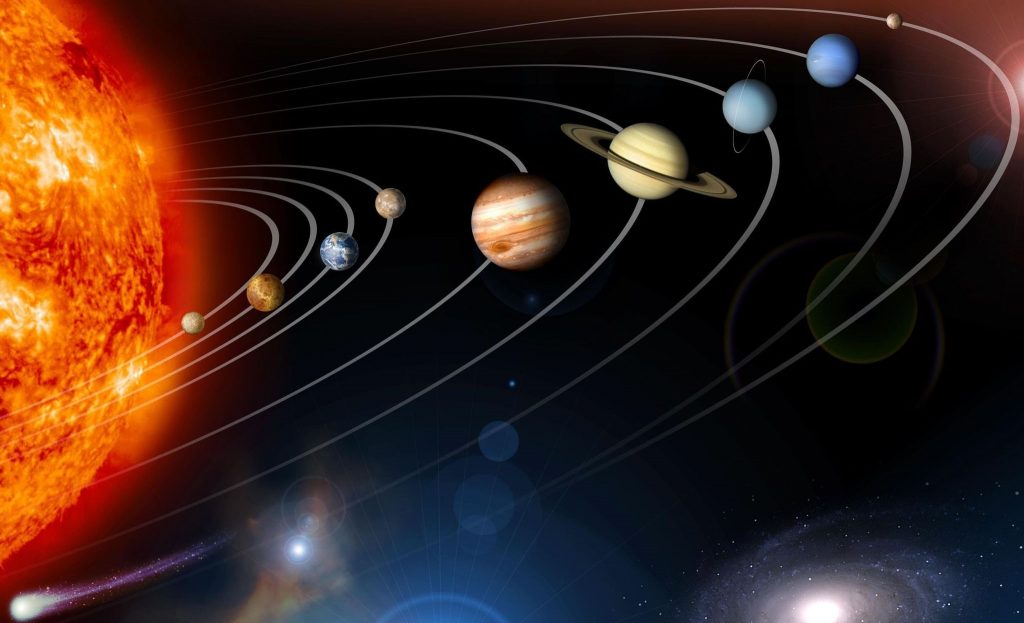
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?
Занимательная физика
Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.
Барометр и законы Ньютона
Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).
F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.
Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.
Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².
Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.
Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.
Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.
Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.
Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.
G = 6,67430(15)*10ˆ(-11) Н·м²·кг²
Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг.
Нейтрино
Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.
Испанские физики поставили лабораторию на Южном полюсе, дождались момента, когда Солнце окажется на Северном полюсе и выловили нейтрино с обратной стороны.
Эксперимент кажется фантастичным, однако измерив скорость частиц, прошедших сквозь Землю, физики нашли плотность планеты и, соответственно, массу.
Как измеряются далекие планеты?
Масса далеких планет вычисляется примерно. Основами для вычислений становятся орбиты планет, орбиты их спутников и гравитационные возмущения между ними.
Масса звезд вычисляется по степени их яркости. Считается, чем ярче небесное тело, тем оно массивнее. По светимости звезды определяется её химический состав, а значит примерная плотность и вес.
Как найти массу планеты зная радиус и ускорение свободного падения.
Если вам необходимо получить ответ на вопрос Как найти массу планеты зная радиус и ускорение свободного падения?, относящийся
к уровню подготовки учащихся 10 – 11 классов, вы открыли нужную страницу.
В категории Физика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
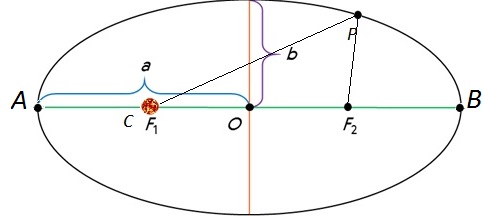
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
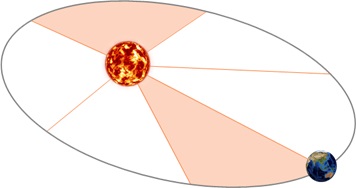
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
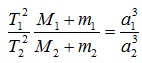
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 – соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
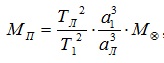
где Тл и αл– период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.