Как найти массу планеты в массах земли

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

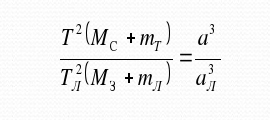
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Тема: Законы Кеплера. Определение масс  небесных  тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

                                                      Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

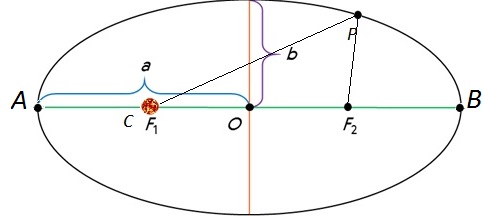
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

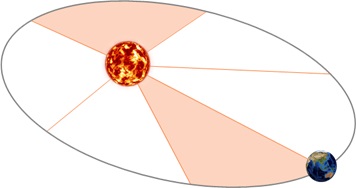
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

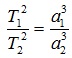
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

,

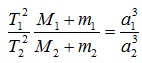где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ – соответственно массы их спутников.

Обобщённый третий закон  Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

,

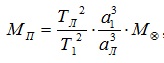где Т_л и α_л– период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

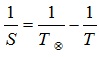
б) для внутренней планеты:

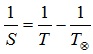
Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7.  Определить период обращения астероида Белоруссия если большая полуось его орбиты    а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Масса – это одно из самых важных свойств материи. Являясь мерой гравитационного взаимодействия, именно она во многом определяет облик нашей Вселенной – от звезд и планет до галактических скоплений. Однако, измерение этой величины в космических масштабах – совсем не простая задача. Так как же ученые узнают массы планет, звезд и других небесных тел?

Начнем с относительно простого – массы Земли. В качестве основы нам понадобится закон всемирного тяготения, сформулированный Исааком Ньютоном еще в 1666 году. Согласно ему, сила притяжения двух тел прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между объектами.

Из него легко можно вывести формулу для ускорения свободного падения. В свою очередь, находясь на Земле, эту величину можно измерить различными способами. Самый очевидный из них – сбросить с высокой башни тяжелый предмет и засечь время падения. Другой вариант – изготовить из нитки и грузика простейший маятник, после чего замерить период его колебаний. Если вам интересно попробовать провести этот несложный, но занимательный эксперимент самостоятельно – напишите об этом в комментариях, и мы обязательно посвятим ему одну из ближайших статей.

Радиус же нашей планеты также можно определить с довольно высокой точностью, не покидая ее – древние греки справлялись с этим еще три тысячи лет назад. Для этого потребуется две астролябии – так называется прибор для измерения высоты небесных тел на небосводе. Кроме того, необходим знакомый в другом городе, часы и любой способ связи. Нужно всего лишь одновременно измерить высоту солнца над горизонтом в полдень, после чего решить несложное уравнение.

Таким образом, зная радиус нашей планеты и ускорение свободного падения, можно рассчитать массу Земли. Разумеется, чем точнее будут измерены исходные данные, тем ближе к истине окажетсяконечный результат вычислений.

Прямым следствием из закона всемирного тяготения является третий закон Кеплера, связывающий орбиты и массы небесных тел. С его помощью можно узнать массу Луны, зная параметры ее орбиты и массу нашей планеты. Аналогично вычисляется масса Солнца, а от нее – всех остальных планет нашей системы.

С дальними же светилами все обстоит намного сложнее. Параметры двойных звезд относительно просто определяются по их взаимному движению, главное – правильно измерить расстояния. В случае же одиночных светил используются различные косвенные методы.

Например, на основе огромного количества наблюдений была сформулирована зависимость массы звезды от ее светимости. К сожалению, белые карлики и пульсары не подчиняются этой закономерности, и их параметры приходится определять иными методами.

Еще одним способом является спектральный анализ излучения звезды. Дело в том, что ее собственная гравитация искажает линии спектра подобно доплеровскому смещению. Массы экзопланет определяют по их влиянию на собственное движение материнского светила, а звездных скоплений – как сумму масс составляющих их объектов. Параметры же далеких галактик вычисляются либо по их вращению, либо по средней скорости собственного движения их компонентов.

Естественно, что чем дальше расположен объект от Земли, тем меньше точность, с которой можно вычислить его параметры. Например, масса нашей планеты определена с точностью 0,05%, Луны и Солнца – 0,1%, планет системы – до 0,7%. В то же время, погрешность измерения характеристик некоторых звезд может составлять от 20 до 70%, а галактик – еще больше. Как бы то ни было, эти данные постоянно уточняются, а новые технологии позволяют нам узнавать больше о нашей Вселенной.

#космос

#наука

#планета

#звезда

Больше новостей и самые свежие видео:

Наш Youtube

Наш Telegram