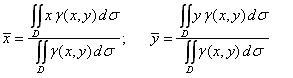3 Приложения
двойных интегралов
3.1 Теоретическое
введение
Рассмотрим приложения двойного интеграла
к решению ряда геометрических задач и
задач механики.
3.1.1 Вычисление площади и массы плоской
пластины
Рассмотрим тонкую материальную
пластину D,
расположенную в плоскости Оху.
Площадь
S
этой пластины может быть найдена с
помощью двойного интеграла по формуле:
|
|
(1) |
Пусть в каждой точке пластины
задана ее поверхностная плотность γ
= γ (x,
y) ≥ 0. Будем считать,
что функция γ = γ (x,
y) непрерывна в области
D.
Тогда масса
m
этой пластины равна двойному интегралу
от функции плотности γ (x,
y) по области D:
|
|
(2) |
3.1.2
Статические моменты. Центр масс плоской
пластины
Статическим моментом
Mx
относительно оси Ox
материальной точки P(x;y),
лежащей в плоскости Oxy
и имеющей массу m,
называется произведение массы точки
на ее ординату, т.е. Mx=
my. Аналогично
определяется статический момент My
относительно оси Oy:
My
= mx.
Статические
моменты плоской
пластины с поверхностной плотностью γ
= γ (x,
y) вычисляются по
формулам:
|
|
(3) |
|
|
(4) |
Как известно из механики,
координаты xc
, yc
центра масс плоской материальной системы
определяются равенствами:
|
|
(5) |
где m
– масса системы, а Mx
и My
– статические моменты системы. Масса
плоской пластины m
определяется формулой (1), статические
моменты плоской пластины можно вычислить
по формулам (3) и (4). Тогда, согласно
формулам (5), получаем выражение для
координат центра масс плоской пластины:
|
|
(6) |
3.2 Содержание
типового расчета
Типовой расчет содержит
две задачи. В каждой задаче задана
плоская пластина D,
ограниченная линиями, указанными в
условии задачи. Г(x,y)
– поверхностная плотность пластины D.
Для этой пластины найти:
1. S
– площадь;
2. m
– массу;
3. My
, Mx
– статические моменты относительно
осей Оy
и Ох
соответственно;
4.
![]() ,
,
![]() –
–
координаты центра масс.
3.3 Порядок
выполнения типового расчета
При решении каждой задачи
необходимо:
1. Выполнить чертеж заданной
области. Выбрать систему координат, в
которой будут вычисляться двойные
интегралы.
2. Записать область в виде
системы неравенств в выбранной системе
координат.
3. Вычислить площадь S
и массу m
пластины по формулам (1) и (2).
4. Вычислить
статические моменты My
, Mx
по формулам (3) и (4).
5. Вычислить
координаты центра масс
![]() ,
,
![]() по
по
формулам (6). Нанести центр масс на чертеж.
При этом возникает визуальный
(качественный) контроль полученных
результатов.
Численные ответы должны
быть получены с тремя значащими цифрами.
3.4 Примеры
выполнения типового расчета
Задача 1.
Пластина D
ограничена линиями: y
= 4 – x2;
х =
0; y
= 0 (x
≥ 0; y
≥ 0) Поверхностная плотность γ0
= 3.
Решение.
Область, заданная в задаче, ограничена
параболой y
= 4 – x2,
осями координат и лежит в первой четверти
(рис. 1). Задачу будем решать в декартовой
системе координат. Эта область может
быть описана системой неравенств:
![]()

Рис.
1
Площадь S
пластины равна (1):
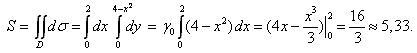
Так
как пластина однородная, ее масса m
= γ0S
= 3·![]()
= 16.
По формулам (3), (4) найдем статические
моменты пластины:
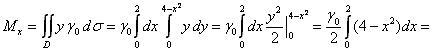



Координаты
центра масс находятся по формуле (6):


Ответ:
S ≈
5,33; m
= 16; Mx
= 25,6; My
= 12;
![]() =
=
0,75;
![]() =
=
1,6.
Задача 2.
Пластина D
ограничена линиями: х2
+ у2
= 4; х
= 0, у
= х
( х
≥ 0, у
≥ 0). Поверхностная плотность γ(x,y)
= у.
Решение.
Пластина ограничена окружностью и
прямыми, проходящими через начало
координат (рис. 2). Поэтому для решения
задачи удобно использовать полярную
систему координат. Полярный угол φ
меняется от π/4 до π/2. Луч, проведенный
из полюса через пластину, «входит» в
неё при ρ = 0 и «выходит» на окружность,
уравнение которой: х2
+ у2
= 4 <=> ρ = 2.

Рис.
2
Следовательно, заданную
область можно записать системой
неравенств:

Площадь
пластины найдем по формуле (1):
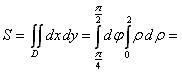

Массу
пластины найдем по формуле (2), подставив
γ(x,y)
= у = ρ
sinφ:
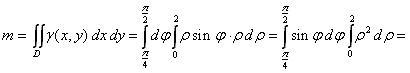

Для
вычисления статических моментов пластины
используем формулы (3) и (4):




Координаты
центра масс получим по формулам (6):
![]()
Ответ:
S ≈
1,57; m
≈ 1,886; Mx
= 2,57; My
= 1;
![]() =
=
0,53;
![]() =
=
1,36.
3.5 Оформление
отчета
В отчете должны быть представлены все
выполненные расчеты, аккуратно выполненные
чертежи. Численные ответы должны быть
получены с тремя значащими цифрами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
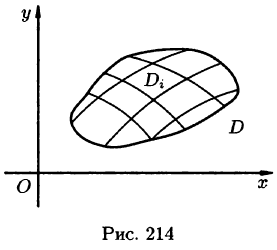
Пусть в замкнутой облас ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»
ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»  площади которых обозначим через
площади которых обозначим через  а диаметры (наибольшее расстояние между точками области) — через
а диаметры (наибольшее расстояние между точками области) — через 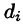 (см. рис. 214).
(см. рис. 214).
В каждой области  выберем произвольную точку
выберем произвольную точку 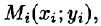 умножим значение
умножим значение 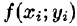 функции в этой точке на
функции в этой точке на 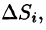 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
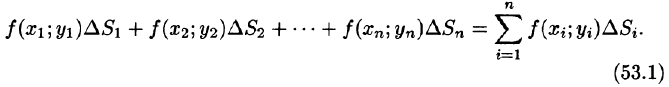
Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 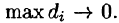 Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
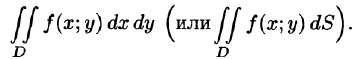
Таким образом, двойной интеграл определяется равенством
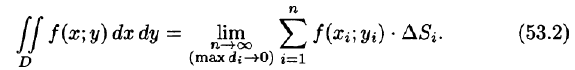
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
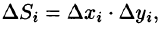 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде
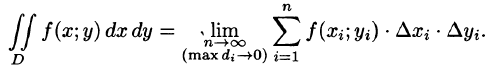
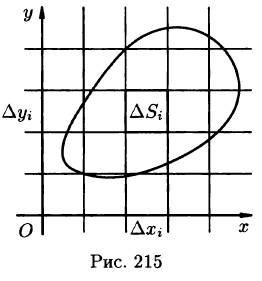

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью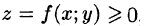 , снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей
, снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей  , площади которых равны A
, площади которых равны A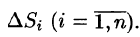 Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием
Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием  через
через 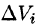 , получим
, получим
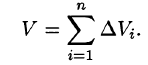
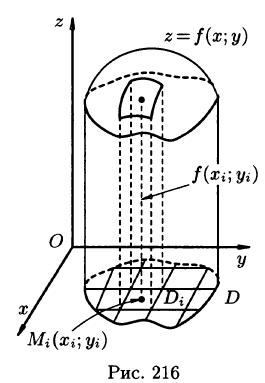
Возьмем на каждой площадке Di произвольную точку 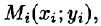 и заменим каждый столбик прямым цилиндром с тем же основанием
и заменим каждый столбик прямым цилиндром с тем же основанием  и высотой
и высотой 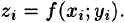 Объем этого цилиндра приближенно равен объему
Объем этого цилиндра приближенно равен объему 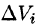 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 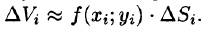 Тогда получаем:
Тогда получаем:
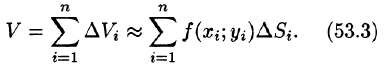
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей»  ,. Естественно принять предел суммы (53.3) при условии, что число площадок
,. Естественно принять предел суммы (53.3) при условии, что число площадок  неограниченно увеличивается
неограниченно увеличивается 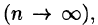 а каждая площадка стягивается в точку
а каждая площадка стягивается в точку 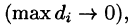 за объем V цилиндрического тела, т. е.
за объем V цилиндрического тела, т. е.
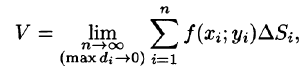
или, согласно равенству (53.2),
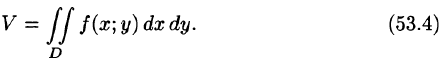
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 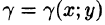 есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей
есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей 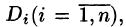 площади которых обозначим через
площади которых обозначим через 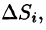 . В каждой области
. В каждой области  возьмем произвольную точку
возьмем произвольную точку 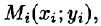 и вычислим плотность в ней:
и вычислим плотность в ней: 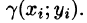
Если области D, достаточно малы, то плотность в каждой точке 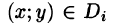 мало отличается от значения
мало отличается от значения 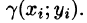 Считая приближенно плотность в каждой точке области
Считая приближенно плотность в каждой точке области  постоянной, равной
постоянной, равной 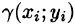 , можно найти ее массу
, можно найти ее массу 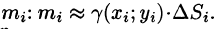 Так как масса m всей пластинки D равна
Так как масса m всей пластинки D равна 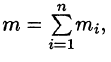 Для ее вычисления имеем приближенное равенство
Для ее вычисления имеем приближенное равенство
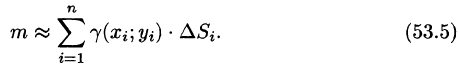
Точное значение массы получим как предел суммы (53.5) при условии 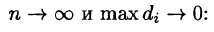
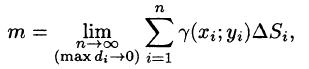
или, согласно равенству (53.2),
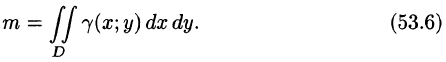
Итак, двойной интеграл от функции 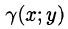 численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию 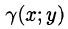 считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
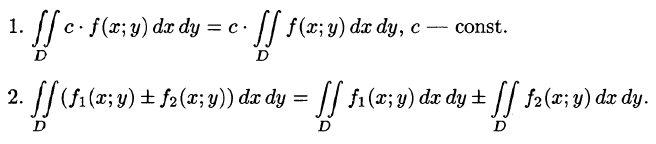
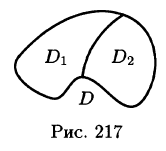
3.Если область D разбить линией на две области 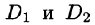 такие, что
такие, что 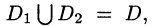 а пересечение
а пересечение 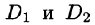 состоит лишь из линии, их разделяющей (см. рис. 217), то
состоит лишь из линии, их разделяющей (см. рис. 217), то
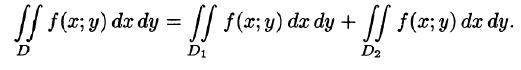
4.Если в области D имеет место неравенство 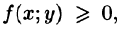 то и
то и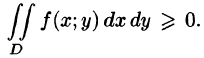 Если в области D функции f(x;y) и
Если в области D функции f(x;y) и 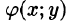 удовлетворяют неравенству
удовлетворяют неравенству 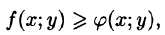 то и
то и
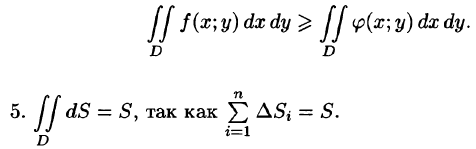
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 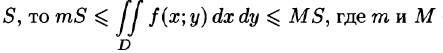 — соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
— соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка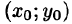 , что
, что 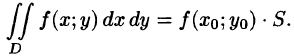 Величину
Величину
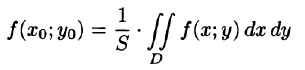
называют средним значением функции f(x; у) в области D.
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 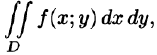 где функция
где функция  непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
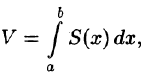
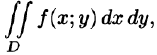
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми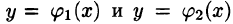 , причем функции
, причем функции 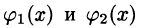 непрерывны и таковы, что
непрерывны и таковы, что 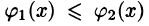 для всех
для всех 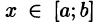 (см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
(см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси 
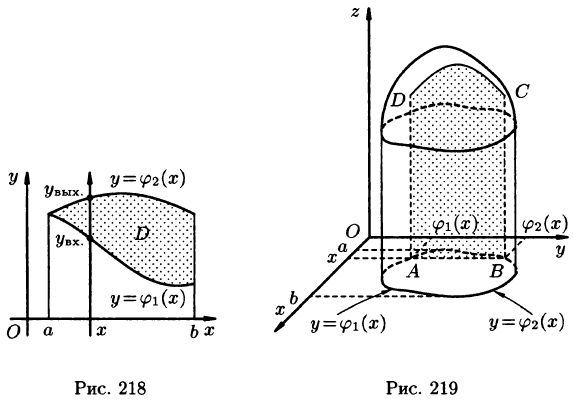
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
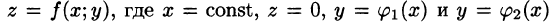
(см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
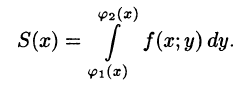
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
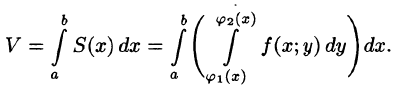
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 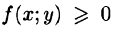 по области D. Следовательно,
по области D. Следовательно,
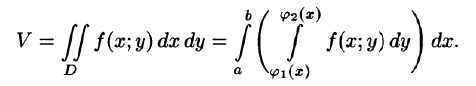
Это равенство обычно записывается в виде
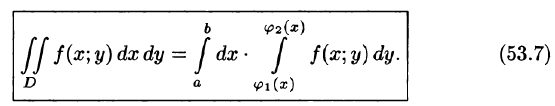
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 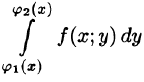 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 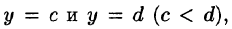 кривыми
кривыми
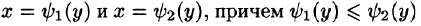
для всех 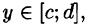 т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
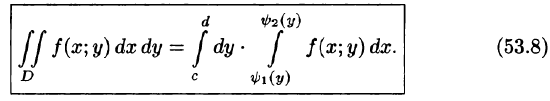
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
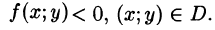
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 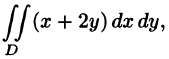 где область D ограничена линиями у
где область D ограничена линиями у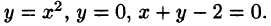
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
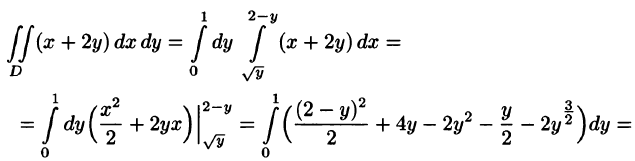
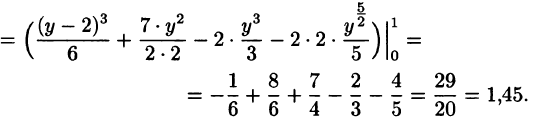
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 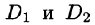 . Получаем:
. Получаем:
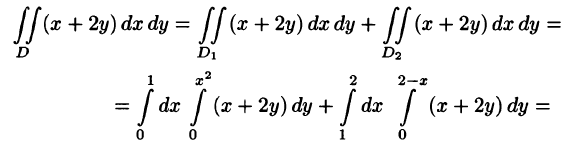
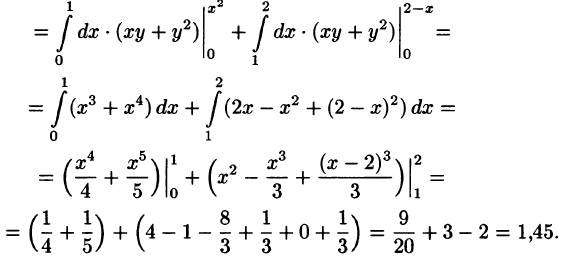
Ответ, разумеется, один и тот же.
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
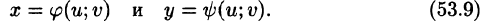
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
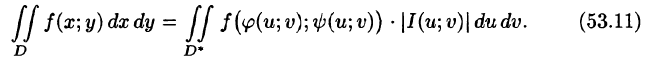
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
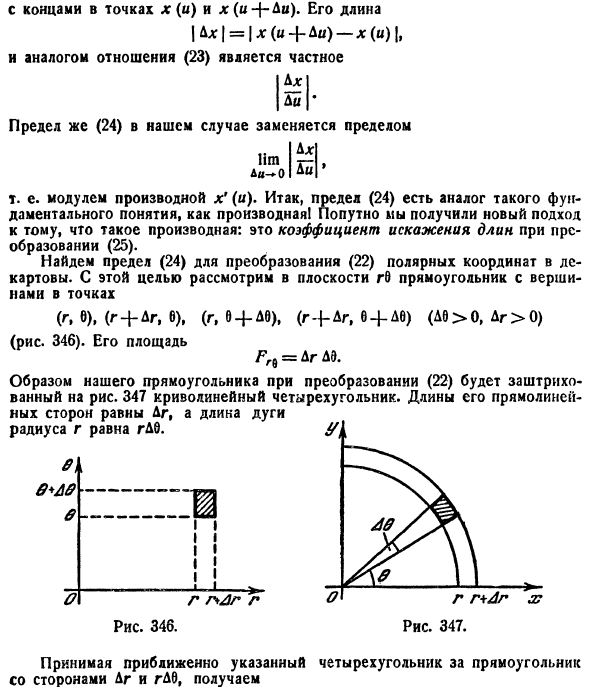
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами 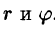
В качестве инь возьмем полярные координаты 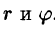 Они связаны с декартовыми координатами формулами
Они связаны с декартовыми координатами формулами 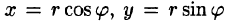 (см. п. 9.1).
(см. п. 9.1).
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
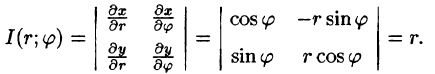
Формула замены переменных (53.11) принимает вид:
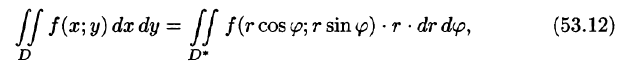
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами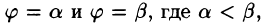 и кривыми
и кривыми 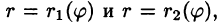 где
где 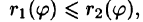 т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
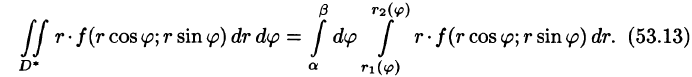
Внутренний интеграл берется при постоянном 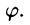
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
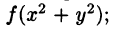 область D есть круг, кольцо или часть таковых.
область D есть круг, кольцо или часть таковых. - На практике переход к полярным координатам осуществляется путем замены
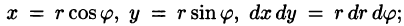 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по  (исследуя закон изменения
(исследуя закон изменения  точки
точки 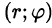 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 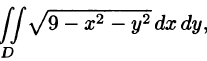 где область D — круг
где область D — круг 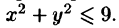
Решение: Применив формулу (53.12), перейдем к полярным координатам:
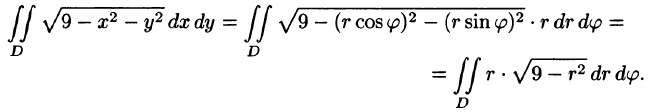
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 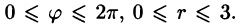 Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
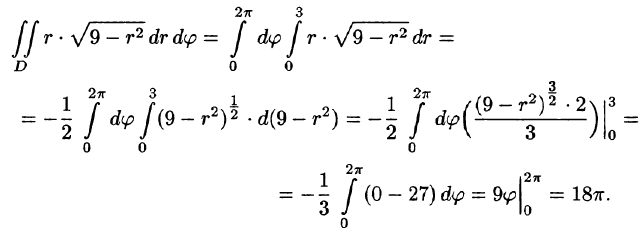
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
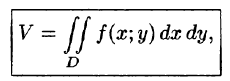
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
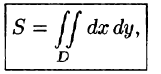
или, в полярных координатах,
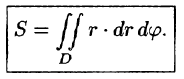
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 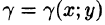 находится по формуле
находится по формуле
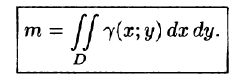
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
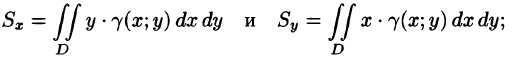
а координаты центра масс фигуры по формулам
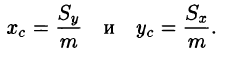
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 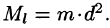 Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
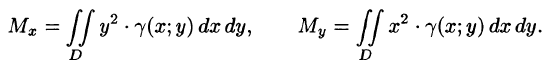
Момент инерции фигуры относительно начала координат — по формуле 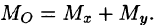
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
Найти объем тела, ограниченного поверхностями
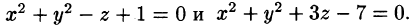
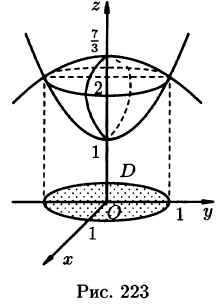
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
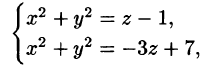
находим уравнение линии их пересечения:
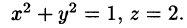
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 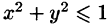 ) и ограниченных сверху соответственно поверхностями
) и ограниченных сверху соответственно поверхностями 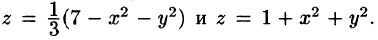 Используя формулу (53.4), имеем
Используя формулу (53.4), имеем
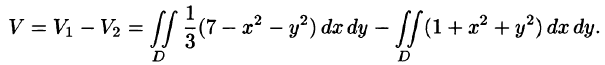
Переходя к полярным координатам, находим:
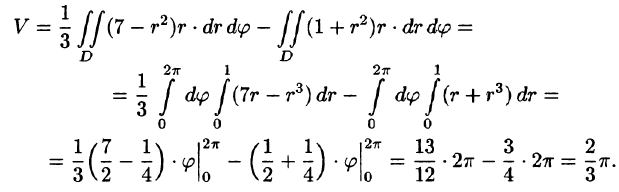
Пример:
Найти массу, статические моменты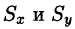 и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом
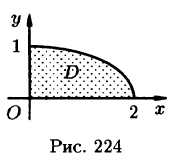
и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 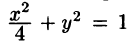 и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
Решение: По формуле (53.6) находим массу пластинки. По условию, 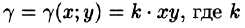 — коэффициент пропорциональности.
— коэффициент пропорциональности.
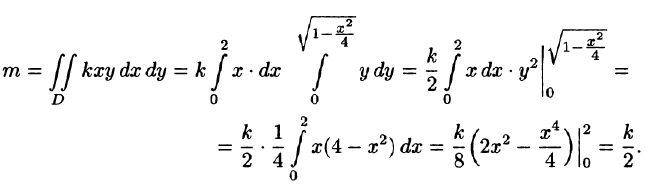
Находим статические моменты пластинки:
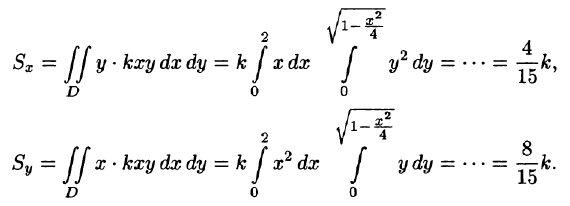
Находим координаты центра тяжести пластинки, используя формулы
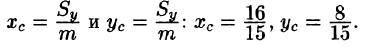
Двойной интеграл













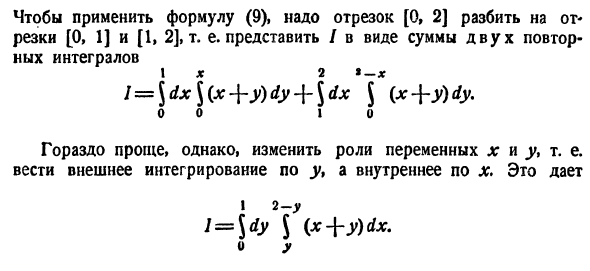

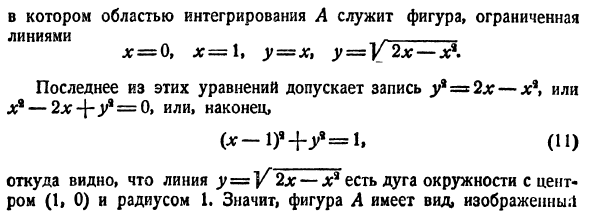















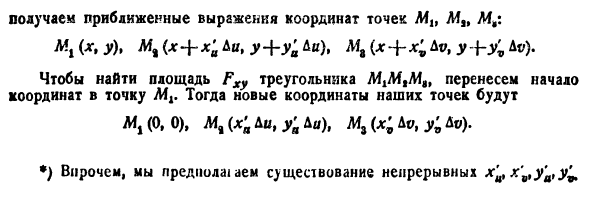





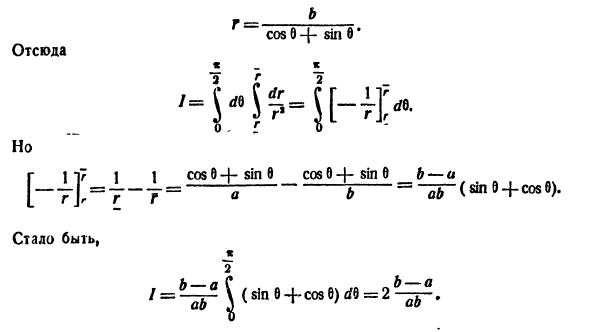






Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Механические приложения двойного интеграла
Будем считать, что $mathbf { textit { D } } $ – неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $mu (P)$. В механике $mu (P)$ определяется так. Точка $P$ окружается малой областью $mathbf { textit { S } } $, находится масса $mathbf { textit { m } } (mathbf { textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $mathbf { textit { S } } $ } и $mu (P)=mathop { lim } limits_ { diam(S)to 0 } frac { m(S) } { S } $. 
Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $mathbf { textit { D } } $ на малые подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } $,$mathbf { textit { D } } _ { 3 } , { ldots } , mathbf { textit { D } } _ { n } $, в каждой из подобластей $mathbf { textit { D } } _ { i } $ выберем произвольную точку $mathbf { textit { P } } _ { i } $, и, считая что в пределах $mathbf { textit { D } } _ { i } $ плотность постоянна и равна $mu (P_i )$, получим, что масса $mathbf { textit { D } } _ { i } $ приближённо есть $mu (P_i )cdot s(D_i )$, а масса всей пластины $sumlimits_ { i=1 } ^n { mu (P_i )cdot s(D_i ) } $.
Это интегральная сумма, при уменьшении $d=mathop { max } limits_ { i=1,2,ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=mathop { lim } limits_ { begin{array} { l } dto 0 \ (nto infty ) \ end{array} } sumlimits_ { i=1 } ^n { mu (P_i )cdot Delta s(D_i ) } =iintlimits_D { mu (P)ds } $.
Аналогично находятся другие параметры пластины:
Координаты центра тяжести
$x_c =frac { 1 } { m(D) } iintlimits_D { xcdot mu (P)ds } $, $y_c =frac { 1 } { m(D) } iintlimits_D { ycdot mu (P)ds } $;
Моменты инерции пластины
- $I_x =iintlimits_D { y^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Ox } } $ } ,
- $I_y =iintlimits_D { x^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Oy } } $ } ,
- $I_O =iintlimits_D { (x^2+y^2)cdot mu (P)ds } =I_x +I_y $ { относительно начала координат } .
Пластина расположена в области (R) и ее плотность в точке ( { left( { x,y }right) } ) равна ( { rho left( { x,y }right) } ).
Масса пластины
(m = largeiintlimits_Rnormalsize { rho left( { x,y }right)dA } )
Статические моменты пластины
Момент пластины относительно оси (Ox) определяется формулой
( { M_x } = largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } )
Аналогично, момент пластины относительно оси (Oy) выражается в виде
( { M_y } = largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } )
Координаты центра масс пластины
- (bar x = largefrac { { { M_y } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } = largefrac { { iintlimits_R { xrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize,;)
- (bar y = largefrac { { { M_x } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } = largefrac { { iintlimits_R { yrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize ).
Заряд пластины
(Q = largeiintlimits_Rnormalsize { sigma left( { x,y }right)dA } ),
где электрический заряд распределен по области (R) и его плотность в точке ( { left( { x,y }right) } ) равна ( { sigma left( { x,y }right) } ).
Среднее значение функции
(mu = largefrac { 1 } { S } iintlimits_Rnormalsize { fleft( { x,y }right)dA } ,;) где (S = largeiintlimits_Rnormalsize { dA } ).
Пример 1
Найти параметры неоднородной плоской пластины, ограниченной кривыми
$D:left[{ begin{array} { l } y=x^2, \ y=4; \ end{array} }right.$ если плотность $mu (x,y)=y+1$.
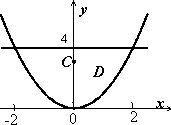
Решение:
$m(D)=iintlimits_D { (y+1)dxdy } =2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =$ $ =2intlimits_0^2 { left( { 12-x^4/2-x^2 }right)dx } =2left. { left( { 12x-x^5/10-x^3/3 }right) }right|_0^2 =2left( { 24-frac { 16 } { 5 } -frac { 8 } { 3 } }right)=frac { 544 } { 15 } . $ $ x_c =frac { 1 } { m(D) } iintlimits_D { x(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { x(y+1)dy } =frac { 15 } { 544 } intlimits_ { -2 } ^2 { xleft. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } = $ $=frac { 15 } { 544 } intlimits_ { -2 } ^2 { left( { 12x-x^5/2-x^3 }right)dx } = quad =frac { 1 } { 544 } left. { left( { 6x^2-x^6/10-x^4/4 }right) }right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ begin{array} { l } y_c =frac { 1 } { m(D) } iintlimits_D { y(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { y(y+1)dy } =frac { 15 } { 272 } intlimits_0^2 { left. { left( { y^3/3+y^2/2 }right) }right|_ { x^2 } ^4 dx } = \ =frac { 15 } { 272 } intlimits_0^2 { left( { 64/3+8-x^6/3-x^4/2 }right)dx } =frac { 15 } { 272 } left. { left( { 88x/3-x^7/21-x^5/10 }right) }right|_0^2 =frac { 15 } { 272 } left( { frac { 176 } { 3 } -frac { 128 } { 21 } -frac { 16 } { 5 } }right)=frac { 15 } { 272 } cdot frac { 1728 } { 35 } approx 2,72. \ end{array} $ $ I_x =iintlimits_D { y^2(y+1)dx } dy=2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { y^2(y+1)dy } =2intlimits_0^2 { left. { left( { y^4/4+y^3/3 }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { left( { frac { 256 } { 3 } -frac { x^8 } { 4 } -frac { x^6 } { 3 } }right)dx } = $ $ =2left. { left( { frac { 256 } { 3 } x-frac { x^9 } { 36 } -frac { x^7 } { 21 } }right) }right|_0^2 approx 300,7. $ $ I_y =iintlimits_D { x^2(y+1)dx } dy=2intlimits_0^2 { x^2dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { x^2left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { x^2left( { 12-frac { x^4 } { 2 } -x^2 }right)dx } = $ $ =2left. { left( { 4x^3-frac { x^7 } { 14 } -frac { x^5 } { 5 } }right) }right|_0^2 approx 32,9. quad I_O =iintlimits_D { left( { x^2+y^2 }right)(y+1)dx } dy=I_x +I_y approx 333,6. $
Пример 2
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $rho left( { x,y }right) = xy.$
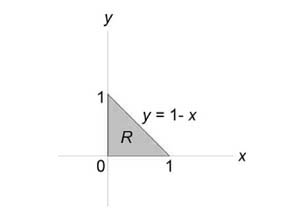
Решение:
Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = iintlimits_R { { y^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^3 } dy } }right]xdx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^4 } } } { 4 } }right) }right|_0^ { 1 – x } }right]xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { { { left( { 1 – x }right) } ^4 } xdx } } = { frac { 1 } { 4 } intlimits_0^1 { left( { 1 – 4x + 6 { x^2 } – 4 { x^3 } + { x^4 } }right)xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { left( { x – 4 { x^2 } + 6 { x^3 } – 4 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 4 } left. { left( { frac { { { x^2 } } } { 2 } – frac { { 4 { x^3 } } } { 3 } + frac { { 6 { x^4 } } } { 4 } – frac { { 4 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 4 } left( { frac { 1 } { 2 } – frac { 4 } { 3 } + frac { 3 } { 2 } – frac { 4 } { 5 } + frac { 1 } { 6 } }right) } = { frac { { 49 } } { { 120 } } . } $
Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = iintlimits_R { { x^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { x^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { ydy } }right] { x^3 } dx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^2 } } } { 2 } }right) }right|_0^ { 1 – x } }right] { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { { { left( { 1 – x }right) } ^2 } { x^3 } dx } } = \ = { frac { 1 } { 2 } intlimits_0^1 { left( { 1 – 2x + { x^2 } }right) { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { left( { { x^3 } – 2 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 2 } left. { left( { frac { { { x^4 } } } { 4 } – frac { { 2 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 2 } left( { frac { 1 } { 4 } – frac { 2 } { 5 } + frac { 1 } { 6 } }right) } = { frac { 1 } { { 120 } } . } $
Пример 3
Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $sigma left( { x,y }right) = 1 + { x^2 } + { y^2 } ;left( { text { Кл/м } ^2 }right)$ Вычислить полный заряд диска.
Решение:
В полярных координатах область, занятая диском, описывается множеством (left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].)
Полный заряд будет равен $ { Q = iintlimits_R { sigma left( { x,y }right)dxdy } } = { intlimits_0^ { 2pi } { left[ { intlimits_0^1 { left( { 1 + { r^2 } { { cos } ^2 } theta + { r^2 } { sin^2 } theta }right)rdr } }right]dtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { left( { 1 + { r^2 } }right)rdr } } = { 2pi intlimits_0^1 { left( { r + { r^3 } }right)dr } } = \ = { 2pi left. { left( { frac { { { r^2 } } } { 2 } + frac { { { r^4 } } } { 4 } }right) }right|_0^1 } = { 2pi left( { frac { 1 } { 2 } + frac { 1 } { 4 } }right) } = { frac { { 3pi } } { 2 } ;left( { text { Кл } }right). } $
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Особенности перевода в другой ВУЗ
1 ставка
Помогите решить задачи в Excel
1 ставка
Основные понятия и законы химии.
Билет №3
Помоги пожалуйста срочно!!!!!!!!!!!
1 ставка
Реставрационно-художественный колледж СПб
1 ставка
Вопрос по физике
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Mr Bill
Профи
(894),
закрыт
1 год назад
Лучший ответ
Amaxar 777
Высший разум
(104907)
1 год назад
Просто двойной интеграл по всей пластинке, умноженный на плотность.
Mr BillПрофи (894)
1 год назад
То есть так?
Amaxar 777
Высший разум
(104907)
Ага
Остальные ответы
Похожие вопросы