Срочно! Помогите решить! Физика
Пётр Ушаков
Знаток
(439),
закрыт
1 год назад
Куклин Андрей
Высший разум
(189239)
2 года назад
Натяжение нити T=21 Н. Определите массу груза m. m = T/g = 21/9,8 = 2,14 кг.
“К правому концу рычага дополнительно подвесили груз массы M=1.4 кг.” –
(m*g – T2)*7 = M*g*3. T2 = m*g – 3*M*g/7 = 2.1*10 – 3*1,4*10/7 = 15 H.
“На какое расстояние в сторону груза M надо сместить груз m,” –
m*g*(7 – x) = M*g*3
x = (7*m*g – 3*M*g)/m*g = 5.
На 50 см.
Владислав КорепановУченик (176)
2 года назад
Под первой цифрой немного неправильно
Куклин Андрей
Высший разум
(189239)
Владислав Корепанов, Что g = 10 не заметил.
Что за первая цифра?
Сила, которая передается по длине гибкой среды, такой как веревка, кабель, веревка и т. Д., Когда ее тянут или подвешивают силой, действующей на тяжелый объект, называется сила натяжения. В этой статье мы изучим как рассчитать силу натяжения.
Узнайте больше о Что такое частота колебаний
Расчет силы натяжения
Подсчитаем сила натяжения учитывая массу объекта «m» и объекта ускорения «a».
от Второй закон движения Ньютона, мы знаем это
F = m * a
Здесь сила называется сила натяжения так что уравнение становится,
Т = м * а
Случай (i): пусть вес объекта (w) действует вниз, а сила натяжения (T) на веревке, действующая вверх, и ускорение свободного падения равно «g».

Тогда сила натяжения будет рассчитана как
Т = Ш
Но мы знаем W = m * g
т.е. T = m * g
Случай (ii): когда объект с определенным ускорение в направлении вниз вес объекта больше, чем натяжение, тогда уравнение принимает следующий вид:
W – T = ma
Но W = m * g,
(м * г) – Т = т * а
Т = м * г – м * а
Или T = m (g – a)
Случай (iii): теперь тело ускоряется в направлении вверх, и вес должен быть меньше напряжения. Тогда уравнение становится,
Т – Ж = м * а
Т – (m * g) = m * a
Т = м * г + м * а
Или T = m (g + a)
Случай (iv): сила натяжения зависит не только от массы объекта и ускорения, но и от угла подвески. Когда объект массой «m» подвешен вертикально под углом θ, силу натяжения можно рассчитать, как показано ниже.

Здесь всего одна струна, а разрешающая сила направлена по оси Y.
Т = м * г
Т sin (θ) = m * g
Сходным образом ; когда объект зажат двумя массами горизонтально и составляет угол θ1 и θ2 тогда сила натяжения будет
T1 потому что (θ) = Т2 соз (θ)

Узнайте больше о Примеры центробежной силы
Узнайте больше о Трение – консервативная сила
Некоторые решенные примеры
С нижнего конца фонаря свисает предмет массой 24 кг. нерастяжимый кабель. Если верхний конец троса прикреплен к крыше с помощью крючка, то рассчитать силу натяжения, действующую на трос?
Решение:
Дано: масса объекта = 24 кг.
Ускорение свободного падения = 9.8 м / с
Поскольку объект просто подвешен на крыше и нет движения объекта. Следовательно, сила натяжения, действующая на струну, равна весу объекта.
Т = W = мг = 24 × 9.8
= 235.20 Н
Узнайте больше о Примеры простых гармоник
Рассчитайте массу объекта, когда его тянут за веревку, и объект движется вниз с ускорением 8 м / с.2. Если сила натяжения, действующая на канат, составляет 286 Н. (Примите ускорение свободного падения как 10 м / с.2).
Решение:
Дано: Сила натяжения, действующая на трос = 286Н
Ускорение объекта, действующего в нисходящем направлении = 8 м / с2
Ускорение свободного падения = 10 м / с2
Мы знаем, что для объекта, ускоряющегося в направлении вниз, сила натяжения определяется выражением
Т = мг – ма
Рассчитать массу объекта; переставляя уравнение, мы получаем
Т = м (г – а)


Объект массой 9 кг подвешен на тросе, ускоряющемся вверх. Если сила натяжения, действующая на него, составляет 143 Н, то узнайте ускорение объекта, действующего в восходящем направлении. (Примите ускорение свободного падения как 10 м / с.2).
Решение:
Дано: масса объекта = 9 кг.
Сила натяжения = 143Н
Ускорение свободного падения = 10 м / с2
Мы знаем, что сила натяжения, действующая на объект, когда он ускоряется вверх, равна
Т = мг + ма
143N = (9 кг × 10) + (9 кг × а)
143N = 90 + (9 × а)
143 – 90 = 9a
53 = 9а

a = 5.888 м / с2
К кайту прикреплена тетива, которая образует угол 35 °. За веревку никто не тянет и не тянет. Действующая чистая сила составляет 60 Н. рассчитать натяжение струны.
Решение:
Дано: угол подвеса = 35 °
Чистая сила = м * г = 60 Н
T sin (35) = 60
Т (0.5735) = 60

Т = 104.620 Н
Часто задаваемые вопросы :
Почему работа, проделанная напряжением, всегда нулевая, объяснять?
Ответ: Работа, проделанная чем-либо, дается
Вт = ФС
Где F – сила, а S – смещение
Это означает, что проделанная работа зависит как от силы, так и от смещения. Но напряжение – это сила, в которой не будет смещения.
т.е. S = 0
W = F × 0
W = 0
Следовательно, работа, совершаемая силой натяжения, всегда будет равна нулю.
Сила натяжения – это контактная сила, объясните?
Ответ: Контактная сила – это сила, прилагаемая двумя объектами, находящимися в контакте друг с другом. В силе натяжения сила передается через трос, веревку или жало, когда они туго натягиваются силами, действующими противоположно друг другу. Между передающей средой и объектом существует контакт. Таким образом, сила натяжения – это сила контакта.
Как сила тяжести влияет на силу натяжения?
Ответ: Сила натяжения всегда действует в направлении, противоположном гравитационному притяжению. Если объект висит, он должен быть уравновешен силой натяжения, иначе он должен будет ускоряться в направлении вниз под действием силы тяжести.
Как напряжение зависит от массы?
Ответ: Когда объект подвешивается на веревке, веревке или тросе, возникает только натяжение. Понятно, что когда веревка не тянет за собой какой-либо предмет, натяжение веревки не возникает. Таким образом, напряжение всегда пропорционально массе объекта.
Когда объект определенной массы m тянется с помощью веревки человеком A. Человек B тянет тот же объект в противоположном направлении, то какой будет сила натяжения, действующая на веревку человека A?
Ответ: Из уравнения силы натяжения; сила натяжения, действующая на сторону человека А, равна
TA = м * а
Сила натяжения со стороны человека B равна
TB = м * а
Чистая сила будет
Fсеть = ТA – ТB
Поскольку сила TB действует в направлении, противоположном TB
Преобразуя приведенное выше уравнение, мы получаем натяжение веревки A.
TA = Фсеть + TB

![]()
Очень надо!
И можно, пожалуйста, с объяснением
К рычагу подвесили груз и прикрепили нить так, как показано на рисунке. (см. рисунок) Сила натяжения нити равна 6 Н. Найдите массу груза. Ответ дайте в кг

Остались вопросы?
Новые вопросы по предмету Физика
Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
(F=F_{тяж}=m*g)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
(F_n=m*g*cos(a))
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
(F=F_{тяж}+m*a)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
(F=frac{mtimes nu ^{2}}{r})
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
(H=frac{kgtimes m}{c^{2}})
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
(bar{T}+mbar{g}=mbar{a})
(bar{T}) является силой натяжения нити.
Проекция уравнения будет иметь следующий вид:
(T – mg = ma)
Данное выражение позволяет рассчитать ускорение:
(a=frac{T-mg}{m})
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
(a=frac{4400-4*9,8}{400})
Ответ: a = 1.2 (м/с^2)
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
(bar{T}+mbar{g}=mbar{a})
Проекции данной формулы по осям определяются следующим образом:
X: (T sin α = ma = mω2R)
Y: (-mg + T cos α = 0)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
(T=frac{mg}{cos alpha })
Анализ рисунка позволяет вывести следующее уравнение:
(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))
Ответ: Т=1,225 H
Два тела связаны невесомой и нерастяжимой нитью, перекинутой через блок, подвешенный на пружинных весах (динамометре). Найти массы тел, их ускорения и силу натяжения нити, если известно, что масса первого тела в 2 раза меньше массы второго, а показание пружинных весов – 56 Н.
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: Два тела связаны невесомой и нерастяжимой нитью, перекинутой через блок, подвешенный на пружинных весах (динамометре)
| Масса первого тела | $m_{1}$ | ||
|---|---|---|---|
| Масса второго тела | $m_{2}$ | {2m_{1}} | |
| Показание пружинных весов | F | 56 | Н |
| Ускорение тел | $a$ | ? | |
| Сила натяжения нити 1 | $T_{1}$ | ? | |
| Сила натяжения нити 2 | $T_{2}$ | ? |
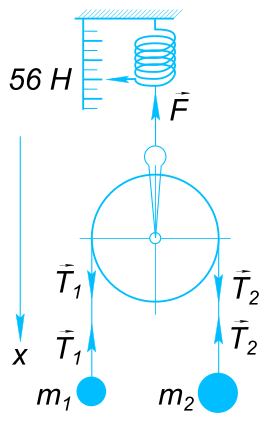
Изобразим на рисунке условия задачи
На тело массой m1 действует сила тяжести
$ vect{m_{1}g} $
и сила натяжения нити
$ vect{T_{1}} $
На тело массой m2 действует сила тяжести
$ vect{m_{2}g} $
и сила натяжения нити
$ vect{T_{2}} $
На блок действует силы натяжения нитей
$ vect{T_{1}} и vect{T_{2}} $
и сила упругости пружины динамометра
$ vect{F} $
Направим ось x вертикально вниз и запишем уравнение движения каждого тела в проекциях на данную ось
$ m_{1}g – T_{1} = – m_{1}a_{1} $
$ m_{2}g – T_{2} = m_{2}a_{2} $
$ T_{1} + T_{2} – F = 0 $
Если принять массу блока равной нулю, а нить невесомой и не растяжимой, то
$ |vect{T_{1}}| = |vect{T_{2}}|=T $
и
$ a_{1} = a_{2} = a $
Тогда уравнения примут вид
$ m_{1}g – T = – m_{1}a $
$ 2m_{1}g – T = 2m_{1}a $
$ 2T – F = 0 $
Откуда находим
$ T = frac{F}{2} = frac{56}{2} = 28 Н $
Приравняв
$ m_{1}(g+a) = 2m_{1}(g-a) $
Откуда, раскрыв скобки, находим
$ a = frac{g}{3} = frac{9,81}{3} = 3,3 frac{м}{с^{2}} $
и
$ m_{1} = frac{T}{g+a} = frac{T}{g+frac{g}{3}} = frac{3T}{4g} = frac{3×28}{4×9,81} = 2,14 кг $
$ m_{2} = 2m_{1} =2×2,14 =4,28 кг $
Ответ:
$ Ускорение тел 3,3 frac{м}{с^{2}}, масса тел 2,14 кг и 4,28 кг $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
