Как определить массу тела, зная силу тяжести и ускорение свободного падения?
Найдите правильный ответ на вопрос ✅ «Как определить массу тела, зная силу тяжести и ускорение свободного падения? …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Физика » Как определить массу тела, зная силу тяжести и ускорение свободного падения?
Как найти массу если известна сила и следовательно ускорение свободного падения.
На этой странице сайта вы найдете ответы на вопрос Как найти массу если известна сила и следовательно ускорение свободного падения?,
относящийся к категории Физика. Сложность вопроса соответствует базовым
знаниям учеников 5 – 9 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.
Вес тела. Калькулятор онлайн.
Калькулятор вычисления веса тела, вычислит вес тела, массу, ускорение свободного падения и даст подробное решение.
Калькулятор содержит:
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
В данной таблице приведены значения ускорения свободного падения для планет Солнечной системы и их спутников.
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Вес тела P, которое покоится в инерциальной системе отсчета равен произведению массы m этого тела и ускорения свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единицей измерения силы – Ньютон (Н, N)
Масса m =
Ускорение свободного падения g =
Единица измерения веса P
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Масса тела m равна отношению веса P к ускорению свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единица массы – килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.
Вес P =
Ускорение свободного падения g =
Единица измерения массы m
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
Ускорение свободного падения g равно отношению веса тела P к его массе m.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Ускорение свободного падения — это ускорение, которое тело приобретает под действием гравитационной силы около поверхности небесных тел в космическом пространстве.
Единица ускорения – метр в секунду в квадрате.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
 Движение спутников
Движение спутников
Ускорение свободного падения
Первая космическая скорость
Вторая космическая скорость
«Звездная» болезнь — дело опасное, но излечимое. Начинать советую с этой статьи.
Еще в 17 веке Ньютон открыл закон всемирного тяготения, а в 21 веке кто-то еще верит, что Земля плоская.
Каждый пусть решит сам для себя, какая же на самом деле Земля, а я по старинке буду думать, что она круглая.
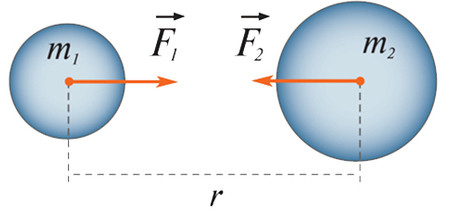
По закону всемирного тяготения сила притяжения двух тел:
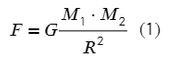
G = 6,67×10⁻¹¹ − (гравитацоинная постоянная),
R − расстояние между центрами двух тел,
M₁ и M₂ − массы тел.
Мы знаем, что сила тяжести находится как
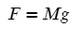
Приравняем выше приведенные формулы, немного «покрутим» их и получим, что свободное падение для любой планеты можно найти, зная ее массу и радиус:
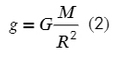
А если еще вспомнить второй закон ньютона и ускорение для центростремительного ускорения:
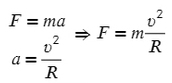
Для нахождение скорости спутника около поверхности планеты применяется формула:
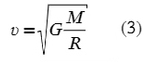
А вот для скорости на расстоянии «H» от Земли, формула будет такой:

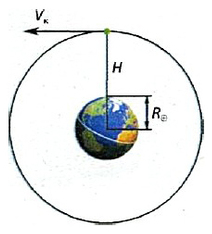
С помощью этой же формулы можно найти и первую космическую скорость — это минимальная скорость, которую необходимо придать телу, чтобы он совершал движение по круговой орбите вокруг планеты и не упал обратно на планету (это как с ведром воды, если раскрутить его до большой скорости, вода выливаться не будет и начнет оказывать все большее давление на дно ведра).
Проще говоря, для выхода на околоземную орбиту (160-2000 км от поверхности) требуется достичь данной скорости, иначе Земля притянет тело обратно. Первая космическая скорость для орбиты, расположенной вблизи поверхности Земли, составляет чуть меньше 8 км/с.
А для упрощения первую космическую скорость можно из формулы (2) и (3) :
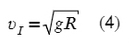
Если есть первая космическая, значит, есть и другие? Конечно есть:
υ₂ — минимальная скорость, которую нужно развить, чтобы начать отдаляться от Земли (11,2 км/с).
υ₃ — скорость «ухода» из Солнечной системы. Самая большая сила потребуется, чтобы «оторваться» от притяжения Солнца. Точного значения здесь нет, т.к. все зависит от того, в каком направлении будет двигаться спутник. Диапазон скоростей без учета влияния других планет солнечной системы составляет от 16,6 км/с до 72,8 км/с.
υ₄ — скорость «ухода» из Галактики. Еще больше неизвестных факторов для определения этой скорости. Но точно потребуется не меньше 220 км/с! Полет от Москвы до Лос-Анджелеса за 44 секунды?
С помощью формул (1), (2), (3) можно решить почти все задачи на данную тему.

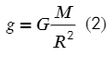
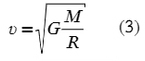
Да – да, рекомендую их выучить, на худой конец записать!
Задача №1. C какой силой притягиваются два корабля массой 50000 т на расстоянии 100 м от центров друг друга?
Закон всемирного тяготения действует на любые тела, но его сила зависит от массы тел, поэтому, чем больше массы, тем больше сила!

Массы двух кораблей знаем (нужно перевести в кг), расстояние между их центрами знаем, остается подставить и посчитать:
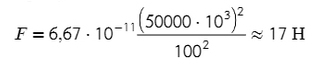
Ответ: 17 Н.
Задача №2. Ускорение свободного падения на поверхности Юпитера 24,9 м/с², а радиус планеты 7,13×10⁷ м. Вычислите среднюю плотность планеты.
Зная ускорение свободного падения и радиус, можно найти массу планеты:

Напомню, что плотность находится делением массы на объем.
А как же найти объем? Форму планеты можно принять за шар, а объем шара:
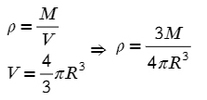
Подставив значения, получим, что плотность Юпитера чуть больше плотности воды, это и не удивительно, она же газовый гигант:

Ответ: 1250 кг/м³.
Задача №3. На каком расстоянии от центра Земли период обращения искусственного спутника будет равен 24 часам, так что спутник сможет занимать относительно вращающейся Земли неизменное положение (период обращения Земли равен периоду обращения спутника, называется такой спутник геостационарный).
Составители задачек считают незнание массы Земли плохим тоном. Но мне несложно напомнить: M = 6×10²⁴ кг.
Ух, ну и задачка! Какой-то период дан, которого ни в какой формуле нет.
В этой задаче для упрощения вывода формул зададим расстояние от центра до спутнка, как R.

Не сомневаюсь, что ты знаешь, что время в равномерном движении — это путь, деленный на скорость.
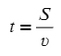
А если мы движемся по окружности, то время, за которое пройдем целый круг, можно назвать периодом, а путь — длиной окружности.
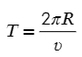
Чтобы спутник находился на одном расстоянии от центра Земли, воспользуемся формулой (3):

Дело за малым: подставить в формулу периода формулу скорости.

Осталось выразить радиус и подставить числа:
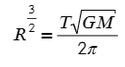
Еще один скользкий момент: T = 24 ч = 1440 м = 86400 с.

Ответ: 42 тыс. км.
Задача №4 (c ЕГЭ). Известно, что один оборот вокруг своей оси Венера совершает примерно за 243 земных суток, а масса Венеры составляет 0,82 от массы Земли. На орбиту какого радиуса надо вывести спутник Венеры, чтобы он всё время «висел» над одной и той же точкой поверхности? Известно, что спутники Земли, «висящие» над одной и той же точкой поверхности, летают по орбите радиусом R = 42000 км.
Данная задачка чем-то напоминает предыдущую. Честно говоря, это почти та же самая задача. Только тут спрашивается про спутник Венеры
Начать предлагаю с доказательства, что геостационарная орбита Земли находится на расстоянии 42000 км:

Нас не обманули! Получается, что геостационарный спутник имеет период обращения 1 сутки, как и Земля.
Что же касается Венеры, то тут период должен составлять 243 суток = 20995200 секунд.
А масса Венеры 0,82×6×10²⁴ кг.
Подставляем в ту же формулу, что и в предыдущей задаче:

Ответ: 1530 тыс. км.
Задача №5. Средняя плотность планеты Плюк равна средней плотности планеты Земля, а радиус Плюка в два раза больше радиуса Земли. Во сколько раз первая космическая скорость для Плюка больше, чем для Земли?
Для начала разберемся, как же отличаются массы. Для этого представим массу Плюка и Земли через плотность и объем Земли:

Скорость можно найти по любой из этих двух формул:

Проще всего воспользоваться первой, зная, во сколько раз отличаются массы и радиусы, получим ответ.

Ответ: 2
Сложность этой темы в большей степени заключается в рассчетах: числа большие, степени сложные. А вот обилием формул эта тема не похвастается, все основные представлены в начале.
Так же не забывай проверять себя «на глупость»: масса планеты, скорее всего, не может быть 1000 т, а космическая скорость — 120 м/с.
Будь в курсе новых статеек, видео и легкого технического юмора.
![]()
Мед это тело или вещество ?
djjey [1]
Мед это вещество обращайся
0
0
2 года назад
![]()
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Какую работу совершила пуля
uporotyy-lis [1.1K]
По законам сохранения энергии получаемДж
0
0
2 года назад
![]()
[50 Б.] Электротехника.
Валя Янко
Ответ:
Iф =Iл=9.84а
Объяснение:
Дано: Uл=220в
cos фи=0.8
Р=3квт/// Найти Iф, Iл – ?
Iф=Р/ √3* Uл*cos фи=3000/1.73*220*0.8=9.84а
0
0
1 год назад
![]()
Визначити магнітний момент кільцевого провідника радіусом 5 см,якщо по ньому проходить струм 12 А.
Самира Х
Магнитный момент:
M = I·S
Площадь:
S = π·R² = 3,14·(0,05)² ≈ 7,85·10⁻³ м²
Тогда:
M = 12·7,85·10⁻³ ≈ 0,094 А·м²
0
0
2 года назад
![]()
Давление жидкости на дно сосуда зависит только от…?
Владимир Пальшин
Зависит от плотности жидкости и высоты столба сосуда .
0
0
2 года назад
