Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем 
, умноженный на плотность его материала 
(см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой 
обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: 
, где 
— длина, 
— ширина, 
— высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: 
, где 
— диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: 
, где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: 
, где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: 
, где 
— площадь основания, — высота конуса.
Для круглого конуса: 
, где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями 
и 
: 
, где 
, 
. После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: 
, где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями 
и 
: 
, где 
, 
.
Исчеркав половину тетрадного листа, получаем: 
, где 
, 
— ширина и длина большего основания, 
, 
— ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: 
.
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (
, 
) формула выглядит проще:
2018-10-20 
Полая прямая призма, сделанная из тонкого прочного листового материала, имеет высоту $L$, а ее основания представляют собой равнобедренные треугольники с углом $2 alpha$ между боковыми сторонами. У призмы аккуратно удалили боковую грань, лежащую напротив угла $2 alpha$, и поставили призму на гладкий стол так, что упомянутый угол оказался сверху (основание призмы лежит в плоскости рисунка, ее высота перпендикулярна плоскости рисунка). Вблизи оказавшегося сверху угла проделали маленькое отверстие, и начали медленно заливать через него внутрь призмы воду плотностью $rho$. В момент, когда уровень воды в призме достиг высоты $h$, вода начала вытекать из-под призмы. Найдите массу $m$ призмы с удаленной гранью, считая, что давление $P_{0}$ воздуха над водой в призме и снаружи одинаково и равно атмосферному.
Решение:
Силу тяжести, действующую на сосуд, должна уравновешивать сила давления на стенки сосуда со стороны воды. Найдём модуль силы давления $Delta F$, действующей на часть одной из стенок сосуда малой высотой $Delta x$, находящуюся на глубине $x$ (см. рис.):
$Delta F = frac{ rho gx L Delta x }{ cos alpha}$,
Проекция этой силы на вертикальную ось X равна
$Delta F_{x} = – rho gxL Delta x tg alpha$.
Чтобы найти проекцию $F_{x}$ полной силы, действующей на стенку, нужно просуммировать проекции сил, действующих на все участки, лежащие на глубинах от 0 до $h$. Это всё равно, что найти площадь под графиком зависимости $Delta F_{x}/ Delta x$ от $x$. Поскольку этот график линейный с угловым коэффициентом $rho g L tg alpha$, то
$F_{x} = – rho gL tg alpha frac{h^{2} }{2}$.
Осталось учесть, что у сосуда есть две стенки, и приравнять нулю сумму силы тяжести $m_{min}g$ и проекции силы давления $F_{x}$:
$m_{min}g + 2F_{x} = 0$, откуда $m_{min} = rho Lh^{2} tg alpha$.
Призма — многогранное тело, основаниями которого являются два равных многоугольника, лежащие в параллельных плоскостях. Остальными гранями являются параллелограммы.
Такие параллелограммы в призме называются боковыми.
Онлайн-калькулятор объема призмы
Призмы разделяют на некоторые типы:
- Треугольная призма — у нее основания — треугольники;
- Четырехугольная призма — у нее основания — четырехугольники;
- Пентапризма — пятиугольная призма.
Деление, в общем, продолжается до бесконечности.
Виды призм
Прямая — у такой призмы боковые грани образуют с основаниями прямой угол.
Правильная — ее основанием является какой-либо правильный многоугольник.
Усеченной называется призма, у которой основания не параллельны друг другу.
Формула объема призмы
Объем прямой призмы находится так же, как и объем других многогранников — путем умножения площади основания на высоту.
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания призмы;
hh — высота призмы.
Разберем задачу на нахождение объема прямой призмы.
Найти объем призмы, если ее основанием является равнобедренный треугольник с равными сторонами по 5 см5text{ см} и основанием в 6 см6text{ см}. Высота призмы равна 10 см10text{ см}.
Решение
a=5a=5
b=6b=6
h=10h=10
Вычисляем площадь основания. Нужно провести высоту в данном равнобедренном треугольнике. Тогда, по теореме Пифагора, получаем:
a2=l2+(b2)2a^2=l^2+Big(frac{b}{2}Big)^2,
где ll — высота равнобедренного треугольника.
Отсюда:
l2=a2−(b2)2l^2=a^2-Big(frac{b}{2}Big)^2
l=a2−(b2)2l=sqrt{a^2-Big(frac{b}{2}Big)^2}
l=25−9l=sqrt{25-9}
l=4l=4
Площадь равнобедренного треугольника SS это половина от произведения его основания на высоту:
S=12⋅b⋅l=12⋅6⋅4=12S=frac{1}{2}cdot bcdot l=frac{1}{2}cdot 6cdot 4=12
В нашем случае этот треугольник является основанием призмы, поэтому:
S=SоснS=S_{text{осн}}
Тогда объем призмы найдется по формуле:
V=Sосн⋅h=12⋅10=120 см3V=S_{text{осн}}cdot h=12cdot 10=120text{ см}^3
Ответ
120 см3.120text{ см}^3.
На нашем сайте вы можете оформить решение задач на заказ по самым низким ценам!
Тест по теме «Объем призмы»
Метод измерений и расчетные формулы
В
работе определяется плотность материала
призмы и прямого цилиндра.
Плотность
однородных тел
определяется формулой:
,
(1)
где
m – масса тела, V
– объем тела.
Объем
прямой правильной шестиугольной призмы:
,
(2)
где
d
-диаметр окружности, описанной вокруг
основания призмы, h – высота призмы.
Объем
прямого кругового цилиндра:
,
(3)
где
d – диаметр основания цилиндра, h – высота
цилиндра.
В
итоге, плотность материалов призмы и
прямого цилиндра определяется
соотношениями:
,
(4)
.
(5)
Измерения
высоты и диаметров проводятся
штангенциркулем и микрометром.
Порядок выполнения работы а) Подготовительная часть
1.
Получить шестиугольную призму, прямой
круговой цилиндр и измерительные
инструменты.
2.
Ознакомиться с конструкциями и принципами
действия штангенциркуля, микрометра,
весов.
3.
Проверить положение нуля на измерительных
инструментах.
4.
Зафиксировать приборные погрешности
штангенциркуля, микрометра, весов.
Б) Измерение плотности материала призмы
5.
Измерить 6 раз высоту призмы
вдоль различных ребер и занести результаты
измерений таблицу 1.
Таблица
1
-
№
hi,
мм1
2
3
4
5
6
Проверить,
не содержится ли в результатах измерений
грубых погрешностей (промахов); при
наличии промахов исключить их из
дальнейшей обработки.
6.
Рассчитать результат измерения высоты
призмы как среднее значение отдельных
наблюдений:
,
(6)
где
n
– число наблюдений.
7.
Рассчитать оценку среднеквадратического
отклонения наблюдений
высоты призмы по формуле:
.
(7)
8.
Рассчитать случайную погрешность
результата измерений
по формуле:
,
(8)
где
–
коэффициент Стьюдента для доверительной
вероятности
для n
наблюдений.
9.
Определить систематическую погрешность
измерений высоты. Считать её равной
приборной погрешности и рассчитать по
формуле:
,
(9)
где
дел
– цена деления измерительного инструмента.
10.
Найти результирующую погрешность
измерений высоты по формуле:
.
(10)
11. Измерить
6 раз диаметр окружности, описанной
вокруг основания прямой правильной
шестиугольной призмы, и занести результаты
измерений в таблицу 2.
Таблица
2
-
№
di,
мм1
2
3
4
5
6
Для
измеренных значений
провести вычисления, аналогично
предыдущему – по пунктам 6 – 10.
12.
Измерить 6 раз массу призмы и занести
результаты измерений в таблицу 3.
Провести вычисления в соответствии с
пунктами 6 – 10.
Таблица
3
-
№
mi,
мм1
2
3
4
5
6
13.
Используя найденные средние значения
высоты, диаметра и массы п, рассчитать
среднее значение плотности материала
призмы по формуле (4).
14.
Рассчитать абсолютную результирующую
погрешность измерения плотности призмы
как погрешность косвенного измерения
. Для этого использовать формулу:
,
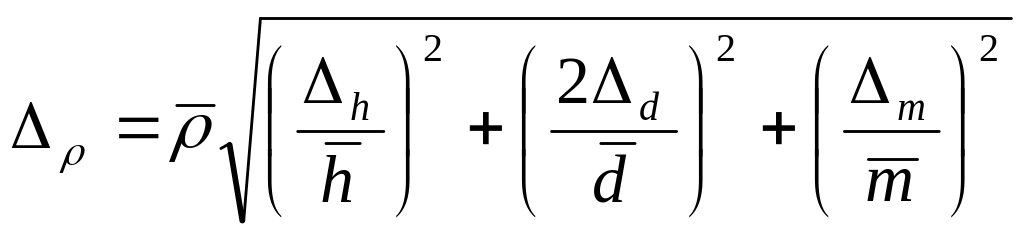
(11)
где
– результирующие погрешности измерений
высоты, диаметра описанной окружности
и массы призмы, соответственно.
Формула
(11) получена на основании расчетного
соотношения (4). А, именно: если
прологарифмировать (4), а затем
продифференцировать полученное
соотношение и заменить дифференциалы
на конечные разности, то, в итоге:
/
= m/m
– 2d/d
– h/h. (12)
Соотношение
(12) выражает относительную погрешность
значения плотности через относительные
погрешности значения массы, диаметра
и высоты. Так как знак слагаемых в правой
части равенства (12) может быть и
положительным и отрицательным, то в
наименее благоприятном случае все
значения относительных погрешностей
в правой части равенства должны
суммироваться:
/
= m/m
+ 2d/d
+ h/h. (13)
Однако,
наиболее вероятен случай, когда знаки
некоторых слагаемых противоположны
и они частично компенсируют друг друга.
Поэтому, в теории погрешностей установлена
рекомендация: вместо суммирования
модулей погрешностей находить корень
квадратный из суммы их квадратов.
Таким
образом, вместо формулы (13), для вычисления
результирующей погрешности измерения
плотности призмы следует использовать
формулу (11).
Подобный
подход к получению расчетной формулы
для результирующей погрешности измерения
плотности цилиндра базируется на формуле
(5), но он приводит к формуле, математически
идентичной формуле (11).
15.
Представить окончательный результат
измерений в виде:
,
кг/м3.
(13)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое призма
Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоскими гранями. Название зависит от фигуры, которая лежит в ее основании. Например, если это треугольник, призму называют «треугольной».
Эта объемная фигура может быть нескольких видов:
- Прямая. То есть с боковыми ребрами, перпендикулярными основанию.
- Правильная. В основании лежит правильный многоугольник.
- Наклонная. Ее ребра расположены под углом к основанию.
Формулы вычисления объема правильной призмы
Правильные призмы могут быть разных видов, в зависимости от многоугольника, который лежит в их основании. Формула вычисления объема во всех случаях выглядит одинаково:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(V=Scdot h)
Разница лишь в том, каким образом находится площадь S для каждой из фигур.
Треугольная
Чтобы вычислить объем призмы, в основании которой лежит правильный треугольник, используем формулу:
(V=frac{sqrt3}4cdot a^2cdot h)
Где (frac{sqrt3}4cdot a^2=S) — площадь правильного треугольника в основании, a — сторона треугольника, h — высота всей фигуры.
Четырехугольная
Для фигуры, в основании которой лежит квадрат, используем следующую формулу для вычисления объема:
(V=a^2cdot h)
Где a — сторона квадрата.
Пятиугольная
В этом случае объем будет вычисляться по формуле:
(V=frac52cdot acdotsqrt{left(frac a{2sinleft({displaystylefracpi5}right)}right)^2-frac{a^2}4}cdot h\)
Шестиугольная
Для призмы с правильным шестиугольником в основании формула объема выглядит так:
(x = V=frac{3sqrt3}2cdot a^2cdot h\)
Объем наклонной и прямой
Он находится через произведение площади основания на высоту:
(V=Scdot h\)
Таким образом, формула вычисления объема совпадает с предыдущими вариантами и зависит лишь от фигуры в основании.
С прямой призмой все то же самое. Сначала нужно вычислить площадь ее основания, а потом умножить на высоту.
Примеры задач
Задача № 1
Известно, что площадь основания призмы равна 12 (см^2), а длина ее высоты — 5 см. Вычислить объем фигуры.
Решение:
Так как уже дана площадь основания, нам не важно какая фигура лежит в основании. Подставляем известные значения в формулу:
(V=Scdot h=12cdot5=60 ) (см^3)
Ответ: V=60 (см^3.)
Задача № 2
В основании прямой призмы лежит четырехугольник со сторонами a и b по 6 см и 3 см. Высота данной фигуры равна 10 см. Рассчитать ее объем.
Решение:
Так как сначала для вычисления объема нам нужно определить площадь четырехугольника, будем использовать уравнение: (V=acdot bcdot h)
Подставляем значения: (V=6cdot3cdot10=180) (см^3)
Ответ: V=180 (см^3.)
