Пружинный маятник .
Пружинный маятник представляет из себя груз на пружине.
(T=2 pi sqrt{dfrac{m}{k}} )
(k) – жесткость пружины маятника
(m) – масса груза
Задача 1.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=8 Н/м ), а масса его груза
(m=0,5 кг ) ,
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=81 Н/м ), а масса его груза
(m=1 кг ) ,
(pi=3,14 )
Ответ округлить до десятых
Показать ответ
Показать решение
Видеорешение
Задача 3.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти массу груза пружинного маятника, если его период ( T=1 с )
, а коэффициент жесткости пружины ( k=400 Н/м ; )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 5.
Найти массу груза пружинного маятника, если его период ( T=0,3 с )
, а коэффициент жесткости пружины ( k=350 Н/м ; )
(pi=3,14 ).
Ответ округлить до десятых.
Показать ответ
Показать решение
Видеорешение
Задача 6.
Найти массу груза пружинного маятника, если его период ( T=0,07 с )
, а коэффициент жесткости пружины ( k=150 Н/м ; )
(pi=3,14 ).
Ответ округлить до сотых.
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,07 с )
, а масса груза ( m=0,0186 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 8.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,32 с )
, а масса груза ( m=0,8 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 9.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,6 с )
, а масса груза ( m=4 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 10.
Найти частоту колебаний ( nu ) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 15.
Массу груза пружинного маятника увеличили в 4 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 16.
Массу груза пружинного маятника увеличили в 25 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 25.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,4 с. ;; )
Масса его груза (m_1=1 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз массой (m_2=3 кг. ; )
Вычислить период колебаний пружинного маятника после присоединения дополнительного груза.
Показать ответ
Показать решение
Видеорешение
Задача 30.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,15 с. ;; )
Масса его груза (m_1= 0,6 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз , после чего
его период стал равен (T_2=0,45 с )
Найти массу (m_2 ) дополнительного груза.
Показать ответ
Показать решение
Видеорешение
Формулы пружинного маятника в физике
Формулы пружинного маятника
Определение и формулы пружинного маятника
Определение
Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
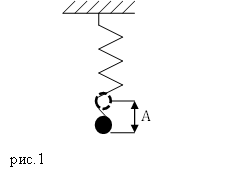
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${щu}^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
[T=2pi sqrt{frac{m}{k}}left(4right).]
Так как частота колебаний ($nu $) – величина обратная к периоду, то:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]
Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).
Амплитуду можно найти как:
[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]
начальная фаза при этом:
[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]
где $v_0$ – скорость груза при $t=0 c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
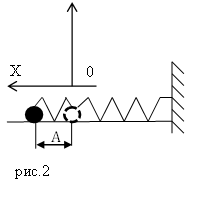
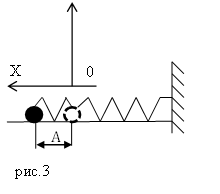
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
[E_p=-frac{dF}{dx}(8)]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]
Закон сохранения энергии для пружинного маятника запишем как:
[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]
где $dot{x}=v$ – скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ – кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
[E_{pmax}=E_{kmax }left(1.1right),]
где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ – кинетическая энергия шарика, в момент прохождения положения равновесия.
[E_{kmax }=frac{mv^2}{2}left(1.2right).]
Потенциальная энергия равна:
[E_{pmax}=frac{k{x_0}^2}{2}left(1.3right).]
В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:
[frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).]
Из (1.4) выразим искомую величину:
[x_0=vsqrt{frac{m}{k}}.]
Вычислим начальное (максимальное) смещение груза от положения равновесия:
[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).]
Ответ. $x_0=1,5$ мм
Пример 2
Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ – постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$.
В какой момент времени это произойдет?
Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:
[F=-kx=-kA{cos left(omega tright)left(2.1right). }]
Потенциальную энергию колебаний груза найдем как:
[E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.]
Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$
Читать дальше: формулы равноускоренного прямолинейного движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
vectra major
Ученик
(125),
на голосовании
14 лет назад
Голосование за лучший ответ
Снежный_барс
Мастер
(1987)
14 лет назад
m=k*T(квадрат) 4П (квадрат)
Похожие вопросы
Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками.
Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.
Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.
Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.
Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!
Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г
IV. Тест по русскому языку
1. В тексте про белых медведей больше всего предложений:
а) повествовательных; б) вопросительных
2. Восклицательное предложение находится:
а) в начале текста; б) в конце текста
3. Вопросительное предложение находится
а) в начале текста; б) в конце текста
4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются
а) родственными словами; б) однородными членами предложения
5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:
а) I спряжения; б) II спряжения
6. Эти глаголы стоят в форме:
а) настоящего времени; б) будущего времени; в) прошедшего времени
7. Эти глаголы стоят в форме:
а) единственного числа; б) множественного числа
8. Эти глаголы стоят в форме:
а) 1-го лица; б) 2-го лица; в) 3-го лица; г)нельзя определить лицо
9. Эти глаголы стоят в форме:
а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род
10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:
а) два слова; б) три слова
11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж:
а) Р.п.; б) В.п.