Определение массы радиоактивного препарата
Цель
работы:
познакомиться
с явлением радиоактивности, определить
массу радиоактивного препарата по его
активности.
Оборудование:
контейнер с препаратом, счетчик импульсов
радиоактивного излучения.
ТЕОРЕТИЧЕСКОЕ
ВВЕДЕНИЕ
Радиоактивностью
называется явление самопроизвольного
распада атомных ядер с превращением
одних ядер в другие, сопровождаемое
испусканием элементарных частиц. Распад
испытывают нестабильные ядра. Энергия,
выделяющаяся при распаде, очень велика
(несколько МэВ) и может быть определена
по соотношению Эйнштейна как произведение
разности масс покоя исходного ядра и
продуктов распада на квадрат скорости
света
![]() .
.
Существует
несколько видов радиоактивного распада.
При
альфа–распаде
из ядер вылетают α-частицы.
Они обладают двойным положительным
элементарным зарядом, а их масса
составляет 4 атомных единицы. То есть
это ядра гелия, состоящие из двух
протонов и двух нейтронов. Испытывают
α-распад
в основном ядра тяжелых элементов,
стоящих в таблице Менделеева за свинцом.
Образовавшиеся ядра также могут быть
радиоактивными, поэтому возникает
цепочка распадов, заканчивающаяся на
изотопах свинца и на висмуте. Существует
4 радиоактивных семейства с массовыми
числами 4n,
4n+1
4n+2
4n+3.
Если
материнское ядро X
испытывает
α-распад,
то оно
превращается
в дочернее ядро Y,
стоящее в таблице Менделеева на две
клеточки ближе к началу, с массовым
числом меньше на 4 единицы:
![]() .
.
(1)
Кинетическая
энергия α-частиц
принимает дискретные значения, что
свидетельствует о дискретности
энергетических уровней ядер.
Бета-распад
происходит при распаде ядер с вылетом
электрона или позитрона. Бывает, что
ядро захватывает один из ближайших
электронов с электронной оболочки и
испытывает β-превращение.
Кроме того, при электронном β-распаде
из ядра вылетает еще антинейтрино, а
при позитронном – нейтрино. Нейтрино
– это элементарная частица без
электрического заряда, масса покоя
которой, возможно, равна нулю. Уравнение,
например, электронного распада имеет
вид
![]() .
.
(2)
При
электронном бета-распаде дочернее ядро
смещается на одну клеточку к концу
таблицы Менделеева, при позитронном
распаде – на одну клеточку к началу
таблицы. Спектр энергии β-частиц
− сплошной,
так как некоторую, неопределенную часть
энергии уносят нейтрино.
Альфа-
и бета-распады сопровождаются
гамма-излучением. Это жесткое,
коротковолновое электромагнитное
излучение с огромной энергией до
нескольких МэВ, с большой проникающей
способностью. Оно обусловлено излучением
дочернего ядра, которое после распада
оказалось в возбужденном состоянии,
при переходе его в основное состояние.
Получим
уравнение закона радиоактивного распада.
Распад
ядра – это явление случайное, независимое
от других ядер, от внешних воздействий
(нагрев, электрические поля). Поэтому,
согласно теории вероятности, число
распавшихся за небольшой промежуток
времени ядер пропорционально времени
наблюдения и числу радиоактивных ядер:
![]() .
.
(1)
Здесь
λ –
постоянная распада, имеющая определенное
значение для каждого радиоактивного
изотопа. Она равна величине, обратной
среднему времени жизни радиоактивного
ядра. Знак минус показывает, что число
нераспавшихся ядер N
уменьшается.
Чтобы
определить закон уменьшения числа ядер
за достаточно большое время, проинтегрируем
уравнение (1) по времени от нуля до
некоторого момента t:
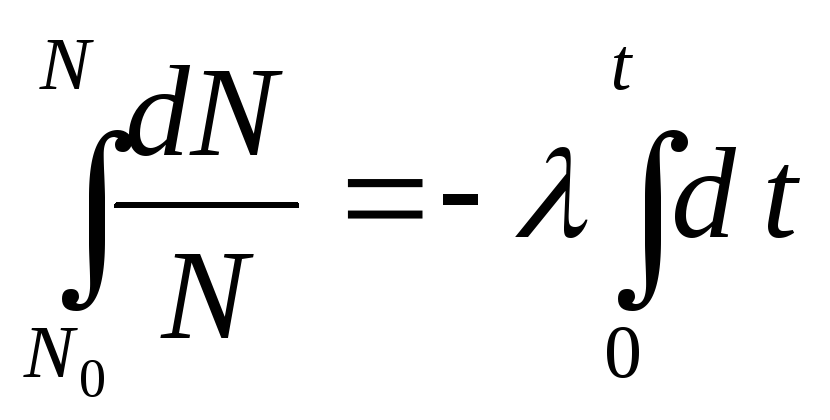 .В результате
.В результате
получим, что число нераспавшихся ядер
уменьшается со временем наблюдения от
начального числа N0
по экспоненциальному закону (рис. 1):
![]() .
.
(2)
В ремя,
ремя,
в течение которого распадается половина
исходного числа ядер, называется периодом
полураспада. По этому условию![]() .
.
Откуда получим соотношение![]() .
.
Период полураспада известных ядер
находится в пределах от 10–7секунды
до 1015
лет. Чем меньше период полураспада, тем
выше активность препарата.
Активностью
называется число распадов в единицу
времени. Из уравнения (1)
![]() .
.
Единицей активности является беккерель
(Бк), равный одному распаду в секунду.
По
известной активности можно определить
число радиоактивных ядер и, значит,
массу препарата. Число ядер в определенной
массе вещества можно установить по
закону Авагадро, согласно которому в
одном моле любого вещества содержится
одинаковое число атомов, равное NA
= 6,02 ∙1023
1/моль. Тогда
![]() ,
,
гдеM
– масса одного моля вещества. Подставив
N
в формулу
активности, получим формулу для расчета
массы препарата:
![]() .
.
(3)
Исследуемый
радиоактивный препарат плутония Pu239
небольшой массы находится в свинцовом
контейнере установки. Измерение
активности производится с помощью
счетчика Гейгера, подключенного к
пересчетному прибору (рис. 2).
Счетчик
Гейгера представляет собой тонкостенную
металлическую трубку, наполненную газом
при низком давлении. Трубка является
катодом, а анодом служит тонкая нить,
натянутая по оси трубки. Между ними
приложено напряжение 400–1000 В. При
пролете внутри трубки γ-фотона,
α-, β-частиц,
вследствие ионизации молекул газа,
возникают электроны и положительные
ионы.
Э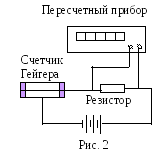 лектроны,
лектроны,
ускоряясь в сильном электрическом поле
около нити, производят вторичную
ионизацию молекул. В результате в
счетчике возникает лавинный разряд.
Чтобы зарегистрировать следующуючастицу,
разряд следует погасить. Для гашения
разряда последовательно со счетчиком
включается резистор с большим
сопротивлением. В момент разряда на
резисторе возникает импульс напряжения,
который регистрируется.
Однако
не каждая частица, пролетающая через
счетчик Гейгера, вызывает лавинный
разряд, а только малая доля, менее
процента. Это учитывается коэффициентом,
который называется эффективностью
счетчика ε.
Кроме того, радиоактивное излучение
изотропно, распространяется в полном
телесном угле 4π
стерадиан,
а на счетчик Гейгера попадает только
часть излучения, равная отношению
видимой площади счетчика S
к площади
сферы с радиусом, равным расстоянию от
препарата до счетчика:
![]() .
.
Это так называемая геометрическая
поправка. Таким образом, скорость счета
импульсов в установке меньше активности
препарата:![]() .
.
С учетом поправок формула (3) примет вид
![]() .
.
(4)
Здесь
n
– число
импульсов, зарегистрированных за время
счета t,
С –
постоянная
установки.
ВЫПОЛНЕНИЕ
РАБОТЫ
1. Включить
пересчетный прибор в сеть 220 В. На
индикаторе должно установиться время
10 с. Кнопками «+» и «–» установить
время счета импульсов не менее 300 с.
2. Нажать
кнопку «Установка». Нажать кнопки
«Сброс» и «Пуск», начнется счет времени
и числа импульсов. Через
установленное
время счет
остановится.
Повторить
измерения не менее трех раз. Записать
в табл. 1 число зарегистрированных
импульсов n
в каждом
опыте.
3. Произвести
измерения интенсивности фона космического
излучения в течение 300 с. Так как
контейнер с установки убирать нежелательно,
то следует поставить свинцовую пластину
в нишу контейнера для отсечения излучения
источника. Записать результат в табл. 2.
Выключить
установку.
Таблица 1
|
Число |
4. Произвести
расчеты. Определить среднее значение
числа зарегистрированных импульсов
<n>
. Определить число регистрируемых
импульсов с вычетом фона. Определить
скорость счета импульсов
![]() .
.
Рассчитать постоянную установки![]() при следующих значениях величин:М
при следующих значениях величин:М
= 239 г/моль,
NA
= 6,02∙1023
1/моль,![]() Т
Т
= 2,44∙104
лет или Т =
7,69∙1011
с, ε
= 1,2∙10–2,
р =1,3∙10–2.
Записать в табл. 2.
Таблица 2
|
Фон |
|
|
Среднее |
|
|
Число |
|
|
Постоянная |
|
|
Масса |
5. Определить
среднее значение массы препарата по
скорости счета по формуле
![]() .
.
6. Оценить
случайную погрешность измерений по
формуле
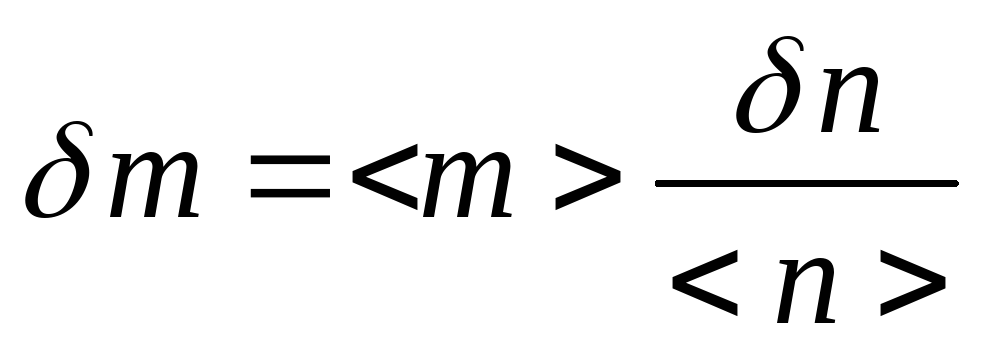 ,
,
где случайная погрешность прямых
измерений числа импульсов равна
![]() .
.
(5)
Здесь
k
– число
опытов.
7. Записать
результат m
=<m>±δm,
Р= …
Сделать выводы.
КОНТРОЛЬНЫЕ
ВОПРОСЫ
1. Дайте
определение альфа–распада.
Что представляют собой
α-частицы?
Запишите уравнение распада.
2. Дайте
определение бета-распада. Что представляют
собой β-частицы?
Запишите уравнение электронного или
позитронного распада. Почему спектр
энергии β-частиц
сплошной?
3. Дайте
определение гамма-излучения.
4. Выведите
уравнение закона радиоактивного распада.
Дайте определение периода полураспада,
активности препарата.
5. Объясните
принцип работы счетчика Гейгера,
назначение резистора в схеме включения
счетчика. Дайте определение эффективности
счетчика.
6. Выведите
формулу для расчета массы радиоактивного
препарат по измеренной скорости счета
импульсов счетчика Гейгера. Объясните
смысл геометрической поправки.
Работа 47
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача. Определите массу не распавшегося радиоактивного вещества по истечении суток, если вначале его масса была
кг. Период полураспада вещества
дней.
Решение
Думаем: в задаче рассматривается радиоактивный распад. И единственное, что мы можем о нм сказать, это закон радиоактивного распада.
(1)
- где
Однако, нам задано и необходимо проанализировать не количество элементов, а массу вещества. Связь между ними через химическое количество вещества:
(2)
Решаем: работа с уравнениями вида (1) имеет свою логику. Мы можем домножить правую и левую части уравнения на одну и ту же совокупность переменных. Исходя из (2) домножим на . Получим:
(3)
Считаем: перевод в систему СИ необходим, однако в степени соотношения (3) главное, чтобы время и период полураспада совпадали по размерности. Пусть все параметры будут в днях. Тогда:
(кг)
Ответ: (кг)
Ещё задачи по теме «Закон радиоактивного распада»
Как правильно решать задачи на закон радиоактивного распада
Реакции первого порядка
Задача 67.
При лечении онкологических заболеваний в организм пациента вводят препарат, содержащий радиоактивный изотоп. Считая радиоактивный распад реакцией первого порядка, определить какая часть радионуклида останется в организме больного через 30 суток, если период полураспада составляет 130 суток.
Решение:
По истечении периода полураспада масса радиоактивного материала уменьшается в два раза. Поэтому количество периодов полураспада вещества будет равно n = (30/130). Поэтому, после n периодов полураспада через 30 суток в организме останется следующая часть радионуклида:
(1/2)n = (1/2)(30/130) = (1/2)0,231 = 0,852 или 85,2%.
Ответ: останется 85,2% радионуклида.
Задача 66.
Найти массу радиоактивного материала через промежуток времени, равный четырем периодам полураспада. Начальная масса материала составляла 60 г.
Решение:
По истечении периода полураспада масса радиоактивного материала уменьшается в два раза. Поэтому, после четырех периодов полураспада масса материала будет составлять:
(1/2)4 = 1/16
от первоначального количества. Следовательно, через заданный промежуток времени масса вещества будет равна:
m(конечн.) = (1/16 . m(нач.) = 1/16 . 60 = 3,75 г.
Ответ: m(конечн.) = 3,75 г.
Задача 68.
Период полураспада некоторого вещества 3 недели. Через какое время количество нераспавшихся ядер уменьшится в 16 раз.
Дано:
T = 2 недели;
N = 1/16 . N0;
t = ?
Решение:
Так как N = N0 . 2(-t/2);
(1/16 . N0) = N0 . 2(-t/2);
1/2(4) = 2(-t/2);
-4 = -t/2;
t = (-4) . (-2) = 8 недель.
Ответ: t = 8 недель.
Задача 69.
Какая доля от большого количества радиоактивных ядер остаётся нераспавшейся через интервал времени, равный пяти периодам полураспада?
Решение:
Для расчета нераспавшейся доли радиоактивных ядер используем уравнение: N = N0 . 2(-t/Т), где
N0 – количество радиоактивных ядер в произвольно выбранный начальный момент времени t = 0, N – количество радиоактивных ядер, не распавшихся к моменту времени t, Т – период полураспада.
Учитывая, что t = 4T получим:
N = N0 . 2(-4t/Т);
N = N0 . 2(-4) = 100% . 1/23 = 100% .1/16 = 6,25%.
Ответ: 6,25%.


Разбор задач из учебника 11 класса
Авторы
Жилко В. В., Маркович Л. Г.
Издательство
Народная асвета
Отличный помощник для учеников 11 класса. Главная задача данного сайта: помочь добросовестным ученикам понять ход решения и научиться решать аналогичного рода задачи на занятиях и дома. Все задачи разобраны исключительно в образовательных целях. Автор данного сайта категорически не приветствует списывание. По вопросу репетиторства обращаться по контактам, которые можете найти в разделе “О себе”.
Краткое условие задачи №3
Определите массу m нераспавшегося радиоактивного вещества по истечении суток, если вначале его масса была m0 = 1,0 кг. Период полураспада вещества T1/2 = 10 дней.

Решение задач предоставлено исключительно в образовательных целях. Все решения защищены авторским правом и принадлежат лидеру данного сайта. Любое копирование данных с данного ресурса без согласия автора — это нарушение закона об авторском праве и смежных правах, которое
ведет к административной и уголовной ответственности
Лучше чем решеба в миллион раз!
Самый крутой ГДЗ по физике. Браво!
Лучший решебник по физике из существующих! В разы лучше чем resheba.top
Моя дочь занималась физикой в период с сентября по май, целью было повысить уровень знаний. Преподаватель пунктуальный и ответственный, хорошо и понятно объясняет, всегда есть наглядный материал для демонстрации лабораторых работ. Помог разобраться с решением задач. Обучение проходило онлайн. Ребенок остался доволен – повысились знания и успеваемость. Рекомендую
Квалифицированный педагог, легко нашел общий язык с подростком. Обьясняет доступно. Сыну нравится заниматься. Оценки стали лучше.
Очень понравился. Сильный преподаватель, быстро нашёл подход к ребёнку, доступно объяснял материал.За год подготовил нас к сдаче ЦТ по физике. Спасибо огромное. Мы рады,что вы с нами работали.
Плюсы: Тактичный, обязательный, современный преподаватель, который может найти подход к ребенку, общается с ним на равных и может вызвать интерес к предмету
Минусы: Не заметили
Описание: О работе репетитора в первую очередь можно судить по успехам ребенка. Мой ребенок стала чувствовать себя в разы увереннее в решении задач по физике и в целом очень повысилось понимание предмета
Дмитрий замечательный специалист. Очень ответственно относится к проведению занятий, даёт много материала в доступной форме. Быстро нашел общий язык с ребенком. Благодаря занятиям с Дмитрием, сын не только повысил свой уровень знаний и школьные отметки, но и физика стала одним из любимых предметов.Очень рекомендую занятия с данным специалистом.
Я сама по образованию педагог, и хочу отметить, что Дмитрий проявил себя как очень ответственный, конструктивно настроенный, эмпатийный профессионал своего дела, который умеет заинтересовать своим предметом и привить интерес. Благодаря занятиям с ним моя дочь выбрала для себя направление профиля “физ.-мат.” в старшей школе. Спасибо!
Плюсы: Пунктуальность, доступная и современная подача материала
Минусы: Нет
Описание: У подростка улучшилась успеваемость по физике, занятиями очень доволен. Однозначно рекомендую!
Выражаю благодарность Дмитрию за его работу. Очень ответственный человек и грамотный преподаватель. Его занятия в онлайн формате организованы и проходят на высоком уровне.
Занятия на 10+, у ребёнка проснулся интерес к физике, школьный балл с 6 поднялся до 9 за одну четверть.
Репетитор понравился. Проводил занятия с подростком и сумел привить интерес к предмету. Материал воспринимается легко, имеются конспекты с основными формулами по всем темам. Много наглядных материалов для лучшего понимания темы. Довольны результатами! Рекомендуем!
Хороший репетитор, доступно изгалагает материал, всегда пунктуален во времени проведения занятий, ребёнку нравиться с ним заниматься и есть результат в повышении уровня знаний. Мы довольны выбором данного репетитора. Рекомендуем.
Самый качественный сайт о физике!
Спасибо вам за качественную работу! Все четко. Отдельно респект за простую навигацию по сайту.
Лучший решебник по физике из существующих! В разы лучше чем resheba.top
решеба физика
физика решебник
решебник по физике
решебник физика
физика гдз
гдз физика
физика
сайт решений задач по физике
решить физику онлайн бесплатно
решить физику онлайн
физика задачи
по физике
учебные материалы по физике
учебники физики
решеба по физике
resheba top
megaresheba
Superresheba
ГДЗ путин
ГДЗ
формулы физика цт
все формулы по физике для цт
формулы по физике для цт
формулы для цт по физике
основные формулы физики
физика формулы
формулы из физики
физика основные формулы
все формулы по физике 7-11 класс
формулы по физике 7-11 класс
формулы по физике с 7 по 11 класс
все формулы по физике 7-11 класс скачать бесплатно
формулы по физике скачать
все формулы по физике скачать
физика основные понятия
дрт 2022 физика
репетиционное тестирование по физике 2014
физика тесты
физика цт задания
физик формулы
формулы по физике
потиху готовлюсь к цт, сайт очень помогает!
Огромное спасибо за Ваш труд. Очень нужное и полезное подспорье, когда закончил школу более 25 лет тому назад.
физику с вашим сайтом
теперь щелкаю как орешки))))
Есть вопросы?
Готовы ответить=)



Полезное

Механика. Кинематика и динамика
Методы физических исследований

Механика. Кинематика и динамика
Измерение расстояний и времени

Механика. Кинематика и динамика
Кинематика прямолинейного движения

Механика. Кинематика и динамика
Относительность движения

Механика. Кинематика и динамика
Первый закон Ньютона

Механика. Кинематика и динамика
Второй закон Ньютона

Механика. Кинематика и динамика
Третий закон Ньютона

Механика. Кинематика и динамика
Упругие деформации. Вес и невесомость

Механика. Кинематика и динамика
Сила всемирного тяготения

Механика. Кинематика и динамика
Сила трения

Механика. Кинематика и динамика
Исскуственные спутники Земли

Механика. Кинематика и динамика
Динамика вращательного движения

Законы сохранения в механике. Механические колебания и волны
Статика

Законы сохранения в механике. Механические колебания и волны
Закон сохранения импульса

Законы сохранения в механике. Механические колебания и волны
Закон сохранения момента импульса

Законы сохранения в механике. Механические колебания и волны
Закон сохранения эннергии в механике

Законы сохранения в механике. Механические колебания и волны
Закон Бернулли

Законы сохранения в механике. Механические колебания и волны
Механические колебания

Законы сохранения в механике. Механические колебания и волны
Механические волны

Законы сохранения в механике. Механические колебания и волны
Звуковые волны

Электромагнитные колебания и волны
Электромагнитные колебания

Электромагнитные колебания и волны
Переменный ток

Электромагнитные колебания и волны
Закон Ома для цепи переменного тока

Электромагнитные колебания и волны
Электромагнитные волны

Электромагнитные колебания и волны
Излучение электромагнитных волн

Электромагнитные колебания и волны
Радио и телевидение

Электростатика. Законы постоянного тока
Электрические заряды

Электростатика. Законы постоянного тока
Потенциал. Разность потенциалов

Электростатика. Законы постоянного тока
Диэлектрики в электрическом поле

Электростатика. Законы постоянного тока
Электроемкость

Электростатика. Законы постоянного тока
Постоянный электрический ток

Электростатика. Законы постоянного тока
Магнитное поле тока

Электростатика. Законы постоянного тока
Движение заряженнных частиц

Электростатика. Законы постоянного тока
Электромагнитная индукция

Электростатика. Законы постоянного тока
Магнетики

Электростатика. Законы постоянного тока
Электрические генераторы и двигатели

Электростатика. Законы постоянного тока
Трехфазная система токов

Электростатика. Законы постоянного тока
Электроизмерительные приборы

Электрический ток в различных средах
Электрический ток в металлах

Электрический ток в различных средах
Проводимость полупроводников

Электрический ток в различных средах
p-n переход

Электрический ток в различных средах
Транзистор

Электрический ток в различных средах
Электронно-лучевая трубка

Электрический ток в различных средах
Электрический ток в газах

Электрический ток в различных средах
Тлеющий разряд

Электрический ток в различных средах
Электрический ток в электролитах

Оптика и специальная теория относительности
Законы распространения света

Оптика и специальная теория относительности
Скорость света

Оптика и специальная теория относительности
Дисперсия света

Оптика и специальная теория относительности
Рентгеновское излучения

Оптика и специальная теория относительности
Применение электромагнитных волн

Оптика и специальная теория относительности
Интерференция света

Оптика и специальная теория относительности
Дифракция света

Оптика и специальная теория относительности
Линзы

Оптика и специальная теория относительности
Оптические приборы

Оптика и специальная теория относительности
Глаз

Оптика и специальная теория относительности
Эксперименнтальные основы СТО

Оптика и специальная теория относительности
Энергия и импульс в СТО

Оптика и специальная теория относительности
Законы сохранения в СТО

Оптика и специальная теория относительности
Масса и энергия частиц в СТО

Молекулярная физика
Дискретное строение вещества

Молекулярная физика
Взаимодействие частиц вещества

Молекулярная физика
Количество вещества

Молекулярная физика
Температура

Молекулярная физика
Давление газа

Молекулярная физика
Уравнение состояния идеального газа

Молекулярная физика
Теплоемкость

Молекулярная физика
Кристаллы

Молекулярная физика
Модели кристаллических решеток

Молекулярная физика
Ионный проектор

Термодинамика
Внутренняя энергия

Термодинамика
Работа газа

Термодинамика
Законы термодинамики

Термодинамика
Паровая машина Ползунова

Термодинамика
Паровая турбина

Термодинамика
Четырехактный двигатель внутреннего сгорания

Термодинамика
Газотурбинный двигатель

Термодинамика
Компрессионный холодильник

Термодинамика
Ракетные двигатели

Термодинамика
Энергетика и энергетические ресурсы

Квантовая физика
Открытие электрона

Квантовая физика
Фотоэффект

Квантовая физика
Спектры

Квантовая физика
Планнетарная модель атома

Квантовая физика
Модель атома водорода по Бору

Квантовая физика
Опыты Франка и Герца

Квантовая физика
Корпускулярно-волновой дуализм

Квантовая физика
Соотношение неопределенностей

Квантовая физика
Лазеры

Квантовая физика
Частицы и античастицы

Физика атомного ядра
Атомное ядро

Физика атомного ядра
Ядерные реакции

Физика атомного ядра
Радиоактивность

Физика атомного ядра
Свойства ионизирующих излучений

Физика атомного ядра
Методы регистрации частиц

Физика атомного ядра
Дозиметрия

Физика атомнного ядра
Допустимые и опасные дозы облучения

Физика атомного ядра
Ядерная энннергетика

Физика атомного ядра
Фундаментальные взаимодействия

Физика атомного ядра
Эволюция вселенной
В химии гравиметрия («весовой анализ») является арбитражным аналитическим методом. Какими бы ни были методы анализа, применяемые в настоящее время (сейчас получили распространение физико-химические и физические методы), все они так или иначе, применительно к задачам количественного анализа, сводятся к необходимости использовать некоторые исходные вещества в качестве эталонов. Последние могут быть изготовлены с использованием, в конечном итоге, аналитических весов.
Но в ядерной физике и радиохимии гравиметрический метод совершенно не распространен главным образом вследствие того, что в подавляющем числе радиоаналитических задач (и, тем более, в радиоэкологии) имеют дело с такими массами радиоактивных веществ, которые находятся за пределом чувствительности даже наилучших весов. Тем не менее помимо установления абсолютной активности радионуклидов, что выполняется инструментально, бывает необходимо знать и их массу (концентрацию). Это достигается элементарным расчетом на основе соотношения (1.10):
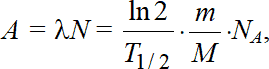
где m – масса радионуклида (г), M – молярная масса радионуклида (г/моль);
NA = 6,022045•1023 моль-1 – постоянная Авогадро.
Отсюда следует:
 . (1.17)
. (1.17)
(Здесь активность выражается в беккерелях, а период полураспада в секундах).
По этой формуле можно рассчитать массу, например, одного кюри любого радионуклида. Так, 1Kи 238 U (T1/2 = 4,5•109 лет) имеет массу около трех тонн, 1 Kи226Ra (T1/2= 1600 лет) – 1 г (это так и должно быть, т.к. один грамм именно этого изотопа радия в свое время был выбран за эталон одного кюри).
В то же время масса короткоживущих радионуклидов, имеющих T1/2 порядка нескольких лет или суток (не говоря уж о тех, период полураспада которых исчисляется секундами или долями секунды), в аналитическом смысле может оказаться настолько незначительной, эфемерной, почти нереальной, что ей нельзя будет приписать проявление каких бы то ни было макроскопических термодинамически фиксируемых свойств. Иными словами, химические (в общем случае термодинамические) характеристики любой фазы, в которую включается (или ею утрачивается, отдается) радиоактивный микрокомпонент, не могут измениться сколько-нибудь заметным образом, т.к. уровень концентрации этой примеси (выражаемый в процентах или в мольных долях) не более значим, чем уровень любых других практически неустранимых загрязнений, присутствующих даже в самых чистых химических препаратах.
Вот такие массы веществ и соответствующие им концентрации в радиохимической литературе получили название «невесомые количества», «микроколичества», или даже «ультрамикроколичества». А само вещество в таких количествах обычно называют микрокомпонентом.
С явлением радиоактивности (точнее – с экспоненциальным характером ее проявления) связан распространенный паралогизм – убежденность некоторых людей в том, что по истечении десяти периодов полураспада любой радионуклид практически распадается полностью.
Проанализируем справедливость этого утверждения. В соответствии с (1.11): N/N0 = 2 – n = 2–10 = 1/1024. При этом распалось (N0 – N) атомов:
Nрасп = N0 – N = N0 (1–1/1024).
Последнее выражение дает основание для высказывания двух суждений.
1) С одной стороны, 1–1/1024 ? 1, т.е. Nрасп ? N0, что соответствует итогу «радионуклид практически распался весь». Казалось бы, это утверждение в какой-то степени приемлемо, т.к. равенство Nрасп ? N0 выполняется с погрешностью (погрешность вычисления) менее 0,1%, о чем многие проектировщики могут только мечтать.
2) Но, с другой стороны, из того факта, что значение некоторой физической величины уменьшилось на три порядка, вовсе не вытекает следствие, что данную величину можно приравнять нулю. Это всего лишь «психологический софизм», поскольку здесь соединились два независимых сравнения, причем одно в процессе рассуждений подменяется другим.
В первом случае признается имеющим смысл фраза, что «0,00098 гораздо меньше (пренебрежимо меньше) единицы». Но и во втором случае оставшееся число атомов, N, тоже необходимо сравнить с каким-то другим эталоном, репером, нормой и т.п., но отнюдь не с единицей.
Скорей всего N и A, которые «остались» (Nост и Aост) после истечения 10 T1/2, нужно сравнивать с существующими нормами или потребностями. Если оценивается вредная сторона носителя радиоактивности, то сравнение должно происходить, например, с санитарными нормами (Aн). Здесь возможны различные ситуации:
Aн > Aост и даже Aн >> Aост, либо наоборот Aн<Aост, Aн << Aост (обычно в подобных сравнениях фигурируют удельные величины). Понятно, что житейские и юридические выводы, следующие отсюда, будут абсолютно различными. При этом совсем не исключено, что соотношение Aн << Aост может оставаться в силе не только по истечению 10 T1/2, но и после прошествия гораздо большего отрезка времени.
Таким образом, психологическому аспекту экспоненциальной зависимости редко отдают должное, она таит в себе ряд паралогизмов и не вписывается в интуицию человека. Эта зависимость наглядна только при сравнении ее с некоторым соответствующим пределом (нормой, репером, эталоном и т.п.).
У закона радиоактивного распада как у зависимости экспоненциального характера есть еще одна особенность, касающаяся временного поведения долгоживущих радионуклидов. В связи с этим рассмотрим один характерный пример.
Период полураспада урана-238 равен 4,5·109 лет. Какова убыль его активности вследствие распада за конкретный, но незначительный по сравнению с периодом полураспада интервал времени, например, за миллион лет?
Эта убыль, выражаемая в долях единицы, отнесенная к начальному значению активности, равна:

Положим t = 106 лет и преобразуем равенство следующим образом:

Обоснованно полагая ? величиной очень малой в сравнении с единицей, ограничимся первым линейным членом разложения логарифмической функции в ряд: ln(1 – ?) ? – ? . Тогда ? = (0,692•106/4,5·109) = 1,5 · 10–4 или 0,015%. Таким образом, активность урана-238 как функция времени может быть независимо рассмотрена в двух временных масштабах.
1) В геохронологическом масштабе времени (отрезки времени, сопоставимые, например, с возрастом Земли, признаваемым в космогонии) этот радионуклид значимо изменял свою активность. Так, если возраст Земли в настоящее время оценивается величиной порядка нескольких миллиардов лет, то с момента возникновения нашей планеты как тела Солнечной системы до наших дней активность содержащегося в геосфере урана-238 уменьшилась практически вдвое.
2) В технологическом (антропном) масштабе (отрезки времени, сопоставимые с интервалом, протекшим с момента возникновения Homo Sapiens, и гораздо меньшие), как только что было показано выше, активность этого радионуклида (и, естественно, всех других, обладающих такими же значительными периодами полураспада) может быть рассматриваема как практически независимая от времени:  . Это, разумеется, парадоксальный вывод, сбивший с толку даже Фредерика Содди, но он вполне объясним, если не забывать об иерархии масштабов времени, всегда принимаемой во внимание в естествознании.
. Это, разумеется, парадоксальный вывод, сбивший с толку даже Фредерика Содди, но он вполне объясним, если не забывать об иерархии масштабов времени, всегда принимаемой во внимание в естествознании.
Иными словами, обсуждение зависимости активности долгоживущих радионуклидов от времени имеет смысл и сопряжено с практически полезными расчетами только тогда, когда четко определен масштаб времени, в соответствии с которым это обсуждение проводится.
Данный текст является ознакомительным фрагментом.
