Масса ротора с учетом центробежной силы Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Теория машины ↺ | |
| Теория машины | Вибрации ↺ | |
| Вибрации | Продольные и поперечные колебания ↺ | |
| Продольные и поперечные колебания | Критическая или вращающаяся скорость вала ↺ |
|
✖Центробежная сила – это кажущаяся внешняя сила, действующая на массу при ее вращении.ⓘ Центробежная сила [Fc] |
+10% -10% |
||
|
✖Угловая скорость относится к тому, как быстро объект вращается или вращается относительно другой точки, т.е. как быстро изменяется угловое положение или ориентация объекта со временем.ⓘ Угловая скорость [ω] |
+10% -10% |
||
|
✖Начальное расстояние до центра тяжести ротора – это численное измерение расстояния между объектами или точками.ⓘ Начальное расстояние до центра тяжести ротора [e] |
+10% -10% |
||
|
✖Дополнительный прогиб ЦТ ротора – это степень смещения элемента конструкции под действием нагрузки.ⓘ Дополнительный прогиб ЦТ ротора [y] |
+10% -10% |
|
✖Масса ротора – это одновременно свойство физического тела и мера его сопротивления ускорению.ⓘ Масса ротора с учетом центробежной силы [m] |
⎘ копия |
Масса ротора с учетом центробежной силы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Центробежная сила: 35 Ньютон –> 35 Ньютон Конверсия не требуется
Угловая скорость: 14.2 Радиан в секунду –> 14.2 Радиан в секунду Конверсия не требуется
Начальное расстояние до центра тяжести ротора: 2 Миллиметр –> 0.002 метр (Проверьте преобразование здесь)
Дополнительный прогиб ЦТ ротора: 0.8 Миллиметр –> 0.0008 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
61.9916683197778 Килограмм –>61991.6683197778 грамм (Проверьте преобразование здесь)
12 Критическая или вращающаяся скорость вала Калькуляторы
Масса ротора с учетом центробежной силы формула
Масса ротора = Центробежная сила/((Угловая скорость^2)*(Начальное расстояние до центра тяжести ротора+Дополнительный прогиб ЦТ ротора))
m = Fc/((ω^2)*(e+y))
Что подразумевается под критической скоростью вала и какие факторы на нее влияют?
В механике твердого тела, в области динамики ротора, критическая скорость – это теоретическая угловая скорость, которая возбуждает собственную частоту вращающегося объекта, такого как вал, пропеллер, ходовой винт или шестерня. Фактором, влияющим на критическую скорость вала, является диаметр диска, размах вала и эксцентриситет.
Масса – ротор
Cтраница 1
Масса роторов и их конфигурация должны допускать пере-возку при помощи транспортных средств и волоком в пределах промысла. Роторы должны иметь устройства, позволяющие быстро обеспечивать фиксацию от вращения.
[1]
Масса ротора равна 18 кг, масса статора – 14 кг. Центр тяжести ротора мотора смещен по отношению к оси вращения на г 0 5 см, ротор вращается с угловой скоростью ш 24 рад / с.
[2]
Масса ротора насоса и осевое усилие на роторе воспринимаются пятой электродвигателя. Для уплотнения вала насоса используется мягкая сальниковая набивка.
[4]
Масса ротора электродвигателя вызывает две реакции: одна направлена вверх и действует на ближайшую к электродвигателю опору, другая направлена вниз и вследствие жесткости вала и значительных зазоров в коренных подшипниках может возникнуть не на второй, а на третьей, четвертой и частично даже на пятой опорах вала. При этом дополнительному изгибу подвергаются участки вала, отдаленные от электродвигателя.
[5]
Масса ротора двигателя значительно превышает по величине остальные вращающиеся массы привода, поэтому можно упростить расчетную схему, приняв ее двухмассовой односвязной. На рис. 87, а введены следующие обозначения: 11 – момент инерции ротора двигателя; I. Поведение данной системы рассматривается при учете внутренних сил неупругого сопротивления, пропорциональных скорости; г – коэффициент пропорциональности, равный величине демпфирующей силы при скорости, равной единице.
[7]
Масса ротора генератора 2 5 т, турбины – 1 1 т, частота вращения ротора 3000 об / мин.
[8]
Когда масса роторов сопоставима с массой подшипниковых опор или больше, абсолютные колебания валов могут достигнуть примерно таких же самых значений, как абсолютные колебания подшипников. В таких случаях рекомендуется измерять абсолютные колебания валов и корпусов подшипников.
[9]
Снижение массы ротора достигается за счет увеличения линейных нагрузок статора, плотности тока в обмотке ротора, выбора максимально допустимой индукции в зубцах ротора.
[10]
Уменьшение массы ротора и применение торсиона, размещенного в роторе, позволили уменьшить длину и массу двигателей на 10 – 15 %, а также существенно ( в 3 – 4 раза) увеличить стойкость узла соединения ротора с валом шпинделя. Кроме того, такая конструкция двигателя позволяет улучшить энергетическую характеристику двигателя, повысить его КПД и в 2 – 4 раза снизить уровень вибраций двигателя.
[12]
Центр масс ротора гироскопа О расположен па оси Oty. Оси Ox, Oy, Oz являются главными центральными осями – инерции ротора, его полярный и экваториальный моменты инерции равны С и А соответственно.
[13]
Определяют массу ротора и устанавливают резонансные-пружины станка и шейки ротора. Подбирают вкладыши и пришабривают их по шейкам ротора, обеспечив необходимые зазоры.
[15]
Страницы:
1
2
3
4
5
15.1
Масса изолированных проводов обмотки
статора:

15.2
Масса неизолированных проводов обмотки
фазного ротора:
 .
.
15.3
Масса стали сердечников статора и
ротора:

15.4
Масса изоляции статора:
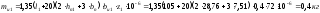
15.5
Масса изоляции фазного ротора:

15.6
Масса конструкционных материалов:

15.7
Масса двигателя:
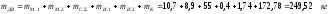
15.8
Динамический момент инерции:
 .
.
Заключение.

В
курсовом проекте произведен полный
расчет асинхронного двигателя с фазным
ротором номинальной мощностью 22 кВт и
номинальной частотой вращения 1000
об/мин
, питающийся от источника трехфазного
синусоидального напряжением 380/660 В
частотой 50 Гц. В результате получился
двигатель со следующими экономико-техническими
показателями:
КПД
– 89,8 %
Коэффициент
мощности – 0,882
Ток
статора – 24,13 А
Масса
двигателя – 249,52 кг
Величина
воздушного зазора – 0,5 мм
Активное
сопротивление обмотки статора – 0,375 Ом
Активное
сопротивление обмотки фазного ротора
– 0,00741Ом
Рассчитанному
двигателю соответствует стандартный
двигатель:
4АК200Б6УЗ
|
Типоразмер двигателя |
|
|
|
|
|
Ток ротора, А |
Напряжение ротора, |
Масса, кг |
|
4АК200Б6УЗ |
22 |
88 |
0,8 |
3,5 |
3,5 |
45 |
330 |
315 |
Список
использованных источников.
-
Гольдберг
О.Д., Гурин Я.С., Свириденко И.С.
Проектирование электрических машин
М: Высшая школа,2001. 430 с. -
Копылов
И.П.Электрические машины М: Энергоатомиздат,
1986. 360 с. -
Справочник
по электротехнике и электрооборудованию
под ред. И.И. Алиева. Ростов-на-Дону,
Феникс 2003г. – 469с. -
Справочник
по электрическим машинам / под
ред.И.Н.Копылова. М: Энергоатомиздат.
т.1.- 1988. – 456 с.

Соседние файлы в папке курсач docx51
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Высота паза определяется по следующей формуле:
(26)
Ширина паза:
(27)
(28)
где – высота шлица зуба, м;
– ширина шлица зуба, м.
Принимается =1 мм,
=4 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапециидального паза. Форма паза статора представлена в графической части проекта.
.
(29)
Для расчёта коэффициента заполнения паза необходимо определить площадь паза в свету и учесть площадь сечения паза, занимаемую корпусной изоляцией Sиз и прокладками в пазу Sпр. Размеры паза в свету определяются с учётом припусков на шихтовку и сборку сердечников bп и hп:
(30)
Из таблицы 8.12 [1, c. 292] bп=hп=0,3 мм.
Площадь поперечного сечения трапециидального паза, в которой размещаются обмотки, корпусная изоляция и прокладки:
. (31)
Площадь занимаемая корпусной изоляцией в пазу, м2:
(32)
где – односторонняя толщина изоляции в пазу, м.
Из таблицы 3.1 [1, c. 74] выбирается =0,55·10-3 м2, тогда:
Площадь поперечного сечения прокладок по 8.47, м2:
(м2 ) (33)
Площадь поперечного сечения паза, остающаяся свободной для размещения проводников обмотки, м2:
Контролем правильности размещения обмотки в пазах является значение коэффициента заполнения паза:
, (34)
где dиз – диаметр изолированного элементарного проводника, мм. dиз=1.33*10-3 м.
Коэффициент заполнения входит в указанные пределы (0.72< <0.74)[1]
Для обмотки статора используется круглый медный эмалированный провод ПЭТ-155 с площадью поперечного сечения 1.227 мм2.
2.4 Расчёт ротора
На следующем этапе выбирается воздушный зазор по рис. 8,31 [1, c.300]:
= 0,0007 (м)
После выбора величины воздушного зазора выполняется расчёт короткозамкнутого ротора.
Число пазов ротора по таблице 8.16 [1, c.307]: .
Диаметр ротора:
(35)
Длина магнитопрвода ротора равна длине магнитопровода статора: .
Зубцовое деление:
(36)
Внутренний диаметр ротора равен диаметру вала, так как сердечник ротора непосредственно насаживается на вал, по формуле 8.102 [1, c.319]:
; (37)
где – находим из таблицы 8.17 [1, c.319].
(м).
Коэффициент привидения токов по формуле 8.66 [1, c.308]
, (38)
Пазы ротора со скосом пазов вычисляем по формулам.
(39)
(40)
Угол скоса:
(41)
Коэффициент скоса равен:
(42)
Ток в обмотке ротора по формуле 8.57 [1, c.302]
, (43)
где – коэффициент учитывающий влияние формы тока намагничивания на отношение I2/I1 находим по формуле 8.58 [1, c.303]
. (45)
Плотность поперечного сечения стержня предварительно по формуле 8.68 [1, c.308], плотность тока в стержне алюминиевой литой клетки принимаем
(46)
2.5 Расчёт паза ротора
Принимается =0,8 мм,
=1,7 мм,
=0,5 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапецеидального закрытого паза. Форма паза ротора представлена в графической части проекта.
Определяем допустимое значение индукции по таблице 8.10 [1, c.289] =1.85.
Допустимая ширина зубца по формуле 8.75 [1, c.314]
(47)
Размеры паза по формулам 8.76-8.78 [1, c.314]:
(48)
(49)
(50)
Уточняем ширину зубцов ротора по формулам таблицы 8.18 [1,c.324]
(51)
Полная высота паза:
(52)
(53)
Таким образом Площадь поперечного сечения стержня рассчитываем по формуле 8.79 [1, c. 314]
(54)
Плотность тока в стержне:
(55)
2.6 Расчёт короткозамыкающих колец
Токи в кольце по формуле 8.70 [1, c.309]
(56)
где .
Плотность тока в замыкающих кольцах [1, c.309]:
. (57)
Площадь поперечного сечения кольца по формуле 8.72 [1, c.309]:
(58)
Высота сечения кольцах [1, c.310]:
(59)
Ширина замыкающих колец [1, c.310]:
. (60)
Средний диаметр замыкающих колец по формуле 8.74 [1, c.310]:
. (61)
Следующим этапом является электромагнитный расчет.
3. Электромагнитный расчёт
3.1 Расчет магнитной цепи
Для магнитопровода используется сталь 2312.
Магнитное напряжение воздушного зазора определяется по формуле:
(62)
где – коэффициент воздушного зазора;
– магнитная постоянная.
Коэффициент воздушного зазора рассчитывается по следующей формуле:
(63)
(64)
где – зубцовое деление статора;
– ширина шлица паза статора.
Для статора =14·10-3 м,
=4·10-3 м,=0,7·10-3 м.
Далее рассматривается магнитное напряжение зубцовой зоны статора. Для зубцов с параллельными гранями (трапециидальные пазы):
, (65)
(66)
(67)
По таблице 8.15 [1, c. 299] расчетная высота паза hZ1=hп=33·10-3 м.
Индукция в зубце, Тл:
(68)
Магнитное напряжение зубцовой зоны статора, А:
(69)
После расчёта магнитной цепи статора рассчитывается магнитная цепь ротора. Общая формула для расчета магнитного напряжения ротора, А:
(70)
где – расчётная высота зубца, м;
– расчётная напряжённость в зубце, А/м.
Для короткозамкнутого ротора с закрытыми пазами
=
-0,1
=28-0,1·5.86=27 мм. (71)
Индукция в зубце, Тл:
(72)
Пусть действительная индукция =1,85 Тл, соответствующая ей напряжённость
=3330 А/м (таблица П – 17, [2, c. 330]). Полученные данные нужно подставить в следующие уравнения:
Магнитное напряжение зубцовой зоны статора, А:
(73)
Коэффициент насыщения зубцовой зоны рассчитываем по формуле 8.115 [1, c.328]:
(74)
На следующем этапе рассматривается магнитное напряжение ярма статора по формуле 8.116 [1, c.329]:
(75)
где – длина средней магнитной силовой линии в ярме статора, м;
– напряжённость поля при индукции
по кривой намагничивания стали ярма, А/м.
Индукция в ярме статора, определяется по следующей формуле, Тл:
(76)
где – расчётная высота ярма статора, м.
При отсутствии аксиальных вентиляционных каналов в статоре:
(77)
Длина средней магнитной силовой линии в ярме статора:
(78)
По таблице П – 16 [2, c. 460] для =1.1 Тл для стали 2212
=332 А/м.
Магнитное напряжение ярма ротора, А по формуле 8.121 [1, c.329]:
(79)
где – напряжённость поля в ярме при индукции
по кривой намагничивания;
– длинна силовой линии в ярме, м.
Для двигателей с непосредственной посадкой ротора на вал (Dj=DB) без вентиляционных аксиальных каналов по формуле 8.123 [1, c.330]:
(80)
Индукция в ярме ротора по формуле 8.122 [1, c.329]:
Для =0.44 Тл,
=108 А/м.
Длина средней магнитной силовой линии в ярме ротора, м:
(81)
. (82)
Суммарное магнитное напряжение на пазу полюсов по формуле 8.128 [1, c.330]:
(83)
Коэффициент насыщения магнитной цепи по формуле 8.129 [1, c.330]:
(84)
3.2 Расчёт намагничивающего тока
Намагничивающий ток по формуле 8.130 [1, c.331]:
(85)
Относительное значение намагничивающего тока определяется по формуле 8.131 [1, c.331]:
(86)
– находится в допустимых пределах
На следующем этапе рассчитываются параметры асинхронной машины для номинального режима.
3.3 Параметры рабочего режима
Для номинального режима АД активное сопротивление обмотки статора определяется по формуле 8.132 [1, c.332]:
(87)
где – общая длинна эффективных проводников фазы обмотки, м;
– площадь поперечного сечения эффективного проводника, м2;
– удельное сопротивление материала обмотки при расчётной температуре,Ом·м;
-коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока.
Значение для номинальных режимов принимается равным единице. Для класса изоляции F
=(1/41)·10-6 Ом·м.
Общая длина проводников фазы обмотки определяется по формуле:
(88)
где – средняя длина витка обмотки статора, м;
– число витков фазы.
Средняя длинна витка есть сумма прямолинейных пазовых и изогнутых лобовых частей катушки:
(89)
Длина пазовой части равна конструктивной длине сердечника, для всыпной обмотки статора длина лобовой части равна:
(90)
Вылет лобовых частей, м:
(91)
где – средняя ширина катушки, м, определяемая по дуге окружности, проходящей по серединам высоты пазов; B – длины вылета прямолинейной части катушек из паза, м.
, (92)
где – относительное укорочение шага обмотки статора.
,
– коэффициенты в зависимости от числа полюсов машины и наличия изоляции в лобовых частях (таблица 8.21[1, с.334]).
Для машин, обмотки которых укладываются после запрессовки сердечника в корпус, вылет прямолинейной части B=0,01 м. Из таблицы 8.21 [1, с. 334] =1,9,
=0,72.
(м),
(м),
(м),
(м),
(м).
Активное сопротивление фазы статора:
(Ом).
Относительное значение:
(93)
Далее рассчитывается активное сопротивление фазы ротора, Ом:
(94)
где -сопротивление стержня;
– сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями.
Сопротивление стержня:
(95)
Сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями:
. (96)
Для дальнейших расчётов должно быть приведено к числу витков первичной обмотки:
. (97)
( Ом).
Относительное значение сопротивления:
(98)
Далее рассчитываются индуктивные сопротивления, обмоток статора и ротора двигателя.
Индуктивное сопротивление фазы обмотки статора:
(99)
где – расчётная длина магнитопровода, м;
– коэффициенты магнитной проводимости пазового, лобового и дифференциального рассеяния соответственно.
При отсутствии вентиляционных каналов =
,
=
=1,
=0.024.
Коэффициент рассчитывается для двухслойной обмотки в трапециидальном пазу.
(100)
Коэффициент магнитной проводимости лобового рассеяния:
(101)
Коэффициенты магнитной проводимости дифференциального рассеяния:
(102)
(103)
Из рисунка 8.51 [1, c. 340] =0,9
=1.
.
Относительное значение:
(104)
Индуктивное сопротивление фазы обмотки ротора по 8.177 [1, c.343]:
(105)
где – коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора;
– коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора;
– коэффициент магнитной проводимости лобового рассеяния ротора.
(106)
так как режим номинальный.
Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора:
(107)
Коэффициент магнитной проводимости лобового рассеяния для ротора с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора:
(108)
Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора:
(109)
Приводим к числу витков статора по формуле:
(110)
Относительное значение:
(111)
На следующем этапе проектирования рассчитываются потери и КПД.
3.4 Расчет потерь
Основные потери в стали определяются по формуле:
(112)
где – удельные потери, Вт/кг; – показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания, =1,5;
,
– коэффициенты, учитывающие влияние на потери в стали, неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов;
,
– масса стали ярма и зубьев статора, кг. Для стали 2312 по таблице 8.26 [1, c. 348] принимается
=1,3 Вт/кг. Для машины мощностью менее 250 кВт
=1,6 и
=1,8.
(113)
(114)
где =
– расчётная высота зубца статора, м;
– удельная плотность стали,
=7800 кг/м3.
Затем рассчитываются добавочные потери в стали.
Амплитуда пульсации индукции в воздушном зазоре над коронками зубцов статора и ротора, Тл:
(115)
.
=0,16 из рисунка 8.53 [1, c.349].
По и частоте пульсаций индукции под зубцами, равной
, определяются удельные поверхностные потери для ротора. Для проектируемого двигателя n=600 мин-1.
(116)
где – коэффициент учитывающий влияние обработки поверхности зубцов ротора на удельные потери.
Принимается =1,5.
Полные потери ротора, Вт:
(117)
Для определения пульсационных потерь вначале находится амплитуда пульсаций индукции в среднем сечении зубцов ротора, Тл:
(118)
.
Пульсационные потери в зубцах статора и ротора, Вт:
(119)
Масса стали зубцов ротора:
(120)
Добавочные потери в стали, Вт:
, (121)
Полные потери в стали, Вт:
(122)
Механические потери, Вт:
(123)
(124)
Добавочные потери, Вт при номинальном режиме:
(125)
Суммарные потери в двигателе ,Вт:
(126)
Коэффициент полезного действия двигателя:
(127)
Рассчитываем холостой ход двигателя.
Электрические потери статора при холостом ходе, Вт:
(128)
Ток холостого хода двигателя, А:
(129)
где – активная составляющая тока, А;
– реактивная составляющая тока, А.
(130)
.
– при холостом ходе:
(131)
На следующем этапе необходимо рассчитать рабочие характеристики асинхронной машины.
3.5 Расчет рабочих характеристик
Методы расчёта характеристик основаны на системе уравнений токов и напряжений, которой соответствует схема замещения.

Рисунок 3.1- Cхема замещения.
Рассчитаем сопротивление взаимной индукции обмоток статора и ротора:
(132)
(133)
Комплексный коэффициент для машин мощностью более 3 кВт с большой точностью можно определить по формуле:
(134)
(135)
(136)
(137)
Активная составляющая тока синхронного холостого хода, А:
(138)
Номинальное скольжение (предварительно) принимаем s=0,02
Для расчёта рабочих характеристик необходимы следующие формулы:
(139)
(140)
(141)
(142)
(143)
(144)
(145)
(146)
(147)
(148)
(149)
(150)
(151)
(152)
(153)
(154)
(155)
(156)
(157)
Результаты расчёта рабочих характеристик представлены в таблице 3.4.1 и 3.4.2
Таблица 3.4.1
|
Si |
m1i |
zi |
I1ai |
I1pi |
I1i |
I2i |
P1i |
|
0.0001 |
619.587 |
619.962 |
1.577 |
37.149 |
37.18 |
0.373 |
1.041 |
|
0.0019 |
32.61 |
32.718 |
7.945 |
37.253 |
38.09 |
7.065 |
5.244 |
|
0.0038 |
16.305 |
16.417 |
14.616 |
37.563 |
40.3 |
14.081 |
9.647 |
|
0.0057 |
10.87 |
10.986 |
21.226 |
38.073 |
43.5 |
21.043 |
14.009 |
|
0.0076 |
8.152 |
8.272 |
27.767 |
38.778 |
47.69 |
27.945 |
18.326 |
|
0.0095 |
6.522 |
6.645 |
34.231 |
39.673 |
52.39 |
37.786 |
22.592 |
|
0.011 |
5.435 |
5.562 |
40.61 |
40.751 |
57.53 |
41.56 |
26.803 |
|
0.013 |
4.659 |
4.79 |
46.898 |
42.007 |
62.9 |
48.265 |
30.952 |
|
0.015 |
4.076 |
4.211 |
53.087 |
43.434 |
68.59 |
54.897 |
35.038 |
|
0.017 |
3.623 |
3.762 |
59.173 |
45.025 |
74.35 |
61.453 |
39.054 |
|
0.019 |
3.261 |
3.403 |
65.15 |
46.773 |
80.2 |
67.93 |
42.868 |
|
0.021 |
2.965 |
3.11 |
71.013 |
48.67 |
86.09 |
74.326 |
46.868 |
|
0.023 |
2.717 |
2.867 |
76.757 |
50.71 |
91.99 |
80.638 |
50.659 |
|
0.024 |
2.592 |
2.744 |
80.027 |
51.954 |
95.41 |
84.254 |
52.818 |
|
0.026 |
2.383 |
2.538 |
86.153 |
54.448 |
101.91 |
91.075 |
56.861 |
|
0.029 |
2.174 |
2.334 |
93.243 |
57.612 |
109.6 |
99.054 |
61.54 |
Таблица 3.4.2
|
Ri |
I“2i |
P2i |
P’э2i |
P’э1i |
Pдобi |
|
|
|
|
619.962 |
0.355 |
0.124 |
0.00002 |
0.411 |
0.0052 |
0.119 |
0.042 |
1.164 |
|
32.718 |
6.724 |
4.03 |
0.0084 |
0.431 |
0.026 |
0.768 |
0.209 |
1.214 |
|
16.417 |
13.401 |
8.334 |
0.033 |
0.483 |
0.048 |
0.864 |
0.363 |
1.313 |
|
10.986 |
20.026 |
12.552 |
0.075 |
0.565 |
0.07 |
0.896 |
0.487 |
1.458 |
|
8.272 |
26.595 |
16.679 |
0.131 |
0.676 |
0.092 |
0.91 |
0.582 |
1.647 |
|
6.645 |
33.105 |
20.711 |
0.204 |
0.816 |
0.113 |
0.917 |
0.653 |
1.881 |
|
5.562 |
39.553 |
24.646 |
0.291 |
0.984 |
0.134 |
0.92 |
0.706 |
2.157 |
|
4.79 |
45.933 |
28.479 |
0.392 |
1.178 |
0.155 |
0.92 |
0.745 |
2.473 |
|
4.211 |
52.245 |
32.208 |
0.507 |
1.399 |
0.175 |
0.919 |
0.774 |
2.829 |
|
3.762 |
58.484 |
35.832 |
0.636 |
1.644 |
0.195 |
0.917 |
0.796 |
3.223 |
|
3.403 |
64.648 |
39.347 |
0.77 |
1.912 |
0.215 |
0.915 |
0.812 |
3.652 |
|
3.11 |
70.735 |
42.753 |
0.93 |
2.203 |
0.234 |
0.912 |
0.825 |
4.116 |
|
2.867 |
76.743 |
46.048 |
1.095 |
2.516 |
0.253 |
0.909 |
0.834 |
4.612 |
|
2.744 |
80.184 |
47.904 |
1.195 |
2.706 |
0.264 |
0.907 |
0.839 |
4.913 |
|
2.538 |
86.675 |
51.345 |
1.396 |
3.088 |
0.284 |
0.903 |
0.845 |
5.517 |
|
2.334 |
94.269 |
55.261 |
1.652 |
3.571 |
0.308 |
0.989 |
0.851 |
6.279 |

3.6 Расчет пусковых характеристик
Расчет токов с учетом влияния изменения параметров под влиянием эффекта вытеснения тока (без учета влияния насыщения от полей рассеяния).
Расчет проводим для значения s=1.
Находим высоту стержня по рисунку 2.1:
(158)
При литой алюминиевой обмотке ротора при расчетной температуре 75o имеем по 8.244 [1, c.364]:
(159)
Находим параметры для =1.76 из графиков на рисунках 8.57-58 [1, c. 366]:
;
Глубина проникновения тока по формуле 8.246 [1, c.367]:
(160)
Тогда площадь сечения по 8.253 [1, c.367]:
(161)
(162)
.
Коэффициент определяется по формуле 8.247 [1, c.365]:
(163)
Коэффициент общего увеличения сопротивления фазы ротора под влиянием вытеснения тока по 8.257 [1, c.368]:
(164)
Приведенное активное сопротивление фазы ротора под действием эффекта вытеснения тока по 8.260 [1, c.369]:
(165)
Коэффициент магнитной проводимости пазового рассеяния с учетом вытеснения тока:
(167)
Рассчитываем коэффициент уменьшения индуктивного сопротивления фазы ротора:
(168)
Приведенное индуктивное сопротивление фазы ротора под действием эффекта вытеснения тока по 8.260 [1, c.369]:
(169)
Пусковые параметры:
(170)
(171)
. (172)
(173)
Токи без учета влияния эффекта насыщения:
(174)
(175)
Расчет токов с учетом влияния вытеснения тока и насыщения от полей рассеяния.
Зададимся кратностью увеличения тока, обусловленного уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны:
. (176)
Средняя МДС обмотки, отнесенная к одному пазу статора:
; (177)
Фиктивная индукция потока рассеяния:
(178)
где коэффициент, который находится следующим образом:
(179)
По рисунку 8.61 [1, c.370] выбираем для =3.4
.
Значение дополнительного раскрытия паза статора:
(180)
Уменьшение коэффициента магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.266 [1, c.371]:
(181)
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.271 [1, c.372]:
(182)
Коэффициент проводимости дифференциального рассеяния участков зубцов статора с учетом влияния насыщения по 8.274 [1, c.373]:
(183)
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния:
(184)
Значение дополнительного раскрытия паза ротора:
(185)
Уменьшение коэффициента магнитной проводимости пазового рассеяния обмотки ротора с учетом влияния насыщения по 8.271 [1, c.371]:
(186)
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.271 [1, c.372]:
(187)
Коэффициент проводимости дифференциального рассеяния участков зубцов ротора с учетом влияния насыщения по 8.274 [1, c.373]:
(188)
Приведенное индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния:
(189)
Пусковые параметры:
(190)
(191)
(192)
Ток в обмотке ротора:
(193)
Ток в обмотке статора:
(194)
Кратность пускового тока:
(195)
Кратность пускового момента:
(196)
Формулы для расчета токов в пусковом режиме асинхронного двигателя с КЗ ротором с учетом эффекта вытеснения тока.
(197)
. (198)
(199)
(200)
(201)
(202)
(203)
(204)
(205)
(206)
(207)
(208)
(209)
(210)
(211)
Результаты расчёта токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока представлены в таблице 3.5.1 и 3.5.2
Таблица 3.5.1 – Расчет токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока
|
Si |
|
|
hri |
kri |
Kri |
|
|
|
1 |
1.743 |
0.55 |
0.018 |
1.43 |
1.34 |
0.075 |
0.8 |
|
0.8 |
1.559 |
0.42 |
0.019 |
1.32 |
1.25 |
0.07 |
0.9 |
|
0.6 |
1.35 |
0.309 |
0.021 |
1.22 |
1.17 |
0.066 |
0.9 |
|
0.5 |
1.233 |
0.259 |
0.022 |
1.18 |
1.14 |
0.064 |
0.9 |
|
0.4 |
1.102 |
0.213 |
0.023 |
1.14 |
1.11 |
0.062 |
0.95 |
|
0.35 |
1.031 |
0.193 |
0.023 |
1.12 |
1.09 |
0.061 |
0.95 |
|
0.3 |
0.955 |
0.173 |
0.023 |
1.103 |
1.08 |
0.061 |
0.95 |
|
0.25 |
0.872 |
0.156 |
0.024 |
1.09 |
1.07 |
0.06 |
0.95 |
|
0.2 |
0.78 |
0.14 |
0.024 |
1.07 |
1.058 |
0.059 |
0.97 |
|
0.151 |
0.677 |
0.126 |
0.024 |
1.06 |
1.05 |
0.059 |
0.97 |
|
0.146 |
0.666 |
0.125 |
0.024 |
1.06 |
1.048 |
0.059 |
0.97 |
|
0.1 |
0.551 |
0.114 |
0.025 |
1.05 |
1.041 |
0.058 |
0.97 |
|
0.05 |
0.39 |
0.105 |
0.025 |
1.044 |
1.034 |
0.058 |
0.99 |
|
0.001 |
0.055 |
0.1 |
0.025 |
1.04 |
1.031 |
0.058 |
0.99 |
Таблица 3.5.2
|
Si |
|
Kxi |
|
Xni |
I`2i |
I1i |
Rni |
|
1 |
1.474 |
0.929 |
0.173 |
0.466 |
441.351 |
451.6 |
0.177 |
|
0.8 |
1.6 |
0.964 |
0.18 |
0.473 |
431.68 |
442.1 |
0.19 |
|
0.6 |
1.6 |
0.964 |
0.18 |
0.473 |
424.233 |
434.5 |
0.213 |
|
0.5 |
1.6 |
0.964 |
0.18 |
0.473 |
4117.8 |
427.9 |
0.232 |
|
0.4 |
1.662 |
0.982 |
0.183 |
0.476 |
405.3 |
415.3 |
0.26 |
|
0.35 |
1.662 |
0.982 |
0.183 |
0.476 |
397.8 |
407.7 |
0.281 |
|
0.3 |
1.662 |
0.982 |
0.183 |
0.476 |
387.5 |
397.3 |
0.309 |
|
0.25 |
1.662 |
0.892 |
0.183 |
0.476 |
372.9 |
382.4 |
0.348 |
|
0.2 |
1.687 |
0.989 |
0.185 |
0.478 |
350.5 |
359.6 |
0.41 |
|
0.151 |
1.687 |
0.989 |
0.185 |
0.478 |
316.9 |
325.4 |
0.5 |
|
0.146 |
1.687 |
0.989 |
0.185 |
0.478 |
312.3 |
320.8 |
0.52 |
|
0.1 |
1.687 |
0.989 |
0.185 |
0.478 |
258.3 |
265.6 |
0.71 |
|
0.05 |
1.712 |
0.996 |
0.186 |
0.479 |
158.3 |
164.4 |
1.3 |
|
0.001 |
1.712 |
0.996 |
0.186 |
0.479 |
3.657 |
28.4 |
60.2 |
Формулы для расчета токов в пусковом режиме асинхронного двигателя с КЗ ротором с учетом эффектов вытеснения и насыщения.
. (212)
(213)
(214)
(215)
(216)
(217)
(218)
(219)
(220)
(221)
Пусковые параметры:
(222)
(223)
(224)
(225)
(226)
(227)
(228)
Результаты расчёта токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока представлены в таблице 3.5.3 и 3.5.4.
Таблица 3.5.3 – Расчет пусковых характеристик асинхронного двигателя с КЗ ротором учетом эффекта вытеснения тока и насыщения от полей рассеяния
|
|
|
|
|
|
|
|
|
|
|
1 |
1.35 |
4013 |
3.432 |
0.68 |
0.0031 |
0.246 |
1.033 |
1 |
|
0.8 |
1.3 |
3783 |
3.235 |
0.68 |
0.0031 |
0.246 |
1.033 |
0.8 |
|
0.6 |
1.25 |
3575 |
3.057 |
0.68 |
0.0031 |
0.246 |
1.033 |
0.6 |
|
0.5 |
1.25 |
3521 |
3.011 |
0.68 |
0.0031 |
0.255 |
1.033 |
0.5 |
|
0.4 |
1.15 |
3144 |
2.689 |
0.75 |
0.0024 |
0.255 |
1.034 |
0.4 |
|
0.35 |
1.15 |
3086 |
2.639 |
0.75 |
0.0024 |
0.255 |
1.034 |
0.35 |
|
0.3 |
1.15 |
3007 |
2.572 |
0.75 |
0.0024 |
0.261 |
1.034 |
0.3 |
|
0.25 |
1.15 |
2894 |
2.475 |
0.3 |
0.0019 |
0.261 |
1.035 |
0.25 |
|
0.2 |
1.05 |
2485 |
2.125 |
08 |
0.0019 |
0.279 |
1.035 |
0.2 |
|
0.151 |
1.05 |
2249 |
1.923 |
0.95 |
0.00049 |
0.279 |
1.037 |
0.151 |
|
0.146 |
1.05 |
2217 |
1.896 |
0.95 |
0.00049 |
0.279 |
1.037 |
0.146 |
|
0.1 |
1.05 |
1836 |
1.57 |
0.95 |
0.00049 |
0.283 |
1.037 |
0.1 |
|
0.05 |
1.05 |
1136 |
0.972 |
0.98 |
0.00019 |
0.283 |
1.038 |
0.05 |
|
0.001 |
1.05 |
196.5 |
0.168 |
0.98 |
0.00019 |
0.283 |
1.038 |
0.001 |
Таблица 3.5.4
|
|
|
|
|
|
|
|
|
|
|
0.537 |
0.177 |
0.385 |
519.3 |
528.69 |
1.171 |
1.033 |
1.216 |
5.541 |
|
0.563 |
0.19 |
0.39 |
505.3 |
514.9 |
1.165 |
1.033 |
1.343 |
5.39 |
|
0.563 |
0.212 |
0.392 |
493.6 |
502.9 |
1.157 |
1.033 |
1.603 |
5.27 |
|
0.563 |
0.231 |
0.392 |
483.6 |
492.8 |
1.152 |
1.033 |
1.793 |
5.165 |
|
0.601 |
0.26 |
0.41 |
453.2 |
462.5 |
1.113 |
1.034 |
1.915 |
4.848 |
|
0.601 |
0.308 |
0.41 |
442.8 |
451.9 |
1.109 |
1.034 |
2.064 |
4.737 |
|
0.601 |
0.347 |
0.41 |
428.9 |
437.8 |
1.102 |
1.034 |
2.231 |
4.589 |
|
0.621 |
0.406 |
0.421 |
403 |
411.7 |
1.077 |
1.035 |
2.338 |
4.315 |
|
0.626 |
0.503 |
0.422 |
375.4 |
383.7 |
1.067 |
1.035 |
2.509 |
4.021 |
|
0.699 |
0.517 |
0.461 |
322.4 |
330.6 |
1.016 |
1.037 |
2.431 |
3.465 |
|
0.699 |
0.71 |
0.461 |
317.7 |
325.8 |
1.016 |
1.037 |
2.44 |
3.415 |
|
0.699 |
1.3 |
0.461 |
261.3 |
268.4 |
1.01 |
1.037 |
2.392 |
2.813 |
|
0.726 |
1.5 |
0.472 |
158.7 |
164.7 |
1.002 |
1.038 |
1.754 |
1.726 |
|
0.726 |
60.137 |
0.472 |
3.658 |
28.45 |
1 |
1.038 |
0.046 |
0.298 |
Кратность максимального момента для
4 Круговая диаграмма
Круговая диаграмма представлена на листе Д1.
Круговая диаграмма изображена в графической части курсового проекта. Исходными данными для её построения являются:
Ток синхронного холостого хода по формуле 8.236 [1, стр.360]:
, (229)
А.
Коэффициент c1 = 1.0348.
Сопротивление короткого замыкания по формуле 8.237 [1,стр.360]:
, (230)
Ом;
, (231)
Ом;
Диаметр круговой диаграммы: Dk = 200 мм.
Рассчитаем масштабы.
Масштаб тока:
, (232)
А/мм.
Масштаб мощности:
, (233)
Вт/мм;
Масштаб момента:
, (234)
Н·м/м;
Вектор тока синхронного холостого хода:
, (235)
мм;
, (236)
0.
Определим длинны отрезков:
, (237)
; мм
, (238)
;м
м;
, (239)
м;
, (240), где:
, (241)
Вт.
Тогда:
мм.
По круговой диаграмме для тока статора , которому соответствует точка А на окружности, можно рассчитать необходимые для построения рабочих характеристик данные:
1. Ток статора, А: , (242)
2. Ток ротора, А: , (243)
3. Первичная мощность, Вт: , (244)
4.Электромагнитныймомент: (245)
5. Полезная мощность, Вт: ; (246)
6. КПД: ; (247)
7. Коэффициент мощности: ,
8.Скольжение двигателя: . (248)
Полученная круговая диаграмма представлена в графической части проекта.
5 Тепловой и вентиляционный расчеты
5.1 Тепловой расчет
Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри двигателя:
(249)
где K=0,17 – коэффициент, определяемый из таблицы 8.33 [1, c.402]; =74 – коэффициент теплоотдачи по рисунку 8.71 [1, c.401];
– электрические потери в пазовой части статора.
(250)
Перепад температуры в изоляции пазовой части обмотки статора по 8.331 [1, c.400]:
(251)
где – расчетный параметр поперечного сечения паза статора;
– средняя эквивалентная теплопроводность изоляции класса B;
– среднее значение коэффициента теплопроводности внутренней изоляции обмотки из эмалированных проводников с учетом неплотности прилегания проводников друг к другу по рисунку 8.72 [1, c.402].
(252)
=0,16 Вт/м2 .
=1,4 Вт/м2 .
Перепад температуры по толщине изоляции лобовых частей по 8.335 [1, c.402]:
(253)
где – расчетный параметр поперечного сечения паза статора;
– электрические потери в лобовых частях статора.
(254)
=0.05
Повышение температуры наружной поверхности лобовых частей над температурой воздуха внутри двигателя:
(255)
Среднее превышение температуры обмотки статора над температурой воздуха внутри двигателя:
(256)
Превышение температуры воздуха внутри двигателя над температурой окружающей среды по 8.338 [1, c.403]:
(257)
где – эквивалентная поверхность охлаждения;
– коэффициент подогрева воздуха, определяется по рисунку 8.70 [1 c. 400];
– сумма потерь, отводимых в воздух двигателя.
Вт/
(258)
(259)
=1,07 – коэффициент нагревостойкости.
(260)
Среднее превышение температуры обмотки статора над температурой окружающей среды по 8.344 [1, c.404]:
(261)
5.2 Вентиляционный расчет
Для двигателей со степенью защиты IP44, требуемый для охлаждения расход воздуха вычисляется по формуле 8.356 стр. 407 [1]:
м3/с, (262)
где – коэффициент, учитывающий изменение условий охлаждения по всей длине поверхности корпуса, вычисляется по формуле 8.357 стр. 407 [1]:
м3/с, (263)
-Коэффициент, зависящий от высоты вращения и числа пар полюсов стр. 407 [1].
Определяем расход воздуха, обеспечиваемый наружным вентилятором по формуле 8.358 стр. 407 [1]:
м3/с. (264)
Т.к. , то требуемый для охлаждения объем воздуха наружным вентилятором обеспечивается.
Принимаем . По выбранному диаметру вентилятора мы определяем окружную скорость по формуле 7.49 стр. 236 [1]:
(265)
Номинальный расход воздуха .
Сечение на выходной кромке вентилятора найдем по формуле 7.51 стр. 237 [1]:
. (267)
Ширина колеса вентилятора вычисляется по формуле 7.52 стр. 237 [1]:
. (268)
Выберем аэродинамическое сопротивление по рисунку 7.5 стр. 231 [1]:
Окружная скорость на внутренней кромке вентилятора по формуле 7.55 стр. 237 [1]:
. (269)
где -для радиальных лопаток стр. 237 [1].
-плотность охлаждающей среды.
Давление развиваемое вентилятором в режиме холостого хода вычисляется по формуле 7.42 стр. 234 [1]:
(270)
Рассчитаем внутренний диаметр по формуле:
(271)
Число лопаток вентилятора по формуле:
(272)
Примем число лопаток равное 26.
6.Механический расчет
6.1 Расчёт вала

Рисунок 6.1 – Вал двигателя.
Расчет вала на жесткость.
Вал имеет следующие размеры (рисунок 6.1):
Сила тяжести сердечника ротора с обмоткой и участком вала по его длине по формуле 8 [3, c.17]:
Массу ротора можно представить как:
(кг) (273)
Расчет прогиба вала проводят исходя из приведенной силы тяжести
(H) (274)
Hоминальный вращающий момент для двигателя:
(275)
Прогиб вала посредине сердечника ротора от реакции передачи по формуле 9 [3, c.17]:
(H). (276)
Модуль упругости E=2,06 Па.
Момент инерции находим по формуле 13 [3, c.17]:
(277)
Для определения прогиба вала рассчитываем вспомогательные значения ,
,
по формулам 10, 11, 12 [3, c.17]:
(278)
(278)
(280)
(281)
Прогиб вала посредине сердечника ротора от реакции передачи по формуле 9 [3, c.17]:
(282)
Прогиб вала посредине сердечника ротора под действием силы тяжести по формуле 7 [3, c.15]:
Начальный расчетный эксцентриситет ротора по формуле 13 [3, c.17]:
(283)
Начальная сила одностороннего магнитного притяжения по формуле 14 [3, c.18]:
(284)
Прогиб вала под действием силы по формуле 16 [3, c.18]:
(285)
Установившийся прогиб вала от одностороннего магнитного притяжения по формуле 17 [3, c.18]:
(286)
(287)
Результирующий прогиб вала от силы тяжести ротора, реакции передачи и магнитного притяжения по формуле 18 [3, c.18]:
(288)
Суммарный прогиб вала посредине магнитопровада ротора в процента
. (289)
Прогиб составляет примерно 3.51% воздушного зазора, т.е. прогиб не влияет на вал.
Критическая частота вращения:
(290)
Превышение критической частоты вращения относительно номинальной
(291)
Рабочая частота вращения ротора отличается от критической более чем 45 раза.
В расчете на прочность принимаем коэффициент перегрузки: k=2;
Напряжение на свободном конце вала в сечении А:
Момент сопротивления при изгибе :
(292)
Напряжение в сечении Б :
(294)
Момент сопротивления при изгибе:
(295)
(296)
Напряжение в сечении В :
(297)
Момент сопротивления при изгибе :
(298)
Напряжение в сечении Г
(300)
Момент сопротивления при изгибе
Напряжение в сечении Д:
Момент сопротивления при изгибе :
Напряжение в сечении Е:
Момент сопротивления при изгибе :306
Из сопоставлениия полученных данныч следует, что наиболее нагруженным является сечение Б, для которого
выполняется условие нагруженности.
В соответствии с рекомендациями, выбираем для P=18,8 кВт со стороны выходного вала подшипники качения роликовые,а с другой стороны шариковые.
6.2 Выбор подшипников
В соответствии с рекомендациями, выбираем для P=47.8 кВт со стороны выходного вала подшипники качения роликовые, а с другой стороны шариковые.
Определяем радиальную нагрузку на подшипники RA, RB по формуле 26 [3, c.24]:
(309)
(310)
Динамическая приведенная нагрузка по формуле 27 [3, c.24]:
(311)
(312)
Динамическая грузоподъемность по формуле 27 [3, c.24]:
(313)
(314)
Выбираем по каталогу, с учетом надежности шарикоподшипник № 218 средней серии со значением С=75500 Н, роликоподшипник № 22218 средней узкой серии со значением С=55500 Н.
7 Экономический расчёт
Масса меди статора:
(315)
где – плотность меди.
=8900 кг/м3.
(316)
Масса статора:
(317)
Масса стали ротора:
(318)
где – плотность стали.
=7800 кг/м3.
(319)
Масса алюминия ротора:
(320)
где – плотность алюминия.
=2700 кг/м3.
Масса ротора:
(321)
Масса корпуса электродвигателя:
(322)
где – толщина корпуса;
– длина корпуса двигателя.
=0.02.
=0.7
(323)
Масса подшипников:
Масса подшипниковых щитов:
(324)
где – внешний диаметр подшипникового щита;
– ширина подшипникового щита.
=0.45.
=0.005.
(325)
Масса выводной коробки
Масса вала:
Масса электродвигателя:
(327)
Отношение массы к полезной мощности:
(328)
8 Описание технологии сборки
Сердечник статора и ротора шихтуются из электротехнической стали толщиной 0,5 мм, сердечник выполняется без вентиляционных каналов.
Для изоляции листов друг от друга их лакируют. Для стали 2312 листы подвергают термообработке, в результате которой стабилизируются потери в стали и образуется поверхностный оксидный изолирующий слой.
Магнитопровод ротора насаживается непосредственно на гладкий вал.
Для предотвращения деформации (распушения) относительно тонких листов крайние торцевые листы магнитопровода штампуют из более тонких листов стали.
Собранный таким образом магнитопровод прессуют. После укладки обмотки в статор и пропитки ее лаком сердечник запрессовывают в станину.
Обмотки короткозамкнутых роторов не имеют изоляции. Они выполняются заливкой пазов алюминием, причем одновременно со стержнями обмотки отливают замыкающие кольца с вентиляционными лопатками.
На ротор напрессовывают подшипники, заводят его в статор. После этого устанавливают передний фланец и фиксируют в нем подшипник ротора. Затем устанавливают задний подшипниковый щит.
После этого устанавливают на задний конец вала надевают крыльчатку вентилятора. Затем защищают вентилятор кожухом.
На завершающем этапе сборки устанавливают клемную коробку.
Перед пробным пуском проверяют точность установки вала путем прокручивания его на несколько оборотов.
К корпусу ЭД с помощью болтов на коробку выводов крепится верхняя крышка.
Заключение
В результате проектирования был разработан асинхронный двигатель с короткозамкнутым ротором, который полностью отвечает требованиям, поставленным в курсовом проекте. Все проверяемые параметры отвечают критериям, рекомендуемым ГОСТ. Из-за перехода на меньшую высоту оси вращения, разработанный двигатель по некоторым технико-экономическим параметрам уступает существующим двигателям аналогичной мощности.
Список литературы
-
Проектирование электрических машин: Учебник для вузов Книга 1. Под редакцией Копылова И.П.Москва: Энергоатомиздат 1993. – 464 с.
-
Проектирование электрических машин: Учебник для вузов Книга 2. Под редакцией Копылова И.П.Москва: Энергоатомиздат 1993. – 384 с.
-
Электрические машины. Методические указания по курсовому проектированию для студентов специальности Т.11.02.00 “Автоматизированный электропривод”.- Могилев: УО МГТУ, 2002. – 51 с.
-
Электрические машины: Асинхронные машины: Учеб. Для электромех. спец. вузов/ Радин В.И., Брускин Д.Э., Зорохович А.Е.; Под ред. И.П. Копылов-М.: Высшая школа, 1988,-328 с.
масса платформы; масса ротора; масса дисбаланса; центробежный момент ротора; эксцентриситет
Работа добавлена на сайт samzan.net: 2016-03-30
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой – мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
ТЕОРЕТИЧЕЧКАЯ ЧАСТЬ
Постановка задачи
Исследуемый объект: тело, с установленным на ней источником возбуждения (двигателем), имеющим дисбаланс.
масса платформы;
масса ротора;
масса дисбаланса;
центробежный момент ротора;
эксцентриситет.
Методом продолжения по параметру необходимо получить зависимость изменения скорости вращения ротора от напряжения питания двигателя , являющегося управляющим параметром.
Решение задачи
Приведем на рисунке 1 зависимость электрического момента и момента сопротивления от приведенной скорости вращения ротора.
Рисунок 1 – Зависимость моментов, действующих на ротор от скорости его вращения
электрический момент, действующий на ротор,
момент сопротивления,
приведенная скорость вращения ротора.
На рисунке 1 показано, что, меняя напряжение питания двигателя, характеристика ротора – двигается.
Момент, действующий на ротор , можно определить в зависимости от скорости вращения ротора , как:
|
. |
Причем номинальный режим работы, возникает при условии, что .
Уравнения движения системы
Уравнения движения исследуемой системы составим с помощью уравнения Лагранжа.
Запишем функцию Лагранжа и обобщенные силы:
Составим уравнения Лагранжа с учетом соотношения :
Нормализуем систему при следующих условиях:
где безразмерное время;
радиус инерции ротора;
безразмерный эксцентриситет.
Тогда система уравнений примет вид:
Определение периодических решений в системе уравнений
Пусть неизвестный период.
Вектор состояния .
орбитальная переменная.
Условие периодичности имеет вид:
|
, |
В случае, если монотонная функция, т.е. , то можно взять в качестве независимой переменной:
Тогда переходим к переменной Ван-дер-Поля
Выражения требуют условия совместности:
.
Запишем систему уравнений в переменных Ван-дер-Поля
Запишем систему уравнений в новых переменных:
, ,
где:
Тогда система уравнений примет вид
Введем новый вектор переменных :
|
. |
Для определения времени необходимо уравнение
Функции явно зависят от , т.е. система уравнений стала неавтономной.
Тогда условие периодичности в новых переменных имеет следующий вид:
|
. |
Виды расчетов при решении уравнения
1. Начальная задача
Известен вектор переменных при :
.
Далее решается уравнение .
2. Определение периодических решений, исследование их устойчивости.
3. Построение ветвей периодических решений методом продолжения.
На рисунке 2 изображена линия периодических решений (красная) в пространстве фазовых переменных.
Рисунок 2 – Определение периодических движений
Метод Ньютона для определения периодических движений
Обозначим:
Условие периодичности:
Далее записываем процедуру метода Ньютона, где неизвестной является .
Имеем начальное приближение , далее итерациями метода Ньютона определяем: .
Задаемся точностью , условием окончания:
ая итерация, .
Определяем поправку .
Если , то
где Это матрица Коши динамической системы, вычисленная в конце периода.
Матрица Коши линеаризованной системы при .
Методом Ньютона можно получить решение, изображенное на рисунке 3 жирной линией. Для определения кривой, на рисунке изображенной пунктиром, необходимо воспользоваться методом продолжения по параметру.
Рисунок 3 – Определение зависимости скорости от напряжения
Метод продолжения по параметру
Преобразуем систему уравнений , с помощью и введем новый вектор переменных :
,
|
. |
Таким образом, система уравнений неавтономна.
Пусть вектор неизвестных при
.
Выберем в качестве параметра длину дуги , изображенную на рисунке 4.
Рисунок 4 – К методу продолжения по параметру
Система уравнений составляют 4 уравнения, где неизвестными являются и , а является независимой переменной.
Решение этой системы уравнений называется непрерывным продолжением по параметру:
Перепишем систему уравнений в следующем виде:
Приведем систему к нормальной форме Коши:
|
. |
В том случае, когда в методе Ньютона вырождено, то невырождена.
Движение по дуге – самое устойчивое.
В случае применения метода трапеций к выражению , получим:
В выражении мы не знаем, а длина отрезка, соединяющего точки и .
Далее решение происходит методом простой итерации:
Определим следующим образом, с учетом того, что в точке известно все.
Принимаем, что , и определяем .
В ой точке известно , по нему определяем .
– определяется точкой, где сфера протыкается линией , как показано на рисунке 5.
Рисунок 5 – Определение
ПРАКТИЧЕСКАЯ ЧАСТЬ
Начальная задача
Приведем 2 расчета задачи при следующих значениях параметров системы:
На рисунке 6 представим переменные в зависимости от времени.
Рисунок 6 – Зависимость от времени
Из рисунка видно, что угловая скорость – колеблется
На рисунке 7 изобразим рабочую характеристику двигателя
Рисунок 7 – Рабочая характеристика двигателя
На рисунке 8 изобразим фазовую траекторию движения тележки и зависимость момента от времени.
Рисунок 8 – Фазовая траектория движения тележки и зависимость
На рисунке 9 изобразим нарастание угла поворота во времени.
Из рисунка 9 видно, что двигатель настолько мощный, что нарастание угла поворота происходит линейно.
Рисунок 9 – Нарастание угла поворота во времени
Для сравнения приведем результаты решения задачи для маломощного двигателя со следующими параметрами:
На рисунке 10 представим переменные в зависимости от времени и зависимость
Рисунок 10 – Зависимость от времени и
На рисунке 11 представим фазовую траекторию и зависимость угла поворота от времени.
Рисунок 11 – Фазовая траектория и угол поворота во времени
Из приведенных результатов для маломощного двигателя видно, что двигателю не хватает мощности, чтобы без колебаний справится с моментом сопротивления.
Определение периодических решений методом Ньютона
Определим периодические решения методом Ньютона для параметров и .
В случае найдено устойчивое периодическое решение.
На рисунке 12 приведем мультипликаторы.
Рисунок 12 Исследование устойчивости периодического решения
На рисунке 13 приведем зависимости от и пересчитанные по ним от .
Рисунок 13 – Зависимость от и от
На рисунке 14 приведем фазовую траекторию устойчивого решения, рабочий диапазон работы двигателя и изменение мощности во времени.
Рисунок 14 – Фазовую траектория устойчивого периодического движения, диапазон работы двигателя и изменение мощности во времени
Для системы с параметрами периодических решений не удалось найти.
Построение зависимости угловой скорости от напряжения и L -кривой
Методом Ньютона определим несколько периодических решений в системе уравнений и построим в фазовом пространстве эти решения. Изобразим их на рисунке 15.
Рисунок 15 – Периодические решения в системе уравнений
На верхнем рисунке представлены периодические решения: зависимость угловой скорости от угла поворота в зависимости от напряжения питания, на нижнем рисунке представлены периодические решения для тележки. Из рисунков видно, что после перехода напряжения питания через некоторый уровень, , сильно увеличилась скорость вращения двигателя, и заметно снизился уровень вибрации тележки (платформы).
На рисунке 16 представим мультипликаторы периодических движений и их начальные значения периодических решений.
Рисунок 16 – Мультипликаторы периодических движений и начальные значения периодических решений
На рисунке 17 представим зависимость угловой скорости от угла поворота ротора и зависимость угловой скорости, от напряжения питания.
Рисунок 17 – Зависимость угловой скорости от угла поворота ротора и зависимость угловой скорости, от напряжения питания
Получим петлю гистерезиса в области срыва электродвигателя, рисунок 18
Рисунок 18 – Определение петли гистерезиса в области срыва двигателя





