Как определить массу тела, зная силу тяжести и ускорение свободного падения?
Найдите правильный ответ на вопрос ✅ «Как определить массу тела, зная силу тяжести и ускорение свободного падения? …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Физика » Как определить массу тела, зная силу тяжести и ускорение свободного падения?
В статье обсуждаются несколько подходов и некоторые примеры проблем о том, как вычислить массу по гравитационной силе.
Каждый объект с массой во Вселенной оказывает гравитационное воздействие на другой. Вот почему сила тяжести прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Узнайте больше о Как рассчитать массу по силе и расстоянию.
Как рассчитать массу по гравитационной силе, используя второй закон движения Ньютона

Рассчитаем массу, используя второй закон движения Ньютона:
Во втором законе движения Ньютон описывает, что сила действует на объект с ненулевой массой, чтобы ускорить его в том же направлении. Гравитационная сила – это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил которые действуют на тела. гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ма ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется в соответствии со вторым законом движения. Ускорение, вызванное силой тяжести, постоянно, называется ускорение силы тяжести ‘грамм’. Поскольку гравитация всегда действует на нас, возникла идея нашего «веса» как «mg», который включает нашу массу m и ускорение «a». По этой причине гравитационную силу также называют силой тяжести. сила веса.

(Кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает следующий вид:
Fg = мг …………………………. (1)
Согласно уравнениям (*) и (1),
Чтобы поднять более тяжелое тело, мы должны создать восходящую силу (ма), превышающую силу тяжести (мг).
Поскольку g имеет постоянное значение 9.8 м / с2, гравитационная сила Fg зависит только от массы объекта m. Чем массивнее объект, тем больше силы требуется для его ускорения.
Если к объекту приложена сила тяжести, мы можем вычислить его массу по формуле второго закона движения Ньютона..
Узнайте больше о Законы движения Ньютона.
Сила тяжести, действующая на бегающую в парке девушку, равна 490. Вычислите массу девушки.
Данный:
Fg = 490 Н
g = 9.8 м / с
Найти: м =?
Формула:
F = ma
Решение:
Масса девушки рассчитывается с помощью Второй закон движения Ньютона формула,
F = ma
Компания сила гравитации дан кем-то,
Fg = мг
m=Fg/g
м=490/9.8
m = 50 кг …………………………………. а)
Масса бегущей в парке девушки 50 кг.
Как найти массу с гравитационной силой и радиусом?
Давайте вычислим массу с гравитационной силой, используя закон тяготения Ньютона следующим образом:
Закон тяготения обнаруживает, что гравитационная сила между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами масс. Если второй объект – Земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону всемирного тяготения Ньютона,
Fg=G(мМ/р2)……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке, в основном в его центральной точке, называемой его центр масс (см). Радиус r измеряет расстояние или разделение между центрами масс двух объектов.
Небольшая масса в 1 кг, разделенная радиусом 1, испытывала небольшую гравитационную силу 6.67 x 10-11 Нм.2/ кг2, совместимый с каждым объектом. Следовательно, это постоянное значение является значением постоянной пропорциональности в законе всемирного тяготения, также называемой величиной Универсальная гравитационная постоянная G.
Проще вычислить Fg между объектом и Землей как планетой с фиксированной массой M = 5.98 x 1024 кг, а также фиксированный радиус r от центра земли, r = 6.38 x 106m
Сила тяжести, действующая на девушку, бегающую трусцой в парке, равна 490. Вычислите массу девушки, используя закон всемирного тяготения Ньютона.
Данный:
Fg = 490 Н
М = 5.98 х 1024 kg
г = 6.38 х 106m
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Решение:
Масса девушки рассчитывается по Закон всемирного тяготения Ньютона является,
Fg=G(мМ/р2)
Переставляем на массу m,
м=Fgr2/ГМ
Подставляя все значения,

Из (а) и (б) мы заметили расчетная масса с использованием второго закона Ньютона и формулы закона всемирного тяготения такая же.
Закон всемирного тяготения может применяться к двум объектам, имеющим одинаковые или разные массы.

имея разные массы
(Кредит: Shutterstock)
Сила притяжения между вами и вашим коллегой составляет 3 x 10.-7 N, когда вы оба приближаетесь на расстоянии 1 м друг от друга в школьном коридоре. Поскольку ваша масса 60 кг, рассчитайте массу вашего коллеги.
Данный:
Fg = 3 x 10-7 N
г = 1 м
m1 = 60 кг
G = 6.67 х 10-11 nm2/ кг2
Найти: м2 =?
Формула:
Fg=G(м1m2/r2)
Решение:
Масса коллеги рассчитывается по формуле Закон всемирного тяготения Ньютона является,
Fg=G(м1m2/r2)
Перестановка на массу m2,
m2=Fgr2/Гм1
Подставляя все значения,

Масса вашего коллеги 75 кг.
Как рассчитать массу по гравитационной силе, используя формулу центростремительной силы?
Рассчитаем массу с гравитационной силой, используя центростремительная сила формула следующим образом:
Когда объект движется по кругу, его скорость постоянно меняется в зависимости от его направления. Направление ускорения – к центру, вызванное центростремительной силой. Поскольку масса всего объекта сосредоточена в его центре, мы можем рассчитать ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона движения Ньютона.
Поскольку ускорение – это круговой путь, нам нужно учитывать радиус; вот почему ускорение становится
v2/r
Следовательно, согласно уравнению (*) центростремительная сила определяется как
Fc=мв2/r
Центростремительная сила – это центристская сила который действует на объект, чтобы двигаться по кругу к его центру. Земля оказывает центростремительное сила, действующая на спутник, чтобы поддерживать его круговое движение вокруг.

Спутник непрерывно движется по орбите вокруг Земли со скоростью 20 м / с. Гравитационная сила между Землей и спутником составляет 500 Н, что создает центростремительную силу около 200 Н. Вычислите массу спутника.
Данный:
Fg = 500 Н
Fc = 200 Н
v = 20 м / с
M = масса Земли = 5.98 x 1024 kg
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Fc=мв2/r
Решения:
Масса спутника рассчитывается по формуле закон всемирного тяготения Ньютона,
Fg=G(мМ/р2)
Компания центростремительная сила на спутнике есть,
Fc=мв2/r
Решая формулу для радиуса r,
г=мв2/Fc
Подставляя вышеприведенное уравнение в закон всемирного тяготения Ньютона, получаем
Fg=Fc2[ГМ/мв4]
Решая массу m,
Подставляя все значения,

м=159.4/8
м = 19.94 примерно 20 кг
Масса спутника, движущегося вокруг Земли, составляет 20 кг.
Содержание:
- Определение и формула массы тела
- Инертная масса
- Гравитационная масса
- Формула расчета массы через плотность тела
- Масса в специальной теории относительности
- Примеры решения задач
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (mi):
$$m=sum_{i=1}^{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$bar{F}=m bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (Ft) избранного тела:
$$m=frac{F_{t}}{g}(3)$$
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
$$m=int_{V} rho d V(4)$$
где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:
$m = rho V (5)$
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Примеры решения задач
Пример
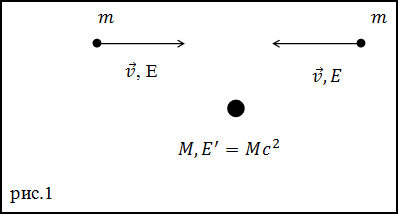
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
$$E^{prime}=M c^{2}(1.1)$$
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
