Загрузить PDF
Загрузить PDF
Шар является одним из наиболее простых трехмерных тел. Чтобы найти массу шара, необходимо знать его объем и плотность. Объем можно вычислить по радиусу, длине окружности или диаметру. Можно также погрузить шар в воду и найти объем по количеству вытесненной им воды. После того как вы определите объем, умножьте его на плотность, и вы получите массу шара.
-

1
Вспомните формулу для вычисления объема шара. Шар представляет собой трехмерное геометрическое тело. Объем шара вычисляется по следующей основной формуле:[1]
-

2
Найдите объем шара по известному радиусу. Радиус шара — это расстояние от его центра до внешнего края. Объем шара можно найти, если известен его радиус. В то же время радиус шара довольно сложно измерить из-за проблем с точным определением и достижением центра сплошного тела.[2]
-

3
Найдите объем по известному диаметру. В задаче может быть указан диаметр шара. Диаметр равен удвоенному радиусу. Иными словами, диаметр представляет собой длину отрезка, проведенного от одного края шара к другому через его центр. Чтобы вычислить объем шара по заданному диаметру (d), перепишем формулу в следующем виде:[3]
-

4
-

5
-

6
Найдите объем по вытесненной воде. Легкий метод непосредственно измерить объем шара заключается в том, чтобы погрузить его в воду. Вам понадобится достаточно большой лабораторный стакан, чтобы в него вошел шар, с нанесенными на нем метками объема.[5]
- Налейте в стакан достаточное количество воды, чтобы она полностью покрывала шар. Запишите результаты измерений.
- Опустите шар в воду. Отметьте начальный уровень воды и то, насколько она поднялась. Запишите результат.
- Вычтите начальный уровень воды из конечного. В результате вы получите объем шара.
- Предположим, при опускании шара в стакан уровень воды поднялся со 100 до 625 миллилитров. В этом случае объем шара составляет 525 миллилитров. Учтите, что 1 мл=1 см3.
Реклама
-

1
Найдите плотность. Чтобы вычислить массу по объему, необходимо знать плотность тела. Разные материалы имеют различную плотность. Сравните, например, шар из пенопласта и железа. Железо имеет намного большую плотность, поэтому железный шар будет значительно тяжелее.
- Плотность многих материалов можно определить по таблицам плотностей, которые можно найти в интернете, справочнике или промышленных каталогах.
- В качестве примера ниже приведены значения плотности некоторых твердых материалов:[6]
- алюминий = 2700 кг/м3;
- сливочное масло = 870 кг/м3;
- свинец = 11,350 кг/м3;
- прессованная древесина = 190 кг/м3.
-

2
При необходимости переведите полученный результат в другие единицы измерения. Единицы измерения при вычислении объема должны соответствовать тем, в которых приведена плотность. В противном случае необходимо перевести все в одни единицы измерения.
- Во всех примерах в предыдущем разделе объем измерялся в кубических сантиметрах. В то же время плотность некоторых материалов приведена в килограммах на кубический метр. Поскольку в одном метре содержится 100 сантиметров, кубический метр соответствует 106 кубическим сантиметрам. Поделите приведенные значения плотности на 106, чтобы найти плотность в кг/см3. Для простоты можно просто переместить десятичную запятую на 6 знаков влево.
- Четыре приведенных выше материала будут иметь следующую плотность:
- алюминий = 2700 кг/м3 = 0,0027 кг/см3;
- сливочное масло = 870 кг/м3 = 0,00087 кг/см3;
- свинец = 11,350 кг/м3 = 0,01135 кг/см3;
- прессованная древесина = 190 кг/м3 = 0,00019 кг/см3.
-

3
Чтобы найти массу, умножьте объем на плотность. Вспомните, что формула для плотности имеет следующий вид:
. Перепишем формулу так, чтобы по ней можно было найти массу:
.[7]
Реклама
-

1
Внимательно прочитайте условие задачи. При решении задач на вычисление массы необходимо до конца прочитать условие. При этом обращайте особое внимание на то, что дано. Внимательно прочитайте условие и определите, что необходимо найти. В качестве примера рассмотрим следующую задачу:
- Дан большой латунный шар диаметром 1,2 метра. Найдите массу шара.
-

2
Определите, что известно. Внимательно прочитайте условие задачи. В данном примере известен диаметр, поэтому следует использовать следующую формулу:
- Кроме того, в условии указано, что шар сделан из меди. Найдите таблицу плотностей в интернете и определите по ней плотность латуни.
- Например, с помощью сайта EngineeringToolbox.com (на английском языке) можно определить, что плотность латуни составляет 8480 кг/м3 (также можете воспользоваться сайтом www.fxyz.ru). Поскольку диаметр шара дан в метрах, для плотности необходимо использовать килограммы на кубический метр, поэтому нет необходимости переводить ее в другие единицы измерения.
-

3
-

4
Реклама
Советы
- В данной статье предполагается, что плотность однородна по всему объему шара. В большинстве математических и физических задач это условие выполняется. Однако бывает и так, что середина и внешние слои шара имеют различную плотность.
Реклама
Об этой статье
Эту страницу просматривали 49 589 раз.
Была ли эта статья полезной?
как найти массу шара зная диаметр и плотность материала?
Знаток
(474),
на голосовании
6 лет назад
Голосование за лучший ответ
Monte Kristo
Мастер
(1032)
12 лет назад
Зная диаметр шара, находим его объём (V- объём, D- диаметр) , V=(D^3)*Pi/6.
Формула определения массы такая (m- масса, d- плотность ): m=V*d.
И ещё, нужно соблюдать единицы измерения, я точно не помню, но по моему диаметр нужно считать в метрах, объём в метрах кубических, плотность в килограмм/метр кубический, и массу (по моему) в килограммах. (в единицах измерения не подскажу, так как не силён).
Как найти массу шара
Масса тела – физическая величина, которая характеризует степень его инертности. Масса физического тела зависит от объема пространства, которое оно занимает, и плотности материала, из которого оно состоит. Объем тела правильной формы (например, шара) рассчитать не сложно, а если известен и материал, из которого он состоит, то найти массу можно очень просто.

Инструкция
Определите объем шара. Для этого достаточно знать один из его параметров – радиус, диаметр, площадь поверхности и т.д. Например, зная диаметр шара (d), его объем (V) можно определить, как одну шестую часть от произведения возведенного в куб диаметра на число Пи: V=π∗d³/6. Через радиус шара (r) объем выражается как одна треть от увеличенного в четыре раза произведения числа Пи на радиус, возведенный в куб: V=4∗π∗r³/3.
Рассчитайте массу шара (m), умножив его объем на известную плотность вещества (p): m=p∗V. Если материал шара не однороден, то следует брать среднюю плотность. Подставив в эту формулу определения объема шара через его известные параметры, можно получить при известном диаметре шара формулу m=p∗π∗d³/6, а при известном радиусе m=p∗4∗π∗r³/3.
Используйте для расчетов, например, стандартный программный калькулятор, входящий в состав базового программного обеспечения операционной системы Windows любой из активно использующихся сегодня версий. Самый простой способ запустить его – нажать сочетание клавиш win + r, чтобы открыть стандартный диалог запуска программ, затем набрать команду calc и щелкнуть по кнопке «OK». В меню калькулятора раскройте раздел «Вид» и выберите строку «Инженерный» или «Научный» (в зависимости от используемой версии ОС) – интерфейс этого режима имеет кнопку для ввода значения числа Пи одним щелчком мыши. Операции умножения и деления в этом калькуляторы не должны вызвать вопросов, а для возведения в степень при вычислении массы шара будет достаточно кнопок с символами x^2 и x^3.
Источники:
- объём шара через диаметр
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем  , умноженный на плотность его материала
, умноженный на плотность его материала  (см. таблицы плотностей):
(см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой  обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
 Объем параллелепипеда:
Объем параллелепипеда:  , где
, где  — длина,
— длина,  — ширина,
— ширина,  — высота.
— высота.
Тогда масса:

2. Масса цилиндра
 Объем цилиндра:
Объем цилиндра:  , где
, где  — диаметр основания,
— диаметр основания,  — высота цилиндра.
— высота цилиндра.
Тогда масса:

3. Масса шара
 Объем шара:
Объем шара:  , где
, где  — диаметр шара.
— диаметр шара.
Тогда масса:

4. Масса сегмента шара
 Объем сегмента шара:
Объем сегмента шара:  , где
, где  — диаметр основания сегмента,
— диаметр основания сегмента,  — высота сегмента.
— высота сегмента.
Тогда масса:

5. Масса конуса
 Объем любого конуса:
Объем любого конуса:  , где
, где  — площадь основания,
— площадь основания,  — высота конуса.
— высота конуса.
Для круглого конуса:  , где
, где  — диаметр основания,
— диаметр основания,  — высота конуса.
— высота конуса.
Масса круглого конуса:

6. Масса усеченного конуса
 Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями  и
и  :
:  , где
, где  ,
,  . После никому не интересных алгебраических преобразований получаем:
. После никому не интересных алгебраических преобразований получаем:
 , где
, где  — диаметр большего основания,
— диаметр большего основания,  — диаметр меньшего основания,
— диаметр меньшего основания,  — высота усеченного конуса.
— высота усеченного конуса.
Отсюда масса:

7. Масса пирамиды
 Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)):
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)):  , где
, где  — площадь основания,
— площадь основания,  — высота пирамиды.
— высота пирамиды.
Для пирамиды с прямоугольным основанием:  , где
, где  — ширина,
— ширина,  — длина,
— длина,  — высота пирамиды.
— высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды
 Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями  и
и  :
:  , где
, где  ,
,  .
.
Исчеркав половину тетрадного листа, получаем:  , где
, где  ,
,  — ширина и длина большего основания,
— ширина и длина большего основания,  ,
,  — ширина и длина меньшего основания,
— ширина и длина меньшего основания,  — высота пирамиды.
— высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим:  .
.
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием ( ,
,  ) формула выглядит проще:
) формула выглядит проще:


Некоторые приложения тройного интеграла
Объем тела
Объем области  выражается формулой
выражается формулой 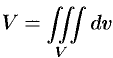 или
или
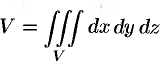 — в декартовых координатах,
— в декартовых координатах,
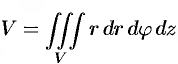 — в цилиндрических координатах,
— в цилиндрических координатах,
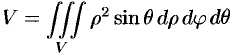 — в сферических координатах.
— в сферических координатах.
Масса тела
Масса тела 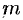 при заданной объемной плотности
при заданной объемной плотности 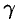 вычисляется с помощью тройного интеграла как
вычисляется с помощью тройного интеграла как
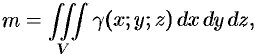
где 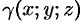 — объемная плотность распределения массы в точке
— объемная плотность распределения массы в точке 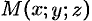 .
.
Статические моменты
Моменты 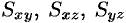 тела относительно координатных плоскостей
тела относительно координатных плоскостей 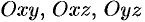 вычисляются по формулам
вычисляются по формулам
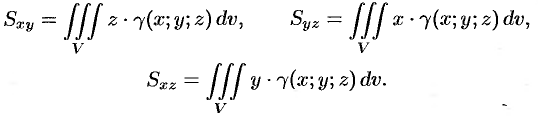
Центр тяжести тела
Координаты центра тяжести тела  находятся по формулам
находятся по формулам
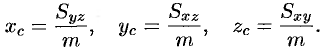
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
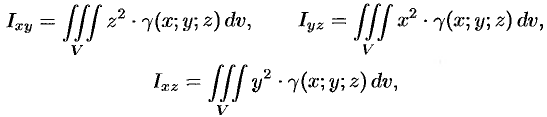
а моменты инерции относительно координатных осей:
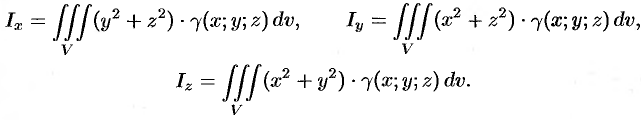
Пример №54.4.
Найти объем тела, ограниченного поверхностями 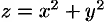 и
и 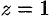 .
.
Решение:
Данное тело ограничено сверху плоскостью 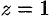 , снизу — параболоидом
, снизу — параболоидом 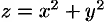 (см. рис. 231). Объем тела находим, используя цилиндрические координаты:
(см. рис. 231). Объем тела находим, используя цилиндрические координаты:
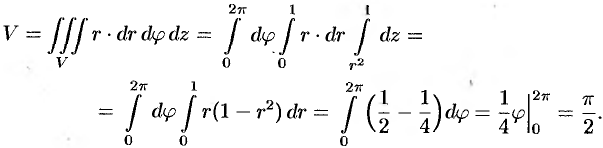
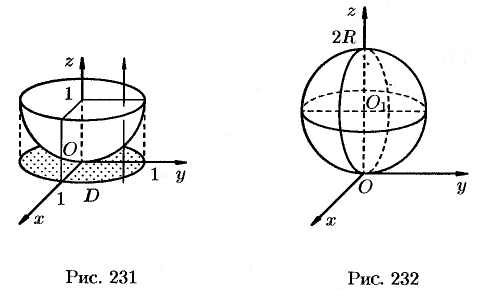
Пример №54.5.
Найти массу шара 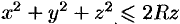 , если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение:
Уравнение сферы 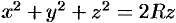 можно записать так:
можно записать так: 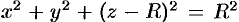 . Центр шара расположен в точке
. Центр шара расположен в точке 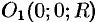 (см. рис. 232). Пусть
(см. рис. 232). Пусть 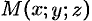 — произвольная точка шара. Тогда, по условию, плотность
— произвольная точка шара. Тогда, по условию, плотность  определяется формулой
определяется формулой
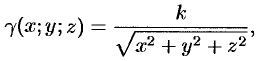
где 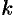 — коэффициент пропорциональности,
— коэффициент пропорциональности, 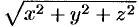 — расстояние от точки
— расстояние от точки  до начала координат.
до начала координат.
Итак, 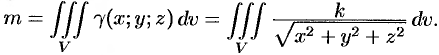
Вычислять интеграл будем в сферических координатах. Уравнение сферы 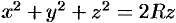 примет вид
примет вид  , т. е.
, т. е. 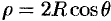 .
.
Поэтому сферические координаты будут изменяться в следующих пределах: 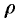 — от 0 до
— от 0 до 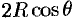 ;
; 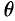 — от 0 до
— от 0 до 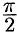 ;
; 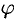 — от 0 до
— от 0 до 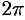 . Подынтегральная функция примет вид
. Подынтегральная функция примет вид 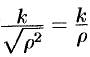 . Поэтому
. Поэтому
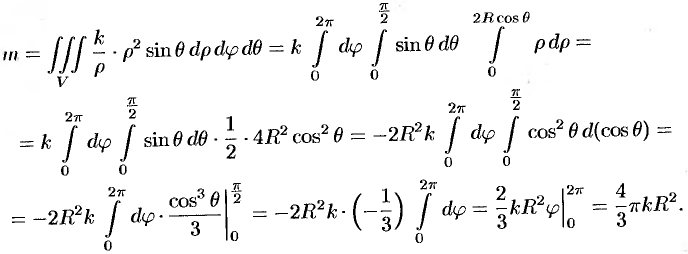
Из соображений симметрии следует, что 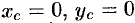 ; вычислив интеграл
; вычислив интеграл 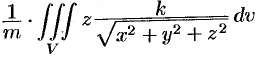 , найдем
, найдем 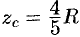 . Итак, координаты центра тяжести
. Итак, координаты центра тяжести 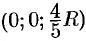 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:


