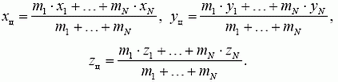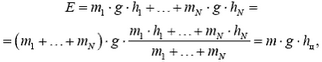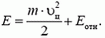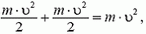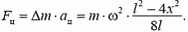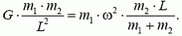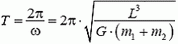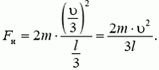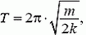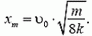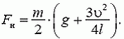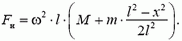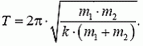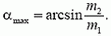В предыдущих статьях мы видели как найти массу с ускорением и силой и без ускорения и силы. Итак, в этом посте мы рассмотрим, как рассчитать массу по силе и скорости, используя несколько подходов и задач.
Существуют различные подходы к нахождению массы, но второй закон Ньютона самый простой. Это поможет вам найти массу, используя силу и скорость. Более того, формула центростремительной силы, теорема работы-энергии и кинематические уравнения движения также помогают нам найти массу, используя силу и скорость.
Масса, сила и скорость – это слова физики, которые мы также используем в нашей повседневной жизни, и они каким-то образом взаимосвязаны.
Сила – это не что иное, как физический эффект, вызывающий изменение состояния движения объекта или тела. Масса, фундаментальное свойство любого физического тела, говорит нам, сколько вещества содержится в этом конкретном теле. Фактически, он ведет себя как сопротивление, оказываемое телом, когда оно вынуждено изменить свое состояние с точки зрения движения или положения. Когда объект или тело меняют свое положение со временем под действием силы, это измерение относится к скорости объекта.
Рассмотрим каждый метод вычисление массы с помощью силы и скорость один за другим.
Как рассчитать массу по силе и скорости, используя Второй закон Ньютона:
Второй закон Ньютона можно выразить по-разному. В утверждении говорится, что когда сила действует на возражающую частицу, эта сила равна изменение импульса со временем. Следующее уравнение можно использовать для выражения этого утверждения:
Здесь буква p может использоваться для обозначения импульса объекта или частицы. Однако мы знаем, что это произведение массы и скорости объекта. В результате это записывается математически как:
р = мв
Когда мы подставляем указанное выше уравнение количества движения в уравнение силы, мы получаем следующее:
Теперь масса увеличивается только тогда, когда скорость объекта достигает скорости света. Однако здесь дело обстоит иначе. Поскольку скорость частицы или объекта не очень высока, то есть близка к скорости света, масса объекта остается постоянной. В результате мы предполагаем, что со временем изменяется только скорость, а не масса. В результате приведенное выше уравнение можно представить в виде:
………. (1)
Или,
F = ma ………. (2)
Таким образом, с точки зрения силы и скорости масса объекта может быть рассчитана следующим образом:
………. (3)
Таким образом, из уравнения (3), если мы знаем силу, действующую на тело, и то, как скорость изменяется со временем, легко вычислить массу, используя второй закон Ньютона.
Проблема: при приложении силы 25 Н скорость объекта изменяется на 5 м / с каждую секунду. Какой была бы масса объекта?
Данный:
Сила, действующая на объект F = 25 Н
Изменение скорости dv = 5 м / с
Изменение во времени dt = 1 с
Найти:
Масса объекта m =?
Решение:
Масса объекта:
∴ м = 5 кг
Таким образом, применяя силу 25 Н на объект массой 5 кг, его скорость меняется на 5 м / с каждую секунду.
Как рассчитать массу по силе и скорости с использованием центростремительной силы:
Когда тело движется по изогнутой траектории, на него действует центростремительная сила, имеющая направление внутрь, или, можно сказать, к центру.. Центростремительная сила, действующая на тело, движущееся по круговой траектории радиуса R, определяется выражением:
………. (4)
Таким образом, масса объекта, движущегося по круговой траектории, определяется как:
………. (5)
Здесь Fc используется для центростремительной силы.
Так может быть измерена масса объекта, движущегося по круговой траектории. cрассчитано с использованием центростремительная сила, скорость и радиус пути.
Проблема: Под действием центростремительной силы 3 Н шар, прикрепленный к концу струны, вращается по горизонтальной окружности с угловой скоростью 5 рад / с.-1. Какая масса у мяча, если длина шнура 60 см?
Данный:
Центростремительная сила Fc = 3 Н
Угловая скорость ⍵ = 5 рад / с
Длина шнура (радиус шнура) r = 60 см = 0.6 м.
Найти:
Масса шара m =?
Решение:
Прежде чем найти массу шара, мы находим скорость.
Скорость в терминах угловых скорость определяется выражением:
v = ⍵r
∴ v = 5 Х 0.6
∴ v = 3 м / с
Таким образом, масса мяча:
∴ м = 0.2 кг = 200 г
Таким образом, масса мяча составляет 200 граммов.
Как рассчитать массу по силе и скорости, используя Третье кинематическое уравнение движения:
Ниже приводится третье кинематическое уравнение движения:
v2 = ты2 + 2ad ………. (6)
Он показывает соотношение между начальной и конечной скоростью. Теперь мы можем применить Второй закон Ньютона (уравнение (2)) к этому уравнению и получить:
v2 = ты2 + 2 (Ф / м) д
v2 – ты2 = 2 (Ф / м) d ………. (7)
Таким образом, используя третье кинематическое уравнение, массу объекта можно рассчитать следующим образом:
………. (8)
Если вы знаете расстояние (d), которое проходит объект, когда его скорость v отличается от его начальной скорости u в результате действия силы F. В этом случае мы можем использовать третье кинематическое уравнение движения для вычисления его массы.
Проблема: предположим, что объект движется со скоростью 3 м / с. Когда к объекту прилагается сила 20 Н, он перемещается на 5 м со скоростью 7 м / с. Определить массу объекта.
Данный:
Начальная скорость объекта u = 3 м / с
Конечная скорость объекта v = 7 м / с
Сила, приложенная к объекту F = 20 Н
Расстояние, пройденное объектом под действием силы d = 5 м
Найти:
Масса объекта m =?
Решение:
Масса объекта:
∴ м = 5 кг
Таким образом, масса объекта составляет 5 кг.
Как рассчитать массу по силе и скорости, используя теорему об энергии работы:
Когда к объекту прикладывается сила, он перемещается на определенное расстояние. В результате, согласно теореме об энергии работы, работа, совершаемая объектом для перемещения на это расстояние, равна кинетической энергии, полученной объектом. Одним словом, работа превращается в энергию. Выражаясь математически:
W = KE ………. (9)
Однако работа, проделанная с объектом для перемещения на расстояние d, выглядит следующим образом:
W = F ᐧ d ………. (10)
А кинетическая энергия объекта со скоростью v равна:
………. (11)
Из уравнений (9), (10) и (11):
………. (12)
Таким образом, используя теорему об энергии работы, масса объекта определяется как:
………. (13)
Таким образом, мы можем утверждать, что нахождение массы из теоремы о работе энергии является частным случаем нахождения массы из третьего кинематического уравнения, где начальное значение объекта скорость равна нулю, подразумевая, что изначально считается, что он находится в состоянии покоя.
Проблема: предположим, что коробка лежит на горизонтальной поверхности. При толкании с силой 60 Н он скользит по поверхности на 15 м со скоростью 30 м / с. Определите массу объекта.
Данный:
Усилие, приложенное к коробке F = 60 Н
Расстояние, пройденное коробкой под действием силы d = 15 м.
Скорость объекта на этом расстоянии v = 30 м / с
Найти:
Масса ящика m =?
Решение:
Масса ящика:
∴ м = 2 кг
Таким образом, масса ящика 2 кг.
Как найти массу, зная скорость
Умение определять массу движущегося тела может пригодиться не только на школьных уроках физики, но и в обычной жизни. Предположим, требуется поднять экскаватором автомобиль, масса которого неизвестна, при этом известна скорость, с которой машина будет поднята.
Инструкция
Воспользуйтесь формулой F=ma, где F – сила (измеряется в ньютонах), m – масса автомобиля, a – ускорение. Чтобы найти массу, примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Получится: m=F/a.
Теперь замените ускорение известной величиной – скоростью (V). Воспользуйтесь формулой a=V/t, где t – время, за которое поднимется машина. Если время дано в секундах, а скорость в метрах в минуту, то уравняйте величины. Переведите либо время в минуты, либо скорость в метры с секунду.
В исходную формулу m=F/a подставьте полученное значение ускорения. Получится: m=F/V/t. Воспользуйтесь правилом деления на дробь: «При делении на обычную дробь ее знаменатель уходит наверх, а числитель – вниз». Отсюда: m=Ft/V.
Теперь, чтобы найти массу, подставьте в формулу m=Ft/V известные значения. Например: F=50 Н (ньютонов), t=10 с (секунд), V=1 м/c (метров в секунду). Получится: m=50 Н х 10 с / 1 м/с, m=500 килограммов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Страйкбол » Расчет скорости, массы и энергии шара
Расчет скорости, массы и энергии шара
В страйкболе жесткие ограничения начальной скорости вылета шара из ствола и его энергии (в джоулях).
Калькулятор дульной энергии
Чтобы не нарушить правила, вы можете воспользоваться онлайн-калькулятором (хронографом) расчета скорости и энергии шара:
Таблица соотношения скорости выстрела, массы шара и его энергии
По таблице вы можете определить, как соотносится масса шара с начальной скоростью выстрела и энергией.
Начальную скорость вылета принято измерять шаром с массой 0.2 грамма. Однако не всегда такие шары есть под рукой и иногда замеры проводятся шарами другого веса. Данная таблица поможет вам пересчитать начальную скорость шара массой 0.2 грамма, независимо от того, какую массу шара использовали при замерах на хронометре.
Выписки из нормативно-правовых актов
Закон РФ «Об оружии» в ред. от 29.06.2004 N 58-ФЗ «Правилами оборота гражданского и служебного оружия и патронов к нему на территории Российской Федерации.
Приобретение, транспортирование и использование спортивного пневматического оружия калибра 6 мм и 8 мм с дульной энергией менее 7,5 Дж осуществляется свободно, без получения лицензий/разрешений органов внутренних дел, но при энергии более 3 Дж оно не может быть автоматическим и содержать в магазине более 10 патронов.
Выдержка из Правил страйкбола (версия СК) о допуске пневматического оружия до игр.
4.1. Игровое стрелковое оружие, обозначенное в Правилах, должно стрелять промышленно изготовленными, однородными, с содержанием пластиковой смеси и отсутствием ярко выраженного содержания металла, шариками ВВ калибра 6 мм или 8 мм весом от 0,12 до 0,48 грамма включительно.
4.2. Дульная энергия игрового стрелкового оружия определяется как:
Дульная энергия = Масса шара (кг) *скорость вылета шара из ствола в квадрате (м/с*м/с)/2.
4.2.1. Для расчета дульной энергии игрового оружия специальной аппаратурой измеряется скорость вылета шара из ствола.
4.2.2. Процедура замера дульной энергии:
- магазин замеряемого игрового стрелкового оружия заряжается шарами заданной известной массы;
- производится два одиночных выстрела в воздух;
- производится три одиночных выстрела через измерительную аппаратуру. Фактическим значением дульной энергии принимается наибольшее из показанных значений;
- Для ВВД винтовок – на инлайн регулятор наносится пломба, исключающая изменение его настроек. При наличии – активируются другие блокировки изменения настроек системы.
*Отстрел производится с дистанции не менее 15 см от первой пары датчиков измерительного прибора.
4.3. Для применения в зданиях допускается:
Любое игровое стрелковое оружие с дульной энергией при замере шаром массы 0,2 гр. не более 1,4 Дж (со скоростью шара на выходе из ствола не более 120 м/с.)
Выписка из правил страйкбола (приказ министра спорта Российской Федерации).
Определяющим фактором при допуске привода к соревнованиям является энергия вылета шара.
К соревнованиям допускаются приводы с энергией вылета шара не более 1,56 Дж (соответствует скорости вылета шара весом 0,2 г не более 125 м/с).
В зависимости от региона, ограничения по применяемому оружию в зданиях могут отличаться.
Черноуцан А. Задачи на центр масс // Квант. — 1996. — № 2. — С. 43-45.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении механических задач неоценимую помощь может оказать использование понятия центра масс системы материальных точек. Одни задачи просто невозможно решить, не прибегая к этому понятию, решение других с его помощью может стать гораздо проще и нагляднее.
Перед тем как обсуждать конкретные задачи, напомним основные свойства центра масс и проиллюстрируем их примерами.
Центром масс (центром инерции) системы материальных точек назовем точку, характеризующую распределение масс в системе, координаты которой определяются формулами
Здесь mi — массы материальных точек, образующих систему, xi, yi, zi — координаты этих точек. Читатели, знакомые с понятием радиуса-вектора, предпочтут векторную запись:
(1)
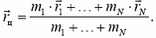
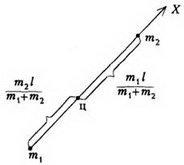
Пример 1. Найдем положение центра масс, простейшей системы, состоящей из двух точек, массы которых m1 и m2 и расстояние между ними l (рис. 1).
Рис. 1
Направив ось X от первой точки ко второй, получим, что расстояние от первой точки до центра масс (т.е. координата центра масс) равно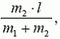 
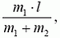
а расстояние от центра масс до второй точки равно 
т.е. отношение расстояний обратно отношению масс. Значит, в этом случае положение центра масс совпадает с центром тяжести.
Обсудим некоторые свойства центра масс, что, как нам кажется, наполнит физическим содержанием приведенное выше несколько формальное определение этого понятия.
1) Положение центра масс не изменится, если какую-то часть системы заменить одной точкой с массой, равной массе этой подсистемы, и находящейся в ее центре масс.
Пример 2. Рассмотрим плоский однородный треугольник и найдем положение его центра масс. Разделим треугольник на тонкие полоски, параллельные одной из сторон, и заменим каждую полоску точкой, расположенной в ее середине. Так как все такие точки лежат на медиане треугольника, центр масс тоже должен лежать на медиане. Повторяя рассуждения для каждой из сторон, получаем, что центр масс находится на пересечении медиан.
2) Скорость центра масс можно найти, взяв производную по времени от обеих частей равенства (1):
(2)
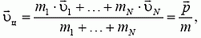
где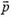 
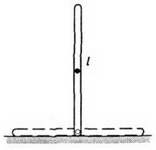
— импульс системы, m — полная масса системы. Видно, что скорость центра масс замкнутой системы постоянна. Значит, если связать с центром масс поступательно движущуюся систему отсчета, то она будет инерциальной.
Пример 3. Поставим однородный стержень длиной l вертикально на гладкую плоскость (рис. 2) и отпустим. В процессе падения как горизонтальная составляющая его импульса, так и горизонтальная составляющая скорости центра масс будут оставаться равными нулю. Поэтому в момент падения центр стержня окажется в том месте, где первоначально стоял стержень, а концы стержня сместятся по горизонтали на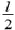 
.
Рис. 2
3) Ускорение центра масс равно производной от его скорости по времени:
(3)
где в правой части равенства стоят только внешние силы, так как все внутренние силы сокращаются по третьему закону Ньютона. Получаем, что центр масс, движется так, как двигалась бы воображаемая точка с массой, равной массе системы, под действием результирующей внешней силы. Наверное, это самое физическое свойство центра масс.
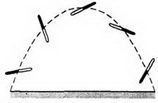
Пример 4. Если бросить палку, приведя ее при этом во вращение, то центр масс палки (ее середина) будет двигаться с постоянным ускорением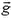 
по параболе (рис. 3).
Рис. 3
4) Пусть система точек находится в однородном поле тяжести. Тогда суммарный момент сил тяжести относительно любой оси, проходящей через центр масс, равен нулю. Это значит, что равнодействующая сил тяжести проходит через центр масс, т.е. центр масс является также центром тяжести.
5) Потенциальная энергия системы точек в однородном поле тяжести вычисляется по формуле
где hц — высота центра масс системы.
Пример 5. При выкапывании в однородном фунте ямы глубиной h и разбрасывании грунта по поверхности его потенциальная энергия возрастает на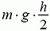 
, где m — масса извлеченного грунта.
6) И еще одно полезное свойство центра масс. Кинетическая энергия системы точек может быть представлена в виде суммы двух слагаемых: кинетической энергии общего поступательного движения системы, равной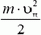 
, и кинетической энергии Eотн движения относительно системы отсчета, связанной с центром масс:
Пример 6. Кинетическая энергия обруча, катящегося без проскальзывания по горизонтальной поверхности со скоростью υ, равна
так как относительное движение в этом случае представляет собой чистое вращение, для которого линейная скорость точек обруча равна υ (полная скорость нижней точки должна быть равна нулю).
Теперь приступим к разбору задач на использование центра масс.
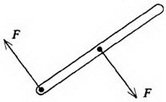
Задача 1. Однородный стержень лежит на гладкой горизонтальной поверхности. К стержню прикладывают две одинаковые по величине, но противоположные по направлению горизонтальные силы: одна сила приложена к середине стержня, другая — к его концу (рис. 4). Относительно какой точки начнет поворачиваться стержень?
Рис. 4
На первый взгляд может показаться, что осью вращения будет точка, лежащая посередине между точками приложения сил. Однако уравнение (3) показывает, что поскольку сумма внешних сил равна нулю, то равно нулю и ускорение центра масс. Значит, центр стержня будет оставаться в покое, т.е. служить осью вращения.
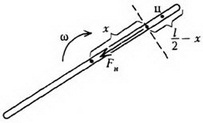
Задача 2. Тонкий однородный стержень длиной l и массой m привели в движение вдоль гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите, натяжение стержня в зависимости от расстояния x до его центра.
Перейдем в инерциальную систему отсчета, связанную с центром стержня. Рассмотрим движение куска стержня, заключенного между рассматриваемой точкой стержня (расположенной на расстоянии x от центра) и его концом (рис. 5).
Рис. 5
Единственной внешней силой для этого куска является искомая сила натяжения Fн, масса равна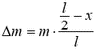 
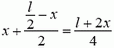
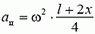
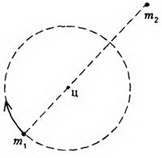
, а его центр масс движется по окружности радиусом 
с ускорением 
. Записывая уравнение движения центра масс выделенного куска, получим
Задача 3. Двойная звезда состоит из двух звезд-компонентов массами m1 и m2, расстояние между которыми не меняется и остается равным L. Найдите период вращения двойной звезды.
Рассмотрим движение звезд-компонентов в инерциальной системе отсчета, связанной с центром масс двойной звезды. В этой системе отсчета звезды движутся с одной и той же угловой скоростью по окружностям разных радиусов (рис. 6).
Рис. 6
Радиус вращения звезды массой m1 равен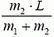 
(см. Пример 1), а ее центростремительное ускорение создается силой притяжения к другой звезде:
Видим, что период вращения двойной звезды равен
и определяется полной массой двойной звезды, независимо от того, как она распределена между звездами-компонентами.
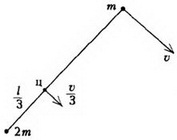
Задача 4. Две точечные массы m и 2m связаны невесомой нитью длиной l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорость массы 2m равна нулю, а скорость массы m равна υ и направлена перпендикулярно нити (рис. 7). Найдите натяжение нити и период вращения системы.
Рис. 7
Центр масс системы находится на расстоянии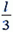 
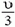
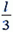
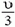
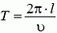
от массы 2m и движется со скоростью 
. В системе отсчета, связанной с центром масс, точка массой 2m движется по окружности радиусом со скоростью . Значит, период вращения равен 
(проверьте, что такой же ответ получается, если рассмотреть точку массой m). Натяжение нити найдем из уравнения движения любой из двух точек:
Задача 5. На гладкой горизонтальной плоскости лежат два одинаковых бруска массой m каждый, связанных легкой пружиной жесткостью k (рис. 8). Первому бруску сообщают скорость υ0 в направлении от второго бруска. Опишите движение системы. Через какое время деформация пружины впервые достигнет максимального значения?
Рис. 8
Центр масс системы будет перемещаться с постоянной скоростью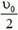 
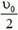
. В системе отсчета центра масс начальная скорость каждого бруска равна , а жесткость половинной пружины, которая соединяет его с неподвижным центром масс, составляет 2k (жесткость пружины обратно пропорциональна ее длине). Период таких колебаний равен
а амплитуда колебаний каждого бруска, которую можно найти из закона сохранения энергии, составляет
В первый раз деформация станет максимальной через четверть периода, т.е. через время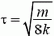 
.
Задача 6. Шар массой m налетает со скоростью υ на покоящийся шар массой 2m. Найдите скорости обоих шаров после упругого центрального удара.
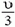
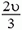
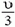
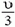
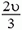
В системе отсчета, связанной с центром масс, полный импульс двух шаров равен нулю как до, так и после coyдарения. Легко догадаться, какой ответ для конечных скоростей удовлетворяет одновременно и этому условию, и закону сохранения энергии: скорости останутся такими же, как до удара, по величине, но изменят свои направления на противоположные. Скорость центра масс системы равна . В системе центра масс первый шар движется со скоростью 
, а второй шар движется навстречу первому со скоростью . После удара шары будут разлетаться с такими же скоростями. Осталось вернуться в первоначальную систему отсчета. Применяя закон сложения скоростей, находим, что конечная скорость шара массой m равна и направлена назад, а скорость покоившегося раньше шара массой 2m равна и направлена вперед.
Отметим, что в системе центра масс очевидным является утверждение, что при ударе относительная скорость шаров не меняется по величине, но меняется по направлению. А так как разность скоростей при переходе в другую инерциальную систему отсчета не изменяется, можно считать, что мы вывели это важное соотношение и для первоначальной системы отсчета:
υ1 – υ2 = u1 – u2,
где буква υ используется для обозначения начальных скоростей, а u — для конечных. Это уравнение можно решать совместно с законом сохранения импульса вместо закона сохранения энергии (куда скорости входят во второй степени).
Задача 7. Известно, что при упругом нецентральном ударе двух одинаковых шаров, один из которых до удара покоился, угол разлета равен 90°. Докажите это утверждение.
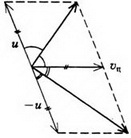
В системе центра масс нецентральный удар можно описать следующим образом. До удара шары сближаются с одинаковыми импульсами, после удара они разлетаются с такими же по величине, но противоположно направленными импульсами, а прямая разлета поворачивается на некоторый угол относительно прямой сближения. Чтобы перейти обратно в начальную систему отсчета, надо каждую конечную скорость сложить (векторно!) со скоростью центра масс. В случае одинаковых шаров скорость центра масс равна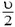 
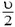
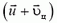
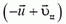
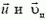
, где υ — скорость налетающего шара, и в системе отсчета центра масс шары сближаются и разлетаются с одинаковыми скоростями . В том, что после сложения каждой конечной скорости со скоростью центра масс получаются взаимно перпендикулярные векторы, можно убедиться из рисунка 9. А можно и просто проверить, что скалярное произведение векторов 
и 
обращается в ноль в силу того, что модули векторов 
равны друг другу.
Рис. 9
Упражнения
1. Стержень массой m и длиной l шарнирно закреплен за один из концов. Стержень отклонили на некоторый угол от вертикального положения и отпустили. В момент прохождения вертикального положения скорость нижней точки равна υ. Найдите натяжение в средней точке стержня в этот момент времени.
2. Стержень массой m и длиной l вращают в горизонтальной плоскости с угловой скоростью ω вокруг одного из его концов. Найдите зависимость натяжения стержня от расстояния x до оси вращения, если на другом конце закреплен маленький грузик массой М.
3. Найдите период колебаний для системы, описанной в задаче 5 статьи, но для брусков различных масс m1 и m2.
4. Выведите известные общие формулы для упругого центрального удара двух шаров, используя переход в систему отсчета центра масс.
5. Шар массой m1 налетает на покоящийся шар меньшей массы m2. Найдите максимально возможный угол отклонения налетающего шара при упругом нецентральном ударе.
Ответы
1. 
2. 
3. 
5. 
Главная 
Учёба 
Калькулятор расчётов массы, скорости, кинетической энергии
Калькулятор расчётов массы, скорости, кинетической энергии
Условные обозначения формулы: m – масса тела, V – скорость, E – кинетическая энергия.
Формула расчёта кинетической энергии: E=m*V2/2. Масса тела, умноженная на скорость в квадрате и разделённая на два.
Формула расчёта массы : m=E/V2*2. Кинетическая энергия, разделённая на скорость в квадрате и умноженное на два.
Формула расчёта скорости: V=[квадратный корень][E/(1/2*m)]. Кинетическую энергию, делим на половину массы и извлекаем квадратный корень.
Заполните поля, оставив, пустым, только поле которое вы хотите узнать. Например: чтобы узнать кинетическую энергию, заполните массу и скорость.
Калькулятор расчёта массы, скорости, кинетической энергии, онлайн
Потенциальная энергия тела
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
