Маленький шарик массой m с зарядом q = 5 нКл, подвешенный к потолку на лёгкой шёлковой нитке длиной l = 0,8 м, находится в горизонтальном однородном электростатическом поле E с модулем напряжённости поля E = 6 ⋅ 10⁵ В/м. Шарик отпускают с нулевой начальной скоростью из положения, в котором нить вертикальна. В момент, когда нить образует с вертикалью угол α = 30°, модуль скорости шарика v = 0,9 м/с. Чему равна масса шарика m ? Сопротивлением воздуха пренебречь.
Решение:
Как и разбор любой другой задачи, начнем с рисунка, где постараемся отметить все важные данные для данной абстрактной задачи:
Заметим, что если начать решать эту задачу со второго закона Ньютона, то не получится найти ничего полезного в силу того, что мы не знаем тангенциального ускорения, а при проекции на ось, параллельную нити, у нас будет оставаться неизвестная сила натяжения нити T:
Поэтому попробуем решить задачу из энергетического подхода. Выберем нулевой уровень потенциальной энергии там, где находился бы шарик при свободном висе на веревке, а также при отсутствии электрического поля. По условию задачи сказано, что шарик отпускают с нулевой скоростью из положения, когда нить вертикальна. Значит у нас в этой точке и потенциальная и кинетическая энергия равны нулю. Далее шарик разгоняется за счет силы Лоренца со стороны электрического поля. Работа сил электрического поля тратится на увеличение потенциальной энергии и на увеличение кинетической энергии. В момент, когда нить образует с вертикалью угол α = 30°, шарик имеет заданную скорость, а также находится на некоторой высоте h = L⋅(1 – cosα). Итак, запишем энергию до и после включения поля. Найдем изменение полной механической энергии от включения до того момента, когда шарик достигнет угла α = 30°.
Теперь определим работу силы Лоренца (силы со стороны электрического поля). В силу того, что данное поле является потенциальным, то работа не зависит от пути, а зависит только от начального и конечного положения, которые мы соединим вектором перемещения S.
Геометрия задачи даст нам следующие соотношения:
Работа поля получится такой:
Записав закон изменения энергии, получим уравнение, которое будет линейно относительно массы груза. Из него и находим массу шарика:
Понравился разбор задачи? Проявите активность: лайк, репост, комментарий.
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Изучение колебаний груза на нити»
 Лабораторная работа 1
Лабораторная работа 1
«Изучение колебаний груза на нити»
Цель: изучение зависимости характеристик математического маятника от амплитуды колебаний, массы груза, длины нити.
Оборудование: два математических маятника с подвесами (шариками различной массы), штатив с зажимом, линейка, секундомер, весы, разновес.
Ход работы
1. Найдите массу шарика первого маятника путем взвешивания: m1=200г =0.2 кг.
2. Измерьте длину маятника (от точки подвеса до центра шарика). Длина должна быть не менее 1м. l1= 40 см = 0.4м.
3. Изучите зависимость периода колебаний маятника от амплитуды его колебаний
Таблица 1.
| № | l1, м | m1, кг | N | 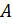 , м , м
|
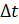 , с , с
|
T, c | Tсредн, c |
|
0.4 |
0.2 |
0.1 |
1.268 |
1.268 |
|||
| 1.268 | |||||||
| 1.268 | |||||||
|
0.2 |
1.268 |
1.268 |
|||||
| 1.268 | |||||||
| 1.268 | |||||||
|
0.3 |
1.268 |
1.268 |
|||||
| 1.268 | |||||||
| 1.268 |
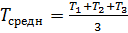
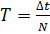
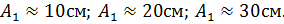
4.Исходя из формулы период малых колебаний маятника не зависит от амплитуды его колебаний ( Ответ на 4)
 По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от амплитуды его колебаний.
По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от амплитуды его колебаний.
5. Найдите массу шарика второго маятника путем взвешивания: m2= 100 г = 0.1 кг.
Таблица 2.
| № | l1, м | m2, кг | N | 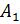 , м , м
|
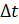 , с , с
|
T, c | Tсредн, c |
|
0.4 |
0.1 |
0.1 |
1.268 |
1.268 |
|||
| 1.268 | |||||||
| 1.268 |
 6. Сравните полученное значение периода колебаний с полученным в таблице 1. По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от массы шарика.
6. Сравните полученное значение периода колебаний с полученным в таблице 1. По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от массы шарика.
Исходя из формулы периода малых колебаний мятника не зависит от массы шарика
7. Измените длину маятника: сначала l2=75см и затем l3=50см. Повторите измерение периода колебаний, оставив неизменными массу m2 шарика и амплитуду 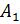 его колебаний.
его колебаний.
Таблица 3.
| № | l, м | m2, кг | N | 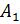 , м , м
|
 , с , с
|
T, c | Tсредн, c |
|
0.75 |
0.1 |
0.1 |
1.736 |
1.736 |
|||
| 1.736 | |||||||
| 1 .736 | |||||||
|
0.5 |
1.418 |
1.418 |
|||||
| 1.418 | |||||||
| 1.418 |
8. По результатам измерений и вычислений сделайте вывод, зависит ли период колебаний маятника от его длины.
Период колеб. маятника зависит от 2 его длины
Контрольные вопросы:
1) Какую длину имеет математический маятник, период колебаний которого π секунд?

T=2π√(L/g) L=gT²/4π²
2)Как изменится период колебаний маятника, если массу шарика уменьшить в 3 раза, а длину нити маятника увеличить в 3 раза?

Масса не влияет ,а при увеличении длины в 3 раза ,период увеличивается в 3 раза
 Выводы:
Выводы:
Мы научились: изучение зависимости характеристик математического маятника от амплитуды колебаний, массы груза, длины нити
Суперзадание.Изготовьте математический маятник длиной 1 м. Экспериментально определите период его колебаний. Результат проанализируйте и сделайте вывод.
2014-06-01 ![]()
К маятнику АВ с шариком массой $M$ подвешен маятник ВС с шариком массой $m$ (рис.). Точка А совершает колебания в горизонтальном направлении с периодом $T$. Найти длину нити ВС, если известно, что нить АВ все время остается вертикальной.

Решение:

Поскольку нить АВ остается вертикальной, на шарик массы $M$ во время движения системы не действуют горизонтальные силы. Это означает, что горизонтальные силы не действуют и на систему, состоящую из двух шариков $M$ и $m$, и шарики должны двигаться так, чтобы их центр масс не перемещался в горизонтальном направлении (рис.). Поэтому шарик массы $m$ движется так, как будто он прикреплен к нити длины $x$ (где $x$ – расстояние от шарика до центра масс системы). Период колебаний такого маятника
$T=2 pi sqrt{x/g}$. (1)
Этот период, очевидно, равен периоду колебаний точки А.
Найдем теперь $x$. По свойству центра масс
$xm=(l-x)M$.
Отсюда
$x=l frac{M}{m+M}$. (2)
Подставляя это выражение для $x$ в формулу (1), получим:
$T= 2 pi sqrt{frac{l}{g} cdot frac{M}{m+M}}$.
Отсюда
$l=frac{T^{2}g}{4 pi^{2}} frac{m+M}{M}$
Длина нити математического маятника l, масса шарика m. Определите силу, действующую на шарик, при отклонениях его от положения равновесия на x в случае, если
Как зависит от x потенциальная энергия шарика?
Спрятать решение
Решение.
Сила, вызывающая колебания
В проекции на оси:
Для случая
Тогда сила, действующая на шарик, равна:
Для малых углов отклонения колебания являются гармоническими, то есть сила пропорциональна смещению значит, коэффициент пропорциональности
Тогда потенциальная энергия шарика
Ответ:
Источник: Савченко О. Я. Задачи по физике, М.: «Наука», 1988 (№ 3.1.5)
Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
