|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 5 |
|
|
1 |
|
Масса шкива10.02.2017, 23:02. Показов 3275. Ответов 8
Приветствую. Подскажите, пожалуйста, какой максимальной массы шкив можно установить на вал электродвигателя по ссылке ?: http://electronpo.ru/dvigatel_air80b Спасибо. Добавлено через 11 часов 54 минуты Двигатель закреплен на станине. На длину вала установлен шкив. Шкив ни с чем не соединён и вращается. Какой максимальной массы шкив возможно установить? Спасибо.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
10.02.2017, 23:02 |
|
8 |
|
362 / 345 / 74 Регистрация: 18.03.2015 Сообщений: 1,288 |
|
|
11.02.2017, 10:52 |
2 |
|
Не вижу смысла считать “отвлеченные” массы. Шкив внешним диаметром 100 мм и шкив внешним диаметром 1000 мм и той же массой будут вести себя по разному.
1 |
|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 5 |
|
|
11.02.2017, 16:00 [ТС] |
3 |
|
да – момент инерции у них разный при вращении – соответственно больший диаметр будет оказывать большее воздействие на вал. Спасибо.
0 |
|
3371 / 1895 / 570 Регистрация: 09.04.2015 Сообщений: 5,312 |
|
|
13.02.2017, 09:27 |
4 |
|
при вращении какой массы двигатель сломается Что значит “сломается”
Не вижу смысла считать “отвлеченные” массы. Вы совсем слабо описываете задачу, сводя ее к примитиву.
1 |
|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 5 |
|
|
13.02.2017, 17:27 [ТС] |
5 |
|
Попробую по другому сформулировать. У двигателя в целом как механизма есть предел допустимых нагрузок, которые конструктивно в нём заложены и допускают его эксплуатацию. Спасибо.
0 |
|
Модератор
8802 / 6585 / 894 Регистрация: 14.02.2011 Сообщений: 23,147 |
|
|
13.02.2017, 17:41 |
6 |
|
Применительно к массе и диаметру шкива при просто вращении с валом двигателя какие есть ограничения для шкива это называется момент на валу, должен быть указан в паспорте, меряется в кг на см или Ньютон на метр
1 |
|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 5 |
|
|
13.02.2017, 17:46 [ТС] |
7 |
|
Как этот момент с характеристиками шкива связать ? Спасибо.
0 |
|
Модератор
8802 / 6585 / 894 Регистрация: 14.02.2011 Сообщений: 23,147 |
|
|
13.02.2017, 17:51 |
8 |
|
Как этот момент с характеристиками шкива связать ? массу умножить на радиус
1 |
|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 5 |
|
|
13.02.2017, 17:56 [ТС] |
9 |
|
а обороты вала двигателя должны учитываться? Спасибо.
0 |
Unit Converter
Enter the mass of the object being lifted and the number of ropes between pulley sets into the calculator to determine the effort force or weight of the pulley.
- Belt Length Calculator (2 pulley system)
- AMA (Actual Mechanical Advantage) Calculator
- Mechanical Advantage Calculator (Lever)
- Belt Speed Calculator
- Pulley Torque Calculator
- Pulley System Velocity Ratio Calculator
- Pulley Force Calculator
- Pulley Efficiency Calculator
Pulley Weight Formula
The following formula is used to calculate the weight or effort force of a pulley system.
- Where eF is the effort force
- m is the mass of the object
- g is the acceleration due to gravity
- u is the friction factor of the system (=1 for ideal systems
- n is the number of ropes between the pulley sets of pulleys
To calculate the pulley weight effort, multiply the mass by the acceleration from gravity, then divide by the product of the friction factor times the number of ropes between pulley sets.
Pulley Weight Definition
Pulley weight is defined as the weight or effort force seen by the end of a pulley system when lifting an object of set mass at a constant speed.
Pulley Weight Example
How to calculate a pulley weight?
First, determine the mass of the object being lifted. For this example, the object being lifted is 20 kg.
Next, determine the friction factor for the system. In short, this is the mechanical efficiency of the system. For a system with no friction at all this would be equal to 1. For this problem, we will assume the factor is .8.
Next, determine the number of ropes in between the pulleys. This is the number of ropes not including the end ropes being pulled and directly attached to the object.
For this problem, we are looking at a pulley system of 4 pulleys with 4 ropes in between.
Finally, calculate the pulley weight/effort force using the formula.
eF = (20*9.81)/(.8*4) = 61.3125 N

При решении задачи
Д8 необходимо использовать теорию и
примеры решения задач Д4 и Д7.
Пример Д8.
Механическая система состоит из
ступенчатого шкива 2 (радиусы ступеней
R2
и r2),
груза 1 и сплошного катка 3,
прикрепленных к концам нитей, намотанных
на ступени шкива (рис. Д8).
На шкив
при его
|
Рис.
|
вращении действует Дано:
R2
P3
Определить: |
Решение.
1. Система состоит из груза 1, шкива 2,
катка 3 и нитей; система имеет одну
степень свободы. Выберем в качестве
обобщенной координаты координату х1
груза 1, полагая, что груз движется вниз,
и отсчитывая х1
в сторону движения;
![]() ;
;
обобщенная скорость
![]()
или
![]() .
.
Уравнение Лагранжа, с учетом выбранной
обобщенной координаты и соответствующей
обобщенной скорости, имеет вид
![]()
(1)
2. Определим
кинетическую энергию Т
системы, равную сумме кинетических
энергий всех тел (вычисления здесь
аналогичны вычислениям, проводившимся
в задаче Д4):
![]()
(2)
Так как груз 1
движется поступательно, шкив 2 вращается
вокруг неподвижной оси, а каток 3 совершает
плоскопараллельное движение, то
![]()
![]() .
.
(3)
Поскольку масса
шкива считается распределенной по
внешнему ободу, а каток – сплошной (его
радиус обозначим r3),
то
![]()
(4)
3. Все скорости,
входящие в T1,
T2
и T3
(2,
3,
![]() ),
),
выразим через обобщенную скорость
![]() .
.
Из рис.
Д8 следует,
что
![]() ,
,
то есть
![]() ,
,
(5)
а также
![]() ,
,
откуда, с учетом (5), получаем
![]() .
.
(6)
Точка K
– мгновенный центр скоростей катка,
следовательно,
![]() ;
;
подставляя (6), находим
![]() .
.
(7)
Подставляя (4)-(7) в
(3), а затем значения T1,
T2,
T3
в (2), получаем
 ,
,
или
![]() .
.
(8)
4. Вычислим
производные, входящие в (1), учитывая
(8):
![]() ,
,
так как T
не зависит от x1
; (9)
![]() .
.
(10)
5. Найдем обобщенную
силу Q.
Активные силы, действующие на систему:
![]() ,
,
![]() ,
,
![]()
и момент сил сопротивления М2,
направленный против вращения шкива.
Сообщим системе возможное перемещение,
при котором обобщенная координата х1
получает положительное приращение
![]() ,
,
и покажем перемещения каждого из тел;
для груза 1 это будет
![]() ,
,
для шкива 2 – поворот на угол
![]() ,
,
для катка 3
– перемещение
![]()
его центра. Эти перемещения указаны на
рис. Д8. После этого вычислим сумму
элементарных работ сил и момента на
данных перемещениях; получим
![]()
(11)
Сила
![]()
работы не совершает, так как приложена
к точке неподвижной оси.
Все входящие в
(11) перемещения надо выразить через
![]() .
.
Учитывая, что зависимости между
элементарными перемещениями аналогичны
зависимостям (5), (6) между соответствующими
скоростями, получим
![]() ,
,
(12)
![]() .
.
(13)
Подставляя (12),
(13) в (11) и вынося
![]()
за скобки, найдем
![]()
Коэффициент
при
![]()
в полученном выражении и будет обобщенной
силой Q.
Следовательно,
![]() ,
,
(14)
или
![]()
(15)
6.
Подставляя найденные величины (9), (10) и
(15) в уравнение (1), получим
![]()
Отсюда находим
искомое ускорение
![]() .
.
Ответ: а1
= 0,37g.
Примечание1.
Если в ответе получится а
< 0 (или ε <
0), то это означает, что система движется
не в ту сторону, куда было предположено.
Тогда у момента М2,
направленного против вращения шкива,
изменится направление и, следовательно,
как видно из равенства (14), изменится
величина Q,
для которой надо найти новое верное
значение.
Примечание 2.
Если требуется найти закон изменения
обобщенной координаты (закон движения
груза 1), то, учитывая, что
![]() ,
,
интегрируем это уравнение и находим
![]() .
.
128
Соседние файлы в папке Теоретическая механика
- #
- #
- #
- #
- #
- #
Решение.
Покажем рисунок.
Момент сил которые действуют на маховик определим по формуле:
М = J∙ε (1), М = FН∙R (2).
J – момент инерции маховика, ε – угловое ускорение движения маховика, FН – сила натяжения нити, R – радиус шкива.
Определим угловое ускорение движения шкива. Груз из состояния покоя движется равноускоренно.
[ a=frac{2cdot s}{{{t}^{2}}} (3), varepsilon =frac{a}{R}, varepsilon =frac{2cdot s}{Rcdot {{t}^{2}}} (4). ]
Используя второй закон Ньютона определим силу натяжения нити.
[ begin{align}
& vec{F}=mcdot vec{a}, {{{vec{F}}}_{H}}+mcdot vec{g}=mcdot vec{a}, \
& Ox: -{{F}_{H}}+mcdot g=mcdot a, {{F}_{H}}=mcdot g-mcdot a, {{F}_{H}}=mcdot (g-frac{2cdot s}{{{t}^{2}}}) (5). \
end{align} ]
(5) подставим в (2), (4) подставим в (1) (2) подставим в (1) выразим момент инерции маховика.
[ J=frac{{{R}^{2}}cdot mcdot (g-frac{2cdot s}{{{t}^{2}}})cdot {{t}^{2}}}{2cdot s} (6). ]
J = 0,024 кг∙м2.
| 🎓 Заказ №: 21911 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
На горизонтальную ось насажены маховик и легкий шкив радиусом 5 см. На шкив намотан шнур, к которому привязан груз массой 0,4 кг. Опускаясь равноускоренно, груз прошел путь 1,8 м за время 3 с. Определить момент инерции маховика. Массу шкива считать пренебрежимо малой.
Решение Система движущихся тел в данной задаче включает в себя вращающийся вокруг своей оси маховик и груз массой m1 , движущийся поступательно. На груз действуют две силы: сила тяжести m g 1 и сила натяжения нити T . На маховик действуют сила тяжести mg , сила реакции опоры N и сила натяжения нити T . Сила тяжести и сила реакции опоры проходят через ось вращения маховика и, следовательно, момент этих сил относительно этой оси равен нулю. Вращение цилиндра обусловлено силой натяжения нити T . Момент этой силы относительно оси вращения равен M TR (1) Где R – радиус маховика. Запишем основное уравнение вращательного движения для цилиндра: I M (2)

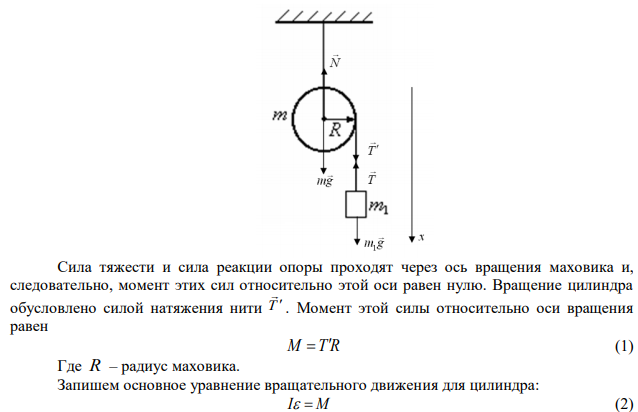
Готовые задачи по физике которые сегодня купили:
- На платформе, движущейся со скоростью 3 м/с, укреплено орудие, ствол которого направлен в сторону движения и составляет с горизонтом угол 60.
- Два моля водяного пара находятся в объеме 2 л.
- Давление газа в 3 раза больше критического значения, молярный объем газа в 2 раза больше критического значения.
- Найти среднюю длину свободного пробега молекул азота при условии, что его динамическая вязкость η = 17 мкПа·с.
- Вал массой 50 кг и радиусом 10 см вращается с частотой 8 об/с.
- В результате некоторого процесса вязкость идеального газа увеличилась в α = 2,0 раза, а коэффициент диффузии – в β =4,0 раза.
- Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины
- Аргон в количестве 2 моль изотермически расширяется от объема 2 л до объема 4 л.
- В соленоиде без сердечника длиной l , содержащем N витков, величина тока изменяется во времени по закону I=at+bt
- Найти приращение энтропии 10 моль углекислого газа при изотермическом расширении от объема 1 л до объема 2 л.




