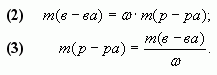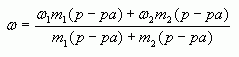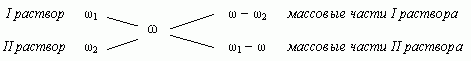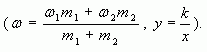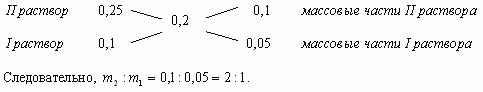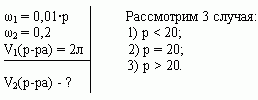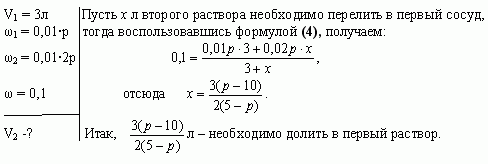“Только из союза двоих, работающих
вместе и при помощи друг друга, рождаются великие
вещи.”
Антуан Де Сент-Экзюпери
Математика многообразна и многогранна.
Существует ряд ситуаций в образовательном
процессе, когда при изучении какой-либо темы по
физике, химии, биологии и т.д. затрагиваются
понятия математики, например, существуют задачи,
которые решают как на уроках математики, так и на
уроках химии. Способы решения задач представляют
и учителя химии, и математики, но есть проблема:
математики знают математику, а химики – химию. И
не всегда способы совпадают.
В данной статье приводятся рекомендации по
решению химических задач на смешение растворов
разными способами: с помощью расчетной формулы,
“Правила смешения”, “Правила креста”,
графического метода, алгебраического метода.
Приведены примеры решения задач.
1. Основные химические понятия
Приведем некоторые указания к решению задач на
растворы.
Основными компонентами этого типа задач
являются:
а) массовая доля растворенного вещества в
растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются
однородными;
б) смешивание различных растворов происходит
мгновенно;
в) объем смеси равен сумме объемов смешиваемых
растворов;
г) объемы растворов и массы сплавов не могут
быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в
растворе – это отношение массы этого вещества к
массе раствора.
где – массовая
доля растворенного вещества в растворе;
– масса
растворенного вещества в растворе;
– масса
раствора.
Следствия формулы (1):
Введем обозначения:
– массовая доля
растворенного вещества в первом растворе;
–
массовая доля растворенного вещества во втором
растворе;
–
массовая доля растворенного вещества в новом
растворе, полученном при смешивании первого и
второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) – массы
растворенных веществ в соответствующих
растворах;
m1(р-ра), m2(р-ра), m(р-ра) – массы
соответствующих растворов.
Основными методами решения задач на смешивание
растворов являются: с помощью расчетной формулы,
“Правило смешения”, “Правило креста”,
графический метод, алгебраический метод.
Приведем описание указанных методов.
1.1. С помощью расчетной формулы
В наших обозначениях, получим формулу для
вычисления массовой доли вещества (?) в смеси.
1. Масса полученного при смешивании раствора
равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в
первом и втором растворах:
m1(в-ва)= •m1(р-ра), m2(в-ва)=
•m2(р-ра).
3. Следовательно, масса растворенного вещества
в полученном растворе вычисляется как сумма масс
веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = •m1(р-ра) +
•m2(р-ра).
4. Таким образом, массовая доля растворенного
вещества в полученном растворе равна:
или
или
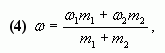
где – массы
соответствующих растворов.
Замечание: При решении задач удобно
составлять следующую таблицу.
|
1-й раствор |
2-й раствор |
Смесь двух растворов |
|
|
Масса растворов |
m1 |
m2 |
m1 + m2 |
|
Массовая доля |
|
|
|
|
Масса вещества в |
|
|
|
1.2. “Правило смешения”
Воспользуемся формулой (4):
тогда 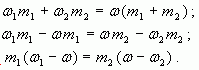
Отсюда
Таким образом, отношение массы первого
раствора к массе второго равно отношению
разности массовых долей смеси и второго раствора
к разности массовых долей первого раствора и
смеси.
Аналогично получаем, что при
Замечание: Формула (5) удобна тем, что на
практике, как правило, массы веществ не
отвешиваются, а берутся в определенном
отношении.
1.3. “Правило креста”
“Правилом креста” называют диагональную
схему правила смешения для случаев с двумя
растворами.
Слева на концах отрезков записывают исходные
массовые доли растворов (обычно слева
вверху-большая), на пересечении отрезков –
заданная, а справа на их концах записываются
разности между исходными и заданной массовыми
долями. Получаемые массовые части показывают в
каком отношении надо слить исходные растворы.
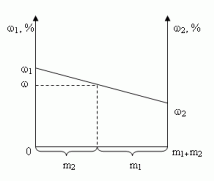
1.4. Графический метод
Отрезок прямой (основание графика)
представляет собой массу смеси, а на осях ординат
откладывают точки, соответствующие массовым
долям растворенного вещества в исходных
растворах. Соединив прямой точки на осях ординат,
получают прямую, которая отображает
функциональную зависимость массовой доли
растворенного вещества в смеси от массы
смешанных растворов в обратной пропорциональной
зависимости
Полученная функциональная прямая позволяет
решать задачи по определению массы смешанных
растворов и обратные, по массе смешанных
растворов находить массовую долю полученной
смеси.
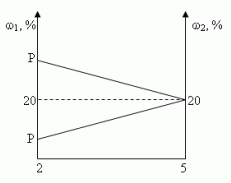
Построим график зависимости массовой доли
растворенного вещества от массы смешанных
растворов. На одной из осей ординат откладывают
точку, соответствующую массовой доли , а на другой –
. Обозначим на оси абсцисс
точки А и В с координатами (0,0) и (m1 + m2,0),
соответственно. На графике точка А(0,0)
показывает, что массовая доля всего раствора
равна , а точка В(m1
+ m2,0) – массовая доля всего раствора равна . В направлении от
точки А к точке В возрастает содержание в
смеси 2-го раствора от 0 до m1+ m2 и
убывает содержание 1-го раствора от m1+ m2
до 0. Таким образом, любая точка на отрезке АВ будет
представлять собой смесь, имеющую одну и ту же
массу с определенным содержанием каждого
раствора, которое влияет на массовую долю
растворенного вещества в смеси.
Замечание: Данный способ является наглядным
и дает приближенное решение. При использовании
миллиметровой бумаги можно получить достаточно
точный ответ.
1.5. Алгебраический метод
Задачи на смешивание растворов решают с
помощью составления уравнения или системы
уравнений.
2. Примеры решения задач
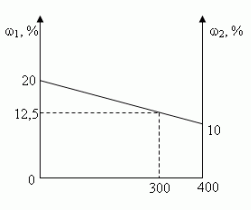
Задача 1. (№1.43, [1])
В 100 г 20%-ного раствора соли добавили 300 г её
10%-ного раствора. Определите процентную
концентрацию раствора.
Решение:
- C помощью расчетной формулы
- Графический
- Путем последовательных вычислений
- Сколько растворенного вещества содержится:
- Сколько вещества содержится в образовавшемся
растворе? - Чему равна масса образовавшегося раствора?
- Какова процентная концентрация полученного
раствора? - Алгебраический
Ответ: 12,5%
а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]
б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]
20 г + 30 г = 50 г
100 г + 300 г = 400 г
(50/400)100 = 12,5(%)
Ответ: 12,5%
Пусть х – процентная концентрация
полученного раствора. В первом растворе
содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в
полученном растворе х•(100 + 300)(г) соли.
Составим уравнение:
0,2•100 + 0,1•300 = х•(100 + 300);
х = 0,125 (12,5%)
Ответ: 12,5%
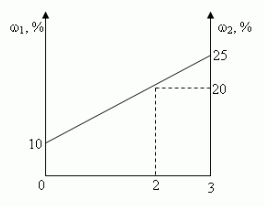
Задача 2. u(№10.26, [1])
Смешали 10%-ный и 25%-ный растворы соли и получили 3
кг 20%-ного раствора. Какое количество каждого
раствора в килограммах было использовано?
Решение:
- Алгебраический
- Графический.
- “Правило смешения”
- “Правило креста”
а) C помощью уравнения:
Пусть х (кг) – масса 1-го раствора, тогда 3-х (кг)
-масса 2-го раствора.
0,1•х (кг) содержится соли в 1-ом растворе,
0,25•(3-х) (кг) содержится соли в 2-ом растворе,
0,2•3 (кг) содержится соли в смеси.
Учитывая, что масса соли в 1-ом и 2-ом растворах
равна массе соли в смеси, составим и решим
уравнение:
0,1•х + 0,25•(3-х) = 0,2•3;
0,15х = 0,15;
х = 1, 1кг-масса 1-го раствора
3 – х = 3 – 1 =2 (кг) – масса 2-го раствора.
Ответ: 1 кг, 2 кг.
б) С помощью системы уравнений
Пусть х (кг) – количество первого раствора, у (кг)
– количество второго раствора. Система уравнений
имеет вид:
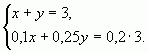
Ответ: 1 кг, 2 кг.
Ответ: 1кг, 2кг.

Составим диагональную схему
Ответ: 1кг, 2кг.
Задача 3 ([2])
Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму)
раствора соли. Сколько литров 20%-ного раствора
такой же соли надо налить в сосуд, чтобы
процентное содержание соли в сосуде стало
наибольшим?
Решение (графический способ)
Заметим, что по условию, объём второго раствора
не превышает трёх литров.
- Ели р < 20, то для того, чтобы получить
максимальную массовую долю вещества в растворе,
необходимо добавить 3 л 20% – ного раствора соли; - Если р = 20, то при добавлении 2-го раствора,
процентное содержание соли в растворе не
изменится, следовательно, можно прилить от 0 л до 3
л 20% – ного раствора соли; - Если р > 20, то при добавлении 2-го раствора,
процентное содержание соли будет уменьшаться,
т.е. прилить нужно 0 л.
Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20
< р 100.
Задача 4 (работа 5, №2, [1])
В двух сосудах по 5л каждый содержится раствор
соли. Первый сосуд содержит 3л р% – ного раствора, а
второй – 4л 2р% – ного раствора одной и той же соли.
Сколько литров надо перелить из второго сосуда в
первый, чтобы получить в нем 10% – ный раствор соли?
При каких значениях р задача имеет решение?
Решение
Найдем, при каких значениях р задача имеет
решение. По условию задачи 5-ти литровый сосуд
содержит 3л первого раствора, следовательно, к
нему можно прилить от 0 до 2л второго раствора.
Имеем, Решая
неравенство, получаем
Ответ:
3. Заключение
Данные рекомендации предназначены учителям
математики, желающим организовать элективные
курсы, как в девятых, так и в десятых и
одиннадцатых классах. Цель создаваемых курсов:
научить учащихся пользоваться математическим
аппаратом при решении химических задач.
Список литературы
- Галицкий и др. Сборник задач по алгебре для 8-9
классов: Учебное пособие для учащихся шк. и
классов с углубл. изуч. математики / М.Л. Галицкий,
А.М. Гольдман, Л.И. Звавич.-2-е изд. – М.:
Просвещение,1994. – 271с. - Сборник задач по математике для поступающих в
вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С.
Иванов и др.; Под ред. А.И. Прилепко. – М.:Высш. школа,
1983. – 239 с. - Ерыгин Д.П., Шишкин Е.А. Методика решения задач по
химии: Учебное пособие для студентов пед. ин-тов
по биол. и хим. спец. – М.: Просвещение,1989. – 176с. - Хомченко Г.П., Хомченко И.Г. Задачи по химии для
поступающих в вузы: Учебное пособие. – 2-е изд..
исправ. и доп. – М.: Высш. школа, 1993. – 302 с.
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
При смешивании масса полученного
раствора (m) равняется сумме масс
смешиваемых растворов (m1, m2,
m3 … mn):
m = m1 + m2 + m3 +…+ mn,
г
Аналогично, масса растворенного вещества
будет равна сумме масс веществ в
смешиваемых растворах:
m(X) = m1(X) + m2(X) + m3(X) +…+
mn(X), г
Пример 12. Определить массовую долю
HNO3 в растворе, полученном при
смешивании 100 мл раствора с ω1(HNO3)
= 10% (ρ1 = 1,05 г/мл) и 150 мл раствора с
ω2(HNO3) = 20% (ρ2 = 1,12
г/мл).
Решение:
ω(HNO3) =
=
Находим
m1(р-ра) = V1(р-ра)·ρ1(р-ра)
= 100·1,05 = 105 г
m2(р-ра) = V2(р-ра)·ρ2(р-ра)
= 150·1,12 = 168 г
m1(HNO3) = m1(р-ра)·ω1(р-ра)
= 105·0,1 = 10,5 г
m2(HNO3) = m2(р-ра)·ω2(р-ра)
= 168·0,2 = 33,6 г
Рассчитываем
ω(HNO3) =
= 0,162 или 16,2%
Ответ: массовая доля HNO3 в
растворе после смешения равна 0,162 или
16,2%.
Пример 13. Какие объемы растворов
гидроксида калия с ω1(KOH) = 50%
(ρ1 = 1,51 г/мл) и с
ω2(KOH) = 10% (ρ2 = 1,1 г/мл)
необходимо использовать для приготовления
одного литра раствора гидроксида калия
с ω(KOH) = 20% (ρ = 1,19 г/мл)?
Решение:
Масса полученного раствора равна
m(р-ра) = m1(р-ра) + m2(р-ра)
m(р-ра) = V(р-ра)·ρ(р-ра) = 1000·1,19 = 1190 г
Отсюда m1(р-ра) = 1190 – m2(р-ра)
Масса KOH в полученном растворе равна
m(KOH) = m(р-ра)·ω(KOH) = 1190·0,2 = 238 г
В то же время масса КОН в полученном
раствора равна:
m(KOH) = m1(KOH) + m2(KOH)
m1(KOH) = m1(р-ра)·ω1(KOH) =
m1(р-ра)·0,5
m2(KOH) = m2(р-ра)·ω2(KOH) =
m2(р-ра)·0,1
Получаем 238 = m1(р-ра)·0,5 + m2(р-ра)·0,1
Подставим в это уравнение выражение
для m1(р-ра):
238 = [1190 – m2(р-ра)]·0,5 + m2(р-ра)·0,1
Решим уравнение относительно m2(р-ра):
0,4m2(р-ра) = 357 m2(р-ра) = 892,5 г
Тогда m1(р-ра) = 1190 – 892,5 = 297,5 г
Находим объемы растворов:
V1(р-ра) =
=
=
197 мл
V2(р-ра) =
=
=
811,4 мл
Ответ: V1 = 197 мл, V2 = 811,4
мл.
1. 5. Задания для самостоятельной работы
1. Определите массовую долю
растворенного вещества (Х)% в следующих
растворах:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m(X), г |
5 |
28 |
46,7 |
53,1 |
62,2 |
|
m(H2O), г |
300 |
450 |
528 |
630 |
720 |
2. Рассчитать массу вещества (г),
необходимую для приготовления следующих
растворов:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω(Х),% |
2 |
1 |
5 |
10 |
8 |
|
Объем р-ра, л |
0,25 |
0,8 |
0,5 |
0,3 |
0,45 |
|
ρ, г/мл |
1,015 |
1,007 |
1,046 |
1,090 |
1,067 |
3. Рассчитайте массу кристаллогидрата
Х·nH2O (г) и объем воды (мл), необходимые
для приготовления 500 мл следующих
растворов:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
Вещество (Х·nH2O) |
CuSO4·5H2O |
FeSO4·7H2O |
Na2SO4·10H2O |
MgSO4·7H2O |
AlCl3·6H2O |
|
ω(соли),% |
0,25 |
6 |
15 |
0,085 |
10 |
|
ρ, г/мл |
1,06 |
1,11 |
1,13 |
1,04 |
1,02 |
4. Рассчитать массу кристаллогидрата
Х·nH2O (г), которую надо растворить
в воде для получения раствора, содержащего
Х% безводной соли:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
Вещество (Х·nH2O) |
CuSO4·5H2O |
FeSO4·7H2O |
Na2SO4·10H2O |
MgSO4·7H2O |
AlCl3·6H2O |
|
ω(Х),% |
8 |
15 |
18 |
6 |
20 |
|
Объем воды |
0,66 л |
400 мл |
0,75 л |
350 мл |
900 мл |
5. Сколько литров газа (н.у.)
необходимо растворить в V мл воды для
получения раствора с массовой долей,
указанной в таблице:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω(Х),% |
17 |
30 |
2 |
1,5 |
3 |
|
Вещество |
NH3 |
HCl |
CO2 |
SO2 |
H2S |
|
V воды, мл |
200 |
1500 |
900 |
600 |
1000 |
6. Определить объем воды, в котором
надо растворить V л газа (н.у.), для
получения раствора с указанной массовой
долей:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω(Х),% |
20 |
25 |
3 |
2 |
15 |
|
Вещество |
NH3 |
HCl |
CO2 |
SO2 |
H2S |
|
V, л |
40 |
56,5 |
3,2 |
12,5 |
1,5 |
7. Определите массу раствора (г),
который можно приготовить из воды и
щелочи KOH, если:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m(H2O), г |
100 |
150 |
175 |
225 |
250 |
|
ω(KOH),% |
15 |
20 |
25 |
30 |
35 |
8. Рассчитать массовую долю (%)
растворенных веществ, содержащихся в
V л воды:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
Вещество (Х) |
HCl |
H2S |
CO2 |
NH3 |
SO2 |
|
V(X), л |
10 |
2 |
1 |
20 |
0,5 |
|
V воды, л |
1,5 |
4,5 |
6,5 |
0,4 |
0,65 |
9. Определить массу воды (г), которую
надо добавить к указанной массе раствора
m1 с массовой долей вещества ω1(Х),
для получения раствора с массовой долей
ω2(Х):
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m1, г |
500 |
700 |
900 |
980 |
993 |
|
ω1(Х),% |
40 |
50 |
58 |
60 |
72 |
|
ω2(Х),% |
20 |
32 |
36 |
40 |
53 |
10. Определить объем воды, который
следует выпарить из исходного раствора
массой m1 с
массовой долей вещества ω1(Х),
чтобы получить раствор, в котором
массовая доля соли равна ω2(Х):
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m1, г |
200 |
250 |
300 |
350 |
400 |
|
ω1(Х),% |
10 |
20 |
30 |
40 |
50 |
|
ω2(Х),% |
25 |
42 |
50 |
60 |
80 |
11. Определить объем раствора HNO3
с указанными массовой долей ω1(HNO3)
и плотностью, который необходимо добавить
к 1,2 л воды для получения раствора с
массовой долей ω2(HNO3) = 10%:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω1(Х),% |
52 |
60 |
63 |
70 |
75 |
|
ρ1, г/мл |
1,3 |
1,35 |
1,36 |
1,40 |
1,43 |
12. Какой объем раствора CuSO4
с указанными в таблице массовой долей
ω2(CuSO4) и плотностью ρ2
можно приготовить из 120 мл раствора с
массовой долей ω1(CuSO4) = 42%
(ρ1
= 1,36 г/мл)?
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω2(CuSO4),% |
52 |
60 |
63 |
70 |
75 |
|
ρ2, г/мл |
1,3 |
1,35 |
1,36 |
1,40 |
1,43 |
13. Какие объемы растворов серной
кислоты с массовой долей ω1(H2SO4)
и плотностью ρ1 и массовой долей
ω2(H2SO4) и плотностью
ρ2 необходимо взять для приготовления
2 литров раствора H2SO4 с
массовой долей ω(H2SO4) = 14% (ρ
= 1,095 г/мл)?
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω1(H2SO4),% |
30 |
35 |
38 |
40 |
50 |
|
ρ1, г/мл |
1,219 |
1,32 |
1,35 |
1,38 |
1,4 |
|
ω2(H2SO4),% |
6 |
5 |
4,8 |
4 |
2 |
|
ρ2, г/мл |
1,038 |
1,030 |
1,028 |
1,022 |
1,018 |
14. Определить массовую долю Na2CO3
в растворе, полученном при растворении
указанной массы кристаллогидрата
Na2CO3·10Н2О в растворе
Na2CO3 массой m с массовой долей
ω1(Na2CO3) = 13%:
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m(Na2CO3·10Н2О), г |
40 |
46 |
48 |
52 |
56 |
|
m, г |
300 |
420 |
450 |
500 |
530 |
15. Какую массу раствора гидроксида
калия с массовой долей ω1(KOH) надо
добавить к раствору KOH массой m2 и
массовой долей ω2(KOH), чтобы получить
раствор KOH с массовой долей ω3(KOH)?
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
ω1(KOH),% |
20 |
30 |
40 |
50 |
60 |
|
m2, г |
1000 |
500 |
480 |
35 |
25 |
|
ω2(KOH),% |
50 |
10 |
90 |
5 |
2 |
|
ω3(KOH),% |
25 |
20 |
15 |
10 |
5 |
16. Сколько литров NH3 (н.у.)
необходимо растворить в растворе NH3·Н2О
массой m1 с массовой долей ω1(NH3)
для получения раствора NH3·Н2О
с массовой долей ω(NH3)?
|
Вариант |
|||||
|
а |
б |
в |
г |
д |
|
|
m1, г |
200 |
300 |
400 |
500 |
600 |
|
ω1(NH3),% |
10 |
12 |
15 |
18 |
20 |
|
ω(NH3),% |
15 |
18 |
20 |
25 |
33,5 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методика решения задачи на определение начальной массы смеси двух веществ при полной нейтрализации полученной смеси
Задача 1.
В воде растворили смесь оксида натрия и оксида калия, где массовая доля натрия 46%. Определите массу начальной смеси, если для полной нейтрализации полученной смеси израсходовано 175 мл 2 молярного раствора серной кислоты.
Решение:
М(Na2O ) = (2 • 23) + 16 = 62 г/моль;
М(К2O ) = (2 •39) + 16=94 г/моль.
Из формулы оксида натрия Na2O следует, что на 46 весовых частей Na приходится 16 весовых частей О, т.е. на 46% Na в смеси оксидов будет приходится 16% О. Тогда смесь оксидов натрия и калия будет содержать 62% (46 + 16 = 62) Na2O. Соответственно, содержание К2О в смеси будет 38% (100 – 61 = 100).
Уравнение реакции имеет вид:
Me2O + H2SO4 = Me2SO4 + H2O
Из уравнения реакции следует, что на нейтрализацию 1 моля оксидов натрия или калия расходуется 1 моль серной кислоты.
Рассчитаем количество серной кислоты по условию задачи, получим:
(175мл • 2моль/1000мл) = 0,35 мол. Значит, n(смеси) = 0,35 мол.
Смесь содержит 0,35 моль оксидов натрия и калия .
Обозначим массу смеси оксидов через х г.
Тогда
n(Na2O) = (62% • х г)/(100% • 62 г/моль) = 0,01х моль;
n(К2O) = (38% • х г)/(100% • 94 г/моль) = 0,0004х моль.
Теперь рассчитаем массу смеси оксидов натрия и калия, используя алгебраическое уравнение, получим:
0,01х + 0,004х = 0,35;
0,014х = 0,35;
х = 0,35/0,014 = 25 г; m((смеси) = 25 г.
Отсюда
m(Na2O) = [m((смеси) • w%( Na2O)]/100% = [(25г • 62%)]/100% = 15,5 г;
m(К2O) = [m((смеси) • w%( К2O)]/100% = [(25 г • 38%)]/100% = 9,5 г.
Ответ: m(смеси) = 2 5г.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 2»
Решение текстовых задач: задач на смеси, сплавы и растворы при подготовке к ГИА по математике.
( рекомендации учащимся)
Колбасова Л.А., учитель математики высшей категории
1. Теоретические основы решения задач на сплавы и смеси
Решение задач на смеси, сплавы, растворы требует определенной теоретической базы.
Это различные определения, такие как концентрация, процентное содержание и др., а также и всевозможные допущения, например:
1) всё, что мы рассматриваем, считается однородным;
2) все процессы происходят мгновенно;
3) полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;
4) величины, получаемые в результате вычислений, не могут быть со знаком минус.
Существует несколько способов решения задач на слияние растворов. Например, можно воспользоваться расчетной формулой, как это делают на уроках химии. Из области математики можно пользоваться графическим или же алгебраическим методами.
Задачи на смеси и сплавы бывают двух видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
Масса раствора равна сумме масс всех составляющих.
Алгоритм решения задач на смеси и сплавы:
- Определить, какое вещество влияет на концентрацию раствора (главное вещество).
- Следить за весом главного вещества при добавлении других веществ в раствор.
- Исходя из данных об изменениях состояния главного вещества – сделать выводы.
Как правило, концентрация выражается в процентах.
Процент – это сотая доля числа. Она может выражаться либо в виде десятичной дроби (0,11), либо в виде процента (11%).
Важно знать:
1.Масса раствора (смеси, сплава) равна сумме масс всех составляющих.
Если мы смешаем 3 литра апельсинового сока и 77 литров воды, то получим 10
10 литров апельсинового нектара (сделаем предположение, что смешивание происходит в автоматическом режиме, а не вручную).
2.При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Если мы смешаем 6 литров яблочного сока и 66 литров персикового сока – то получится 12 литров яблочно-персикового сока.
И еще одна очевидность (последняя).
3.Масса растворенного вещества при смешивании двух растворов суммируется.
Если мы смешаем 3 литра яблочного сока с 10% мякоти (0,3 л), и 55 литров яблочного сока с 5% мякоти (0,25 л), то получим 88 литров сока с 0,55 л мякоти
(0,3+0,25).
2. Простейшие задачи на смеси и сплавы
Задачи на смеси и сплавы бывают двух основных видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
Пример 1.
В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решение:
- Для начала вычислим, сколько кислоты содержится в 5% растворе. Из 3,8 кг 5% – это кислота, а значит в растворе 0,05 * 3,8=0,19 кг кислоты
2. Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.
3. Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – 0,19 кг. Таким образом, концентрация кислоты стала равна 0,19:5=0,038
4. Теперь выразим концентрацию в процентах – 0,038⋅100%=3,8%
Ответ: 3,8
Теперь давай попробуем решить задачу посложнее.
Пример 2.
Смешали 3 кг 5%-го водного раствора щелочи и 7 кг 15%-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.
Решение:
Давай попробуем визуализировать ситуацию. 3 кг 5% водного раствора. Значит воды в этом растворе 95%.
Нарисуем:
А теперь второй раствор:
После смешивания, вновь получившийся раствор будет весить 3кг + 7 кг = 10 кг. Обозначим количество щелочи в новом растворе за x, а количество воды – (10−x):
Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе –0,05⋅3=0,15 кг щелочи
и 3−0,15=2,85 кг воды,
во втором – 0,15⋅7=1,05 кг щелочи
и 7−1,05=5,95 кг воды:
Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: x=0,15+1,05=1,2 кг кислоты.
Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:
1,2:10=0,12
Поскольку ответ просят дать в процентах – умножим на 100%
0,12⋅100%=12%.
Ответ: 12.
Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
3. Алгебраический метод
Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или систем неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.
Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений. Главное внимание при обучении учащихся способу решения текстовых задач методом составления уравнений должно быть обращено на сознательную отработку этапности решения.
В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.
1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.
2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.
3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.
4. Изучение полученного решения, критический анализ результата.
При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.
Этапы решения задачи:
1. Знакомство с текстом задач и выделение основных компонентов в них. Заполнение таблицы.
Таблица для решения задач имеет следующий вид:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
Или в таком виде:
|
1 – й р-р |
2 – й Р-р |
Смесь 2 растворов |
|
|
Масса растворов |
|||
|
Массовая доля раств-го вещества |
|||
|
Масса вещества в растворе |
2. Составление уравнения и его решение.
3. Анализ полученных данных, ответ на вопрос задачи.
Рассмотрим примеры решения задач с помощью таблицы.
Пример 4. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?
Решение.
Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в руде) до и после удаления примесей.
|
Масса руды, кг |
Масса железа, кг |
Концентрация (доля железа в руде) |
|
|
Руда |
500 |
х |
|
|
Руда после удаления примесей |
500-200=300 |
х-0,125⋅200= x-25 |
|
Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна .
Так как масса железа в 200 кг примесей равна 0,125⋅200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна .
По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:
Найдём, что 212,5 кг – масса железа в руде. Найдём остаток железа в руде после удаления примесей: 212,5-25=187,5 (кг).
Ответ: 187,5 кг.
Пример 5. Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
|
Наим-е веществ, растворов, смесей, сплавов |
% содержание меди (доля сод-я в-ва) |
Масса раствора (смеси, сплава) |
Масса вещества |
|
Первый сплав |
15%=0,15 |
хг |
0,15х |
|
Второй раствор |
65%=0,65 |
(200 – х)г |
0,65(200–х)=130–0,65х |
|
Получившийся р-р |
30%=0,3 |
200 г |
200 |
Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы):
Решив это уравнение, получаем х=140. При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять140г, а второго 60г.
Ответ:140г. 60г.
Рассмотрим еще несколько примеров решения задач с помощью таблицы. Как правило обе части уравнения умножают на100, при этом избегают решения уравнения с десятичными дробями.
6. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
|
Количество раствора |
5 л |
+7 л |
= 12 л |
|
% содержания растворенного вещества |
12 % |
0 % |
х % |
|
Количество растворенного вещества |
|
|
|
|
5 5 х = 5 Ответ: 5. |
7. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
|
Количество раствора |
4 л |
+ 6 л |
= 10 л |
|
% содержания растворенного вещества |
15 % |
25 % |
х % |
|
4 2 х = 21 Ответ: 21. |
8. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
|
виноград |
изюм |
||
|
Количество раствора |
х кг |
20 кг |
|
|
% содержания растворенного вещества |
100 – 90 = 10 % |
100 – 5 = 95 % |
|
|
10х = 20 х = 190 Ответ: 190. |
9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
|
Количество раствора |
х кг |
+ (200 – х) кг |
= 200 кг |
|
% содержания растворенного вещества |
10 % |
30 % |
25 % |
|
10х + 30(200 – х) = 200 х + 3(200 – х) = 20 х + 600 – 3х = 500 – 2х = – 100 х = 50 (200 – 50) – 50 = 100 Ответ: 100. |
10. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
|
Количество раствора |
х кг |
+ у кг |
+ 10 кг |
= х + у + 10 |
|
% содержания растворенного вещества |
30 % |
60 % |
0 % |
36 % |
|
Количество раствора |
х кг |
+ у кг |
+ 10 кг |
= х + у + 10 |
|
% содержания растворенного вещества |
30 % |
60 % |
50 % |
41 % |
|
х=4 Ответ: 60. |
Задания для самостоятельного решения:
1. (Типовые тестовые задания ЕГЭ 2012 п/р А.Л.Семенова, И.В.Ященко). Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?
2. Первый раствор содержит 40% кислоты, а второй – 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 % раствора, то получился бы 70 % раствор. Сколько литров 60 % раствора кислоты было первоначально?
Список использованной литературы.
1. Кузнецова Л.В. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. – М.: Просвещение, 2010.
2. Прокопенко Н.И. Задачи на смеси и сплавы.- М. :Чистые пруды, 2010 (Библиотечка «Первого сентября». Выпуск 31 )
3. Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.
4. Малахова Н. А., Орлов В. В. и др. Методика работы с сюжетными задачами: Учебно-методич. пособие. СПб.: Изд-во РГПУ, 1992. 46 с.
5. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989
6. www.mathege.ru
7. www.fipi.ru
8. www. festival.1september.ru
9. http://www.shevkin.ru/
10. http://mat-ege.ru