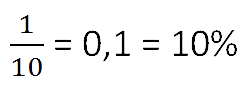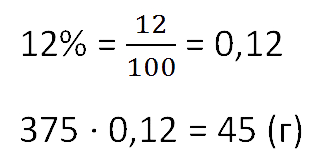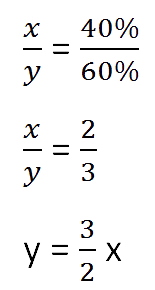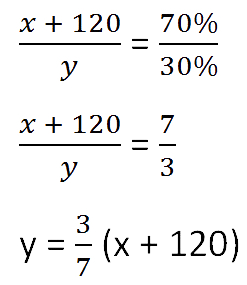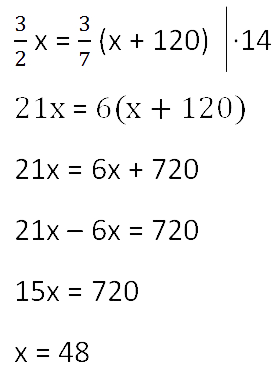Чему равна масса раствора соли 19-процентного (в граммах), в котором содержится 95 грамм соли?
Решение задачи
Для решения задачи используем формулу нахождения массовой доли растворенного вещества:
выразим массу раствора соли:
Найдем массу раствора соли:
m (раствора) = 95 /0,19 = 500 (г).
Если раствор 19-процентный, то массовая доля соли в нем 0,19.
Ответ:
масса раствора соли 500 грамм.
Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.
Запомните!
Концентрация раствора — это часть, которую составляет масса растворённого вещества от
массы всего раствора.
- 9%-я концентрация раствора соли — это 9 грамм соли в
100 граммах раствора.
Разбор примера
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
- 1 кг — масса растворённого вещества (соли)
- 9 кг — масса воды в растворе (не путать с общей массой раствора)
- 9 + 1 = 10 кг — общая масса раствора.
Ответ: 10% — концентрация раствора.
Разбор примера
Теперь решим обратную задачу.
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.
Ответ: 45 г соли.
Сложная задача на растворы
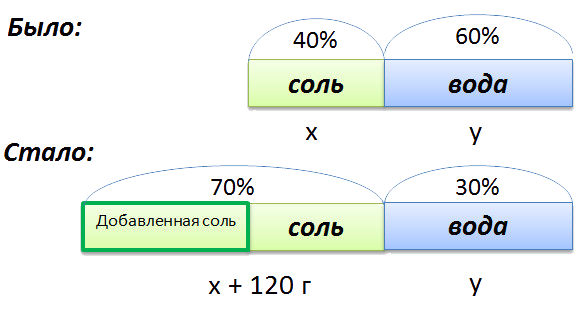
В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% − 40%= 60%
Изобразим графически условия задачи.
Составим пропорцию, связывающую эти величины до добавления соли.
Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.
Этой величиной является масса воды в растворе «y».
Выразим её, учитывая изменения в растворе после добавления соли.
- (x + 120) г — масса соли в новом растворе
- (100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.
Ответ: 48 г — масса соли в первоначальном растворе.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
31 октября 2016 в 18:30
Роман Роршахов
Профиль
Благодарили: 0
Сообщений: 1
Роман Роршахов
Профиль
Благодарили: 0
Сообщений: 1
Сколько граммов 6%-ного раствора соли можно получить из 300 г жидкости содержащей 40% этой соли?
0
Спасибо
Ответить
5 ноября 2016 в 21:36
Ответ для Роман Роршахов
София Деревянко
Профиль
Благодарили: 0
Сообщений: 2
София Деревянко
Профиль
Благодарили: 0
Сообщений: 2
Если соли 40%, то воды — 60%. проценты характеризуют массовые доли, значит в растворе 120 г соли. Для нахождения массы раствора составляем пропорцию, которую можно прочитать так ЕСЛИ 120 Г СОЛИ СОСТАВЛЯЕТ 6 % ОТ ВСЕГО РАСТВОРА, ТО ВЕСЬ РАСТВОР (100%) БУДЕТ ВЕСИТЬ Х г, 120: 6=Х: 100, отсюда находим Х=120: 6 · 100, вес всего раствора 2 кг. проверяем, 2000 г · 0,06 получается 120г. Количество соли не изменилось))))
0
Спасибо
Ответить
6 сентября 2015 в 12:03
Дарья Сидорова
Профиль
Благодарили: 0
Сообщений: 1
Дарья Сидорова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
6 сентября 2015 в 13:43
Ответ для Дарья Сидорова
Настюша Кирпичева
Профиль
Благодарили: 0
Сообщений: 1
Настюша Кирпичева
Профиль
Благодарили: 0
Сообщений: 1
1 3-
0
Спасибо
Ответить
2 сентября 2016 в 15:56
Ответ для Дарья Сидорова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
= ? · = ? = ===8
0
Спасибо
Ответить
22 апреля 2015 в 16:36
Амина Загребельная
Профиль
Благодарили: 0
Сообщений: 1
Амина Загребельная
Профиль
Благодарили: 0
Сообщений: 1
в морской воде содержится 5% соли, какую часть морской воды состовляет соль?
0
Спасибо
Ответить
14 апреля 2016 в 13:37
Ответ для Амина Загребельная
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В статье подробно описано, как это делается: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
А именно: «Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.»
5: 100=0,05=
0
Спасибо
Ответить
Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
– масса раствора = масса воды + масса соли;
– масса сплава равна сумме масс металлов, входящих в этот сплав;
– масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе – это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс – масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси – это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв – масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве – это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв – масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М – масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% – 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
В реальности, химики редко работают с чистыми веществами. В большинстве своем для работы, при проведении химических реакций, расчетов по ним используются различные растворы.
Раство́р — гомогенная (однородная) смесь, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия
Подробнее о процессе растворения мы поговорим в следующих статьях.
При решении расчетных задач нам нудно уметь находить количество чистого вещества, находящегося в растворе. Это необходимо затем, что, как правило, в химическое взаимодействие вступает вещество, а не дополнительные продукты, которое оно содержит: примеси, если это не чистое вещество, компоненты растворителя, или инертные для данного химического процесса компоненты смеси (если это смесь веществ).
Если мы работаем с 500 граммами раствора, в котором всего 10 грамм чистого вещества, то в расчеты мы берем 10 грамм, а не 500! – пример, почему необходимо уметь вычислять количественные характеристики чистого вещества.
Способы выражения концентрации растворов
Существуют различные способы выражения концентраций растворов. В задачах могут встретиться любые из них. Рассмотрим основные из них более подробно.
I. Массовая доля вещества
Массовая доля – отношение массы чистого вещества к массе всего раствора. Данная величина безразмерная (говорят доля от единицы, всегда меньше 1, или равна единице для чистого вещества), или выражается в %.
Очень часто можно встретить запись запись, например NaOH, 15% – это значит, что из всей массы раствора на долю гидроксида натрия (NaOH) приходится только 15 %.
Следует не забывать, что масса раствора = масса растворителя + масса чистого вещества.
Зная массовую долю вещества, нетрудно выразить формулу для расчета массы чистого вещества:
В некоторых задачах масса раствора может быть не дана в условии. В этом случае мы сами можем её задать. Как правило в таких случаях, мы задаём массу раствора как 100 г. Дальнейший расчет ведется уже исходя из заданной массы (если требуется перевести одну концентрацию в другую).
Приведем примеры задач:
Мы специально делаем подробное решение, чтобы отследить ход мыслей.
Решим аналогичную задачу:
Более часто встречаются задачи, в которых требуется приготовить раствор из другого раствора путем добавления чистого вещества (в этом случае концентрация увеличится), растворителя (концентрация уменьшится) или другого раствора (концентрация займёт промежуточное значение).
Рассчитайте массу соли, которую необходимо добавить к 150 г 10% -го раствора, чтобы концентрация полученного раствора стала 15%?
Данную задачу можно решать различными способами. В настоящий момент приведем только один (более длинный, но более понятный). Для решения таких задач другим способом мы подготовим видео.
Задачи, в которых добавляется растворитель – решаются проще.
Какое количество воды необходимо добавить к 200 г 15%-го раствора, чтобы его концентрация стала 10%?
Для решения задач, в которых смешиваются два раствора, имеющих различные концентрации, можно использовать следующий алгоритм:
1. Рассчитать количество чистого вещества в обоих растворах и сложить их.
2. Поделить полученное число на сумму масс растворов. Домножить на 100 %.
Решим для примера следующую задачу
Смешали 200 г 10%-го раствора серной кислоты и 100 г 20-% го. Какая массовая доля стала у получившегося раствора?
II. Молярная концентрация вещества
Молярная концентрация вещества – отношение количества вещества к объему раствора. Данная величина показывает нам, сколько (моль) вещества растворено в 1 литре раствора. Единица измерения – моль/л.
Обозначается молярная концентрация заглавной буквой C
В химической лаборатории очень часто для обозначения концентрации используется именно данная величина.
Очень часто, на химических склянках можно увидеть следующие обозначения:
Таким способом также обозначается молярная концентрация. Число перед буквой М обозначает концентрацию: 1 моль/л; 0,1 моль/л; 0,02 моль/л; 3 моль/л; 0,5 моль/л.
Можно также встретить в задачах такое обозначение, связанное с данной формой записи: молярный раствор (1 М) – раствор, концентрация которого составляет 1 моль/л. Децимолярный раствор (0,1 М) – 0,1 моль/л; сантимолярный раствор (0,01 М) – 0,01 моль/л.
Решим некоторые задачи, в которых используется молярная концентрация:
Для приготовления раствора сульфата натрия навеску, содержащую 14,2 г соли растворили в 500 мл воды и довели до метки.
Доведение до метки обозначает, что объем приготовленного раствора составляет (в данном случае) 500 мл.
Часто требуется рассчитать количество вещества:
Прежде чем проводить расчет по уравнению химических реакций, необходимо найти количество вещества.
III. Моляльная концентрация
Моляльная концентрация – отношение количества (моль) растворенного вещества к массе растворителя. Данная концентрация показывает нам, сколько моль вещества необходимо добавить к 1 кг растворителя (воды, например), чтобы получить нужную концентрации. Обозначается данная концентрация См, а измеряется в моль/кг(растворителя).
IV. Мольная доля
Мольная доля – отношение количества вещества к сумме количеств всех компонентов раствора. Данная физическая величина не имеет размерности.
Сумма всех мольных долей раствора равна “1”.
Данная физическая величина нашла широкое применение в химической химии для описания равновесных термодинамических процессов.
V. Титр
Титр – отношение массы вещества к единице объема (выраженного в миллилитрах). Титр показывает, сколько грамм вещества находится в каждом миллилитре раствора. обозначается как “Т” и измеряется в г/мл.
Титр – очень маленькая величина, так как в в 1 миллилитре раствора может находиться незначительное количество вещества.
Титр нашел широкое применение в аналитической химии.
В заключении
По данной теме существует огромное количество расчетных задач. Многие из них мы рассмотрим в следующих статьях. О пока…
Проверьте, как Вы усвоили материал.
Задание №1. Перейдите к гугл-форме и ответьте на вопросы (базовый уровень):
https://forms.gle/7u32uLfxRk1Yug7a8
Задание №2. Решите расчетные задачи: https://vk.com/page-205267346_56951920 (повышенный уровень)
Задание №3. Решите следующую задачу:
Какова молярная концентрация 12%-ного раствора серной кислоты (H2S04) с плотностью р = 1,08 г/см3. Рассчитайте титр данного вещества, моляльную концентрацию, мольную долю.
Отчет о решении задач пришли в беседу “Учебный класс”:
https://vk.me/join/DKsyQe2p0hJ2Wdoch1XOTwi_qZEJow1udOM=
Алгоритм нахождения массы растворенного вещества и массы воды, необходимые для приготовления раствора.
Задача.
Вычислить
массу соли и воды, необходимые для
приготовления 40 г раствора NаСl
с массовой долей 5%.
1.
Запишите условие задачи с помощью
общепринятых обозначений
Д
m р-ра
= 40г
ω = 5%
m (NаСl)
– ?
m (Н2О)
– ?
Решение:
1. Рассчитайте
массу растворенного вещества по формуле:
m в-ва=
ω ∙
m р-ра/100%
m
(NаСl)
= 5% · 40г/100% = 2г
2. Найдите массу
воды по разности между массой раствора
и массой растворенного вещества:
m р-ля
= m р-ра
– m в-ва
m
(Н2О)
= 40г – 2г = 38 г.
3.
Запишите
ответ.
Ответ: для
приготовления раствора необходимо
взять 2г соли и 38г воды.
Алгоритм нахождения массовой доли растворенного вещества при разбавлении (упаривании) раствора
Задача
К
15% раствору, масса которого 80г, добавили
30г воды. Какой стала массовая доля
растворённого вещества в полученном
растворе?
1. Запишите условие
задачи с помощью общепринятых обозначений.
Д
ω1
= 15%
mр-ра1=80г
m(Н2О)
= 30г
ω2-?
Решение:
1. В результате
разбавления (упаривания) раствора масса
раствора увеличилась (уменьшилась), а
вещества в нём осталось столько же.
Рассчитайте массу
растворённого вещества, преобразуя
формулу:
ω = m в-ва
/m р-ра
∙ 100%
m в-ва
= ω1·
mр-ра1
/100%
m
в-ва
= 15% · 80г = 12г
2. При разбавлении
раствора общая масса его увеличивается
(при упаривании – уменьшается).
Найдите массу
вновь полученного раствора:
m
р-ра2
= m
р-ра1 +
m(H2O)
m р-ра2
= 80г + 30г=110г
3. Рассчитайте
массовую долю растворённого вещества
в новом растворе:
ω2
= m в-ва /
m р-ра2
∙ 100%
ω2
= 12г/ 110г· 100% = 10,9%
4. Запишите ответ
Ответ:
массовая доля растворенного вещества
в растворе при разбавлении равна 10,9%
Алгоритм решения задач по «правилу креста»
Для получения
раствора с заданной массовой долей (%)
растворенного вещества путем смешивания
двух растворов с известной массовой
долей растворенного вещества пользуются
диагональной схемой (“правило креста”).
Сущность этого
метода состоит в том, что по диагонали
из большей величины массовой доли
растворенного вещества вычитают меньшую.
|
a с – в / с / в а – с |
где а – большая, |
Разности (с-в) и
(а-с) показывают, в каких соотношениях
нужно взять растворы а и в, чтобы получить
раствор с.
Если
для разбавления в качестве исходного
раствора используют чистый растворитель,
например, Н20,
то концентрация его принимается за 0 и
записывается с левой стороны диагональной
схемы.
Задача
Для
обработки рук хирурга, ран, послеоперационного
поля используется йодная настойка с
массовой долей 5%. В каком массовом
соотношении нужно смешать растворы с
массовыми долями йода 2,5% и 30%, чтобы
получить 330 г йодной настойки с массовой
долей йода 5%?
1. Запишите условие
задачи с помощью общепринятых обозначений.
Д
ω1
= 30%
ω2
= 2,5%
ω3
= 5%
m3
= 330г
m1
= ?
m2
= ?
Решение:
1. Составьте
“диагональную схему”. Для этого
запишите массовые доли исходных растворов
друг под другом, по левую сторону креста,
а в центре заданную массовую долю
раствора.
2,5
/
5
/
30
2.
Вычитают из бóльшей массовой доли
меньшую (30–5=25; 5–2,5=2,5) и находят результаты.
Записывают найденные
результаты с правой стороны диагональной
схемы: при возможности сокращают
полученные числа. В данном случае 25 в
десять раз больше, чем 2,5, то есть вместо
25 записывают 10, вместо 2,5 пишут 1.
30 2,5 (1)
/
5
/
2,5 25 (10)
Числа
(в данном случае 25 и 2,5 или 10 и 1)называют
массовыми числами. Массовые числа
показывают, в каком соотношении необходимо
взять исходные растворы, чтобы получить
раствор с массовой долей йода 5%.
3. Определите массу
30% и 2,5% раствора по формуле:
m
р-ра
= число частей · m3/
сумму массовых частей
m1(30%)
= 1· 330г /1+10 = 30г
m2(2,5%)
= 10 · 330г/ 1+10 = 300г
4. Запишите ответ.
Ответ:
для приготовления 330 г раствора с массовой
долей йода 5% необходимо смешать 300 г
раствора с массовой долей 2,5% и 30 г с
массовой долей 30%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #