Сила может подействовать только на материальное тело, которое обязательно имеет массу. Пользуясь вторым законом Ньютона, можно определить массу тела, на которое подействовала сила. В зависимости от природы силы для определения массы через силу могут понадобиться дополнительные величины.
Вам понадобится
- – акселерометр;
- – рулетка;
- – секундомер;
- – калькулятор.
Инструкция
Для расчета массы тела, на которое воздействует известная сила, воспользуйтесь соотношением, которое выводится из второго закона Ньютона. Для этого при помощи акселерометра измеряйте ускорение, которое получило тело в результате воздействия силы. Если этого прибора нет, измерьте скорость в начале и конце времени наблюдения за телом и поделите изменение скорости на время. Это и будет среднее ускорение тела за измеренный промежуток времени. Рассчитайте массу, поделив значение силы, действующей на тело F, на измеренное в м/с² ускорение a, m=F/a. Если значение силы взять в Ньютонах, то массу получите в килограммах.
Рассчитайте массу тела, на которое действует сила тяжести. Для этого подвесьте его на динамометр и по шкале определите силу, которая действует на тело. Это и будет сила тяжести. Для того чтобы определить массу тела, значение этой силы Fт поделите на ускорение свободного падения g≈9,81 м/с², m=F/g. Для удобства в расчетах можно брать значение g≈10 м/с² в том случае, если не требуется высокая точность определения значения массы в килограммах.
Когда тело движется по круговой траектории с постоянной скоростью, на него тоже действует сила. Если известна ее величина, найдите массу тела, движущегося по круговой траектории. Для этого измерьте или рассчитайте скорость движения тела. Измерение производите спидометром, если это возможно. Чтобы рассчитать скорость, померьте радиус траектории тела рулеткой или линейкой R и время полного оборота Т при помощи секундомера, это называется период вращения. Скорость будет равна произведению радиуса на число 6,28, поделенному на период. Найдите массу, умножив силу F на радиус траектории движения тела и поделив результат на квадрат его скорости m=F•R/v². Для получения результата в килограммах, скорость измеряйте в метрах в секунду, радиус – в метрах, а силу – в Ньютонах.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В статье обсуждаются несколько подходов и несколько примеров того, как рассчитать массу по силе и расстоянию.
Сэр Исаак Ньютон сформулировал многочисленные законы и теории которые дают нам различные подходы к вычислению массы тела с расстояния, пройденного под действием силы. Плюс кинематические уравнения движения и формула работы-энергии Помогите нам определить массу по силе и расстоянию.
Рассчитайте массу, используя закон всемирного тяготения Ньютона
Мы можем вычислить массу, используя закон всемирного тяготения Ньютона, следующим образом:
к вычислить массу через силу и расстояния, мы можем использовать законы тяготения Ньютона, которые гласят: «сила гравитации, действующая между двумя телами, прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между центрами масс».
Гравитация универсальна. Это означает, что все объекты во Вселенной притягиваются друг к другу гравитацией, и Закон всемирного тяготения Ньютона объясняет эту универсальность гравитации. По закону всемирного тяготения
Fg ∝м1m2/r2
Где, Fg = сила тяжести между двумя объектами
m1 масса объекта 1
m2 масса объекта 2
r – расстояние, разделяющее центры обоих объектов ..
(Кредит: Shutterstock)
Поскольку сила тяжести прямо пропорциональна массам обоих объектов, более крупные объекты будут притягивать друг друга с более значительной силой тяжести.
Переписывая формулу в терминах константы пропорциональности,
Fg=G*(м1m2/r2)………………(1)
Где, G есть универсальная гравитационная постоянная с постоянным значением 6.67 x 10-11 Nm2/ кг2.
В уравнении (1), как и постоянное значение G, у нас также есть постоянное значение массы объекта 2, которое является массой земли; как и в большинстве случаев, мы вычисляем силу тяжести любого объекта относительно земли. Следовательно, постоянное значение массы Земли равно m2 есть, 5.98 x 1024 кг.
Из уравнения (1),
Если мы определим расстояние d и силу тяжести на объекте Fg, мы можем вычислить его массу m1 используя закон всемирного тяготения Ньютона.
Сила тяжести между землей и мальчиком составляет 680 Н, когда он стоит на расстоянии 6.38 х 10.6м от центра Земли. Определите массу мальчика, стоящего на земле.
Данный:
Fg = 680 Н
г = 6.38 х 106 m
m2= 5.98 x 1024 kg
G = 6.67 х 10-11 Nm2/ кг2
Найти: m1 =?
Формула:
Fg=G*(м1m2/r2)
Решения:
Масса мальчика, стоящего на земле, рассчитывается по формуле закона всемирного тяготения:
Fg=G*(м1m2/r2)
Переставляем по м1,
m1=(43.384*108)/(39.904*1013)
m1 = 108.67 кг
Масса стоящего на земле мальчика 108.67 кг.
Расчет массы с использованием второго кинематического уравнения движения
Мы можем вычислить массу, используя второй закон движения Ньютона:
Чтобы вычислить массу объекта, мы можем использовать популярную формулу второго закона движения Ньютона, которая показывает связь между ускорением, силой и массой. Затем мы можем реализовать это во втором кинематическом уравнении движения, которое касается расстояния.
Второй закон движения объясняет, что объект ускоряется (а) с трудом, когда сила (F) применяется к объекту, имеющему массу m.
а=Ф/м………………… (2)
(Кредит: Shutterstock)
Второе кинематическое уравнение движения о расстоянии d есть;
d=ut+(1/2)в2…………………. (3)
Подставляя уравнение (3) в уравнение выше, получаем
d=ut+(Ft2/ 2м)
If мы определяем расстояние (d), пройденное объектом за время (t), когда на него действует сила (F), мы можем вычислить его массу, используя второе кинематическое уравнение движения.
Чистая сила 10 Н действует на объект, который преодолевает расстояние 40 м с начальной скоростью 1 м / с за 5 с. Рассчитайте массу объекта.
Данный:
F = 10 Н
d = 40 м
u = 1 м / с
t = 5 с
Найти: м =?
Формула:
d=ut+(1/2)в2
Решения:
Массу объекта можно рассчитать, используя второе кинематическое уравнение движения.
d=ut+(1/2)в2
Согласно второму закону Ньютона, a=F/m
Подставляя значение ‘a’ в уравнение кинематики, получаем
d=ut+(Ft2/ 2м)
Подставляя все значения,
Масса объекта 3.57 кг.
Расчет массы с использованием третьего кинематического уравнения движения
Мы можем рассчитать массу, используя третье кинематическое уравнение движения.
Чтобы вычислить массу объекта, мы можем реализовать формулу второго закона движения Ньютона в третьем кинематическом уравнении движения, которое касается скорости.
Третье кинематическое уравнение движения о скорости v есть,
v2=u2+2реклама………………….(4)
Реализуем второй закон движения Ньютона (2) в третье кинематическое уравнение движения (4),
v2=u2+(2fd/м)………….(5)
Предположим, мы определяем расстояние (d), которое проходит объект, когда его скорость v изменяется от начальной скорости u из-за силы F. В этом случае мы можем вычислить его массу, используя третье кинематическое уравнение движения.
Объект движется по прямой траектории в 5 м от исходного положения со скоростью 5 м / с, когда сила 50 Н приложена к тому же объекту в состоянии покоя. Рассчитайте массу объекта.
Данный:
d = 5м
v = 5 м / с
u = 0, поскольку объект изначально находится в состоянии покоя.
F = 50 Н
Найти: м =?
Формула:
v2=u2+2объявление
Решения:
Массу объекта можно рассчитать по третьему кинематическому уравнению движения,
v2=u2+2объявление
Подставляя значение ‘a’ в уравнение кинематики, получаем
v2=u2+(2fd/м)
Подставляя все значения,
Масса объекта 20 кг.
Рассчитайте массу с помощью формулы работы-энергии
Мы можем вычислить массу, используя следующую формулу работы-энергии:
Чтобы вычислить массу объекта, мы можем использовать формулу работы-энергии, которая показывает, что работа, выполняемая над объектом, равна его преобразованию кинетической энергии, когда он перемещается на определенное расстояние из-за приложенной силы.
(Кредит: Shutterstock)
Выполненная работа рассчитывается как побочный продукт приложенной силы и пройденного расстояния.
W = Fd ……………………. (6)
Проделанная работа – это преобразование кинетической энергии объекта. Следовательно, проделанная работа равна кинетической энергии,
W = KE
Вт=(1/2)мв2…………………. (7)
Подставляя значение W (6),
Fd==(1/2)мв2 …………… .. (8)
Если мы определим расстояние (d), которое проходит объект со скоростью v, когда к нему применяется сила (F), мы можем вычислить его массу, используя формулу работы-энергии.
Примечание: здесь мы считаем, что сила трения незначительна.
Коробка скользит примерно на 10 м по горизонтальной поверхности со скоростью 20 м / с, когда мы прикладываем силу толчка 50 Н. Рассчитайте массу ящика.
Данный:
d = 10 м
v = 20 м / с
F = 50 Н
Найти: m =?
Формула:
Вт=(1/2)мв2
Решения:
Массу ящика можно рассчитать по формуле работы-энергии:
Вт=(1/2)мв2
Подставляя стоимость проделанной работы W,
Fд=(1/2)мв2
Преобразуя уравнение для ‘m’,
m=2Fd/v2
Подставляя все значения,
Масса ящика 2.5 кг.
Легче всего решать задачу, если все приложенные к телу силы параллельны – тогда можно получить ответ, используя лишь правило моментов. Если же силы непараллельные, то иногда для получения ответа требуется дополнительно применять второй закон Ньютона.
Параллельные силы
Алгоритм решения задач на правило моментов (параллельные силы)
- Выполнить чертеж. Указать на нем все силы с точкой их приложения и направлением действия. В этом вам поможет таблица.
| Сила | Точка приложения | Направление |
| Сила тяжести, действующая на груз | Центр груза | Вертикально вниз |
| Сила тяжести, действующая на однородный стержень | Центр тяжести | Вертикально вниз |
| Сила тяжести, действующая на неоднородный стержень | Центр масс, положение которого указывают в условии задачи | Вертикально вниз |
| Вес | Точка опоры или подвеса | Вес тела направлен противоположно вектору силы нормальной реакции опоры или вектору силы натяжения подвеса |
| Сила реакции опоры | Точка соприкосновения стержня и опоры | Перпендикулярно вверх |
| Сила натяжения нити | Точка соединения с подвесом | Вдоль оси подвеса |
- Выбрать положение оси вращения. Обычно ось выбирают в месте, где находится неизвестная сила или сила, искать которую не нужно.
- Указать значение плеч. Если в задаче нужно указать некоторое расстояние (к примеру, от центра стержня или от места приложения некоторой силы), то это расстояние следует обозначать за x. Размер плеч сил нужно определять с учетом размеров стержня и расстояния x.
- Записать правило моментов и решить задачу.
Типовы задачи на правило моментов при параллельных силах
| Прямая неоднородная балка длиной l и массой m подвешена за концы на вертикально натянутых тросах. Балка занимает горизонтальное положение. Найдите силу натяжения первого троса T2, если центр тяжести балки находится на расстоянии a от левого конца балки. |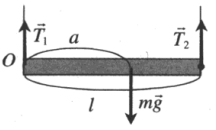 
Для решения задачи в качестве положения оси вращения удобно выбрать точку приложения силы натяжения первого троса (потому что ее искать не нужно). Тогда плечом силы тяжести будет расстояние a, а плечом силы натяжения второго троса — l. Поэтому правило моментов можно записать так: T2l = mga T2 = mga/l |
| Рельс длиной l и массой m поднимают равномерно в горизонтальном положении на двух вертикальных тросах, первый из которых укреплен на конце рельса, а второй — на расстоянии x от другого конца. Определите натяжение второго троса. |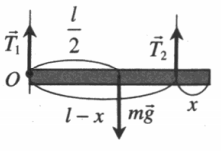 
В этой задаче положение оси вращения также удобно выбрать в точке О, соответствующей точке приложения силы натяжения нити первого троса (так как ее искать не нужно). Тогда плечом силы натяжения второго троса будет служить разность длины рельса и расстояния x, а плечом силы тяжести — половина длины рельса. Поэтому правило моментов примет вид: mgl/2 = T2(l – x) T2 = mgl2(l−x) |
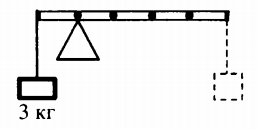
Пример №1. К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рисунок). Стержень расположили на опоре, отстоящей от груза на 0,2 длины. Груз какой массы надо подвесить к правому концу, чтобы стержень находился в равновесии?
Условие равновесие будет выполняться, если произведение силы тяжести первого груза на ее плечо будет равно произведению силы тяжести второго груза на ее плечо:
Fтяж1d1 = Fтяж2d2
Согласно рисунку, второй груз будет подвешен на расстоянии 0,8 от опоры. Следовательно:
Fтяж2=Fтяж2d1d2=m1gd1d2
m2g=m1gd1d2
m2=m1d1d2=3·0,20,8=0,75 (кг)
Непараллельные силы
Алгоритм решения задач на правило моментов (непараллельные силы)
- Выполнить чертеж и указать все силы. Правильно определить точку приложения и направление сил поможет таблица:
| Сила | Точка приложения | Направление |
| Сила реакции опоры | Точка соприкосновения с опорой | Перпендикулярно плоскости опоры |
| Сила трения покоя | Точка соприкосновения с опорой | В сторону возможного движения |
| Сила тяжести | Центр масс (у однородных тел центр масс совпадает с центром тела) | Вертикально вниз |
| Архимедова сила | Центр масс погруженной части тела | Вертикально вверх |
- Определить плечи сил как кратчайшее расстояние между осью вращения и направлением действия силы.
- Записать правило моментов и решить задачу.
Внимание! Иногда для решения задачи может потребоваться использование второго закона Ньютона в проекциях на оси Ox и Oy.
Типовы задачи на правило моментов при непараллельных силах
| Рабочий удерживает за один конец доску массой m так, что она образует угол α с горизонтом, опираясь о землю другим концом. С какой силой рабочий удерживает доску, если эта сила перпендикулярна доске? |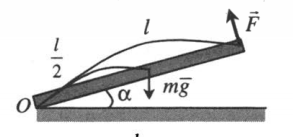 
За точку равновесия примем точку касания доски с землей. Плечо силы тяжести будет равно нижнему катету треугольника, образованного при опускании перпендикуляра к земле из точки приложения этой силы: d1 = l cosα/2 Плечо силы, с которой рабочий поднимает доску, равно длине доски: d2 = l Отсюда: mglcosα2=Fl F=2lmglcosα=2mgcosα |
| В гладкий высокий цилиндрический стакан с внутренним радиусом R помещают карандаш длиной l и массой m. С какой силой действует на стакан верхний конец карандаша? |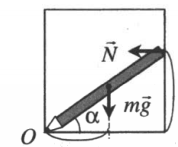 
За точку равновесия примем нижнюю точку карандаша. Сила давления верхнего конца карандаша на стакан по модулю будет равна силе нормальной реакции опоры в этой точке. Поэтому плечо ее силы будет равно произведению длины карандаша на синус угла между ним и дном стакана: d1 = l sinα Минимальным расстоянием между линией действия силы тяжести и точкой равновесия будет половина произведения длины карандаша на косинус угла между ним и дном стакана: d2 = l сosα/2 Отсюда: Nl sinα = mgl сosα/2 N=mglcosα2lsinα Плечо силы тяжести также равно радиусу стакана, а плечо силы реакции опоры можно найти из теоремы Пифагора. Отсюда: N=mgR√l2−4R2 |
| Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу надо приложить, чтобы оно могло подняться на ступеньку? Сила трения равна нулю. |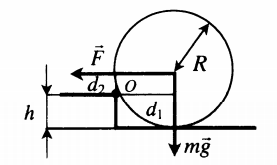 
За точку равновесия примем точку касания колеса со ступенькой. Плечо силы тяжести является катетом треугольника, образованного с радиусом колеса и плечом прикладываемой силы. Плечо этой силы равно разности радиуса и высоты ступеньки. d1=√R2−d22 d2 = R – h Отсюда: mg√R2−d22=F(R−h) F=mg√R2−d22R−h=mg√h(2R−h)R−h |
| Лестница массой m приставлена к гладкой вертикальной стене пол углом α. Найдите силу давления лестницы на стену. Центр тяжести лестницы находится в ее середине. |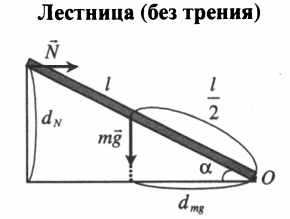 
Плечо силы тяжести равно половине произведения длины лестницы на косинус угла α. Плечо силы реакции опоры равно произведению этой длины на синус α. Поэтому правило моментов записывается так: Nlsinα=mglcosα2 Отсюда: N=mglcosα2lsinα=mg2tanα |
| Лестница длиной l приставлена к идеально гладкой стене под углом α к горизонту. Коэффициент трения между лестницей и полом μ. На какое расстояние x вдоль лестницы может поднять человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь. |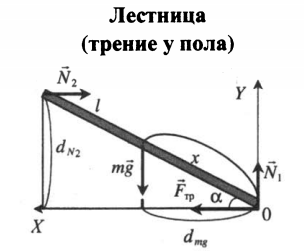 
Правило моментов: mgxcosα=N2lsinα Второй закон Ньютона в проекциях на оси Ox и Oy соответственно: Fтр – N2 = 0 N1 – mg = 0 Сила трения: Fтр = μmg = N2 Следовательно: mgxcosα=μmglsinα x=μmglsinαmgxcosα=μltanα |
| Однородная лестница приставлена к стене. При каком наименьшем угле α между лестницей и горизонтальным полом лестница сохранит равновесие, если коэффициент трения между лестницей и полом μ1, а между лестницей и стеной — μ2? |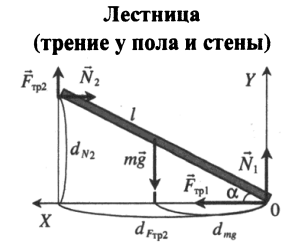 
Правило моментов: mgl2cosα=Fтр2lcosα+N2lsinα Второй закон Ньютона в проекциях на ось Ox: Fтр1 – N2 = 0 μ1N1 – N2 = 0 На ось Oy: Fтр2 + N1 – mg = 0 μ2N2 +N2μ1 = mg N2(μ2+1μ1)=mg N2=mgμ2+1μ1=mgμ1μ1μ2+1 Fтр2=mg−N1=mg−N2μ1=mg−mgμ1μ2+1=mg(1−1μ1μ2+1) mgl2cosα=mg(1−1μ1μ2+1)lcosα+mgμ1μ1μ2+1lcosα Преобразуем выражение и получим: tanα=1−μ1μ21μ1 |
| Какую минимальную горизонтальную силу нужно приложить к верхнему ребру куба массой m, находящегося на горизонтальной плоскости, чтобы перекинуть его через нижнее ребро? |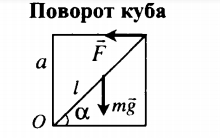 
Правило моментов примет вид: mgl2cosα=Flsinα У куба угол α равен 45 градусам, а синус и косинус этого угла равны. Длины диагонали взаимоуничтожаются. Остается: F=mg2 |
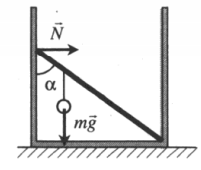
Пример №2. Невесомый стержень длиной 1 м, находящийся в ящике с гладким дном и стенками, составляет угол α = 45о с вертикалью (см. рисунок). К стержню на расстоянии 25 см от его левого конца подвешен на нити шар массой 2 кг. Каков модуль силы N, действующий на стержень со стороны левой стенки ящика?
25 см = 0,25 м
Пусть точкой равновесия будет точка касания нижнего конца стержня с дном ящика. Тогда плечом силы тяжести будет:
d1 = (l – 0,25)sinα
Плечом силы реакции опоры будет:
d2 = l cosα
Запишем правило моментов:
mg(l−0,25)sinα=Nlcosα
Отсюда:
N=mg(l−0,25)sinαlcosα
Так как косинус и синус угла 45о равны, получим:
N=mg(l−0,25)l=2·10(1−0,25)1=15 (Н)
Задание EF17982
Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
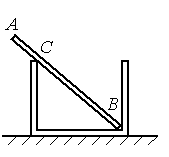
Ответ:
а) 0,3 Н
б) 0,25 Н
в) 0,6 Н
г) 0,13 Н
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
- Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса стержня: m = 100 г.
- Модуль силы, с которой стержень давит на стенку сосуда в точке С: FC = 0,5 Н.
- Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: FBy = 0,6 Н.
Переведем единицы измерения в СИ:
100 г = 0,1 кг
Выполним чертеж:
Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:
- сила тяжести (mg);
- сила реакции опоры в точке С (FC);
- сила реакции опоры в точке В (FВ).
Поэтому:
m→g+→FC+→FB=0
Запишем проекции на оси Ox и Oy соответственно:
FCx=FBx
FCy+FBy=mg
Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:
FCx=√F2C−F2Cy
Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:
FCy=mg−FBy
Отсюда:
FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2
Подставим известные данные и вычислим:
FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18697
Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?
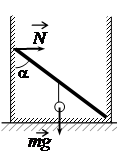
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Угол между стержнем и стенкой ящика: α = 45o.
• Масса шарика: m = 1 кг.
Чтобы записать правило моментов, нужно определить плечи силы тяжести и силы упругости. В качестве точки равновесия выберем точку опоры нижнего конца стержня. Тогда плечо силы тяжести будет равно произведению половины длины стержня на косинус угла между дном ящика и стержнем. Он тоже будет равен 45 градусам, так как он равен разности 180 градусов и угла α = 45o. Отсюда:
dmg=l2cosα
Плечо силы упругости будет равно расстоянию от дна ящика до верхней точки стержня. Оно определяется как произведение длины стержня на синус угла α:
dN=lsinα
Запишем правило моментов:
mgl2cosα=Nlsinα
Отсюда:
N=mgl2lsinαcosα
Длина стержня в числителе и знаменателе сократится, косинус и синус угла тоже, так как при 45 градусах они одинаковые. Следовательно:
N=mg2=1·102=5 (Н)
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.9k
F = m * a — Сила равна произведению массы на ускорение. Масса — скалярная физическая величина, измеряющая количество вещества в теле, мера инерции тела по отношению к действующей на него силе. m = F / a — Масса равна отношению силы к ускорения.
Как вычислить массу в физике?
Масса тела выражается через плотность и объем следующей формулой: Масса тела — есть произведение плотности вещества из которого состоит тело на его объем.
Как найти массу через силу?
Для вычисления веса используйте формулу Р = mg.
Так как вес является силой, X Источник информации эту формулу можно записать и как F = mg. P или F — соответственно, вес или сила (измеряется в ньютонах, Н). m — масса тела (измеряется в килограммах, кг).
Как найти массу с помощью скорости?
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом: m = 2 ⋅ E кин v 2 и v = 2 ⋅ E кин m . С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.
Как найти массу и силу тяжести?
Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения. Для тела массой m=400 г =0.4 кг сила тяжести составит Fт=0.4*10=4 Н.
Чему равна масса в физике?
Масса тела равна его плотности умноженной на объём. – его объём. Единица измерения массы – килограмм (кг). Плотность вещества определяется свойствами молекул, из которых оно состоит и их взаимным расположением (молекулярной структурой вещества).
Как найти массу?
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Как найти массу тела по его весу?
Для расчета индекса массы тела требуется вес в килограммах, поделить на рост в метрах, взятый в квадрат, т. е. ИМТ = вес (кг)/рост (м)2.
Как по плотности и объему найти массу тела?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Как найти массу тела имея силу и ускорение?
m = F / a — Масса равна отношению силы к ускорения.
Как найти массу тела в физике формула?
Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.
Как можно найти массу вещества?
И наоборот, массу вещества определяют как произведение молярной массы на количество вещества: m = n . M. Так, масса 0,1 моля Na составляет 0,1 моль×23 г/моль = 2,3 Молярная масса численно всегда совпадает с молекулярной массой (или атомной массой — если вещество состоит не из молекул, а из атомов).
Как вычислить силу тяжести своего тела?
Силу, с которой Земля притягивает тела, можно рассчитать по формуле F = m ⋅ g , где m — масса тела, а g — ускорение свободного падения.
Масса – стержень
Cтраница 2
Массой стержня и нити, а также трением между поверхностями стержня и шаров пренебречь.
[16]
Массой стержня 0В, шарннрно закрепленного в точке О, пренебречь. В положении равновесия стержень горизонтален.
[17]
Массой стержня 0В, шарнирно закрепленного в точке О, пре – – небречь. В положении равновесия стержень горизонтален.
[18]
Если масса стержня мала по сравнению с массой ударяющего груза Р, то величина Т мала по сравнению с Г и ее можно не учитывать.
[19]
Если масса стержня мала по сравнению с массами тх и щ, то ею можно пренебречь.
[21]
Если масса стержня мала по сравнению с массами / HJ и т %, то ею можно пренебречь.
[23]
Центр масс стержня займет низшее положение, когда стержень встанет вертикально.
[24]
Центр масс стержня лежит на его оси, так как это ось его симметрии.
[25]
Обозначая массу стержня через М, вычислим все входящие в это уравнение величины.
[26]
Определить массу стержня длины / 10 м, если линейная плотность стержня меняется по закону б 6 – [ – 0 3.x: кг 1м, где х – расстояние от одного из концов стержня.
[27]
Определить массу стержня длины / 10 м, если линейная плотность стержня меняется по закону 6 6 – – 0Злг KSJM, где х – расстояние от одного из концов стержня.
[28]
Определить массу стержня длины / 10 м, если линейная плотность стержня меняется по закону 6 6 0 3л: кг / м, где х – расстояние от одного из концов стержня.
[29]
Определить массу стержня длины / 10 м, если линейная плотность стержня меняется по закону 6 6 0 3х кг / м, где х – расстояние от одного из концов стержня.
[30]
Страницы:
1
2
3
4
