Как найти массу тела через импульс

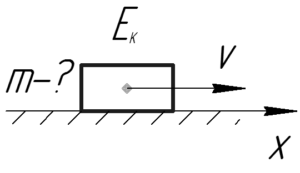
Условие задачи:

Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс 8 кг·м/с.

Задача №2.7.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(E_к=16) Дж, (p=8) кг·м/с, (m-?)

Решение задачи:

Кинетическую энергию тела, движущегося поступательно, определяют по формуле:

[{E_к} = frac{{m{upsilon ^2}}}{2}]

Домножим и числитель, и знаменатель дроби в правой части на массу (m), тогда:

[{E_к} = frac{{{m^2}{upsilon ^2}}}{{2m}}]

Известно, что произведение массы тела (m) на скорость (upsilon) есть такая физическая величина, называемая импульсом (p). Поэтому:

[{E_к} = frac{{{p^2}}}{{2m}}]

В итоге массу тела найдем из следующей формулы:

[m = frac{{{p^2}}}{{2{E_к}}}]

Считаем ответ:

[m = frac{{{8^2}}}{{2 cdot 16}} = 2;кг]

Ответ: 2 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.15 Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести
2.7.18 Автомобиль массой 1,5 т едет со стоянки с постоянным ускорением 2 м/с2. Коэффициент

Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.

В результате чего были выведена новая формула второго закона ньютона а = F /m, 

Что такое второй закон Ньютона, масса и вес тела

Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.

Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

Ускорение от величины силы

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at₂) : 2 определим ускорение a.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку

a₁ : a₂ = F₁ : F₂

ИЛИ

а ~ F.

Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.

Зависимость ускорения от массы

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).

Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть

(a₁/a₂) = (m₂/m₁), или а ~ (1/m)

Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).

Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):

а = F /m

где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.

Результирующая сила F равна векторной сумме всех сил, приложенных к телу;

F = mа.

Следовательно, сила равна произведению массы на ускорение.

Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение

а = (υ₂ — υ₁) / (t₂ — t₁)

подставим это выражение в уравнение второго закона Ньютона. Получим

F = ma = (mυ₂ — mυ₁) / (t₂ — t₁) = (∆(mυ))/∆t

Что такое импульс

Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).

Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)

F = (∆(mυ))/∆t

Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.

Из второго закона Ньютона вытекает следующее определение массы. Из равенства 

a₁/a₂= m₂/m₁ 

видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.

Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.

Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

где m — масса тела, движущегося со скоростью υ; m₀ — масса этого же тела, находящегося в покое; с = 3 • 10⁸м/с скорость света в вакууме.

Проанализируем данное уравнение:

1. Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m₀, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
2. Если υ ≈ с, то υ₂/с₂ ≈ 1, тогда т = m₀/0— отсюда вытекает, что m → ∞.

По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.

Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.

Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.

Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.

Масса тела с ростом скорости

Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.

Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.

Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже). 

Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ₀ = 0) называется свободным падением. 

Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.

Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.

Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с²), то применяя второй закон динамики, получим

P = mg.

Выразим с помощью этой формулы веса двух различных тел. Тогда:

P₁ = m₁g и Р₂ = m₂g. Разделив почленно эти два равенства, будем иметь

P₁/P₂ = m₁/m₂

Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

Задачи на второй закон ньютона

1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с².

Дано:
m = 1000 кг
a = 1 м/с²

Найти: F — ?

Решение:

Запишем второй закон Ньютона :

F = mа.

F = 1000 кг • 1 м/с² = 1000 Н

Ответ: 1000 Н.

2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.

Дано:

m = 0,2 кг,

F = 70Н

Найти:

a — ?

Решение:

Запишем второй закон Ньютона :

F = mа.

Следовательно а = F / m.

а = 70Н : 0,2 кг = 350 м/с.

Ответ: а = 350 м/с.

---

Статья на тему Второй закон Ньютона

Эйнштейн показал,
что масса тела зависит от его скорости:

где
m₀ –
масса тела в той системе отсчета, где
тело покоится (масса покоя); m – масса
тела в той системе, относительно которой
тело движется (релятивистская масса);

– скорость тела относительно системы
отсчета, в которой определяется масса
m.

Релятивистский
импульс

где m – релятивистская масса.

Закон взаимосвязи
массы и энергии:

,

где
m – релятивистская масса; Е – полная
энергия материального объекта.

Кинетическая
энергия объекта

,

где
–
полная энергия;–
энергия покоя.

Из
закона взаимосвязи массы и энергии
следует, что всякое изменение массы
тела на m
сопровождается изменением его энергии
на E:

E=mc².

Примеры решения задач

Задача
1 Уравнение
движения точки по прямой имеет вид: x =
A+Bt+Ct³,
где А = 4 м, В = 2 м/c, С = 0,2 м/с³.
Найти: 1) положение точки в моменты
времени t = 2 c и t = 5 с; 2) среднюю скорость
за время, протекшее между этими моментами;
3) мгновенные скорости в указан­ные
моменты времени; 4) среднее ускорение
за указанный промежуток вре­мени; 5)
мгно­венные ускорения в указанные
моменты времени.

Дано:

x = A + Bt + Ct3 A = 4 м B = 2 м/c C = 0,2 м/c3 t1 = 2 c; t2 = 5 c	Решение 1. Чтобы найти координаты точки, надо в уравнение дви­же­­­ния подставить значения t1 и t2: x1 = (4+22+0,223) м = 9,6 м, x2 = (4+25+0,253) м = 39 м.
x1, x2, <>- ? 1, 2 – ? <a>, a1, a2 – ?	2. Средняя скорость,

м/с = 9,8 м/с.

3.
Мгновенные скорости найдем,
продифференцировав по времени уравнение
движения:

₁
= (2+30,22²)
м/с = 4,4 м/c;

₂
= (2+30,25²)
м/с = 17 м/с.

4.
Среднее ускорение
,

м/c²
= 4,2 м/с².

5.
Мгновенное ускорение получим, если
продифференцируем по времени выражение
для скорости: a = 23Ct
= 6Ct.

a₁
= 60,22
м/c² =
2,4 м/с²;

a₂
= 60,25
м/с² =
6 м/с².

Ответ:
x₁ =
9,6 м; x₂ =
39 м; 
= 9,8 м/с; ₁
= 4,4 м/c; ₂
= 17 м/с; а
= 4,2 м/с²;
a₁ =
2,4 м/с²;
a₂ =
6 м/с².

Задача
2 Маховик
вращается равноускоренно. Найти угол
,
ко­то­рый составляет вектор полного
ускорения
любой
точки маховика с радиусом в тот момент,
когда маховик совершит первые N=2 оборота.

Дано:

0 = 0 N = 2  = const	Решение Разложив вектор точки М на тангенци­аль­ноеи нормальноеуско­ре­ния, видим, что иско­мый угол определяется соотно­шением tg=a/an.
 – ?

Поскольку
в условии дано лишь число оборотов,
перейдем к угловым величинам. Применив
формулы: a_
= R,
a_n =
²R,
где R – радиус маховика, получим

tg
=

так
как маховик вращается равноускоренно,
найдем связь между величинами 
и ;

Поскольку
₀
= 0; 
= 2N,
то ²
= 22N
= 4N.

Подставим
это значение в формулу, получим:

 2,3.

Ответ:


2,3.

Задача
3 Две гири
с массами m₁
= 2 кг и m₂
= 1 кг
соединены нитью, пе­ре­ки­ну­той
через невесомый блок. Найти ускорение
a, с которым движутся гири, и силу натяжения
нити
. Трением в блоке пренебречь.

Дано:

m1 = 2 кг m2 = 1 кг	Решение Воспользуемся для решения задачи основным законом динамики где – равнодействующая всех сил, действующих на тело.
a, FН – ?

На тело 1 и тело 2 действуют только две
силы – сила тяжести и сила

натяжения
нити. Для первого тела имеем

(1)

для второго тела

.
(2)

Так
как сила трения в блоке отсутствует,

.

Ускорения
тел а₁
и а₂
направлены в противоположные стороны
и равны по модулю:

.

Получаем
из выражений (1) и (2) систему уравнений

Выберем
ось Х, как показано на рисунке и запишем
полученную систему уравнений

в
проекции на ось Х

Решая
эту систему относительно а и F_Н,
получаем:

=
3,3 м/с²;

=
13 Н.

Ответ:
a
= 3,3 м/c²
; F_H
= 13 Н.

Задача
4 К ободу
однородного диска радиусом R=0,2 м
прило­жена каса­тель­ная сила
F=98,1 Н. При вращении на диск
действует момент сил трения

М_ТР=4,9
Нм.
Найти массу m диска, если известно, что
диск вращается с угловым ускорением
=100
рад/с².

Дано:

R = 0,2 м F = 98,1 Н MТР = 4,9 Нм  = 100 рад / c2	Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости: , где  момент сил, приложенных к телу,
m – ?

относительно
выбранной оси ( M_F
– момент
силы F, M_тр
– момент сил трения);

момент
инерции диска.

Учитывая,
что M_F=FR,
получаем
.

Отсюда
;
m = 7,4 кг.

Ответ:
m
= 7,4 кг.

Задача 5

Вагон массой 20 т,
движущийся равнозамедленно, под действием
силы трения в 6 кН через некоторое время
останавливается. Начальная скорость
вагона равна 54 км/ч. Найти работу сил
трения и расстояние, которое вагон
пройдет до остановки.

Дано:

m = 20  10 3 кг Fтр = 6  10 3 Н  = 15 м/c	Решение По закону сохранения механической энергии изменение полной механической энергии определяется работой неконсервативных сил, то есть .
AТР – ? r – ?	Так как механическая энергия вагона равна его кинети­ческой энергии, в качестве неконсервативной силы выступает сила

трения.
Так как в конце пути скорость вагона
равна нулю, то

.

Итак:
=-2250
кДж.

По
определению, для работы, совершаемой
постоянной силой трения:

м.

Ответ:
r
= 375 м.

Задача
6 После
упругого удара нейтрона о ядро атома
углерода он движется в направлении,
перпендикулярном начальному. Считая,
что масса М ядра углерода в n=12 раз больше
массы m нейтрона, определить, во сколько
раз уменьшается энергия нейтрона в
результате удара.

Дано:

	Решение Ведем обозначения: 1 – скорость нейтрона до удара, 1 – после удара; 2 – скорость ядра углерода после удара (до удара она равна нулю).
 – ?

По
законам сохранения импульса и энергии
соответственно имеем:

По
условию задачи требуется найти отношение

Из
треугольника импульсов (смотри рисунок)

имеем:
(m₁)²+(m₁)²=(M₂)².

С
учетом записанных выражений, а также
соотношения n=M/m получим

₁²-₁²=n₂²;

₁²+₁²=n²₂².

Разделив
почленно последние равенства, получаем

.

Отсюда

=1,18.

Ответ:

= 1,18.

Задача
7 Круглая
платформа радиусом R=1,0 м, момент инерции
которой J=130
кгм²,
вращается по инерции вокруг вертикальной
оси, делая n₁=1,0
об/с. На краю платформы стоит человек,
масса которого m=70 кг. Сколько оборотов
в секунду n₂
будет совершать платформа, если человек
перейдет в её центр? Момент инерции
человека рассчитывать как для материальной
точки.

Дано:

R= 1м J = 130 кг  м2 n1 = 1c-1 m = 70 кг	Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме:
n2 – ?

L₁
= L₂
,
(1)

где
L₁

импульс системы «платформа + человек
на краю платформы»,
L₂

импульс системы
«платформа + человек в центре платформы».

L₁
=
J₁₁
=
(J+mR²)2n₁,
(2)

L₂
=
J₂₂
=
J2n₂,
(3)

где
mR²

момент инерции человека, J₁
= J+mR²

момент инерции системы «платформа +
человек на краю платформы», J₂

момент инерции системы «платформа +
человек в центре платформы», ₁
и ₂

соответствующие угловые скорости
системы. Решая систему уравнений (1) 
(3), получаем

n₂
= n₁(J+mR²)/J
= 1,5 об/с.

Ответ:
n₂
= 1,5 с^-1.

Задача 8

Определить
кинетическую энергию (в электронвольтах)
и релятивистский импульс электрона,
движущегося со скоростью 
= 0,9 c (с = 310⁸
м/с 
скорость света в вакууме).

Дано:

 = 0,9 c	Решение Так как скорость частицы сопоставима по значению со скоростью света в вакууме, то частицу нельзя считать классической. Для нахождения кинетической энергии воспользуемся формулой:
ЕК, р – ?

,

где

масса покоя электрона.

Получаем

Так
как
,то

Можно
было найти значение кинетической энергии
сразу в электрон вольтах, учитывая, что
энергия покоя электрона

Релятивистский
импульс находим по формуле

,

.

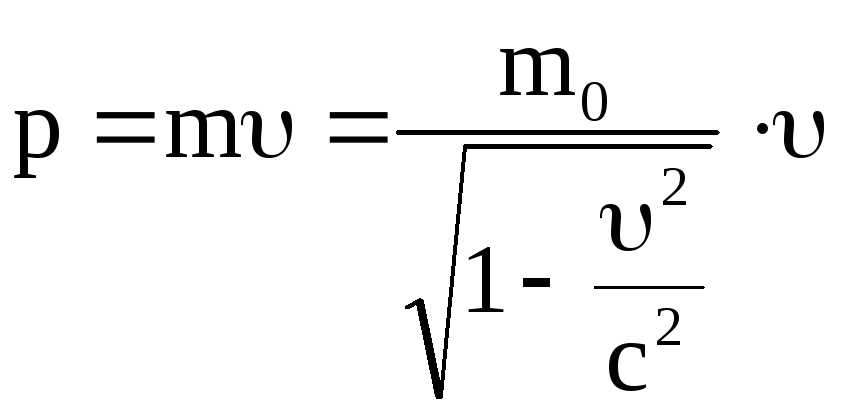Ответ:
E_K

0,66 МэВ; р 
5,6 10^-22
кгм/c.

Соседние файлы в папке Физика лр. Механика

• #
• #
• #
• #

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m1v1 = (m1 + m2)v
Неупругое столкновение движущихся тел	± m1v1 ± m2v2 = ±(m1 + m2)v
В начальный момент система тел неподвижна	0 = m1v’1 – m2v’2
До взаимодействия тела двигались с одинаковой скоростью	(m1 + m2)v = ± m1v’1 ± m2v’2

Сохранение  проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁ + m₂)v

Отсюда скорость равна:

Алиса Никитина | Просмотров: 19.8k