Масса, фундаментальное свойство каждого объекта, измеряет количество вещества, содержащегося в теле. В этом посте будет обсуждаться, как найти массу с помощью ускорения и силы, так как это важно при различных подходах и решаемых задачах.
Сэр Исаак Ньютон предложил ряд принципов и теорий, которые привели к разработке нескольких методов оценки массы объекта. Второй закон Ньютона – самый простой и наиболее широко используемый метод расчета массы, поскольку он включает расчет массы с использованием как силы, так и ускорения.
Давайте посмотрим, как второй закон Ньютона может помочь нам в определении массы любого объекта.
Как найти массу с ускорением и силой, используя Второй закон Ньютона:
Термины масса, сила и ускорение используются в повседневной жизни и связаны друг с другом. Сила — это физическое воздействие, вызывающее состояние движения изменяться, что означает, что оно либо ускоряется, либо замедляется. Масса – это тип сопротивления, который предотвращает изменение состояния объекта под действием силы. В результате объект сможет изменить свое состояние движения, как только сила преодолеет это сопротивление.
Наиболее общая форма Второго закона Ньютона гласит, что сила, действующая на тело или частицу, будет равна скорости изменения импульса тела или частицы. Таким образом, поместив это утверждение в формулу, его можно выразить как:
Где p – линейный импульс объекта. Он рассчитывается как произведение скорости и массы объекта. Таким образом, математически мы можем записать это как:
р = мв
Итак, если значение импульс заменяется силой уравнение, получаем:
Когда скорость объекта приближается к скорости света, масса объекта увеличивается; Тем не менее, это не так. Поскольку скорость оцениваемого объекта не очень велика, т.е. близка к скорости света, масса не изменяется. В результате со временем меняется только скорость, а масса остается постоянной.
Но дифференциация скорости во времени дает ускорение.
В результате сила может быть выражена через массу и ускорение, а ее математическое представление выглядит следующим образом:
F = ма
Второй закон Ньютона представлен этим уравнением. Это можно использовать для расчета массы объекта, задав его уравнение. В результате массу объекта можно рассчитать следующим образом:
Ньютон, килограмм и м / с2 – единицы силы, массы и ускорения в системе СИ, соответственно, согласно Международной системе единиц.
Приведенное выше уравнение масс раскрывает два факта, которые перечислены ниже:
- м ∝ F: – Эта пропорциональность показывает, что большая масса требует большей силы, тогда как меньшая масса требует меньшей силы.
- м ∝ 1 / год: – Поскольку ускорение обратно пропорционально массе объекта, объект с большой массой будет испытывать меньшее ускорение, тогда как объект с низкой массой будет испытывать большее ускорение.
Из этого можно сделать вывод, что если масса объекта велика, для него потребуется большая внешняя сила, а поскольку масса, по сути, является сопротивлением, его ускорение будет законом, и наоборот.
Предположим, вы прилагаете силу и к игрушке, и к настоящей машине. Затем игрушечный автомобиль разгоняется без особых усилий. Однако настоящей машине для движения вперед требуется больше силы. Или, возможно, он вообще не двигается. Это связано с тем, что масса игрушечной машинки меньше, чем у реальной машины. В результате сила, необходимая для их ускорения, варьируется.
Давайте посмотрим на некоторые проблемы нахождения массы с помощью ускорения и силы.
Проблема: когда к объекту прилагается сила в 6.0 ньютонов, он ускоряется со скоростью 12.0 м / с2. Определите массу объекта.
Данный:
Сила на объект F = 6 Н
Ускорение объекта a = 12 м / с2
Найти:
m =?
Решение:
Масса объекта:
∴ м = 2 кг
Таким образом, здесь, в данном случае, масса объекта составляет 2 кг.
Проблема: чтобы разогнать мяч со скоростью 4 м / с2, требуется сила 24 Н. Какой тогда была бы масса объекта?
Данный:
Ускорение мяча a = 4 м / с2
Сила, приложенная к шару F = 24 Н
Найти:
m =?
Решение:
Масса мяча:
∴ м = 6 кг
Таким образом, чтобы разогнаться со скоростью 4 м / с2, мячу весом 6 кг требуется сила 24 Н.
Часто задаваемые вопросы о поиске массы с помощью второго закона Ньютона:
В .: Приведите законы движения Ньютона.
Ответ: Формулировки всех трех законов движения Ньютона приведены ниже:
1-й закон: Состояние тела не изменяется до тех пор, пока на него не перестанет действовать ненулевая результирующая сила, что означает, что если оно неподвижно, оно останется таковым, а если оно движется, оно будет поддерживать свою скорость. Это часто называют законом инерции.
2-й закон: Скорость изменения импульса тела пропорциональна приложенной к нему силе. Или, другими словами, величина ускорения объекта пропорциональна приложенной к нему силе и обратно пропорциональна массе тела. Это можно записать в виде уравнения:
F = ma
3-й закон: Во время взаимодействия двух тел сила, действующая обоими, будет одинаковой по величине и в противоположном направлении.
В: Когда ракета запускается со стартовой площадки, она не только набирает скорость, но и получает огромное ускорение во время стрельбы. Что является причиной этого?
Отв.: Когда ракета запускается, она ускоряется в результате выстрела.
Из-за топлива, используемого в ракетах, стрельба из них возможна. Топливо в ракете горит во время выстрела. В результате постоянной стрельбы масса теряется, а ускорение увеличивается, потому что масса и ускорение обратно пропорциональны.
В: Объясните, как каждый из законов Ньютона влияет на игру в перетягивание каната.
Отв .: Важность каждого закона Ньютона в перетягивании каната указана ниже:
- Первый закон Ньютона: Пока не начнется тяга, то есть пока не будет приложена сила, веревка останется в том же положении.
- Второй закон Ньютона: Силу каждой команды можно рассчитать с помощью второго закона Ньютона. Сила, с которой тянет каждая команда, определяется массой тела каждой команды и ускорением, с которым движется веревка.
- Третий закон Ньютона: Одна команда с силой тянет веревку к себе, а другая тянет веревку от себя. Обе команды, по сути, идут в противоположных направлениях. В результате, пока одна из сторон не достигнет максимума, ни одна из команд не выиграет.
В. Опишите, что произойдет, если вы попытаетесь толкнуть кого-то, кто тяжелее вас. Что, если он тоже оттолкнет вас?
Ответ: Тело будет ускоряться только в том случае, если действующая на него результирующая сила больше нуля.
Поскольку человек, которого вы пытаетесь толкнуть, имеет большую массу, чем вы, ему потребуется больше силы для ускорения, чем вы можете предоставить. В результате человек останется неподвижным. Поскольку ваша масса меньше его, когда он толкает вас назад, вы ускоряетесь в направлении толчка.
Мы видели, как найти массу без ускорения в предыдущем посте, а в этом – как найти массу с ускорением и силой. Мы надеемся, что эти сообщения ответили на ваши вопросы.
Прежде чем отвечать на вопрос о количестве килограммов в одном ньютоне, необходимо разобраться с предложенными понятиями с точки зрения общепринятой системы СИ, учитывая, что ньютон является не столько базовой единицей системы СИ, сколько единицей метрической.
Содержание:
- Порядок решения задачи
- Алгоритм решения вопроса с учетом законов физики
- Формула для перевода величин
Порядок решения задачи
При решении физических задач значения физических величин измерения массы, представленные в единицах, отличных от единиц массы, необходимо перевести в единицы СИ, т. е. в килограммы.
Перевод осуществляем следующим образом:
- 1 Н = 1 кг x 1 м/с2.
Если рассматривать поставленный вопрос буквально, то ответ будет следующим:
- 1 кг/1 Н = 1 кг/(1 кг x 1 м/с2) = 1/(1 м/с2) = 1 с2/м.
Получаем обратную единицу измерения ускорения. В этом нет здравого смысла.
Алгоритм решения вопроса с учетом законов физики
Если рассуждать здраво, то нужно исходить из позиции, что в системе СИ ньютон — единица силы, которую вы получаете при помещении тела в гравитационное поле. Фактически этот показатель используется для обозначения любых сил — гравитационных, электромагнитных, силы трения и других сил с привязкой к массе объекта, на который действуют любые силы. Килограмм же есть единица измерения массы.
Говоря проще, чтобы вытеснить тело весом один килограмм с ускорением один м/с2, нам нужно приложить силу, равную одному ньютону.
Если ограничивать силу только гравитационной силой планетной массы для тела меньшей массы на ее поверхности, можно вывести пропорциональную зависимость между массой и указанной гравитационной силой, приводящей к постоянному ускорению для произвольной массы (пренебрегая другими силами, такими как сопротивление воздуха). Иначе говоря, числовое значение ньютонов в килограмме в любом месте будет равно силе ускорения объекта определенной массы.
Таким образом, в системе СИ значение в 1 Н определяется как сила, необходимая для ускорения массы в один килограмм с ускорением в один метр в секунду за секунду (то есть секунду в квадрате) в направлении действия силы.
Обратите внимание, что сила и ускорение являются векторными величинами, поэтому они имеют направление и величину, тогда как масса — скалярное значение, имеющее только заданную величину.
Сила (F) равна массе (m) раз на ускорение (a): F = m x a .
Такой вывод основан на втором законе ньютоновского движения, ускорение тела, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе этого тела.
Исходя из этого, вопрос о переводе ньютонов в килограммы изначально не имеет никакого смысла. По сути, это равносильно тому, как если бы вы спросили: «Сколько в одном часе метров?» или «Сколько байт в десяти литрах?» Поскольку сравнение различны физических величин, измеряемых в разных единицах, само по себе безосновательно.
Поэтому уместнее было бы рассматривать вопрос о том, как все-таки вычислить, сколько ньютонов в одном килограмме с позиции гравитации в определенном месте на Земле. Иными словами, чтобы найти массу в килограммах, нам нужно знать вес в ньютонах, поскольку масса фактически представляет собой вес тела. Приведя две физические величины с разными значениями к общему знаменателю — в данном случае утверждению о том, что масса равна весу, мы можем смело переводить ньютоны в килограммы и обратно, а также учитывать, насколько сильно гравитационное поле, которое напрямую связано с ускорением.
В частности, мы можем использовать формулу W = m x g (которая, по сути, является особым случаем выражения упомянутого второго закона: F = m x а), где W — вес объекта в ньютонах, m — масса объекта в килограммах, g — гравитационное ускорение объекта в ньютонах на килограмм.
Все по тому же второму закону получаем: F = m x g.
Если предположить, что объект весом 1 кг находится на Земле, поскольку один килограмм веса тяжелее на Земле, чем на Луне или, скажем, на Марсе, то мы учитываем значение g на поверхности Земли, которое составляет g = 9,8 Н/кг. Таким образом, получаем: W = 9,8 * 1 = 9,8 Н, то есть один килограмм составляет 9,8 ньютонов. Таким образом, мы с вами осуществили перевод килограммов в ньютоны:
Тело весом один килограмм имеет (стандартный) вес равный 9,8 Н.
Идем дальше. «Стандартная гравитация» или «стандартное ускорение свободного падения» (g ₀) составляет 9,80665 м/с² или 9,80665 Н/кг — среднее значение гравитации на поверхности планеты Земля.
Несмотря на то, что это значение является общепринятым для преобразования значений между массой и силой тяжести, это теоретическое значение, поскольку справедливо оно только для некоторых мест на Земле вблизи уровня моря.
Фактическая же сила тяжести на Земле изменяется на 0,7%. Но это частности. Хотя, как известно, из-за того, что не учитываются исключения и частности, могут возникать неточности при проведении измерений.
Формула для перевода величин
Отвечая на вопрос о переводе ньютонов в килограммы при стандартной гравитации (и это важно), получаем следующее значение:
- 1 Н ÷ g ₀ ≃ 0,101972 кг.
Округлив полученное значение, можно записать следующее:
- 1 Н = 0,101 кг.
Загрузить PDF
Загрузить PDF
Масса – это количество материи, содержащейся в данном теле. Материя – это все, что можно физически ощутить. В большинстве случаев масса зависит от размеров тела, но это не всегда так – например, размеры воздушного шара могут быть больше размеров определенного тела, но при этом масса шара будет меньше массы этого тела. Эта статья расскажет вам, как найти массу.
-
1
Используйте трехрычажные весы. Любые весы используются для нахождения массы тел. В рассматриваемых весах есть три рычага, на каждом из которых имеется передвижная гиря.[1]
Также каждый рычаг снабжен шкалой, вдоль которой двигается гиря определенной массы.[2]
- На показания трехрычажных весов не влияет сила тяжести, что позволяет произвести точные измерения массы. В таких весах неизвестная масса сравнивается с известной массой.
- Средняя шкала имеет шаг 100 г. Дальняя шкала имеет шаг 10 г. Ближняя шкала измеряет вес в диапазоне 0-10 г.
- При помощи трехрычажных весов можно произвести очень точные измерения массы тела. В случае использования таких весов ошибка измерения составит всего 0,06 г. Принцип работы таких весов похож на принцип работы детской карусели.[3]
-
2
Передвиньте гири в крайнее левое положений. Это нужно сделать тогда, когда чаша весов пустая. В этом случае весы будут показывать 0.
- Если индикатор, расположенный справа, не совпадает с фиксированной меткой, откалибруйте весы, поворачивая калибровочный винт (он находится слева под чашей весов).
- Калибруют весы для того, чтобы масса чаши не влияла на показания весов, то есть когда чаша пустая, весы должны показывать 0 г. Масса чаши называется весом тары.
- Для того чтобы с чашей весы показывали 0 г, покрутите калибровочный винт, расположенный под чашей. Затем положите на чашу предмет (тело), массу которого вы хотите найти (это делается при помощи передвижных гирь).
-
3
Двигайте гири по одной. Для начала передвиньте гирю по средней шкале (с шагом 100 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число сотен граммов. За один раз передвигайте гирю на одно деление.
- Затем передвиньте гирю по дальней шкале (с шагом 10 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число десятков граммов.
- Ближняя шкала делений не имеет. Вы можете перемещать гирю по ней в любом направлении. Числа на этой шкале обозначают граммы, а штриховые метки между числами – десятые грамма.
-
4
Найдите массу тела. Теперь вы можете определить массу тела, находящегося на чаше весов. Для этого сложите показания трех шкал.
- Показания каждой шкалы читаются аналогично показаниям линейки. При этом учитывают показания до ближайшей середины между делениями.
- Например, измерим массу банки с содовой. Если дальняя шкала показывает 70 г, средняя шкала показывает 300 г, а ближняя шкала показывает 3,34 г, то масса банки равна 373,34 г.
Реклама
-
1
Вычисление массы через объем и плотность. Формула для вычисления плотности: плотность = масса / объем. Для того чтобы воспользоваться этой формулой, вам нужно знать объем и плотность тела.[4]
- Согласно этой формуле масса тела равна произведению плотности на объем: масса = объем Х плотность. Например, объем алмаза равен 0,00500 кубическим метрам, а его плотность равна 3,520 кгм^3. Для вычисления массы алмаза перемножьте эти значения: 0,00500 Х 3,520.
- Для перемножения значений воспользуйтесь онлайн-калькулятором. Его можно найти на разных сайтах.[5]
[6]
- Вы можете воспользоваться специальным калькулятором для вычисления объема тела. Например, вы можете найти объем конуса, если вам известны радиус его основания и высота.[7]
-
2
Уясните разницу между массой и весом. Это разные величины. Масса – это количество материи, содержащейся в данном теле. Вес – это сила, с которой тело действует на опору и которая возникает в поле силы тяжести. Вес тела возрастает с увеличением его массы.
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
Не забудьте вычислить массу тела в соответствующих единицах измерения (килограммах и граммах), а для обозначения массы используйте специальный символ (букву латинского алфавита). - Вес тел одинаковой массы может быть различным (в зависимости от силы тяжести). Например вес тела на Земле будет отличаться от веса того же тела на Луне.[9]
- Не измеряйте массу тела в фунтах и унциях.[10]
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
-
3
Вычисление массы через силу и ускорение. Формула для вычисление силы: F = m Х a.
- Таким образом, формула для вычисления массы: m = F/a, то есть масса равна силе, деленной на ускорение. Масса тела присутствует в формулировке второго закона Ньютона, который гласит, что ускорение прямо пропорционально вызывающей его силе и обратно пропорционально массе тела.
- Масса измеряется в килограммах (кг). Сила измеряется в ньютонах (Н).[11]
Реклама
Советы
- Масса обозначается буквой m. Масса считается постоянной величиной.
Реклама
Об этой статье
Эту страницу просматривали 19 820 раз.
Была ли эта статья полезной?
Содержание:
- Масса
- Второй закон Ньютона
- Масса — мера инертности тела
- Система единиц измерения механических величин
- Примеры решения задач на второй закон Ньютона
Масса – это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Масса
Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.
Массой тела называется количество вещества, содержащегося в этом теле.
Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.
Рис. 98. Измерение массы тела.
Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.
За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.
В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).
В практике эталоны масс изготовляют в виде гирь различной величины.
Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.
Второй закон Ньютона
Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.
Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.
Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле 
определяем ускорение а.
Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.
Результаты таких измерений и вычислений отражены в таблице.
Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.
Математически это можно записать в виде формулы:
Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.
Нагружая тележку гирями, изменим массу движущихся тел.
Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.
Результаты опытов снова занесём в таблицу.
Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:
Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.
Кроме того, ускорение тела совпадает с этой силой по направлению.
Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.
Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.
Второй закон Ньютона математически можно выразить в виде следующей формулы:
откуда 
Величина силы равна произведению массы тела на ускорение.
Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.
В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:
Р = mg.
Из сопоставления формулы F=ma и P=mg видно, что
т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.
При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.
Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением 
Определить силу, движущую санки.
Р=70 кГ;
g=
а =
F = ?
Из формулы 
определим F:
Масса — мера инертности тела
Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.
Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.
Рис. 100. Масса наковальни значительно больше массы молота.
Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона 
т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.
Итак, масса тела является мерой его инертности.
Из второго закона Ньютона 
следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.
Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.
Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.
Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.
Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.
Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.
Рис. 101. Машина на массивном фундаменте.
Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.
Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:
Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.
Система единиц измерения механических величин
Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.
Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в 
Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.
Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.
В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( 
средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).
Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).
Единица скорости в этой системе 
единица ускорения 
Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:
За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным 
Эта единица называется диной (сокращённо дн).
В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:
единица длины — 1 м,
единица массы — 1 кг,
единица времени — 1 сек,
единица тока — 1 ампер.
Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).
Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением 
Эта единица называется ньютон (сокращённо н). Таким образом,
Вычислим, сколько в одном ньютоне содержится дин.
или 
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:
единица длины —1 м,
единица силы —1 кГ,
единица времени—1 сек.
Единица массы в этой системе единиц является производной и может быть определена из равенства 
т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением 
Сокращённое обозначение этой единицы—т. е. м. Таким образом,
Между различными единицами массы и силы существуют следующие соотношения:
1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение 
Отсюда: 
или округлённо:
Так как 
то 1 кГ = 9,8 н.
Примеры решения задач на второй закон Ньютона
1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?
Расчёты ведём в системе CGS.
Дано: F = 2 кГ=2*980000 дн = 1960000 дн;
m=19600 г; t = 5 сек. Найти 
Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:
Время t дано по условиям задачи.
Ускорение найдем на основании второго закона: 
Ответ: 
2. Тело весом 98 кГ движется со скоростью, равной 
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.
Дано: Р = 98 кГ; 
t = 300 сек. Найти F.
Искомую силу найдём на основании второго закона:
F = mа.
Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;
Так как 
то
и 
По второму закону Ньютона Р = mg, откуда
Ответ. 
3. На тело, движущееся с начальной скоростью в 
подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.
Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:
Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, 
ускорение а по условиям задачи вычислим по формуле:
откуда
Масса тела
Ответ. 
При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.
Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.
Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.
Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.
m = 10 г; t = 60 сек.; s = 1800 см.
По второму закону Ньютона F = ma. (1)
Масса дана, ускорение а находим по формуле пути равноускоренного движения: 
откуда
Подставим значение а из равенства (2) в равенство (1), получим:
Подставляя численные значения величин в равенство (3), определим величину силы F:
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Содержание:
- Определение и формула массы тела
- Инертная масса
- Гравитационная масса
- Формула расчета массы через плотность тела
- Масса в специальной теории относительности
- Примеры решения задач
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (mi):
$$m=sum_{i=1}^{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$bar{F}=m bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (Ft) избранного тела:
$$m=frac{F_{t}}{g}(3)$$
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
$$m=int_{V} rho d V(4)$$
где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:
$m = rho V (5)$
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Примеры решения задач
Пример
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.
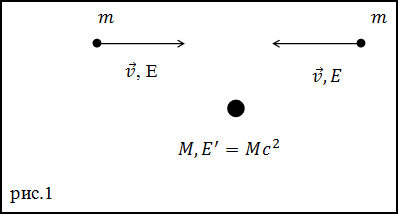
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
$$E^{prime}=M c^{2}(1.1)$$
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
