С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
На данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
Что представляет собой рычаг?
Рычаг — это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
На камень действует сила — вес $P$. Для того чтобы поднять камень, необходимо преодолеть его вес, направленный вертикально вниз. В первом случае (рисунок 2, а) Образавр давит на конец палки с силой $F$, а во втором (рисунок 2, б) — поднимает конец палки.
В обоих случаях у этого рычага есть неподвижная точка опоры — точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг), меньше веса камня, но тем не менее у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Виды рычагов
Таким образом, рычаги бывают двух видов (рисунок 3):
- Рычаг 1-го рода — силы приложены по разные стороны от точки опоры O (рисунок 3, а);
- Рычаг 2-го рода — силы приложены по одну сторону от точки опоры O (рисунок 3, б).
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Плечо силы рычага
На рисунке 4 изображен рычаг. Его точки A и B — это точки приложения сил $F_1$ и $F_2$ соответственно. Точка опоры O расположена между точками A и B — значит, перед нами рычаг 1-го рода.
А теперь взгляните на схему этого рычага (рисунок 4). Силы $F_1$ и $F_2$ направлены в одну сторону.
Длина отрезка OA обозначена как $l_1$, а длина отрезка OB — $l_2$. Эти величины называются плечом силы.
Что называют плечом силы?
Плечо силы — это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Как найти плечо силы?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
Тогда, OA или $l_1$ — это плечо силы $F_1$, а OB или $l_2$ — плечо силы $F_2$.
Условие равновесия рычага
Чтобы получить условие равновесия рычага, нужно провести опыты. К рычагу по обе стороны от точки опоры подвешиваются разные груза так, чтобы каждый раз рычаг оставался в равновесии. В каждом случае измеряются модули сил и их плечи. В нашем случае (рисунок 4) видно, что сила $2 space Н$ уравновешивает силу $4 space Н$. А плечо меньшей силы в 2 раза больше плеча большей силы.
С помощью таких опытов было установлено правило равновесия рычага.
В чем состоит правило равновесия рычага?
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:
$frac{F_1}{F_2} = frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, которые действуют на рычаг, $l_1$ и $l_2$ — плечи этих сил.
Кто установил правило равновесия рычага?
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют — правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: «Дайте мне точку опору, и я переверну Землю!».
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Например, возьмем рычаг, у которого одно плечо будет в 2 раза больше другого (как на рисунке 4). Приложим к точке A силу в $100 space Н$. Тогда в точке B мы сможем уравновесить силу в $200 space Н$ (в 2 раза большую). Если нам нужно поднять более тяжелый груз, то можно увеличить плечо рычага $l_1$, к которому мы прикладываем силу.
Примеры задач
Задача №1
Рабочий поднимает груз массой $300 space кг$ c помощью рычага 1-го рода. Большее плечо силы рано $3 space м$, а меньшее — $0.6 space м$. Какую силу рабочий прикладывает к большему плечу рычага?
Дано:
$m = 300 space кг$
$l_1 = 3 space м$
$l_2 = 0.6 space м$
$g = 9.8 frac{Н}{кг}$
$F_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда силу $F_1$, которую прикладывает к рычагу рабочий:
$F_1 = F_2 cdot frac{l_2}{l_1}$.
Сила $F_2$ — это вес груза $P$, который мы можем рассчитать формуле: $P = gm$. Подставим в нашу формулу и рассчитаем силу $F_1$:
$F_1 = F_2 cdot frac{l_2}{l_1} = gm cdot frac{l_2}{l_1} = 9.8 frac{Н}{кг} cdot 300 space кг cdot frac{0.6 space м}{3 space м} = 2940 space Н cdot 0.2 = 588 space Н$.
Ответ: $F_1 = 588 space Н$.
Задача №2
На рисунке 7 схематически изображен рычаг. Точка опоры находится в точке O. Одно деление на шкале рычага равно $10 space см$. Какую массу должен иметь груз, подвешенный в точке A, чтобы рычаг находился в равновесии?
Дано:
$m_1 = 100 space г$
$m_2 = 200 space г$
$l_1 = 50 space см$
$l_2 = 20 space см$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_1 = 0.1 space кг$
$m_2 = 0.2 space кг$
$l_1 = 0.5 space м$
$l_2 = 0.2 space м$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем силу, которая будет действовать на рычаг в точке B. Эта сила будет равна весу $P_2$, с которым груза массой $m_1$ и $m_2$ действуют на подвес. Обозначим эту силу $F_2$.
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 frac{Н}{кг} cdot (0.1 space кг + 0.2 space кг) = 9.8 frac{Н}{кг} cdot 0.3 space кг approx 3 space Н$.
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда и рассчитаем силу $F_1$, с которой будет действовать на рычаг груз неизвестной массы:
$F_1 = frac{F_2 cdot l_2}{l_1} = frac{3 space Н cdot 0.2 space м}{0.5 space м} = 1.2 space Н$.
Сила $F_1$ будет равна весу $P_1$, с которым груз массой $m_3$ действуют на подвес:
$F_1 = P_1 = gm_3$.
Найдем массу груза:
$m_3 = frac{F_1}{g} = frac{1.2 space Н}{9.8 frac{Н}{кг}} approx 0.1 space кг = 100 space г$.
Ответ: $m_3 = 100 space г$.
Как найти нагрузку на точку опоры у рычага?
Ученик
(245),
на голосовании
9 лет назад
Голосование за лучший ответ
Иван Федоров
Просветленный
(41602)
9 лет назад
А чего инет рыть? Тут все просто: рычаг – это “весы”. В простейшем случае сила тяжести камня уравновешена силой, приложенной к другому концу рычага (весом самого рычага пренебрегаем, камень поднимаем равномерно, без ускорения) . Обе эти силы направлены вниз (т. е. в одну сторону) и уравновешены силой реакции опоры рычага (система неподвижна) . А раз силы, приложенные к концам рычага, направлены в одну сторону, то они складываются. Вот и получается, что нагрузка на точку опоры рычага равна сумме сил, т. е. в Вашем примере эквивалентна нагрузке от тела массой 210 кг.
Рычаги
«Дайте мне точку опоры, и я переверну Землю!»
Архимед
В данной теме речь пойдёт о простых механизмах, используемых человечеством с незапамятных времен, и более подробно остановимся на самом распространенном из них — рычаге.
Ранее говорилось о механической работы и мощности. Механическая работа — это скалярная физическая величина, пропорциональная приложенной к телу силе и пройденному телом пути. Единицей работы в системе СИ является Дж (джоуль). Мощность — это скалярная физическая величина, которая характеризует быстроту совершения работы. Единицей мощности в системе СИ является Вт (ватт).
С незапамятных времен человечество использует различные приспособления для совершения механической работы. Известно, что очень тяжелые предметы достаточно трудно, а временами и невозможно, передвинуть непосредственно. Однако используя достаточно длинную палку, или, как ее еще называют, рычаг, это можем сделать достаточно легко.
Если посетить любое современное производство, то можно увидеть, как работают машины. Они, как разумные существа, прессуют, гнут, режут большие металлические листы, считают и сортируют, взвешивают и упаковывают различные изделия.
Однако если рассмотреть любое устройство такой сложной конструкции, то можно заметить, что ее механическая составляющая представлена сочетаниями всего шести видов простых механизмов — рычагов, блоков, винтов, клиньев, воротов и наклонных плоскостей.
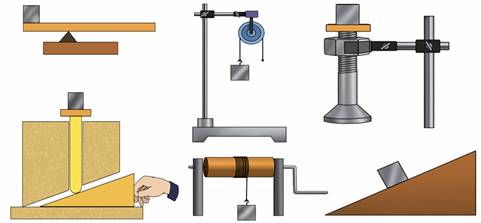
В быту также часто используются простые механизмы — это топор, лопата, ножницы, мясорубка и многое другое.
Зачем нам нужны простые механизмы? Для ответа на этот вопрос, рассмотрим простой пример. Пусть необходимо поднять груз на некоторую высоту. Для этого можно воспользоваться одним из шести простых механизмов. Во всех шести случаях действие силы приведет к подъему тела. Но эта сила вовсе не направлена вверх и, за исключением одного случая, не приложена непосредственно к поднимаемому телу. Но самое важное здесь то, что эта сила во всех случаях меньше веса поднимаемого тела. Значит, использование простых механизмов позволяет получить выигрыш в силе.
Таким образом, простые механизмы — это приспособления, которые служат для преобразования силы.
Но простые механизмы служат не только для подъема тела. Их используют, когда режут ножницами бумагу или ткань, колют дрова, гребут веслами и т. д. Более того, эти механизмы есть и в теле человека.
Простые механизмы использовались человеком с древнейших времен. Воображение каждого туриста, посетившего остров Пасхи, поражают древние каменные изваяния огромных размеров, расположенные по всему острову. В создании этих тяжелых каменных изваяний (а на одном из них только шляпа имеет массу около 3 т), при их подъеме в вертикальное положение использовались простые механизмы. Аналогично строились и великие египетские пирамиды.
Одним из наиболее распространенных простых механизмов является рычаг. Именно он позволяет малой силой уравновесить большую силу. Рычаги присутствуют во многих устройствах.
Что же такое рычаг и как получить выигрыш в силе, пользуясь им? Рычагом является любое твердое тело, которое может поворачиваться относительно неподвижной оси или опоры. Все рычаги делятся на 2 вида: рычаг первого рода и второго рода.
Рычагом первого рода называется рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Примером могут служить ножницы, коромысло равноплечих весов и др.
Рычагом второго рода называется рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу. Это, например, гаечные ключи, двери и т.д.
При каких условиях рычаг находится в равновесии? Поставим опыт. (Сразу отметим, что все выводы, которые будут сделаны нами для рычага первого рода, будут справедливы и для рычага второго рода). Возьмем в качестве рычага линейку длиной 1 метр, и поместим ее на неподвижную опору, находящуюся ровно посередине. На расстоянии 0,25 м от опоры поставим гирю весом 8 Н. Естественно, конец рычага под действием веса гири опустится. Теперь надавим на свободный конец рычага динамометром и поднимем гирю так, чтобы рычаг установился горизонтально. При этом динамометр покажет силу, равную 4 Н.
Так почему же неравные силы, которые приложены к рычагу, удерживают его в равновесии? Все потому, что результат действия силы на рычаг определяется не только ее модулем, но и расстоянием от точки опоры до линии действия силы.
Расстояние от точки опоры до прямой, вдоль которой действует сила, называется плечом этой силы.
Рассмотрим схему данного опыта.
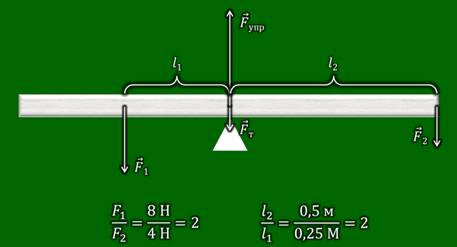
Кроме сил F1 и F2, плечи которых обозначены, как l1 и l2, на рычаг будут действовать еще две силы — сила тяжести рычага и сила упругости опоры.
Как видно из рисунка, плечи этих сил равны нулю, поэтому на равновесие рычага они не влияют. Теперь сравним силы F1 и F2 и их плечи. Сила F2 в два раза меньше силы F1, а плечо силы F2 в два раза больше плеча силы F1.
Что произойдет, если плечо силы F2 увеличить, скажем, в 5 или 25 раз? То и сила уменьшилась бы в 5 или 25 раз. Т.е., чем больше плечо, тем меньше сила, с помощью которой можно поднять груз, лежащий на противоположной от опоры части рычага.
Первое письменное объяснение равновесия рычага было дано в третьем веке до нашей эры древнегреческим ученым Архимедом, который впервые смог связать понятия силы, груза и плеча. Закон равновесия, сформулированный Архимедом, до сих пор используется и звучит так: рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.
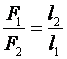– условие равновесия рычага
По легенде, осознав значимость своего открытия, Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!». Правда, сделать это при своей жизни Архимед бы не смог. Да и сейчас тоже. Все дело в том, что для поднятия нашей планеты хотя бы на один сантиметр, требуется неимоверно длинный рычаг, который пришлось бы двигать в течение нескольких десятков миллионов лет со скоростью 1 см в минуту.
Упражнения.
Задача 1. На одном конце линейки длиной 100 см подвешена гиря массой 500 г. Посередине линейки снизу находится опора, относительно которой линейка может свободно поворачиваться. Где надо подвесить второй груз массой 750 г, чтобы линейка находилась в равновесии?
Задача 2. На концах легкого стержня длиной 32 см подвешены грузы массами 40 г и 120 г. Где нужно подпереть стержень, чтобы он находился в равновесии?
Основные выводы:
– Простые механизмы, служат для преобразования механического действия на тело, позволяя изменить точку приложения силы, ее модуль и направление.
– Простые механизмы, как рычаг, блок, ворот, клин, наклонная плоскость и винт являются составными частями конструкций любых механических устройств.
– Рычаг – это любое твердое тело, которое может поворачиваться относительно неподвижной опоры или оси.
– Рычаги делятся на два вида — рычаг первого и рычаг второго рода.
– Рычагом первого рода называется рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону.
– Рычагом второго рода называется рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу.
– Плечо силы – это расстояние от точки опоры до прямой, вдоль которой действует сила.
– Условие равновесия рычага: рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.
– Рычаг дает выигрыш в силе во столько раз, во сколько раз плечо прилагаемой силы больше плеча веса удерживаемого груза.
Домашняя работа
Стр. 170 — 175 читать
Момент силы. Задачи на рычаги.
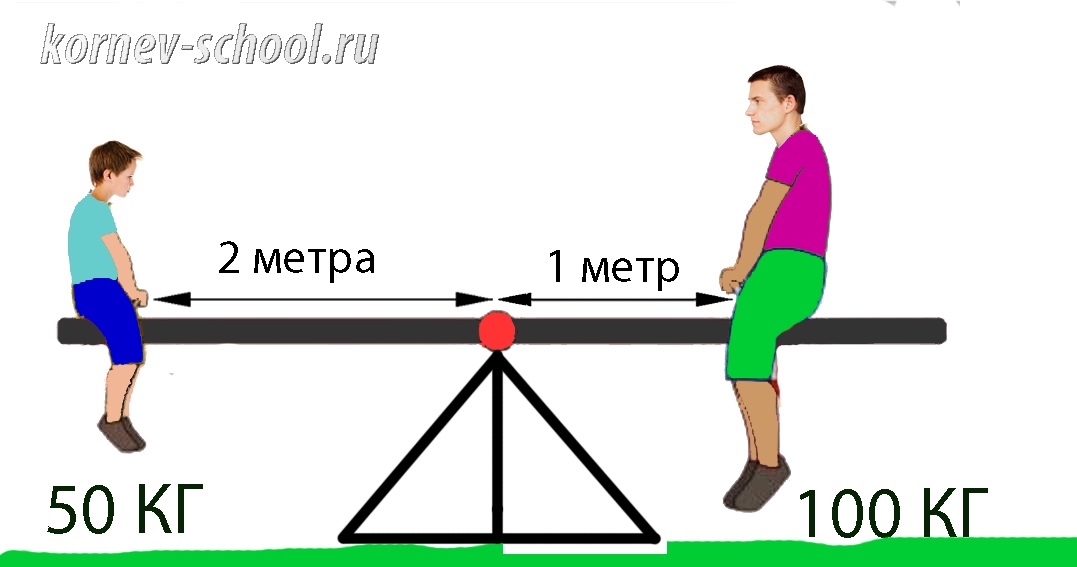
Почему легкий мальчик и взрослый тяжелый мужчина уравновешивают друг друга?
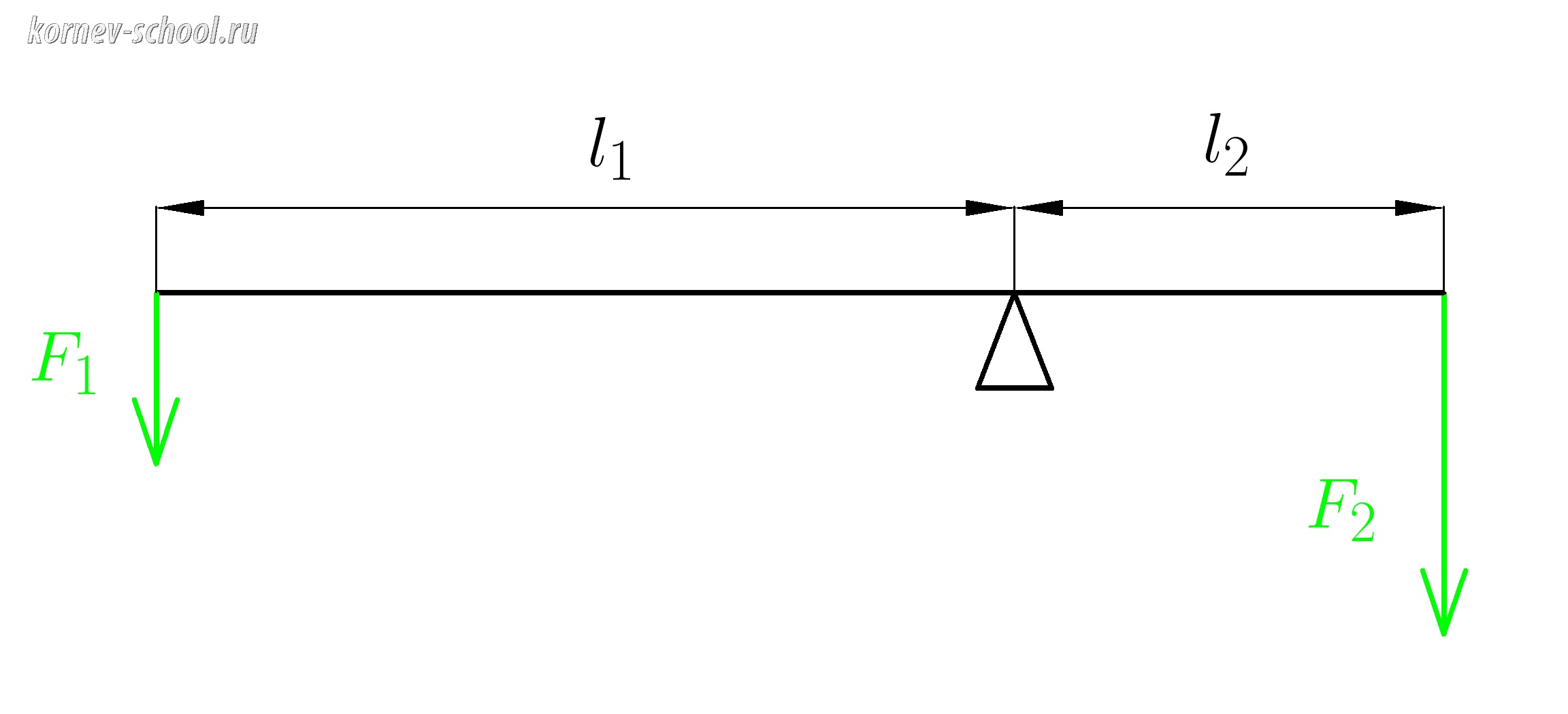
Условие равновесия рычага:
(F_1l_1=F_2l_2)
Для решения простейших задач на рычаги достаточно того, что написано выше
Ниже будет приведено подробное объяснение.
Репетитор по физике
8 916 478 10 32
Плечом силы называют кратчайшее расстояние между линией действия силы и точкой опоры.
( l_1 ) – плечо силы (F_1 ;;;;; ) ( ;;; l_2 ) – плечо силы (F_2 )
Моментом силы называют произведение (умножение) силы на ее плечо:
(M=Fl) .
Момент силы ( F_1 ) пытается закрутить рычаг против часовой стрелки
Момент силы ( F_2 ) пытается закрутить рычаг по часовой стрелке
Условие равновесия:
Рычаг будет находиться в равновесии если сумма моментов, закручивающих его по часовой стрелке будет равна
сумме моментов, закручивающих его против часовой стрелки.
На нашем рисунке один момент закручивает рычаг по часовой,а другой против часовой стрелки, по этому
условие равновесия для нашего случая выглядит вот так:
(M_1=M_2 )
(F_1l_1=F_2l_2)
Задача 1.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_2=100Н ) , плечо этой силы (l_2=2м).
Найти силу (F_1) , если ее плечо (l_1=4м).
Показать ответ
Показать решение
Видеорешение
Задача 2.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_2=6Н ) , плечо этой силы (l_2=0,8м).
Найти силу (F_1) , если ее плечо (l_1=1,6м).
Показать ответ
Показать решение
Видеорешение
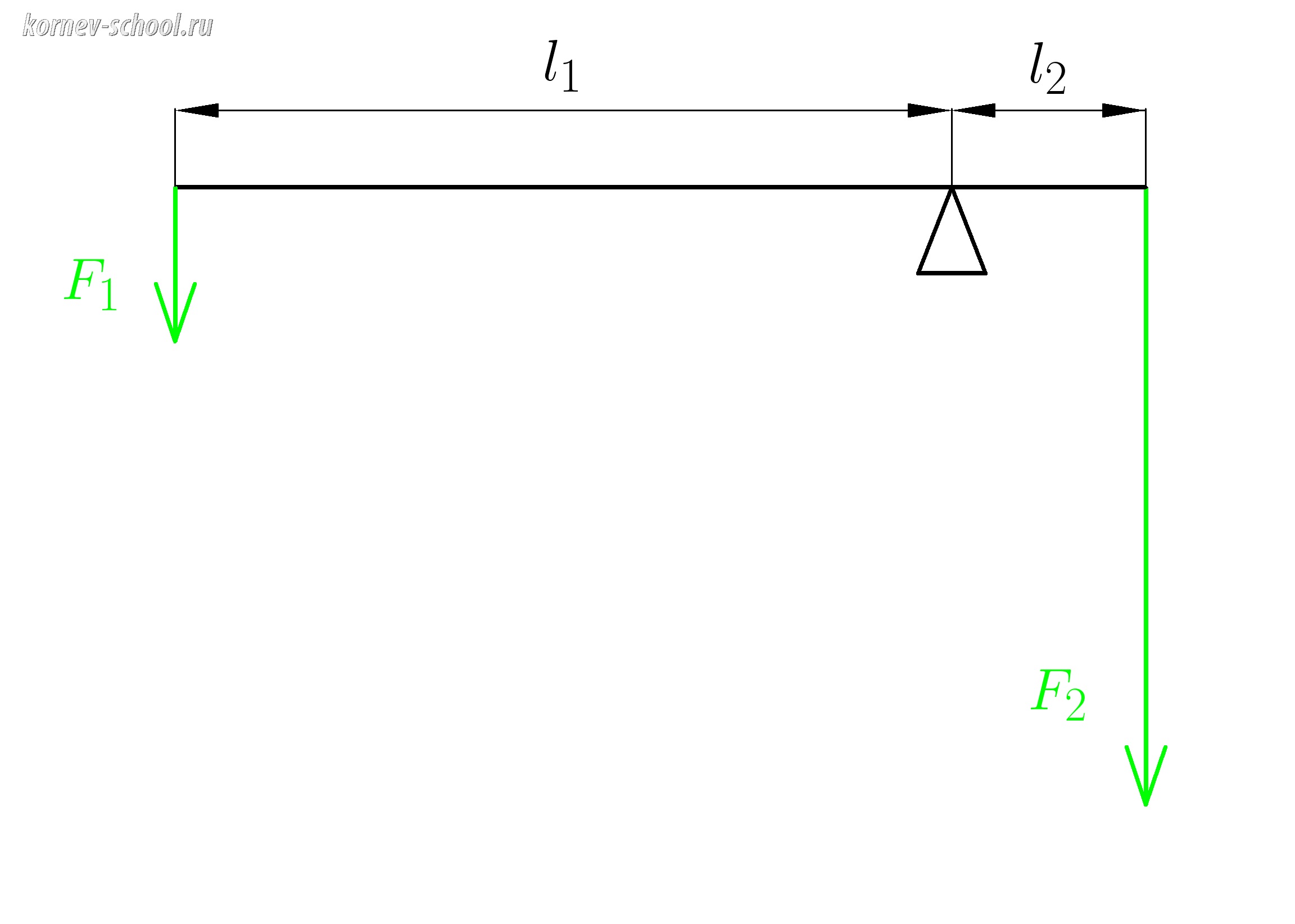
Задача 3.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_1=70Н ) , плечо этой силы (l_1=6м).
Найти силу (F_2) , если ее плечо (l_2=1,5м).
Показать ответ
Показать решение
Видеорешение
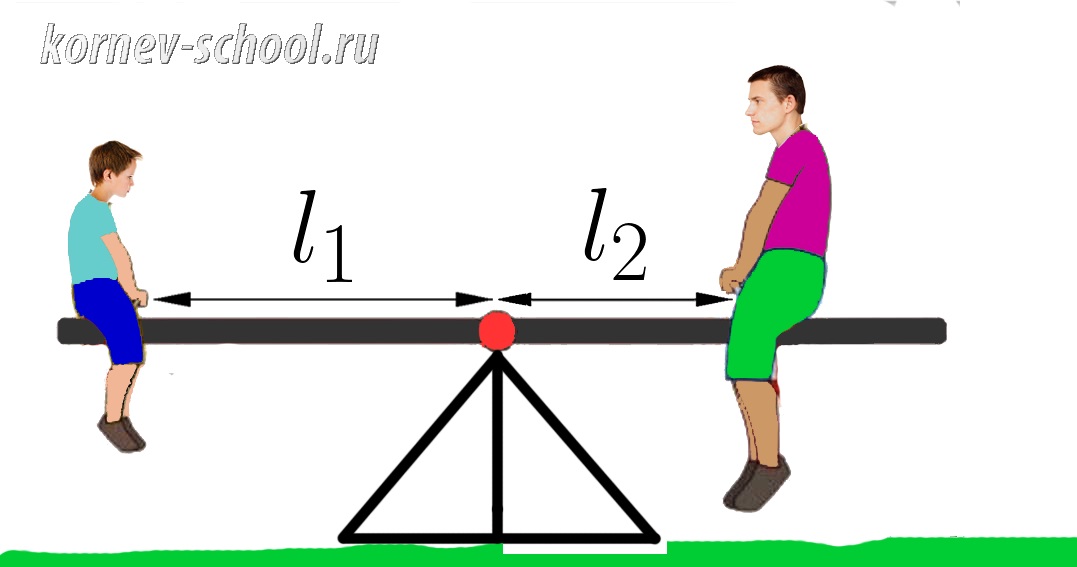
Задача 5.
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 80 килограмм, при этом он сидит на расстоянии (l_2=0,9 м ) от точки опоры качелей.
Найти массу сына, если он сидит на расстоянии (l_1=1,8 м ) от точки опоры качелей.
Показать ответ
Показать решение
Видеорешение
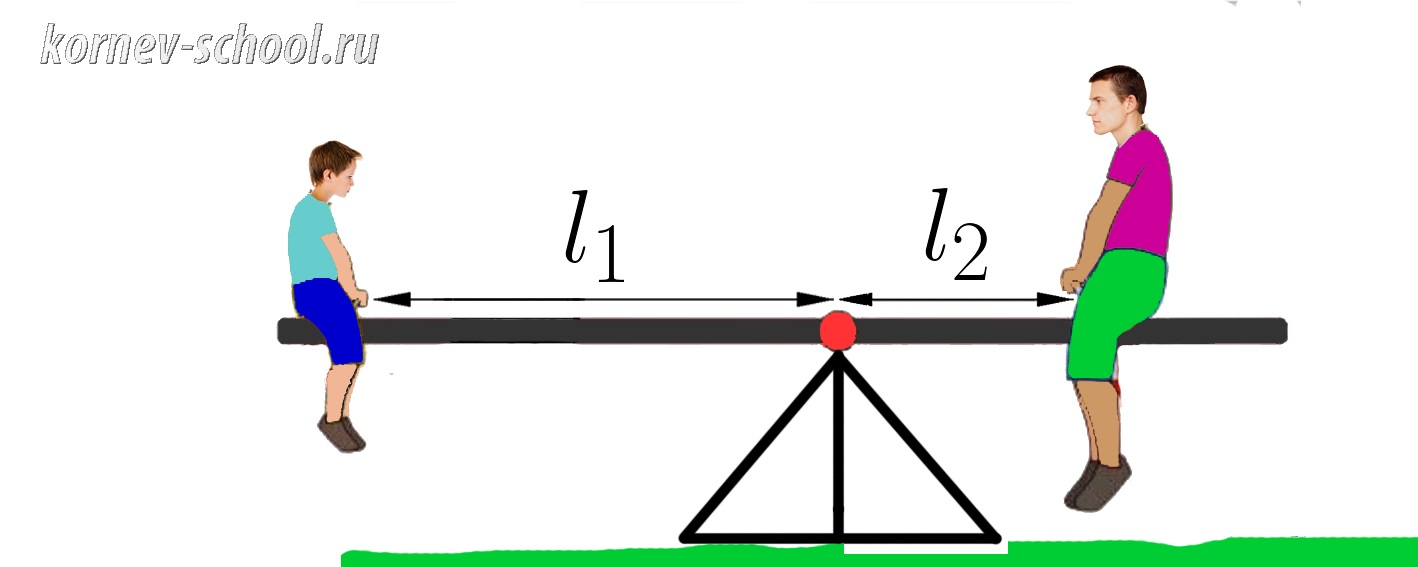
Задача 6.
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 90 килограмм, при этом он сидит на расстоянии (l_2=0,7 м ) от точки опоры качелей.
На каком расстоянии от точки опоры сидит ребенок, если его масса составляет 30 килограмм ?
Показать ответ
Показать решение
Видеорешение
Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке (l_1) – плечо силы (F_1, l_2) – плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) – по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы – Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) – по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы. 
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)
Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
|
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) – правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) – правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
