Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Спрятать решение
Решение.
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение:
Значит, масса первого сплава равна 6 кг, тогда масса второго сплава равна 10 кг и масса третьего сплава равна 16 кг.
Ответ: 16 кг.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Ход решения задачи верный, получен верный ответ | 2 |
| Ход решения правильный, все его шаги присутствуют, но допущена ошибка или описка вычислительного характера | 1 |
| Другие случаи, не соответствующие указанным критериям | 0 |
| Максимальный балл | 2 |
Из двух сплавов получили третий
Из двух сплавов получили третий — ещё один вид заданий 22 и 11 ОГЭ и ЕГЭ по математике.
Задача 1
Первый сплав содержит 15% меди, второй — 40% меди. Масса второго сплава больше массы первого на 45 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава.
Решение:
Пусть масса первого сплава равна x кг, тогда масса второго равна (x+45) кг, а масса третьего — (x+x+45)=(2x+45) кг.
Так как первый сплав 15-процентный, то в x кг этого сплава содержится 0,15x кг меди.
Так как второй сплав 40-процентный, то в x кг этого сплава содержится 0,4(x+45) кг меди.
Так как третий сплав 35-процентный, то в x кг этого сплава содержится 0,35(2x+45) кг меди.
Эти рассуждения наглядно отображены в таблице:
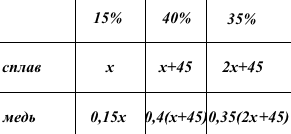
Составим уравнение и решим его:
0,15x+0,4(x+45)= 0,35(2x+45)
Для упрощения вычислений умножим обе части уравнения на 100:
15x+40(x+45)= 35(2x+45)
15x+40x+1800= 70x+1575
-15x=-225
x=15
Масса третьего сплава равна 2·15+45=75 кг.
Ответ: 75 кг.
Задача 2
Имеется два сплава. Первый содержит 20% никеля, второй — 45% никеля. Из этих двух сплавов получили третий сплав массой 90 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была больше массы второго?
Решение:
Пусть масса первого сплава равна x кг, тогда масса второго сплава равна (90-x) кг.
Так как первый сплав 20-процентный, то в x кг этого сплава содержится 0,2x кг никеля.
Так как второй сплав 45-процентный, то в x кг этого сплава содержится 0,45(90-x) кг никеля.
Так как первый сплав 20-процентный, то в x кг этого сплава содержится 0,3·90=27 кг никеля.
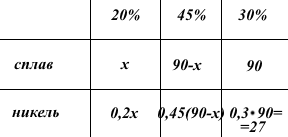
Составим уравнение и решим его:
0,2x+0,45(90-x)=27 ¦·100
20x+45(90-x)=2700
20x+4050-45x=2700
-25x=-1350
x=54
Масса первого сплава 54 кг, масса второго 90-54=36 кг.
Масса первого больше массы второго на 54-36=18 кг.
Ответ: на 18 кг.
При решении задач на сплавы и смеси считают, что сумма масс сплавляемых веществ равна массе получаемого сплава, что сумма масс вещества, входящего в сплавы равна массе этого вещества в полученном сплаве. Аналогичное допущение принимаем и для сумм масс (объёмов) при смешивании жидкостей.
Рассмотрим подготовительную задачу.
Задача 1. Имеется уксусный раствор массой 1,5 кг, содержащий 40 % уксуса. Сколько килограммов воды нужно добавить в раствор, чтобы новый раствор содержал 10 % уксуса?
Решение. I способ.
1) 40 : 10 = 4 (раза) — во столько раз уменьшилась концентрация уксуса в растворе и увеличилась масса раствора,
2) 1,5 * 4 = 6 (кг) — масса нового раствора,
3) 6 – 1,5 = 4,5 (кг) — воды надо добавить.
II способ. 1) 0,4 * 1,5 = 0,6 (кг) — масса уксуса в первом растворе.
2) Пусть добавили x кг воды. Составим уравнение:
0,1(1,5 + x) = 0,6.
Оно имеет единственный корень 4,5. Значит, надо добавить 4,5 кг воды.
Ответ. 4,5 кг.
Рассмотрим способы решения задач на смеси и сплавы из сборников вариантов для подготовки к ЕГЭ.
Задача 2. (2017) В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
Задача 3. (2018) Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение. Пусть масса первого сплава x кг, второго (150 – x) кг, третьего — 150 кг. Найдём массу никеля в каждом из трёх сплавов. Никеля было
в первом сплаве 0,25x кг,
во втором — 0,3(150 – x) кг,
в третьем — 0,28 *150 = 42 (кг).
Составим уравнение:
0,25x + 0,3(150 – x) = 42.
Решив уравнение, получим его единственный корень x = 60. Теперь ответим на вопрос задачи. Масса первого сплава 60 кг, масса второго сплава 90 кг, первая меньше второй на 30 кг.
Ответ. На 30 кг.
Задача 4. (2019) Первый сплав содержит 5 % меди, второй — 14 % меди. Масса второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Решив уравнение, получим его единственный корень x = 28. При x = 28 масса третьего сплава 2x + 7 равна 63 кг.
Ответ. 63 кг.
Задача 5. (2017) Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?
Решение. Пусть масса первого раствора x кг, второго y кг. Приравняв массы кислоты до смешивания и после смешивания, составим два уравнения:
0,7x + 0,6y = 0,5(x + y + 2),
0,7x + 0,6y + 0,9*2 = 0,7(x + y + 2).
Решив систему этих двух уравнений, получим её единственное решение:
x = 3, y = 4. Использовали 3 кг 70 %-го раствора кислоты.
Ответ. 3 кг.
Задача 6. (2017) Имеется два сосуда. Первый содержит 100 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 28 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Для второго смешивания возьмём 1 кг первого раствора и 1 кг второго, получим 2 кг смеси. Составим первое уравнение:
Решив систему уравнений (1) и (2), получим её единственное решение: x = 12, y = 60. В первом сосуде содержится x * 100 / 100 = 12 (кг) кислоты. Ответ. 12 кг.
Для самостоятельного решения
7. Имеется 400 г морской воды, содержащей 4 % соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?
8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
10. (2017) Имеется два сплава. Первый содержит 5 % никеля, второй — 20 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
11. (2017) Первый сплав содержит 5 % меди, второй — 11 % меди. Масса второго сплава больше массы первого сплава на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
12. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
13. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
Ответы. 7. 400 г. 8. 16 %. 9. 4,8 %. 10. На 75 кг. 11. 6 кг. 12. 5 : 2. 13. 5 : 2.
Для работы с задачами в классе можно использовать вариант заметки в виде презентации: Сплавы и смеси. Задачи 11 из ЕГЭ.
Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение.
М – масса сплава, m – масса меди в сплаве.
|
Было |
M1 |
х кг |
|
m1 |
0,1х кг |
|
|
Добавили |
M2 |
х + 3 |
|
m2 |
(х + 3)0,4 = 0,4х + 1,2 кг |
|
|
Получили |
M3 |
х + х + 3 = 2х + 3 кг |
|
m3 |
(2х + 3)0,3 = 0,6х + 0,9 кг |
Составим уравнение по формуле m3 = m1 + m2.
0,6х + 0,9 = 0,1х + 0,4х +1,2
x = 3.
М3 = 2 . 3 + 3 = 9
Ответ. 9 кг.
Так как третий сплав получен из первого и второго, то его масса равна сумме масс исходных сплавов.
Масса первого сплава известна и равна (displaystyle 3) кг. Поэтому для ответа на вопрос задачи достаточно найти массу второго сплава.
Пусть (displaystyle x) кг – масса второго сплава.
Определим массу меди в третьем сплаве двумя способами:
- с одной стороны, это (displaystyle 30% ) от массы третьего сплава;
- с другой стороны, это сумма масс меди из первого и второго сплавов.
Заметим, что масса меди в третьем сплаве не зависит от способа расчёта. Потому, приравняв найденные выражения, получим уравнение, из которого и найдем массу второго сплава.
Шаг 1
Найдем количество меди как (displaystyle 30% ) от массы третьего сплава.
Так как третий сплав получен из первого и второго, то масса третьего сплава равна (displaystyle (3+x))кг.
Тогда (displaystyle 30%) от (displaystyle (3+x)) кг составляют:
(displaystyle frac{3+x}{100}cdot 30=0{,}3(3+x))кг.
Шаг 2
Найдём суммарную массу меди из первого и второго сплавов.
- Масса меди в первом сплаве – (displaystyle 10%) от (displaystyle 3)кг:
(displaystyle frac{3}{100}cdot 10=0{,}3)кг.
- Масса меди во втором сплаве – (displaystyle 40%) от (displaystyle x)кг:
(displaystyle frac{x}{100}cdot 40=0{,}4x)кг.
Значит, масса меди в третьем сплаве равна (displaystyle 0{,}3+0{,}4x)кг.
Шаг 3
Приравняем массу меди, вычисленную двумя способами:
(displaystyle 0{,}3(3+x)=0{,}3+0{,}4x{small .})
Решим полученное уравнение (displaystyle 0{,}3(3+x)=0{,}3+0{,}4x{small .}) Получаем:
(displaystyle 0{,}9+0{,}3x=0{,}3+0{,}4x{ small ,})
(displaystyle 0{,}3x-0{,}4x=0{,}3-0{,}9{ small ,})
(displaystyle -0{,}1x=-0{,}6{ small ,})
откуда
(displaystyle x=-0{,}6:(-0{,}1)=6:1{ small ,})
(displaystyle x=6) (кг).
Тогда масса третьего сплава равна (displaystyle 3+x=3+6=9) кг.
Ответ: (displaystyle 9)
