Загрузить PDF
Загрузить PDF
Масса – это количество материи, содержащейся в данном теле. Материя – это все, что можно физически ощутить. В большинстве случаев масса зависит от размеров тела, но это не всегда так – например, размеры воздушного шара могут быть больше размеров определенного тела, но при этом масса шара будет меньше массы этого тела. Эта статья расскажет вам, как найти массу.
-
1
Используйте трехрычажные весы. Любые весы используются для нахождения массы тел. В рассматриваемых весах есть три рычага, на каждом из которых имеется передвижная гиря.[1]
Также каждый рычаг снабжен шкалой, вдоль которой двигается гиря определенной массы.[2]
- На показания трехрычажных весов не влияет сила тяжести, что позволяет произвести точные измерения массы. В таких весах неизвестная масса сравнивается с известной массой.
- Средняя шкала имеет шаг 100 г. Дальняя шкала имеет шаг 10 г. Ближняя шкала измеряет вес в диапазоне 0-10 г.
- При помощи трехрычажных весов можно произвести очень точные измерения массы тела. В случае использования таких весов ошибка измерения составит всего 0,06 г. Принцип работы таких весов похож на принцип работы детской карусели.[3]
-
2
Передвиньте гири в крайнее левое положений. Это нужно сделать тогда, когда чаша весов пустая. В этом случае весы будут показывать 0.
- Если индикатор, расположенный справа, не совпадает с фиксированной меткой, откалибруйте весы, поворачивая калибровочный винт (он находится слева под чашей весов).
- Калибруют весы для того, чтобы масса чаши не влияла на показания весов, то есть когда чаша пустая, весы должны показывать 0 г. Масса чаши называется весом тары.
- Для того чтобы с чашей весы показывали 0 г, покрутите калибровочный винт, расположенный под чашей. Затем положите на чашу предмет (тело), массу которого вы хотите найти (это делается при помощи передвижных гирь).
-
3
Двигайте гири по одной. Для начала передвиньте гирю по средней шкале (с шагом 100 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число сотен граммов. За один раз передвигайте гирю на одно деление.
- Затем передвиньте гирю по дальней шкале (с шагом 10 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число десятков граммов.
- Ближняя шкала делений не имеет. Вы можете перемещать гирю по ней в любом направлении. Числа на этой шкале обозначают граммы, а штриховые метки между числами – десятые грамма.
-
4
Найдите массу тела. Теперь вы можете определить массу тела, находящегося на чаше весов. Для этого сложите показания трех шкал.
- Показания каждой шкалы читаются аналогично показаниям линейки. При этом учитывают показания до ближайшей середины между делениями.
- Например, измерим массу банки с содовой. Если дальняя шкала показывает 70 г, средняя шкала показывает 300 г, а ближняя шкала показывает 3,34 г, то масса банки равна 373,34 г.
Реклама
-
1
Вычисление массы через объем и плотность. Формула для вычисления плотности: плотность = масса / объем. Для того чтобы воспользоваться этой формулой, вам нужно знать объем и плотность тела.[4]
- Согласно этой формуле масса тела равна произведению плотности на объем: масса = объем Х плотность. Например, объем алмаза равен 0,00500 кубическим метрам, а его плотность равна 3,520 кгм^3. Для вычисления массы алмаза перемножьте эти значения: 0,00500 Х 3,520.
- Для перемножения значений воспользуйтесь онлайн-калькулятором. Его можно найти на разных сайтах.[5]
[6]
- Вы можете воспользоваться специальным калькулятором для вычисления объема тела. Например, вы можете найти объем конуса, если вам известны радиус его основания и высота.[7]
-
2
Уясните разницу между массой и весом. Это разные величины. Масса – это количество материи, содержащейся в данном теле. Вес – это сила, с которой тело действует на опору и которая возникает в поле силы тяжести. Вес тела возрастает с увеличением его массы.
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
Не забудьте вычислить массу тела в соответствующих единицах измерения (килограммах и граммах), а для обозначения массы используйте специальный символ (букву латинского алфавита). - Вес тел одинаковой массы может быть различным (в зависимости от силы тяжести). Например вес тела на Земле будет отличаться от веса того же тела на Луне.[9]
- Не измеряйте массу тела в фунтах и унциях.[10]
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
-
3
Вычисление массы через силу и ускорение. Формула для вычисление силы: F = m Х a.
- Таким образом, формула для вычисления массы: m = F/a, то есть масса равна силе, деленной на ускорение. Масса тела присутствует в формулировке второго закона Ньютона, который гласит, что ускорение прямо пропорционально вызывающей его силе и обратно пропорционально массе тела.
- Масса измеряется в килограммах (кг). Сила измеряется в ньютонах (Н).[11]
Реклама
Советы
- Масса обозначается буквой m. Масса считается постоянной величиной.
Реклама
Об этой статье
Эту страницу просматривали 19 781 раз.
Была ли эта статья полезной?
Масса, фундаментальное свойство каждого объекта, измеряет количество вещества, содержащегося в теле. В этом посте будет обсуждаться, как найти массу с помощью ускорения и силы, так как это важно при различных подходах и решаемых задачах.
Сэр Исаак Ньютон предложил ряд принципов и теорий, которые привели к разработке нескольких методов оценки массы объекта. Второй закон Ньютона – самый простой и наиболее широко используемый метод расчета массы, поскольку он включает расчет массы с использованием как силы, так и ускорения.
Давайте посмотрим, как второй закон Ньютона может помочь нам в определении массы любого объекта.
Как найти массу с ускорением и силой, используя Второй закон Ньютона:
Термины масса, сила и ускорение используются в повседневной жизни и связаны друг с другом. Сила — это физическое воздействие, вызывающее состояние движения изменяться, что означает, что оно либо ускоряется, либо замедляется. Масса – это тип сопротивления, который предотвращает изменение состояния объекта под действием силы. В результате объект сможет изменить свое состояние движения, как только сила преодолеет это сопротивление.
Наиболее общая форма Второго закона Ньютона гласит, что сила, действующая на тело или частицу, будет равна скорости изменения импульса тела или частицы. Таким образом, поместив это утверждение в формулу, его можно выразить как:
Где p – линейный импульс объекта. Он рассчитывается как произведение скорости и массы объекта. Таким образом, математически мы можем записать это как:
р = мв
Итак, если значение импульс заменяется силой уравнение, получаем:
Когда скорость объекта приближается к скорости света, масса объекта увеличивается; Тем не менее, это не так. Поскольку скорость оцениваемого объекта не очень велика, т.е. близка к скорости света, масса не изменяется. В результате со временем меняется только скорость, а масса остается постоянной.
Но дифференциация скорости во времени дает ускорение.
В результате сила может быть выражена через массу и ускорение, а ее математическое представление выглядит следующим образом:
F = ма
Второй закон Ньютона представлен этим уравнением. Это можно использовать для расчета массы объекта, задав его уравнение. В результате массу объекта можно рассчитать следующим образом:
Ньютон, килограмм и м / с2 – единицы силы, массы и ускорения в системе СИ, соответственно, согласно Международной системе единиц.
Приведенное выше уравнение масс раскрывает два факта, которые перечислены ниже:
- м ∝ F: – Эта пропорциональность показывает, что большая масса требует большей силы, тогда как меньшая масса требует меньшей силы.
- м ∝ 1 / год: – Поскольку ускорение обратно пропорционально массе объекта, объект с большой массой будет испытывать меньшее ускорение, тогда как объект с низкой массой будет испытывать большее ускорение.
Из этого можно сделать вывод, что если масса объекта велика, для него потребуется большая внешняя сила, а поскольку масса, по сути, является сопротивлением, его ускорение будет законом, и наоборот.
Предположим, вы прилагаете силу и к игрушке, и к настоящей машине. Затем игрушечный автомобиль разгоняется без особых усилий. Однако настоящей машине для движения вперед требуется больше силы. Или, возможно, он вообще не двигается. Это связано с тем, что масса игрушечной машинки меньше, чем у реальной машины. В результате сила, необходимая для их ускорения, варьируется.
Давайте посмотрим на некоторые проблемы нахождения массы с помощью ускорения и силы.
Проблема: когда к объекту прилагается сила в 6.0 ньютонов, он ускоряется со скоростью 12.0 м / с2. Определите массу объекта.
Данный:
Сила на объект F = 6 Н
Ускорение объекта a = 12 м / с2
Найти:
m =?
Решение:
Масса объекта:
∴ м = 2 кг
Таким образом, здесь, в данном случае, масса объекта составляет 2 кг.
Проблема: чтобы разогнать мяч со скоростью 4 м / с2, требуется сила 24 Н. Какой тогда была бы масса объекта?
Данный:
Ускорение мяча a = 4 м / с2
Сила, приложенная к шару F = 24 Н
Найти:
m =?
Решение:
Масса мяча:
∴ м = 6 кг
Таким образом, чтобы разогнаться со скоростью 4 м / с2, мячу весом 6 кг требуется сила 24 Н.
Часто задаваемые вопросы о поиске массы с помощью второго закона Ньютона:
В .: Приведите законы движения Ньютона.
Ответ: Формулировки всех трех законов движения Ньютона приведены ниже:
1-й закон: Состояние тела не изменяется до тех пор, пока на него не перестанет действовать ненулевая результирующая сила, что означает, что если оно неподвижно, оно останется таковым, а если оно движется, оно будет поддерживать свою скорость. Это часто называют законом инерции.
2-й закон: Скорость изменения импульса тела пропорциональна приложенной к нему силе. Или, другими словами, величина ускорения объекта пропорциональна приложенной к нему силе и обратно пропорциональна массе тела. Это можно записать в виде уравнения:
F = ma
3-й закон: Во время взаимодействия двух тел сила, действующая обоими, будет одинаковой по величине и в противоположном направлении.
В: Когда ракета запускается со стартовой площадки, она не только набирает скорость, но и получает огромное ускорение во время стрельбы. Что является причиной этого?
Отв.: Когда ракета запускается, она ускоряется в результате выстрела.
Из-за топлива, используемого в ракетах, стрельба из них возможна. Топливо в ракете горит во время выстрела. В результате постоянной стрельбы масса теряется, а ускорение увеличивается, потому что масса и ускорение обратно пропорциональны.
В: Объясните, как каждый из законов Ньютона влияет на игру в перетягивание каната.
Отв .: Важность каждого закона Ньютона в перетягивании каната указана ниже:
- Первый закон Ньютона: Пока не начнется тяга, то есть пока не будет приложена сила, веревка останется в том же положении.
- Второй закон Ньютона: Силу каждой команды можно рассчитать с помощью второго закона Ньютона. Сила, с которой тянет каждая команда, определяется массой тела каждой команды и ускорением, с которым движется веревка.
- Третий закон Ньютона: Одна команда с силой тянет веревку к себе, а другая тянет веревку от себя. Обе команды, по сути, идут в противоположных направлениях. В результате, пока одна из сторон не достигнет максимума, ни одна из команд не выиграет.
В. Опишите, что произойдет, если вы попытаетесь толкнуть кого-то, кто тяжелее вас. Что, если он тоже оттолкнет вас?
Ответ: Тело будет ускоряться только в том случае, если действующая на него результирующая сила больше нуля.
Поскольку человек, которого вы пытаетесь толкнуть, имеет большую массу, чем вы, ему потребуется больше силы для ускорения, чем вы можете предоставить. В результате человек останется неподвижным. Поскольку ваша масса меньше его, когда он толкает вас назад, вы ускоряетесь в направлении толчка.
Мы видели, как найти массу без ускорения в предыдущем посте, а в этом – как найти массу с ускорением и силой. Мы надеемся, что эти сообщения ответили на ваши вопросы.
Содержание:
- Определение и формула массы тела
- Инертная масса
- Гравитационная масса
- Формула расчета массы через плотность тела
- Масса в специальной теории относительности
- Примеры решения задач
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (mi):
$$m=sum_{i=1}^{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$bar{F}=m bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (Ft) избранного тела:
$$m=frac{F_{t}}{g}(3)$$
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
$$m=int_{V} rho d V(4)$$
где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:
$m = rho V (5)$
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Примеры решения задач
Пример
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
$$E^{prime}=M c^{2}(1.1)$$
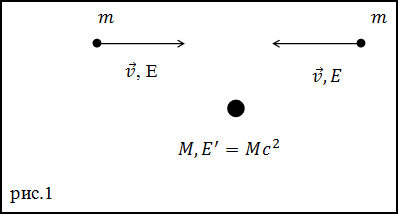
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Масса является одним из важных свойств материи. Это понятие применяют при решении задач различного характера, начиная от проблем в механике и заканчивая химическими расчетами. Рассмотрим в статье, с помощью каких формул массу в физике можно рассчитать.
Что это такое?
Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.
 Вам будет интересно:Слово “кворум”. Значение и происхождение термина. Нюансы определения
Вам будет интересно:Слово “кворум”. Значение и происхождение термина. Нюансы определения
Масса бывает двух важных видов:
- инерционная;
- гравитационная.
Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.
Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.
Формулы для инерции
В физике формула нахождения массы инерционной имеет следующий вид:
m = F / a
Здесь F – сила, которая на тело действует и вызывает появление у него ускорения a. Формула показывает, что чем больше будет действующая сила и чем меньше она сообщит ускорение телу, тем больше инерционная масса m.
Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:
m = p / v
Здесь p – количество движения (импульс), v – скорость тела. Чем большим количеством движения обладает тело и чем меньше его скорость, тем большую инерционную массу оно имеет.
Формула для гравитации
Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:
F = G * m1 * m2 / r2
Где r – расстояние между телами, G – некоторая постоянная.
Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:
m = F / g
Здесь F – сила тяжести, g – ускорение, с которым тела падают на землю вблизи ее поверхности.
Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес – величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.
Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Плотность и объем
Как было отмечено, масса – это неотъемлемое свойство материи, поэтому ее можно вычислить с помощью других физических характеристик тел. Этими характеристиками являются объем и плотность.
Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.
Плотность – это свойство вещества, которое отражает количество материи, помещенной в единице объема.
Формула массы вещества через объем и плотность записывается так:
m = ρ * V
Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.
Относительная
Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).

Формулу относительной массы M можно записать так:
M = ma / (1 / 12 * mC)
Где ma – масса атома в килограммах, mC – масса атома углерода в килограммах. Например, если в это выражение подставить значение массы атома кислорода, то его а. е. м. будет равна:
M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.
Поскольку а. е. м. является относительной величиной, то она не имеет размерности.
Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.
Энергия

Выше были приведены разные формулы, как найти массу в физике. Завершая статью, хотелось бы отметить связь массы и энергии. Это связь носит фундаментальный характер, который отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула массы в физике, полученная Альбертом Эйнштейном, имеет вид:
E = m * c2
Квадрат скорости света c является коэффициентом перевода между массой и энергией. Это выражение говорит о том, что обе величины, по сути, являются одной и той же характеристикой материи.
Записанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.
