Задачи на Закон сохранения импульса с решениями
Формулы, используемые на уроках «Задачи на импульс тела. Задачи на Закон сохранения импульса».
Название величины |
Обозначение |
Единица измерения |
Формула |
Скорость тела |
v |
м/с |
v = p/m |
Масса тела |
m |
кг |
m = p/v |
Импульс тела (модуль) |
p |
кг•м/с |
p = m•v |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определите массу автомобиля, имеющего импульс 2,5•104 кг•м/с и движущегося со скоростью 90 км/ч.
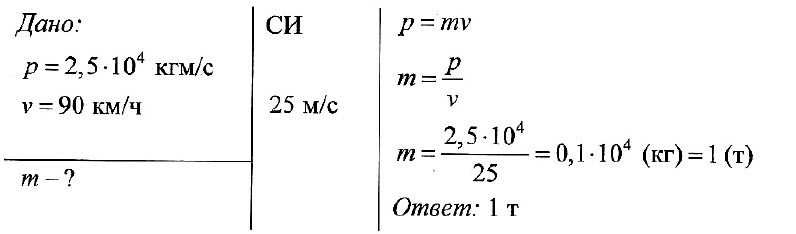
Задача № 2.
Тележка массой 40 кг движется со скоростью 4 м/с навстречу тележке массой 60 кг, движущейся со скоростью 2 м/с. После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки ?
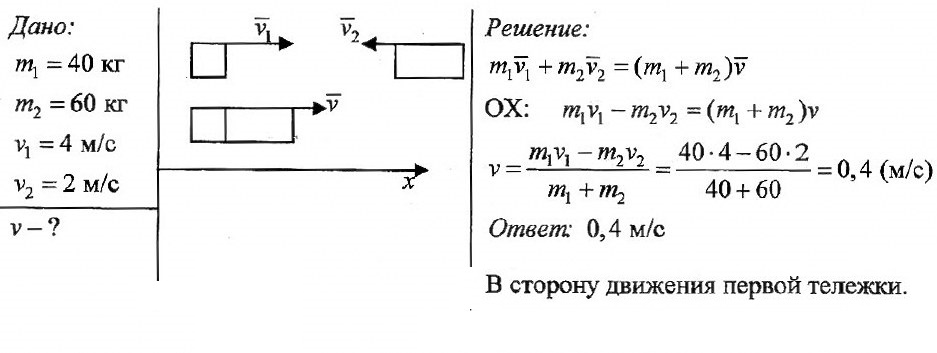
Задача № 3.
Снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории. Первый осколок массой 1 кг приобрел скорость 400 м/с, направленную горизонтально. Второй осколок массой 1,5 кг полетел вверх со скоростью 200 м/с. Какова скорость третьего осколка, если его масса равна 2 кг?
Решение. Взрывающийся снаряд можно считать замкнутой системой, потому, что сила тяжести намного меньше, чем сила давления пороховых газов, разрывающих снаряд на осколки. Значит, можно использовать закон сохранения импульса. Поскольку разрыв снаряда произошел в верхней точке траектории, векторная сумма импульсов всех осколков должна быть равна нулю. Следовательно, векторы импульсов осколков образуют треугольник; этот треугольник прямоугольный, а искомый вектор — его гипотенуза.

Ответ: 250 м/с.
Задача № 4.
К стене прикреплен шланг с насадкой, изогнутой под прямым углом (см. рисунок). Из шланга вытекает вода со скоростью v = 10 м/с. Найдите горизонтальную составляющую силы, с которой шланг давит на стену. Площадь сечения шланга S = 10 см2.

F = 1000 (кг/м3) • 0,001 (м2) • 100 (м2/с2) = 100 (кг/м•с2)
Ответ: 100 Н.
Задача № 5.
Какую силу тяги развивает реактивный двигатель, выбрасывающий каждую секунду 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты?

Ответ: 30 кН.
Задача № 6. Повышенной сложности
Конькобежец массой М = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью v = 8 м/с относительно льда. Найдите, на какое расстояние S откатится при этом конькобежец, если μ = 0,02.

Ответ: 0,3 м.
Задача № 7. Повышенной сложности
Деревянный брусок, движущейся вертикально, падает со скоростью v = 3 м/с на горизонтальную ленту транспортера, движущегося со скоростью u = 1 м/с. Брусок после удара не подскакивает. При каком коэффициенте трения брусок не будет проскальзывать по транспортеру?
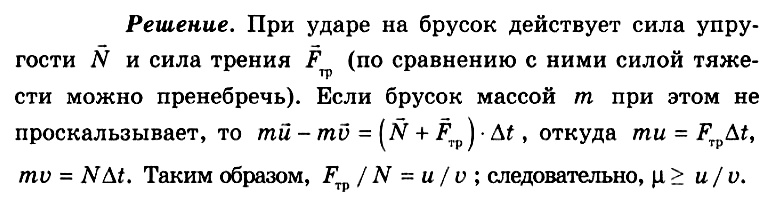
Ответ: μ ≥ 0.33
Задача № 8.
ОГЭ
Конькобежец массой M = 70 кг, стоя на льду, бросает в горизонтальном направлении шайбу массой m = 0,3 кг со скоростью v = 40 м/с. На какое расстояние s откатится конькобежец, если коэффициент трения коньков о лёд μ = 0,02?

Задача № 9.
ЕГЭ
Вагон массой m = 4•104 кг, движущийся со скоростью v = 2 м/с, в конце запасного пути ударяется о пружинный амортизатор. На сколько он сожмёт пружину амортизатора, жёсткость которой k = 2,25•106 Н/м?

Краткая теория для решения задачи на Закон сохранения импульса.

Алгоритм решения задач на закон сохранения импульса:
1. Записать «дано».
2. Сделать чертеж, на котором изобразить направления импульсов (или скоростей) каждого тела до взаимодействия и после взаимодействия.
3. Записать закон сохранения импульса для данной системы в векторной форме.
4. Выбрать координатную ось (оси), найти проекции векторов на эту ось (оси).
5. Записать закон сохранения импульса в скалярной форме.
6. Решить получившееся уравнение относительно неизвестной величины.
7. Оценить ответ на реальность.
Рассмотрим взаимодействия тел, при котором они движутся вдоль одной прямой в одном направлении или навстречу друг другу. При столкновении тела испытывают соударение. Соударение может быть двух типов: упругий удар и неупругий удар.
Упругий удар — тела после взаимодействия приобретают скорости, направленные в разные стороны.
Неупругий удар — тела после взаимодействия будут двигаться вместе, как одно целое.
Это конспект по теме «ЗАДАЧИ на Закон сохранения импульса». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Механические колебания
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Сегодня в рубрике «Физика для чайников» занимаемся решением и разбором задач на закон сохранения импульса. И не говорите, что вы этого не ждали.
Полезные лайфхаки и новости для студентов – ежедневно на нашем телеграм-канале. Подписывайтесь!
Задачи на закон сохранения импульса с решением
Задача №1 на нахождение импульса
Условие
Небольшой автомобиль движется со скоростью 60 км/ч, его импульс равен 1,5*10^4 кг*м/с. Какова масса автомобиля?
Решение
По формуле для импульса найдем:
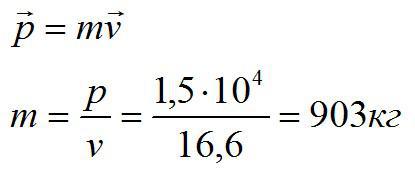
Ответ: 903 кг.
Задача №2 на закон сохранения импульса
Условие
Дрезина массой 400 кг движется со скоростью 4 м/с, а навстречу ей со скоростью 2 м/с едет дрезина массой 60 кг. После неупругого соударения дрезины движутся вместе. В каком направлении и с какой скоростью будут двигаться дрезины?
Решение
Общий импульс системы до и после соударения должен остаться неизменным:
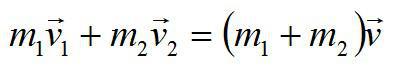
Запишем закон сохранения импульса в проекции на горизонтальную ось:
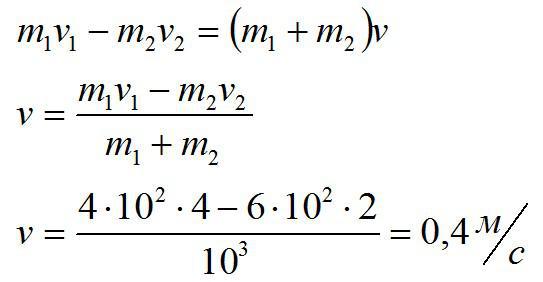
Движение будет происходить в сторону первой дрезины. Именно она изначальна имела больший импульс.
Ответ: 0,4 м/с.
Задача №3 на нахождение импульса
Условие
Тело массой m=1 кг упало с высоты H=19,6 м. Определить изменение импульса тела за последнюю секунду движения и импульс тела на высоте h=4,9 м.
Решение
Изменение импульса тела за последнюю секунду движения равно:
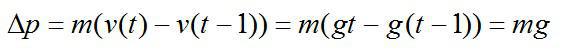
Импульс тела на заданной высоте найдем по закону сохранения энергии, который имеет вид для двух состояний:
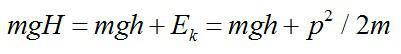
Отсюда получим:
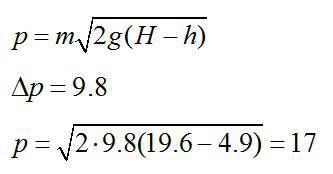
Ответ: Изменение импульса равно 9,8 кг*мс2; р=17 кг*мс2.
Задача №4 на применение закона сохранения импульса и второго закона Ньютона
Условие
Хоккеист массой М = 70 кг стоит на льду и бросает в горизонтальном направлении шайбу массой m = 3 кг со скоростью v = 8 м/с относительно льда. На какое расстояние S откатится при этом конькобежец, если коэффициент трения равен 0,02.
Решение
По закону сохранения импульса найдем скорость u, с которой хоккеист откатиться назад:
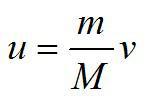
По второму закону Ньютона для хоккеиста:
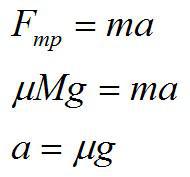
С другой стороны:
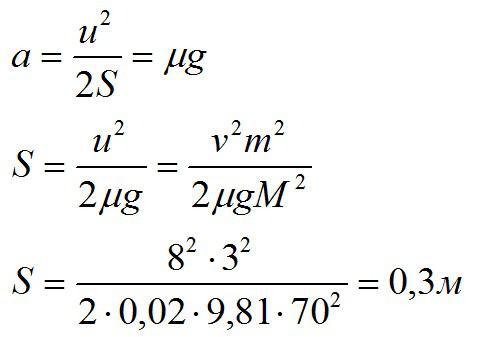
Ответ: 0,3 м.
Задача №5 на реактивное движение
Условие
Реактивный двигатель каждую секунду выбрасывает 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты. Какую силу тяги он развивает?
Решение
Запишем второй закон Ньютона в импульсной форме и найдем силу, которая действует на выбрасываемые продукты сгорания топлива:
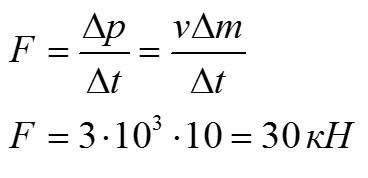
По третьему закону Ньютона сила тяги будет равна найденной силе.
Ответ: 30 кН.
Вопросы на закон сохранения импульса
Вопрос 1. Что такое замкнутая система?
Ответ. Замкнутая система – такая система, на которую не действуют внешние силы со стороны других тел.
Вопрос 2. Что такое импульс силы?
Ответ. Импульс силы – физическая величина, равная произведению силы на время ее действия.
Вопрос 3. Как направлен импульс тела?
Ответ. Направление импульса совпадает с направлением вектора скорости тела.
Вопрос 4. Что такое реактивное движение?
Ответ. Реактивное движение – движение, основанное на принципе отдачи. По аналогии с системой «пушка-ядро», систему «ракета-выхлопные газы» также можно считать замкнутой.
Вопрос 5. Два тела разной массы движутся с одинаковой скоростью. Импульс какого тела больше?
Ответ. Тело с большей массой обладает большим импульсом.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Импульс и закон сохранения импульса
Что такое импульс в механике
Импульс, или количество движения – векторная физическая величина, равная произведению массы тела на его скорость.
Обозначается латинской буквой p и измеряется в килограммах на метр в секунду.
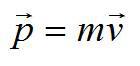
Второй закон Ньютона с применением импульса можно записать следующим образом:
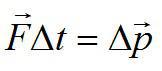
Здесь дельта p – изменение импульса тела за время дельта t под действием равнодействующей силы F.
Закон сохранения импульса
Этот фундаментальный закон природы и гласит:
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Закон сохранения импульса является следствием второго и третьего законов Ньютона.
Более подробную теорию по этой и другим темам вы найдете в нашем справочнике.
Пример действия закона сохранения импульса
Представим себе пушку, которая стреляет ядрами. Систему «пушка-ядро» можно считать замкнутой. При стрельбе из пушки действует закон сохранения импульса. Ядро летит в одну сторону, а пушка под действием отдачи откатывается назад. При этом скорость, приобретенная пушкой, зависит от соотношения масс орудие/ядро и скорости ядра.
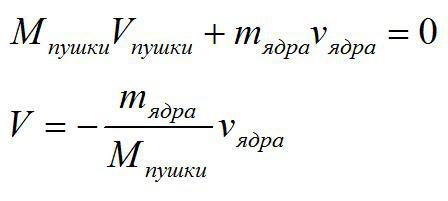
Знак минус указывает на то, что пушка и ядро движутся в разные стороны.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис.
Импульс .
( P=mv )
( p ) -импульс
( m ) -масса
(v ) – скорость
Изменение импульса .
( Delta P=Ft )
( Delta P ) – Изменение импульса
( F ) – Сила
(t ) – Время
1. Вычислить импульс тела массой (m=6 кг ),движущегося со
скоростью (v=4 м/с ) .
Показать ответ
Показать решение
Видеорешение
2. Вычислить импульс самолета массой (m=600 кг ), движущегося со
скоростью (v=50 м/с ) .
Показать ответ
Показать решение
Видеорешение
3. Вычислить скорость самолета массой (m=500 кг ), если его импульс
(P= 35000 кг cdot м/с ).
Показать ответ
Показать решение
Видеорешение
4. Вычислить массу вертолета, летящего со скоростью (v=30 м/с ), если его импульс
(P= 18000 кг cdot м/с ).
Показать ответ
Показать решение
Видеорешение
5. Вычислить скорость автобуса массой (m=8000 кг ), если его импульс
(P= 72000 кг cdot м/с ).
Показать ответ
Показать решение
Видеорешение
6. Грузовой автомобиль едет со скоростью (v=54 км/ч ) ,
его импульс (P= 45000 кг cdot м/с ).
Найти массу грузового автомобиля.Ответ дать в системе СИ.
Показать ответ
Показать решение
Видеорешение
7. Снегоход едет со скоростью (v=18 км/ч ) ,
его импульс (P= 1500 кг cdot м/с ).
Найти массу снегохода .Ответ дать в системе СИ.
Показать ответ
Показать решение
Видеорешение
8. Вычислить скорость автобуса массой (m_1=8000 кг ), если его импульс
равен импульсу легкового автомобиля массой (m_2=1000 кг ), движущегося со скоростью (v_2=40 м/с ) .
Показать ответ
Показать решение
Видеорешение
9. Вычислить скорость мотоцикла массой (m_1=200 кг ), если его импульс
равен импульсу парусной яхты массой (m_2=1000 кг ), движущейся со скоростью (v_2=6 м/с ) .
Показать ответ
Показать решение
Видеорешение
10. Импульс пули , выпущенной из пистолета со скоростью (v_п=400 м/с ) равен импульсу стрелы выпущенной
из арбалета со скоростью (v_с=90 м/с ) .
Масса пули (m_п=0,009 кг). Вычислить массу стрелы.Ответ дать в граммах.
Показать ответ
Показать решение
Видеорешение
11. Импульс бензовоза массой (m_1=12 т ) , движущегося со скоростью (v_1=50,4 км/ч ) равен импульсу
самолета массой (m_2=2 т ) .
Вычислить скорость самолета.Ответ дать в системе СИ.
Показать ответ
Показать решение
Видеорешение
13. Найти изменение импульса грузового автомобиля массой (m=5,5 т )
при увеличении его скорости с (v_1=54 км/ч ) до (v_2=90 км/ч ).
Ответ дать в системе СИ.
Показать ответ
Показать решение
Видеорешение
14. Найти изменение импульса троллейбуса массой (m=15,5 т )
при увеличении его скорости с (v_1=7,2 км/ч ) до (v_2=25,2 км/ч ).
Ответ дать в системе СИ.
Показать ответ
Показать решение
Видеорешение
17. На тело, покоящееся на гладкой горизонтальной поверхности,
начинает действовать сила (F=5 Н ) в течении (t=4 с ) .
Найти изменение импульса этого тела после окончания действия силы.
Показать ответ
Показать решение
Видеорешение
18. На тело покоящееся на гладкой горизонтальной поверхности
начинает действовать сила (F=5 Н ) в течении (t=4 с ) .
Какой импульс приобретет это тело после окончания действия силы?
Показать ответ
Показать решение
Видеорешение
20. Определить по графику изменение импульса тела в момент времени (t=5 с ) .
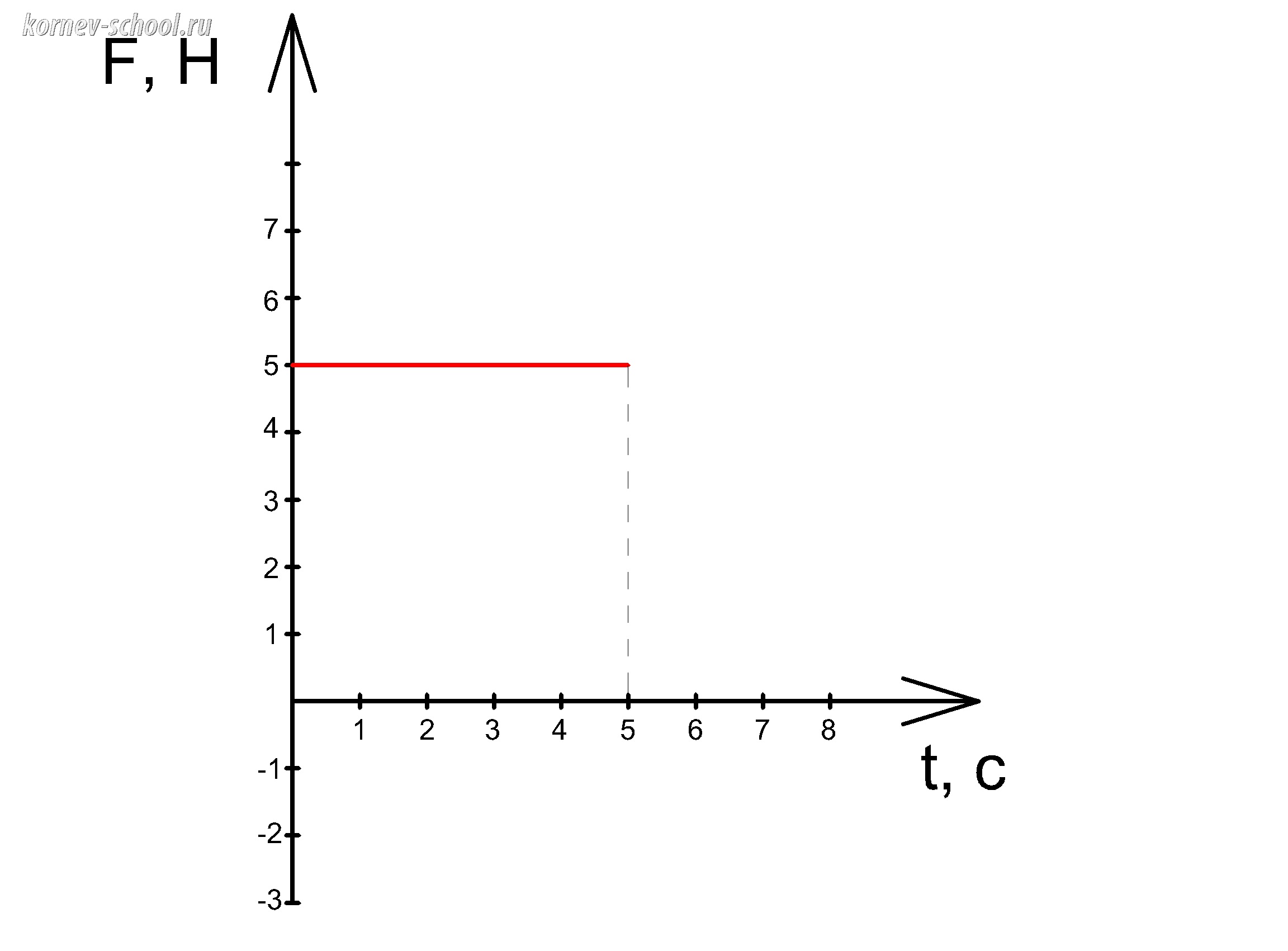
Показать ответ
Показать решение
Видеорешение
Задача 30.
Трамвай движется со скоростью (V_1=5 м/с ; , ) а автомобиль со скоростью (V_2=20 м/с ; , ) Масса трамвая ( m_1=18000 кг ; , )
Отношение величины импульса трамвая к величине импульса автомобиля равно 2,25.
Чему равна масса автомобиля?
Ответ дать в килограммах.
Показать ответ
Показать решение
Видеорешение
- Подробности
- Обновлено 30.05.2018 23:14
- Просмотров: 1422

Задачи по физике – это просто!
Вспомним
Расчетная формула закона сохранения импульса в проекциях векторов для решения задач:

При столкновении двух тел:
упругий удар – после соударения тела движутся с разными скоростями;
неупругий удар – после соударения оба тела движутся, как одно целое (“в сцепке”), в одном направлении и с одинаковой скоростью.
Для успешного решения задачи на закон сохранения импульса удобнее сделать два чертежа ( до и после взаимодействия).
Иногда при решении задачи невозможно заранее определить направление движения какого-либо тела после взаимодействия. Тогда это направление вектора скорости тела выбирается произвольно.
Если в результате решения задачи проекция выбранного вектора окажется положительной, то его направление выбрано правильно, если отрицательна, то истинное направление вектора противоположно. Несмотря на это, в обоих случаях задача решена правильно.
Не забываем
Решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики на закон сохранения импульса.
Задача 1
Шар массой 2 кг движется со скоростью 4 м/с и сталкивается с неподвижным шаром массой 6 кг. Какова будет скорость и направление движения первого шара после упругого удара, если скорость неподвижного шара после удара окажется равной 1 м/с?

Задача 2
2 шара с массами 10 кг и 20 кг движутся по горизонтальному желобу навстречу друг другу со скоростями 4 м/с и 6 м/с соответственно.
Определить модуль скорости и направление движения каждого шара после неупругого столкновения.

Задача 3
C тележки массой 10 кг, которая движется по горизонтальной прямой со скоростью 1 м/с, спрыгивает мальчик массой 40 кг со скоростью 3 м/с в направлении противоположном направлению движения тележки. Определить скорость тележки сразу после прыжка мальчика.

Задача 4
На тележку массой 6 кг, движущуюся со скоростьью 2 м/с, сверху вертикально вниз падает кирпич массой 2 кг. Какова будет скорость тележки сразу после падения кирпича?

Закон сохранения импульса
Закон сохранения импульса
Импульс замкнутой системы, состоящей из (n), тел остается постоянным с течением времени при любых взаимодействиях тел внутри данной системы
[displaystylesum_{i=1}^{n}vec{p}_i=displaystylesum_{i=1}^{n}m_ivec{v}_i=const]
Охотник, стоящий на гладком льду, стреляет из ружья. Масса заряда (0,05 text{кг} ). Скорость снаряда (200 text{м/c}). Какова масса охотника, если его скорость после выстрела равна (0,1 text{м/c})
Так как до выстрела общий импульс системы равен нулю. По Закону Сохранения импульса: [m_1cdot upsilon_1 – m_2cdot upsilon_2 = 0] Где (m_2) – масса охотника, (m_1) – масса снаряда (v_1), (upsilon_2) – скорости снаряда и охотника соответственно [m_2 = frac {m_1 cdot upsilon_1} {upsilon_2}] [m_2= frac {0,05 text {кг} cdot 200 text{ м/с}}{0,1 text{м/c} } =100text{ кг}]
Ответ: 100
Камень массой (m =4 text { кг} ) падает под углом (alpha=30^circ) к вертикали со скоростью (10 text { м/с}) в тележку с песком общей массой ( M= 16 text { кг}), покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в неё камня.
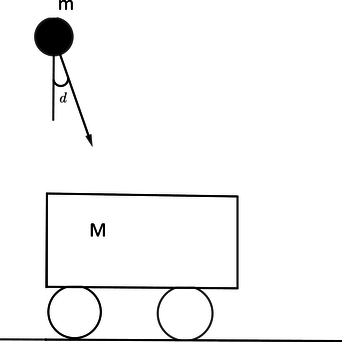
В начале импульс тележки равен нулю. по Закону Сохранения Импульса(на горизонтальную ось): [m_1cdot upsilon_1sinalpha=(m+M)cdotupsilon’] [upsilon’=frac{m_1cdot upsilon_1sinalpha}{m+M}] [upsilon’=frac{4text{ кг}cdot 10text{ м/с} cdotdfrac 1 2 }{4text{ кг}+16text{ кг}}=1text{ м/c}]
Ответ: 1
С неподвижной лодки массой (M=50text{ кг } ) на берег прыгнул мальчик массой (m=40text{ кг } ) со скоростью (upsilon_1 = 1 text{ м/c } ) относительно берега, направленной горизонтально. Какую скорость (upsilon_2) относительно берега приобрела лодка?
Начальный импульс системы равен нулю. По закону Сохранения Импульса: [Mcdotupsilon_2-mcdotupsilon_1 = 0] [upsilon_2=frac{mcdotupsilon_1}{M}] [upsilon_2=frac{40 text{ кг }cdot 1 text{ м/с } } {50 text{ кг}} =0,8 text{ м/c }]
Ответ: 0, 8
Одинаковые шары массой (m = 1 text{ кг } ) каждый движутся со скоростями, направления которых указаны на рисунке, и сталкиваются. Чему будет равен суммарный импульс шаров после столкновения, если (upsilon_1=16 text{ м/c }), а (upsilon_2=upsilon_1 cdot sqrt{2})?
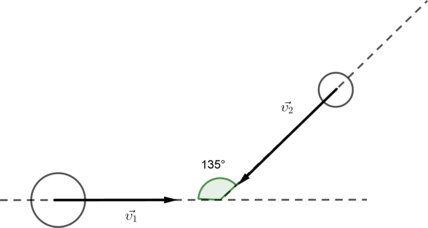
Из рисунка видно, что углы между осями и вторым шаром равны (45^circ). По закону сохранения импульса суммапрный импульс системы до удара и после удара будет одинаковый. Найдем проекции суммарного импульса на каждую ось: (p_x’) – Суммарный импульс на ось Ox (p_y’) – суммарный импульс на ось Oy [p_{2x}-p_{1x}=p_x’] [p_{2y}-p_{1y} =p_y’] По рисунку (p_{1y}=0) По теореме Пифагора: [P_{text{итог}}’=sqrt{p_y’^2+p_x’^2}] Заменим (upsilon_2) на (upsilon_1 cdot sqrt{2} ). [p_y’=mcdotupsilon_1sqrt{2}cos{45^circ}] [p_x’=mcdot upsilon_1cdot (cos{45^circ} cdot sqrt{2}-1)] [p_y’= 1 text{кг} cdot 16 text{ м/c } cdot frac{sqrt2} 2cdot sqrt 2 = 16 frac{text{ кг }cdot text{ м }} {text{ c }}] [p_x’= 1 кг cdot 16 text{м/c} left(frac{sqrt2} {2} cdot sqrt2 – 1right)=0frac{text{ кг }cdot text{ м }} {text{ c }}] [P_{ итог } = sqrt{left(16frac{text{кг}cdot text{м}} { c}right)^2}=16frac{text{ кг }cdot text{ м }} { text{ c } }]
Ответ: 16
На неподвижный бильярдный шар налетел другой такой же. После удара шары разлетелись под углом (90^circ) так, что импульс одного равен (p_1=5dfrac {text{ кг }cdot text{ м }} {text{ c }} ), а другого (p_2 = 12dfrac{text{ кг }cdot text{ м }}{text{ c }}) (см.рисунок). Чему был равен импульс налетающего шара?
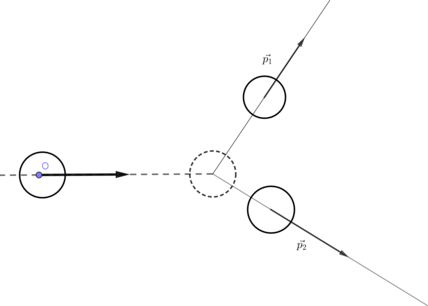
По закону сохранения импульса: [vec{p’}=vec{p_1}+vec{p_2}] Так как шары разлетелись под углом (90^{circ}), применим теорему Пифагора: [p’=sqrt{p_1^2 + p_2^2}] [p’=sqrt{left(5 frac {text{ кг }cdot text{ м }} {text{ c }} right)^2 + left(12frac {text{ кг }cdot text{ м }} {text{ c }} right)^2}=13frac {text{ кг }cdot text{ м }} {text{ c }}]
Ответ: 13
По гладкой горизонтальной плоскости по осям Оx и Оy движутся две шайбы с импульсами равными по модулю (p_1 =3 ) кг(cdot)м/с и (p_2 =6 ) кг(cdot)м/с (см.рисунок). После их соударения вторая шайба продолжает двигаться по оси y в прежнем направлении. Модуль импульса первой шайбы после удара равен (p_1’= 5 ) кг(cdot)м/с. Найдите модуль импульса второй шайбы после удара.
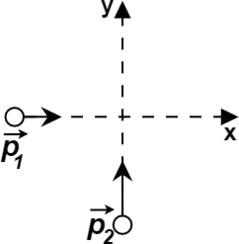
Запишем ЗСИ (закон сохранения импульса): [vec{p_1}+vec{p_2}=vec{p_1}’+vec{p_2}’ quad(1)] Спроецируем данное уравнение на ось Оx: [p_1=p_{1x}’ quad(2)] Спроецируем на ось Оy: [p_2=p_{1y}’+p_2′ quad(3)] После удара импульс первой шайбы стал равен [p_1’=sqrt{p_{1x}^{prime 2}+p_{1y}^{prime 2}} quad(4)] Из (2) следует, что (p_{1x}’ =3 ) кг(cdot)м/с. Из (4) следует, что [p_{1y}=sqrt{p_1^{prime 2}- p_{1x} ^{prime 2}}=sqrt{25-9} = 4 text{ кг$cdot$м/c}]
Найдем (p_2′) из (3): [p_2’=p_2-p_{1y}’= 6 – 4 = 2text{ кг·м/c}]
Ответ: 2
Снаряд, выпущенный вертикально вверх, мгновенно разрывается в высшей точке траектории на два осколка, массы которых (m) и (4m). Скорость лѐгкого осколка сразу после взрыва (upsilon_1=500) м/с. Найдите скорость (upsilon_2) второго осколка сразу после взрыва.
Суммарный импульс снаряда до взрыва равен 0 (так как взрыв происходит в наивысшей точки траектории), следовательно сразу после взрыва суммарный импульс тоже равен 0: [0=vec{p_1}+vec{p_2}] где (p_1) и (p_2) – это импульс первого и второго осколка. Найдем скорость второго осколка: [mupsilon_1=4mupsilon_2] [upsilon_2=frac{upsilon_1}{4}=frac{500}{4}=125 text{ м/с}]
Ответ: 125
