Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
– масса раствора = масса воды + масса соли;
– масса сплава равна сумме масс металлов, входящих в этот сплав;
– масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе – это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс – масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси – это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв – масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве – это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв – масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М – масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% – 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
Наибольшие трудности при изучении физики
учащиеся испытывают при решении задач, т.е. когда
требуется применить знания. Эти трудности
представляются ребятам настолько большими, что
многие из них отказываются даже от попыток
решать задачи. Отказ от решения задач еще как-то
«проходил» во времена устных экзаменов по
физике. Но теперь – как при прохождении
Государственной итоговой аттестации, выполнении
заданий Единого государственного экзамена или
тестирования при поступлении – проверяют именно
умение применять полученные знания, а не
декларировать их.
Понимание смысла физических законов – главная
цель школьного курса физики, но понимание этих
законов может родиться только в осознанной
деятельности по применению этих законов.
Школьникам же часто предлагают алгоритмы
решения задач, которые провоцируют бездумное,
автоматическое применение физических формул.
Преодолеть эту принципиальную трудность можно,
только неоднократно применяя законы физики в
тщательно отобранных простейших ситуациях,
когда смысл этих законов кристально ясен.
В школьном курсе физики тысячи задач. Однако,
если посмотреть на все множество этих задач «с
высоты птичьего полета», то нетрудно заметить,
что подавляющее их большинство группируются
вокруг нескольких десятков типичных учебных
ситуаций. Эти ситуации можно назвать ключевыми.
А овладение ключевыми ситуациями «даст ключи» к
решению задач.
Ключевые ситуации – важнейшая связь между
«теорией» и «задачами». Без этой связи теория
мертва для школьника, а задачи представляются
ему случайной россыпью неинтересных загадок.
Однако пока еще некоторые учителя «дают» своим
ученикам «теорию» отдельно, а «задачи» отдельно.
После такого разрезания по живому от живой
физики остаются только мертвые формулы-шаблоны
для примитивных задач на подстановку.
Изучение ключевых ситуаций – это живой мост
между «теорией» и «задачами», причем мост с
двухсторонним движением. С одной стороны, задачи
рождаются при изучении ключевых ситуаций, в
которых наглядно проявляется действие
физических законов, с другой стороны, благодаря
решению задач на основе ключевой ситуации теория
осознается, т.е. становится действенной силой, а
не пассивным набором фактов и формул.
И еще одна очень важная роль ключевых ситуаций.
Дело в том, что результатом изучения школьного
курса физики должен быть не набор решенных задач
(это быстро забывается), а понимание физических
законов и физическая интуиция, которая может
развиваться именно при рассмотрении ключевых
ситуаций.
Приложение 1.
Фрагмент урока с выделением ключевой ситуации по
теме «Плотность».
Приложение 2. Фрагмент
урока с выделением ключевой ситуации по теме
«Полые тела».
Приложение 3.
Дополнительный материал по теме «Сплавы».
Приведем фрагмент урока с выделение ключевой
ситуации по теме «Сплавы».
Фрагмент урока по теме «СПЛАВЫ»
Учитель. Тема урока зашифрована
ребусом. Кто первый раскроет секрет?

Ученики. …
Учитель. Тема урока «Сплавы».
Сплав — макроскопически однородная смесь двух
или большего числа химических элементов с
преобладанием металлических компонентов.
Основной или единственной фазой сплава, как
правило, является твёрдый раствор легирующих
элементов в металле, являющемся основой сплава.
Сплавы имеют металлические свойства, например:
металлический блеск, высокие электропроводность
и теплопроводность. Иногда компонентами сплава
могут быть не только химические элементы, но и
химические соединения, обладающие
металлическими свойствами. Например, основными
компонентами твёрдых сплавов являются карбиды
вольфрама или титана. Макроскопические свойства
сплавов всегда отличаются от свойств их
компонентов, а макроскопическая однородность
многофазных (гетерогенных) сплавов достигается
за счёт равномерного распределения примесных
фаз в металлической матрице.
Сплавы обычно получают с помощью смешивания
компонентов в расплавленном состоянии с
последующим охлаждением. При высоких
температурах плавления компонентов, сплавы
производятся смешиванием порошков металлов с
последующим спеканием (так получаются, например,
многие вольфрамовые сплавы).
Сплавы являются одним из основных
конструкционных материалов. Среди них
наибольшее значение имеют сплавы на основе
железа и алюминия. В состав многих сплавов могут
вводиться и неметаллы, такие как углерод,
кремний, бор и др. В технике применяется более 5
тыс. сплавов.
Цель нашего урока –
научиться решать задачи для определения
плотности, массы или объема сплавов или веществ
входящих в их состав.
Рассматривая сплавы, обычно предполагают, что
объем сплава равен сумме объемов
составляющих его веществ. В таком случае
плотность сплава ![]() ,
,
где индексы 1 и 2 относятся к двум компонентам
сплава.
Если заданы или требуется найти массы
компонентов известной плотности ρ1 и ρ2, то объемы
компонентов надо выразить через их массы и
плотности, в результате чего формула для
плотности сплава примет вид 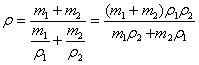 .
.
Часто в задаче дано или требуется найти
соотношение масс компонентов сплава. Обозначим ![]() . Тогда
. Тогда ![]() . Эта формула связывает
. Эта формула связывает
плотность сплава ρ и массовое отношение
компонент ![]() . Из
. Из
нее при ![]() следует:
следует:
![]() . Приведенные
. Приведенные
формулы позволяют по заданному значению одной из
величин (![]() или ρ)
или ρ)
найти значение другой.
Запишите в тетрадях:
Примечание.
1. Задача первого уровня предназначена для
применения основной формулы: ![]() .
.
2. Задачи второго уровня похожи, поэтому
целесообразно применить разные способы решения.
3. Задачи третьего уровня предусмотрены для
закрепления способов решения задач предложенных
ранее с добавлением дополнительных вычислений
(объема и процентного отношения).
РЕШЕНИЕ ЗАДАЧ
Задачи по теме «СПЛАВЫ»:
УРОВЕНЬ 1
Найдите плотность бронзы, для изготовления
которой взяли 100 г меди и 30 г олова, считая, что
объем сплава равен сумме объемов входящих в него
металлов.
УРОВЕНЬ 2
1. Кусок сплава из свинца и олова массой 664 г
имеет плотность 8,3 г/см3. Определите массу
свинца в сплаве. Принять объем сплава равным
сумме объемов его составных частей.
2. В куске кварца содержится небольшой
самородок золота. Масса куска 100 г, а его
плотность 8 г/см3. Определите массу
золота, содержащегося в кварце. Принять, что
плотность кварца и золота соответственно равны
2,65 и 19,36 г/см3.
УРОВЕНЬ 3
1. Сплав золота и серебра массой 400 г имеет
плотность 14·103 кг/м3. Полагая объем сплава
равным сумме объемов его составных частей,
определите массу, объем золота и процентное
содержание его в сплаве.
2. В чистой воде растворена кислота. Масса
раствора 240 г, а его плотность 1,2 г/см3.
Определите объем кислоты в растворе и его
процентное содержание, если плотность кислоты 1,8
г/см3. Принять объем раствора равным сумме
объемов его составных частей.
Выходной контроль:
Установите соответствие:
Ответы: 1-Д, 2-Ж, 3-А, 4-Б, 5-В. 6-Г, 7-Е.
Домашнее задание:
Дополнительный материал.
Сплавы различаются по своему предназначению.
Конструкционные сплавы: стали, чугуны,
дюралюминий.
Конструкционные со специальными свойствами
(например, искробезопасность, антифрикционные
свойства): бронзы, латуни.
Для заливки подшипников: баббит.
Для измерительной и электронагревательной
аппаратуры: манганин, нихром.
Для изготовления режущих инструментов:
победит.
Подготовьте сообщение о каком-нибудь сплаве.
Расскажите о веществах, которые в него входят, о
их процентном вхождении в сплав и т.д.
Задачи:
1. Найдите плотность стали (сталь —
деформируемый (ковкий) сплав железа с углеродом),
для изготовления которой взяли 100 г железа и 2 г
углерода (углекислого газа), считая, что объем
сплава равен сумме объемов входящих в него
веществ.
2. Чтобы получить латунь, сплавили куски меди
массой 178 кг и цинка массой 355 кг. Какой плотности
была получена латунь? Объем сплава равен сумме
объемов его составных частей.
3. Сплав золота и серебра массой 500 г имеет
плотность 11 г/см3. Полагая объем сплава равным
сумме объемов его составных частей, определите
массу, объем золота и процентное содержание его в
сплаве.
Ответы: 1. 0,098 г/см3, 2. 8540 кг/м3, 3. 50 г, 2,59
см3, 10%.
Подведение итогов урока. Рефлексия
На полях рабочей тетради изобрази схематически
один из рисунков, который соответствует степени
усвоения материала на уроке. Солнце – мне все
понятно, туча – материал интересный, но надо еще
поработать, луна – я все проспал.

Литература
- Материалы курса «Как научить решать задачи по
физике (основная школа). Подготовка к ГИА: лекции
1-4. – М.: Педагогический университет «Первое
сентября», 2010. -80с. - Сборник задач по физике: Учеб. Пособие для
учащихся 7-8 классов средней школы. – 6-е изд.,
перераб. – М.: Просвещение, 1994. – 191 с.: ил. - Физическая олимпиада в 6-7 классах средней школы:
Пособие для учащихся. – 2-е изд, перераб. И доп. –
М.: Просвещение, 1987. – 192 с: ил.
Как вычислить массу определённого вещества в сплаве?
Russian Gun
Ученик
(111),
на голосовании
13 лет назад
По физике задача. Сплав из меди и серебра. Нужны формулы по вычислению массы каждого вещества в теле
Голосование за лучший ответ
Костянтин Анавіщо
Ученик
(223)
13 лет назад
Нужно знать процентное соотношение веществ выраженое в объеме или в массе. Более конкретно ставь вопрос.
никита вострухин
Гуру
(3657)
13 лет назад
Для сплава должна быть указана массовая доля компонентов сплава в %.
С (%масс) = m*100/M (где m – масса компонента, М – масса сплава).
Иван Васильевич меняет профессию
Оракул
(69839)
13 лет назад
В обозначении сплава указаны процентные содержания металлов.
Похожие вопросы
При решении задач на сплавы и смеси считают, что сумма масс сплавляемых веществ равна массе получаемого сплава, что сумма масс вещества, входящего в сплавы равна массе этого вещества в полученном сплаве. Аналогичное допущение принимаем и для сумм масс (объёмов) при смешивании жидкостей.
Рассмотрим подготовительную задачу.
Задача 1. Имеется уксусный раствор массой 1,5 кг, содержащий 40 % уксуса. Сколько килограммов воды нужно добавить в раствор, чтобы новый раствор содержал 10 % уксуса?
Решение. I способ.
1) 40 : 10 = 4 (раза) — во столько раз уменьшилась концентрация уксуса в растворе и увеличилась масса раствора,
2) 1,5 * 4 = 6 (кг) — масса нового раствора,
3) 6 – 1,5 = 4,5 (кг) — воды надо добавить.
II способ. 1) 0,4 * 1,5 = 0,6 (кг) — масса уксуса в первом растворе.
2) Пусть добавили x кг воды. Составим уравнение:
0,1(1,5 + x) = 0,6.
Оно имеет единственный корень 4,5. Значит, надо добавить 4,5 кг воды.
Ответ. 4,5 кг.
Рассмотрим способы решения задач на смеси и сплавы из сборников вариантов для подготовки к ЕГЭ.
Задача 2. (2017) В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
Задача 3. (2018) Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение. Пусть масса первого сплава x кг, второго (150 – x) кг, третьего — 150 кг. Найдём массу никеля в каждом из трёх сплавов. Никеля было
в первом сплаве 0,25x кг,
во втором — 0,3(150 – x) кг,
в третьем — 0,28 *150 = 42 (кг).
Составим уравнение:
0,25x + 0,3(150 – x) = 42.
Решив уравнение, получим его единственный корень x = 60. Теперь ответим на вопрос задачи. Масса первого сплава 60 кг, масса второго сплава 90 кг, первая меньше второй на 30 кг.
Ответ. На 30 кг.
Задача 4. (2019) Первый сплав содержит 5 % меди, второй — 14 % меди. Масса второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Решив уравнение, получим его единственный корень x = 28. При x = 28 масса третьего сплава 2x + 7 равна 63 кг.
Ответ. 63 кг.
Задача 5. (2017) Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?
Решение. Пусть масса первого раствора x кг, второго y кг. Приравняв массы кислоты до смешивания и после смешивания, составим два уравнения:
0,7x + 0,6y = 0,5(x + y + 2),
0,7x + 0,6y + 0,9*2 = 0,7(x + y + 2).
Решив систему этих двух уравнений, получим её единственное решение:
x = 3, y = 4. Использовали 3 кг 70 %-го раствора кислоты.
Ответ. 3 кг.
Задача 6. (2017) Имеется два сосуда. Первый содержит 100 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 28 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Для второго смешивания возьмём 1 кг первого раствора и 1 кг второго, получим 2 кг смеси. Составим первое уравнение:
Решив систему уравнений (1) и (2), получим её единственное решение: x = 12, y = 60. В первом сосуде содержится x * 100 / 100 = 12 (кг) кислоты. Ответ. 12 кг.
Для самостоятельного решения
7. Имеется 400 г морской воды, содержащей 4 % соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?
8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
10. (2017) Имеется два сплава. Первый содержит 5 % никеля, второй — 20 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
11. (2017) Первый сплав содержит 5 % меди, второй — 11 % меди. Масса второго сплава больше массы первого сплава на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
12. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
13. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
Ответы. 7. 400 г. 8. 16 %. 9. 4,8 %. 10. На 75 кг. 11. 6 кг. 12. 5 : 2. 13. 5 : 2.
Для работы с задачами в классе можно использовать вариант заметки в виде презентации: Сплавы и смеси. Задачи 11 из ЕГЭ.
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
