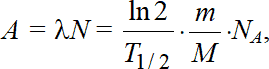Как найти массу во время полураспада

Как правильно решать задачи на закон радиоактивного распада

Реакции первого порядка

Задача 67.
При лечении онкологических заболеваний в организм пациента вводят препарат, содержащий радиоактивный изотоп. Считая радиоактивный распад реакцией первого порядка, определить какая часть радионуклида останется в организме больного через 30 суток, если период полураспада составляет 130 суток.
Решение:
По истечении периода полураспада масса радиоактивного материала уменьшается в два раза. Поэтому количество периодов полураспада вещества будет равно n = (30/130). Поэтому, после n периодов полураспада через 30 суток в организме останется следующая часть радионуклида:

 (1/2)n = (1/2)(30/130) = (1/2)0,231 = 0,852 или 85,2%.

Ответ: останется 85,2% радионуклида.
 

---

Задача 66.
Найти массу радиоактивного материала через промежуток времени, равный четырем периодам полураспада. Начальная масса материала составляла 60 г.
Решение:
По истечении периода полураспада масса радиоактивного материала уменьшается в два раза. Поэтому, после четырех периодов полураспада масса материала будет составлять: 

(1/2)4 = 1/16

от первоначального количества. Следовательно, через заданный промежуток времени масса вещества будет равна: 

m(конечн.) = (1/16 ^. m(нач.) = 1/16 ^. 60 = 3,75 г.

Ответ: m(конечн.) = 3,75 г.
 

---

 
Задача 68.
Период полураспада некоторого вещества 3 недели. Через какое время количество нераспавшихся ядер уменьшится в 16 раз. 
Дано:
T = 2 недели;
N = 1/16 ^. N0;
t = ?
Решение:
Так как N = N0 ^. 2(-t/2);
(1/16 ^. N0) = N0 ^. 2(-t/2);
1/2(4) = 2(-t/2);
-4 = -t/2;
t = (-4) ^. (-2) = 8 недель.

Ответ: t = 8 недель.
 

---

Задача 69.
Какая доля от большого количества радиоактивных ядер остаётся нераспавшейся через интервал времени, равный пяти периодам полураспада?
Решение:
Для расчета нераспавшейся доли радиоактивных ядер используем уравнение: N = N0 ^. 2(-t/Т), где
N0 – количество радиоактивных ядер в произвольно выбранный начальный момент времени t = 0, N – количество радиоактивных ядер, не распавшихся к моменту времени t, Т – период полураспада. 

Учитывая, что t = 4T получим:

N = N0 ^. 2(-4t/Т);
N = N0 ^. 2(-4) = 100% ^. 1/23 = 100% ^.1/16 = 6,25%.

Ответ: 6,25%.

---

Недавно проводил очередные занятия по физике со своими учениками и заметил некоторые трудности в решении задач на радиоактивный распад. По моим наблюдениям в школе и в интернете разбираются самые тривиальные задачи на распад. Задачи из ЕГЭ бывают немного сложнее. Но для интереса я добавил в статью разборы еще 6 задач, которые смело можно назвать задачами «со звёздочкой*», то есть повышенной сложности. На написание теории и подробные решения было потрачено много времени, поэтому, если Вам понравится статья, поддержите своей активностью.

💡 Крупные статьи я выкладываю в pdf в своём канале в telegram Репетитор IT mentor. Подписывайтесь, там публикуется контент, которого на Дзен не будет.

Прежде всего хотелось бы сделать замечание. Для успешного решения задач по физике (в целом, любых задач) Вам понадобятся:
◼ 1. Уверенные знания в математике на уровне физ-мат лицея (это минимум)
◼ 2. Базовые знания по дифференциальному и интегральному исчислению, а также умение применять начальные условия (НУ) и граничные условия (ГУ).
◼ 3. Понимание ограничений и сути процесса ( у вас не должны получаться отрицательная масса или отрицательное время, дробное количество, околосветовые скорости макроскопических объектов )
◼ 4. Хорошее воображение, 3D-видение эксперимента у себя в голове, а также возможность представить как выглядит график функции, описываемой в определенном законе (например: закон радиоактивного распада).
◼ 5. Умение разбивать большую задачу на малые подзадачи (например: определить амплитуду колебаний изображения математического маятника — у вас две задачи: механическая и оптическая — решайте их отдельно, потом сшивайте).
◼ 6. Чувствуйте абстракции. Вы никогда не решите задачу, если попытаетесь учесть всё. Пример: определите траекторию полёта камня, брошенного под углом к горизонту с учётом… эффекта Магнуса, динамического сопротивления ветра, фазы Луны, функции плотности воздуха, динамики вихрей потоков воздуха, распада вещества, из которого состоит камень, термодинамического расширения камня. Сложно? Вот поэтому чувствуйте абстракции.
◼ 7. Программирование. Да… внезапно. Для физики полезно знать какой-нибудь язык программирования. Попробуйте решенную задачу замоделировать и закодить в виде графической анимации. Так ваши решения станут куда более интересными и наглядными. А меняя входные параметры, вы станете лучше понимать поведение физических систем.

Основные определения

Радиоактивность – свойство некоторых нуклидов подвергаться радиоактивному распаду.

Радиоактивность – превращение одних атомных ядер в другие ядра, сопровождающееся испусканием различных частиц и электромагнитного излучения. На латыни radio – излучаю, activus – действенный.

Радиоактивность – самопроизвольное превращение неустойчивых изотопов одного химического элемента в изотоп другого элемента, сопровождающееся испусканием элементарных частиц, ядер и жесткого электромагнитного излучения.

Нуклид – разновидность атома, характеризуемая числом протонов и нейтронов, а в некоторых случаях энергетическим состоянием ядра.

Радионуклид – нуклид, испускающий ионизирующее излучение.

Радиация или ионизирующее излучение – это частицы или гамма-кванты, энергия которых достаточна велика, чтобы при воздействии на вещество создавать ионы и катионы (т.е. ионизировать молекулы на своём пути).

Ионизирующее излучение – поток заряженных или нейтральных частиц и квантов электромагнитного излучения, прохождение которых через вещество приводит к ионизации и возбуждению атомов или молекул среды. По своей природе делится на фотонное (гамма-излучение, тормозное излучение, рентгеновское излучение) и корпускулярное (альфа-излучение, электронное, протонное, нейтронное, мезонное).

Теория для решения задач

Закон радиоактивного распада – закон, который описывается зависимость интенсивности радиоактивного распада от времени и от количества радиоактивных атомов в образце. Закон был открыт Фредериком Содди и Эрнестом Резерфордом. Оба получили Нобелевскую премию. Они обнаружили закон экспериментальным путем. Ещё в далеком 1903 году в работах «Сравнительное изучение радиоактивности радия и тория» этот закон формулировался:

Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии.

То есть скорость превращения всё время пропорционально количеству элементов, ещё не подвергнувшихся превращению.

Данную формулировку можно записать в виде дифференциального уравнения: dN/dt = – λ·N, где dN – изменение количества ядер за время dt.

Это изменение отрицательно, потому что при распаде уменьшается количество оставшихся элементов. Опытным путем было установлено, что эта скорость распада dN/dt пропорционально количеству оставшихся ядер N и некоторой постоянной λ, которая называется постоянной распада и характеризует вероятность радиоактивного распада за единицу времени (имеет размерность 1/c). Данное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными. Решение подобных уравнений можно найти в любом учебнике по высшей математике.

В итоге решение будет иметь вид N = N₀ · exp(- λ·t) :

Отсюда видно, что число радиоактивных атомов какого-либо вещества уменьшается со временем по экспоненциальному (показательному) закону. Помимо постоянной распада λ используются другие характеристики.

Среднее время жизни

Зная закон распада, можно посчитать среднее время жизни радиоактивного атома. Вспоминаем, что dN обозначает количество атомов, которое распадется за время от t до t + dt. Тогда среднее время можно будет найти подобно тому, как мы ищем среднее или математическое ожидание случайной непрерывной величины:

В вычислениях была использована формула для интегрирования по частям. Теория интегрирования также описана в любой книге с конспектами по высшей математике (или математическому анализу, или интегральному исчислению).

Подставим результат для тау (время жизни τ) в экспоненциальную зависимость в формуле распада:

Отсюда видно, что за среднее время жизни τ число радиоактивных атомов образца ( а также его активность – количество распадов в секунду) уменьшается в e ≈ 2.718 раз.

Период полураспада

И всё же большей популярностью пользуется другая характеристика для радиоактивных элементов. Называется она периодом полураспада T. Если немного подумать, то из названия понятно, что это время, в течение которого количество радиоактивных атомов исходного элемента уменьшается в 2 раза. Выведем связь этой величины с постоянной распада:

A – массовое число (число нуклонов в составе ядра атома)
Z – атомный номер в таблице Менделеева (число протонов в ядре)
Для нейтрального атома:

Законы сохранения в распадах

При радиоактивном распаде сохраняются следующие параметры:

1. Заряд. Электрический заряд не может создаваться или исчезать. Общий заряд до и после реакции должен сохраняться, хотя может по-разному распределяться среди различных ядер и частиц. Единичный положительный и отрицательный заряды нейтрализуют друг друга. Аналогично, возможно для нейтральной частицы (типа нейтрона) произвести один заряд каждого знака.
2. Массовое число или число нуклонов. Число нуклонов после реакции должно быть равно числу нуклонов до реакции.
3. Общая энергия. Кулоновская энергия и энергия эквивалентных масс должна сохраняться во всех реакциях и распадах.
4. Импульс и угловой момент. Сохранение линейного импульса ответственно за распределение кулоновской энергии среди ядер, частиц и/или электромагнитного излучения. Угловой момент относится к спину частиц.

Потенциальная энергия взаимодействия α-частицы и остаточного ядра с зарядом Z·e

Вид волновой функции можно получить из решения уравнения Шредингера для взаимодействия ядра атома и α-частицы. Способы решения можно почитать в книгах по физике вузовского уровня или в книгах по ММФ (методы математической физики). В целом, для понимания вам будет полезна теория решения дифференциальных уравнений из конспектов лекций по высшей математике или конкретно по теме – дифференциальное и интегральное исчисление.

По причинам исторического характера ядро He называют альфа-частицей. Установлено, что многие тяжелые ядра с зарядовым числом Z > 82 (Z = 82 имеет свинец) испытывают радиоактивный распад с испусканием альфа-частицы. В альфа-частице удельная энергия связи больше, чем в тяжелых ядрах, поэтому альфа-распад возможен энергетически. К примеру, образце урана U-238 испускает альфа-частицы с периодом полураспада 4.5 млрд. лет. Самопроизвольно происходит реакция:

Спустя 4.5 млрд. лет половина ядер урана U-238 распадается. Разность масс U-238 и продуктов распада равна энергии 4.2 МэВ. Рисунок выше позволяет получить представление о том, почему происходит альфа-распад. Ea – кинетическая энергия вылетающей альфа-частицы. Первоначально альфа-частицы находится в области I и может быть описана стоячей волной с амплитудой Ψвнутр (волновая функция в данной области пространства). Однако, возможно проникновение сквозь барьер, потому что в области вдали от ядра имеется небольшой «хвост» волновой функции Ψвнеш. Вероятность вылета альфа-частицы в момент её соударения с барьером можно оценить выражением: |Ψвнеш|²/|Ψвнутр|².

Число таких столкновений в 1 секунду приблизительно v/2R, где v – скорость альфа-частицы в области I. Таким образом, вероятность испускания альфа-частицы в единицу времени можно записать так:

В образце, содержащем n ядер, число распадов в секунду (скорость уменьшения n) равна

Отсюда с помощью интегрирования и подстановки начальных условий можно снова получить закон радиоактивного распада:

Можно получить ещё одну формулу для оценки периода полураспада:

Формула иллюстрирует применение квантовой механики для объяснения радиоактивности. Квантовая механика дает исчерпывающее объяснение альфа-распада и других радиоактивных превращений. Природа вероятности интересна тем, что если в силу редкой случайности текущее ядро уцелело на протяжении большого числа периодов полураспада, то эта предыстория абсолютно не влияет на вероятность распада в будущем. Этот же эффект имеет место при бросании монеты. Если у вас пять раз выпал орёл, вероятность шестой раз выпасть орлу остаётся по-прежнему равной 0.5.

Вероятность распада ядер одного вещества всегда одна и та же, независимо от их возраста. Допустим, половина ядер какого-либо изотопа распадается за один год. Какое-то ядро, избежавшее распада в первый год, по-прежнему будет иметь вероятность ½ распасться на протяжении второго года. Если сохранится на протяжении двух лет, то вероятность распада на третий год снова будет ½.

💡 Теперь перейдем к практике и поучимся решать основные задачи. Здесь имеются две задачи из ЕГЭ по физике, но также я добавил более сложные задачи, которые не встречались мне в ЕГЭ, однако встречались в вузовской программе для физиков.

Практика решения задач

Задача 1. Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.

Решение:

Задача 2. После крупной радиационной аварии, произошедшей в 1986 году на Чернобыльской атомной электростанции, некоторые участки местности оказались сильно загрязнены радиоактивным изотопом цезия-137 с периодом полураспада 30 лет. На некоторых участках норма максимально допустимого содержания цезия-137 была превышена в 1000 раз. Через сколько периодов полураспада после загрязнения такие участки местности вновь можно считать удовлетворяющими норме? Ответ округлите до целого числа.

Решение:

Задача 3. Период полураспада элемента 1 в три раза больше периода полураспада элемента 2. За некоторое время число атомов элемента 1 уменьшилось в 8 раз. Во сколько раз за это же время уменьшилось число атомов элемента 2?

Решение:

Задача 4*. Вычислить постоянную распада λ для изотопов радия:
а) ²¹⁹Ra; б) ²²⁶Ra; в) ²³⁰Ra. Чему равна вероятность распада изотопов радия за время t = 1 час ?

Решение:

Задача 5*. При определении периода полураспада короткоживущего радиоактивного изотопа использовался счётчик импульсов. За минуту в начале наблюдения было насчитано Δn₀ = 250 импульсов, а через время τ = 1 час было зарегистрировано Δn = 92 импульса. Чему равен период полураспада данного изотопа?

Решение:

Задача 6*. Известно, что из радиоактивного полония ²¹⁰Po массой m = 2.5 грамм за время t = 32 дня в результате его распада образуется гелий объемом V = 40 см³ при нормальных условиях: p₀ = 10⁵ Па и τ₀ = 273 К. Определить по этим данным период полураспада данного изотопа полония.

Решение:

Задача 7*.Оценить количество тепла, которое выделяет полоний ²¹⁰Po массой m = 1 мг за время, равное периоду полураспада этих ядер, если испускаемые α-частицы имеют кинетическую энергию Wα = 5.3 МэВ.

Решение:

Задача 8*. Пусть в ядре урана ²³⁸U альфа-частица сталкивается с потенциальным барьером 5·10²⁰ раз в секунду и Ψвнеш/Ψвнутр = 10⁻¹⁹.
а) Какова вероятность распада этого ядра в 1 сек ?
б) Каково среднее время жизни этого ядра?

Решение:

Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram

Задача. Определите массу не распавшегося радиоактивного вещества по истечении суток, если вначале его масса была кг. Период полураспада вещества дней.

Решение

Думаем: в задаче рассматривается радиоактивный распад. И единственное, что мы можем о нм сказать, это закон радиоактивного распада.

(1)

• где

Однако, нам задано и необходимо проанализировать не количество элементов, а массу вещества. Связь между ними через химическое количество вещества:

(2)

Решаем: работа с уравнениями вида (1) имеет свою логику. Мы можем домножить правую и левую части уравнения на одну и ту же совокупность переменных. Исходя из (2) домножим на . Получим:

(3)

Считаем: перевод в систему СИ необходим, однако в степени соотношения (3) главное, чтобы время и период полураспада совпадали по размерности. Пусть все параметры будут в днях. Тогда:

(кг)

Ответ: (кг)

Ещё задачи по теме «Закон радиоактивного распада»

Прежде, чем отвечать на ваш вопрос, рассмотрим более простой пример. Вы положили полено весом 1 кг в костер. Через некоторое время в костре от полена осталась кучка пепла весом 50г. Куда подевались 950г полена? Нет ли в этом парадокса? Очевидно, что нет – большая часть вещества полена улетучилась с дымом в виде СО2, СО, и других веществ.

С радиоактивным распадом ситуация очень похожая, хотя и немного более сложная. Уран (для определенности возьмем 238й его изотоп), преимущественно, подвержен альфа-распаду. Спонтанное деление и бета-распад возможны, но маловероятны. При альфа-распаде атом урана превращается в атом тория и альфа-частицу (фактически – атом гелия без электронов, летящий с огромной скоростью). Альфа-частица с атомной массой 4 улетает очень стремительно, и масса общего куска уменьшается. Половина распавшихся ядер раньше весила по 238г/моль, а сейчас 234г/моль.

На первый взгляд, через период полураспада, когда такой трансформации подвергнутся половина атомов урана, 1кг урана превратится в 0.5кг урана, 0.492г тория и 8г улетевших альфа-частиц. Но торий, в свою очередь, тоже подвержен радиоактивному распаду и, что важно, распадается намного быстрее. Если для урана период полураспада – миллиарды лет, то для тория-234 – десятки суток. Полураспад всех последующих продуктов урана проходит намного быстрее, чем для урана и потому к завершению периода полураспада урана практически все участвовавшие в распаде атомы выродятся до стабильного свинца-206.

Так что в результате через четыре с хвостиком миллиарда лет мы получим полкило урана, 433г радиогенного свинца, а где-то по миру будут летать остатки 17 грамм альфа-частиц.

В химии гравиметрия («весовой анализ») является арбитражным аналитическим методом. Какими бы ни были методы анализа, применяемые в настоящее время (сейчас получили распространение физико-химические и физические методы), все они так или иначе, применительно к задачам количественного анализа, сводятся к необходимости использовать некоторые исходные вещества в качестве эталонов. Последние могут быть изготовлены с использованием, в конечном итоге, аналитических весов.

Но в ядерной физике и радиохимии гравиметрический метод совершенно не распространен главным образом вследствие того, что в подавляющем числе радиоаналитических задач (и, тем более, в радиоэкологии) имеют дело с такими массами радиоактивных веществ, которые находятся за пределом чувствительности даже наилучших весов. Тем не менее помимо установления абсолютной активности радионуклидов, что выполняется инструментально, бывает необходимо знать и их массу (концентрацию). Это достигается элементарным расчетом на основе соотношения (1.10):

где m – масса радионуклида (г), M – молярная масса радионуклида (г/моль);

N_A = 6,022045•10²³ моль^-1 – постоянная Авогадро.

Отсюда следует:

. (1.17)

(Здесь активность выражается в беккерелях, а период полураспада в секундах).

По этой формуле можно рассчитать массу, например, одного кюри любого радионуклида. Так, 1Kи ²³⁸ U (T_1/2 = 4,5•10⁹ лет) имеет массу около трех тонн, 1 Kи²²⁶Ra (T_1/2= 1600 лет) – 1 г (это так и должно быть, т.к. один грамм именно этого изотопа радия в свое время был выбран за эталон одного кюри).

В то же время масса короткоживущих радионуклидов, имеющих T_1/2 порядка нескольких лет или суток (не говоря уж о тех, период полураспада которых исчисляется секундами или долями секунды), в аналитическом смысле может оказаться настолько незначительной, эфемерной, почти нереальной, что ей нельзя будет приписать проявление каких бы то ни было макроскопических термодинамически фиксируемых свойств. Иными словами, химические (в общем случае термодинамические) характеристики любой фазы, в которую включается (или ею утрачивается, отдается) радиоактивный микрокомпонент, не могут измениться сколько-нибудь заметным образом, т.к. уровень концентрации этой примеси (выражаемый в процентах или в мольных долях) не более значим, чем уровень любых других практически неустранимых загрязнений, присутствующих даже в самых чистых химических препаратах.

Вот такие массы веществ и соответствующие им концентрации в радиохимической литературе получили название «невесомые количества», «микроколичества», или даже «ультрамикроколичества». А само вещество в таких количествах обычно называют микрокомпонентом.

С явлением радиоактивности (точнее – с экспоненциальным характером ее проявления) связан распространенный паралогизм – убежденность некоторых людей в том, что по истечении десяти периодов полураспада любой радионуклид практически распадается полностью.

Проанализируем справедливость этого утверждения. В соответствии с (1.11): N/N₀ = 2 ^{– n} = 2–¹⁰ = 1/1024. При этом распалось (N₀ – N) атомов:

Nрасп = N₀ – N = N₀ (1–1/1024).

Последнее выражение дает основание для высказывания двух суждений.

1) С одной стороны, 1–1/1024 ? 1, т.е. N_расп ? N₀, что соответствует итогу «радионуклид практически распался весь». Казалось бы, это утверждение в какой-то степени приемлемо, т.к. равенство N_расп ? N₀ выполняется с погрешностью (погрешность вычисления) менее 0,1%, о чем многие проектировщики могут только мечтать.

2) Но, с другой стороны, из того факта, что значение некоторой физической величины уменьшилось на три порядка, вовсе не вытекает следствие, что данную величину можно приравнять нулю. Это всего лишь «психологический софизм», поскольку здесь соединились два независимых сравнения, причем одно в процессе рассуждений подменяется другим.

В первом случае признается имеющим смысл фраза, что «0,00098 гораздо меньше (пренебрежимо меньше) единицы». Но и во втором случае оставшееся число атомов, N, тоже необходимо сравнить с каким-то другим эталоном, репером, нормой и т.п., но отнюдь не с единицей.

Скорей всего N и A, которые «остались» (N_ост и A_ост) после истечения 10 T_1/2, нужно сравнивать с существующими нормами или потребностями. Если оценивается вредная сторона носителя радиоактивности, то сравнение должно происходить, например, с санитарными нормами (A_н). Здесь возможны различные ситуации:

A_н > A_ост и даже A_н >> A_ост, либо наоборот A_н<A_ост, A_н << A_ост (обычно в подобных сравнениях фигурируют удельные величины). Понятно, что житейские и юридические выводы, следующие отсюда, будут абсолютно различными. При этом совсем не исключено, что соотношение A_н << A_ост может оставаться в силе не только по истечению 10 T_1/2, но и после прошествия гораздо большего отрезка времени.

Таким образом, психологическому аспекту экспоненциальной зависимости редко отдают должное, она таит в себе ряд паралогизмов и не вписывается в интуицию человека. Эта зависимость наглядна только при сравнении ее с некоторым соответствующим пределом (нормой, репером, эталоном и т.п.).

У закона радиоактивного распада как у зависимости экспоненциального характера есть еще одна особенность, касающаяся временного поведения долгоживущих радионуклидов. В связи с этим рассмотрим один характерный пример.

Период полураспада урана-238 равен 4,5·10⁹ лет. Какова убыль его активности вследствие распада за конкретный, но незначительный по сравнению с периодом полураспада интервал времени, например, за миллион лет?

Эта убыль, выражаемая в долях единицы, отнесенная к начальному значению активности, равна:

Положим t = 10⁶ лет и преобразуем равенство следующим образом:

Обоснованно полагая ? величиной очень малой в сравнении с единицей, ограничимся первым линейным членом разложения логарифмической функции в ряд: ln(1 – ?) ? – ? . Тогда ? = (0,692•10⁶/4,5·10⁹) = 1,5 · 10–⁴ или 0,015%. Таким образом, активность урана-238 как функция времени может быть независимо рассмотрена в двух временных масштабах.

1) В геохронологическом масштабе времени (отрезки времени, сопоставимые, например, с возрастом Земли, признаваемым в космогонии) этот радионуклид значимо изменял свою активность. Так, если возраст Земли в настоящее время оценивается величиной порядка нескольких миллиардов лет, то с момента возникновения нашей планеты как тела Солнечной системы до наших дней активность содержащегося в геосфере урана-238 уменьшилась практически вдвое.

2) В технологическом (антропном) масштабе (отрезки времени, сопоставимые с интервалом, протекшим с момента возникновения Homo Sapiens, и гораздо меньшие), как только что было показано выше, активность этого радионуклида (и, естественно, всех других, обладающих такими же значительными периодами полураспада) может быть рассматриваема как практически независимая от времени: . Это, разумеется, парадоксальный вывод, сбивший с толку даже Фредерика Содди, но он вполне объясним, если не забывать об иерархии масштабов времени, всегда принимаемой во внимание в естествознании.

Иными словами, обсуждение зависимости активности долгоживущих радионуклидов от времени имеет смысл и сопряжено с практически полезными расчетами только тогда, когда четко определен масштаб времени, в соответствии с которым это обсуждение проводится.

Данный текст является ознакомительным фрагментом.