Как найти массу земли по формуле

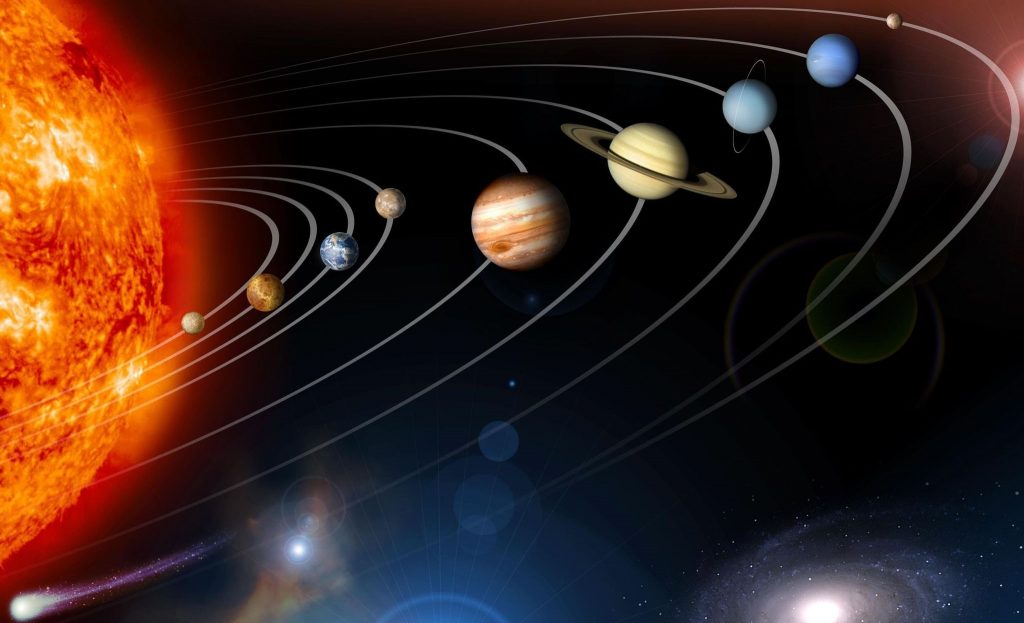
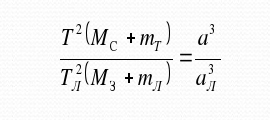Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?

Занимательная физика

Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.

Барометр и законы Ньютона

Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).

F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.

Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.

Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².

Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.

Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.

Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.

Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.

Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.

G = 6,67430(15)*10ˆ(-11) Н·м²·кг²

Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг.

Нейтрино

Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.

Испанские физики поставили лабораторию на Южном полюсе, дождались момента, когда Солнце окажется на Северном полюсе и выловили нейтрино с обратной стороны.

Эксперимент кажется фантастичным, однако измерив скорость частиц, прошедших сквозь Землю, физики нашли плотность планеты и, соответственно, массу.

Как измеряются далекие планеты?

Масса далеких планет вычисляется примерно. Основами для вычислений становятся орбиты планет, орбиты их спутников и гравитационные возмущения между ними.

Масса звезд вычисляется по степени их яркости. Считается, чем ярче небесное тело, тем оно массивнее. По светимости звезды определяется её химический состав, а значит примерная плотность и вес.

Как определить массу Земли по формуле

Определение массы Земли – это одна из фундаментальных задач в физике. Эта величина играет важную роль в различных областях науки, включая астрономию, космологию и геологию. Масса Земли определяется на основе ее гравитационного поля и движения тел в этом поле.

Формула определения массы Земли

Формула определения массы Земли основывается на законе всемирного тяготения Ньютона:

F = G * ((m1 * m2) / r^2)

где:

• F – сила гравитации между двумя телами;
• G – гравитационная постоянная;
• m1 и m2 – массы двух тел;
• r – расстояние между телами.

Для определения массы Земли используется следующая формула:

M = r^2 * ((v^2 * r) / G)

где:

• M – масса Земли;
• r – среднее расстояние Земли от Солнца;
• v – скорость Земли в ее орбите вокруг Солнца;
• G – гравитационная постоянная.

Таким образом, для определения массы Земли необходимо знать три параметра: среднее расстояние Земли от Солнца, скорость Земли в ее орбите вокруг Солнца и гравитационную постоянную.

Как измерить параметры для рассчета массы Земли

Для определения массы Земли необходимо измерить следующие параметры:

• Среднее расстояние Земли от Солнца. Это значение составляет около 149,6 миллионов километров. Оно может быть измерено с помощью радарной астрономии или методом транзитов внешних планет.
• Скорость Земли в ее орбите вокруг Солнца. Это значение составляет около 29,78 километров в секунду. Оно может быть измерено с помощью радарной астрономии или методом лазерного дальномера.
• Гравитационная постоянная. Это значение составляет 6,67430(15) * 10^-11 м^3 / (кг * с^2). Оно было определено экспериментально на Земле.

Измерения параметров для рассчета массы Земли – это сложная и трудоемкая задача. Однако благодаря достижениям современной науки, эту задачу можно решить с высокой точностью.

Итог

Определение массы Земли является важной задачей в физике. Для ее решения необходимо знать три параметра: среднее расстояние Земли от Солнца, скорость Земли в ее орбите вокруг Солнца и гравитационную постоянную. Измерения этих параметров могут быть выполнены с помощью различных методов – от радарной астрономии до лазерного дальномера. Решение этой задачи позволяет лучше понять структуру и эволюцию нашей планеты, а также проводить более точные расчеты в различных областях науки.

Как определить массу земли по формуле

Существует множество способов определения массы Земли — величины, которая играет центральную роль в любых расчетах, связанных с космическими явлениями и астрономическими процессами. В этой статье мы рассмотрим один из наиболее точных методов вычисления массы Земли по формуле.

Формула определения массы Земли

Для того, чтобы вычислить массу Земли, необходимо использовать формулу:

М= gR²/G

где:

• М — масса Земли
• g — ускорение свободного падения на поверхности Земли
• R — радиус Земли
• G — гравитационная постоянная

Эта формула основывается на законе всемирного тяготения Исаака Ньютона.

Как получить значения для формулы

Для того, чтобы определить массу Земли, необходимо знать значения ускорения свободного падения на поверхности Земли, ее радиуса и гравитационной постоянной.

Ускорение свободного падения

Значение ускорения свободного падения можно измерить с помощью специального прибора — гравитометра. Также существуют различные таблицы, в которых приводятся значения ускорения свободного падения для разных мест на Земле. В среднем, значение ускорения свободного падения на поверхности Земли составляет примерно 9,81 м/c².

Радиус Земли

Значение радиуса Земли можно получить из геодезических данных — например, с помощью спутниковых измерений. Значение радиуса Земли составляет примерно 6 371 км.

Гравитационная постоянная

Значение гравитационной постоянной G было определено с помощью множества различных экспериментов, включая измерения колебаний маятников вблизи гор и опыты с использованием спутниковых систем. Для вычислений массы Земли используют значение гравитационной постоянной, равное 6,67430(15) * 10^-11 м³/кг*с².

Расчет массы Земли

Подставив значения ускорения свободного падения, радиуса Земли и гравитационной постоянной в формулу, можно получить значение массы Земли:

М= 9,81 м/с² * (6 371 км)² / (6,67430 * 10^-11 м³/кг*с²) ≈ 5,97 * 10²⁴ кг

Таким образом, наша планета имеет массу, приблизительно равную 5,97 * 10²⁴ кг.

Общий итог

Определение массы Земли необходимо при проведении многих астрономических и космических расчетов. Формула, основанная на законе всемирного тяготения Исаака Ньютона, позволяет определить массу Земли с высокой точностью. Для ее вычисления требуются знания значений ускорения свободного падения, радиуса Земли и гравитационной постоянной. Полученное значение массы Земли является одним из наиболее точных и используется в различных областях науки и техники.

Как определить массу земли по формуле

Изучение и научное исследование планеты на которой мы живем — это одна из главных задач для астрономов и ученых нашего времени. Одной из таких важных задач является определение массы Земли. Окончательное число является ключевым параметром для науки и компьютерных моделей, которые используются для изучения нашей планеты и ее окружения.

Формула для определения массы земли

Существует несколько способов экспериментального определения массы земли, но самый точный метод, который используют современные астрономы, это определение массы Земли по формуле Ньютона. Для этого используются параметры, которые были получены из точнейших измерений гравитационного притяжения Земли:

F = G * (M1 * M2) / r^2

• F — сила гравитационного притяжения между двумя телами
• G — гравитационная постоянная, значения которой известны
• М1 — масса одного тела (Земли)
• М2 — масса другого тела (например, тестового тела)
• r — расстояние между центрами масс двух тел

Наблюдения показали, что вектор гравитационной силы, действующей на объект, направлен к земной поверхности, поэтому земля рассматривается как точечный объект. Это — одна из важных гипотез, которая позволяет объяснить форму фигуры земли и приводит к средней плотности Земли, которую мы знаем сегодня.

Как определить параметры для формулы

Существует несколько способов определения параметров, необходимых для формулы. Один из самых точных — это размещение двух тел на известном расстоянии друг от друга и измерения силы притяжения между ними. В настоящее время высокоточные измерения массы Земли осуществляются за счет использования спутников: специальных аппаратов, орбитирующих Землей в конкретной точке в пространстве.

Современные технологии измерения массы Земли, такие как гравитометрия, позволяют получать данные для научных задач с точностью до малых долей процента. Это дает возможность науке разрабатывать более точные компьютерные модели планеты Земля и предсказывать различные ее явления, такие как вулканические извержения, землетрясения, цунами и другие.

Итог

Точное определение массы Земли — это очень важный этап в исследовании нашей планеты и всего окружающего нас пространства. Это позволяет науке разрабатывать более точные и реалистичные компьютерные модели планеты Земля, которые могут помочь предсказывать различные явления и защищать нас от грозящих опасностей. Формула Ньютона, являющаяся основой для определения массы Земли, продолжает положительно влиять на развитие науки и технологии в нашей жизни.

Массу Земли можно измерить при помощи барометра.

В целом мы будем опираться на второй закон Ньютона F=mg и закон всемирного тяготения F=G*m*M/R^2, где F – сила, с которой Земля притягивает барометр, G – гравитационная постоянная, m – масса барометра, M – искомая масса Земли, R – радиус Земли.

В этих обозначениях масса Земли вычисляется по формуле M = g*R^2/G. Осталось только найти величины в правой части формулы.

Сначала измерим ускорение свободного падения g. Для этого нужно сбросить барометр с высокой башни и засечь время падения. Высоту башни, кстати, тоже можно измерить с помощью барометра, но этот вопрос выходит за рамки лекции.

Следующий шаг – определить радиус Земли R. В день летнего солнцестояния, когда Солнце стоит в зените над тропиком рака, нужно измерить длину тени, которую отбрасывает барометр известной нам высоты, находящийся в Москве. Если мы знаем расстояние от Москвы до тропика, то дальше дело техники вычислить радиус Земли.

Самое сложное – вычислить гравитационную постоянную G. Для этого нам потребуется установка, которая называется крутильные весы. Этот прибор позволяет измерить силу, с которой барометр притягивается к тяжёлому свинцовому шару заранее известной массы.

Если мы нигде не схалтурили, мы должны получить значения ускорения свободного падения g=9.8 м/с^2, радиуса Земли R=6371 км и гравитационной постоянной G = 6.67*10^-11 м^3/(кг*с^2).

Следовательно, масса Земли равна примерно 6*10^24 (6 и 24 нуля) килограмм.

Чтобы найти массу других планет, учёные отправляют на эти планеты космонавтов с барометрами.

Источники:

[1] Опыт Галилея со свободным падением: wikipedia.org

[2] Эратосфен и вычисление радиуса Земли: wikipedia.org

[3] Крутильные весы и опыт Кавендиша: wikipedia.org

[4] Второй закон Ньютона: wikipedia.org

[5] Закон всемирного тяготения: wikipedia.org

[6] Измерение высоты здания с помощью барометра: lyceum1502.ru

3,2 K

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 августа 2022 года; проверки требуют 6 правок.

Ма́сса Земли́ (в астрономии обозначается M_⊕, где ⊕ — символ Земли) — масса планеты Земля, в астрономии используется как внесистемная единица массы. 1 M_⊕ = (5,9722 ± 0,0006) × 10²⁴ кг^[1].

Три других планеты земной группы — Меркурий, Венера и Марс — имеют массу 0,055 M_⊕, 0,815 M_⊕ и 0,107 M_⊕ соответственно.
По сравнению с массой других небесных тел масса Земли составляет:

• 81,3 масс Луны;
• 0,00315 массы Юпитера (масса Юпитера составляет 317,83 M_⊕)^[2];
• 0,0105 массы Сатурна (масса Сатурна составляет 95,16 M_⊕)^[3];
• 0,0583 массы Нептуна (масса Нептуна составляет 17,147 M_⊕)^[4];
• 0,00000300349 массы Солнца (масса Солнца составляет 332946 M_⊕).

Формула для определения массы Земли[править | править код]

Согласно закону всемирного притяжения Ньютона сила притяжения между двумя телами:

,

здесь M — масса земли, m — масса произвольного тела на поверхности Земли, R — расстояние между центрами масс (в данном случае это радиус Земли), G — гравитационная постоянная.

С другой же стороны сила тяжести (притяжения тела к Земле) равна:

,

m — масса произвольного тела на поверхности Земли, g — ускорение свободного падения.

Поскольку силы одинаковы, то получаем:

Изменение массы Земли[править | править код]

Масса Земли не является постоянной величиной, и в настоящее время потеря массы превышает прирост^[5]. На величину массы Земли влияют многочисленные факторы.

Факторы, увеличивающие массу Земли:

• Космическая пыль: метеоры, пыль, кометы и т. д., за счёт неё масса Земли возрастает примерно на 40 тысяч тонн в год^[6]

Факторы, уменьшающие массу Земли:

• Диссипация атмосферных газов — водорода (3 кг/сек, или 95000 тонн в год^[7]) и гелия (1600 тонн в год^[8]). Кроме того, часть электронов атомов атмосферных газов улетучивается быстрее, чем сами атомы;
• Искусственные спутники, которые находятся на удалённых орбитах и могут покинуть околоземное пространство (около 65 тонн в год^[9]);
• Уменьшение массы Земли приводит к ослаблению её силы тяжести, и, соответственно, способности удерживать атмосферу;
• Нагрев Земли (за счёт как антропогенных процессов, так и глобального потепления) в сочетании с солнечным излучением может увеличить тепловое движение молекул, что также способствует утечке вещества из атмосферы.

См. также[править | править код]

• Эксперимент Кавендиша

Примечания[править | править код]

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.