Видеоурок: закон Архимеда
Зако́н Архиме́да — закон гидростатики и аэростатики: на тело, погружённое в жидкость или газ, действует выталкивающая сила, численно равная весу объема жидкости или газа, вытесненного телом. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой силой или гидростатической подъёмной силой[1][2] (её не следует путать с аэро- и гидродинамической подъёмной силой, возникающей при обтекании тела потоком газа или жидкости).
Так как сила Архимеда обусловлена силой тяжести, то в невесомости она не действует.
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
где:
Описание[править | править код]
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
Плавание тела. Сила Архимеда (


ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом 



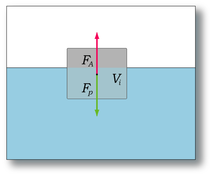
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (

где:
Давление (

где:
Сила давления жидкости или газа на тело определяется разностью сил 

где:
Разница давлений:
В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляцию жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.
Обобщения[править | править код]
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы[править | править код]
Вывод через мысленный эксперимент[править | править код]
Если мысленно заменить погружённое в жидкость тело той же жидкостью, мысленно размещённая в том же объёме порция воды будет находиться в равновесии и действовать на окружающую воду с силой, равной силе тяжести, действующей на порцию воды. Так как перемешивания частиц воды не происходит, можно утверждать, что окружающая вода действует на выделенный объём с той же силой, но направленной в противоположном направлении, то есть с силой, равной 
Расчёт силы[править | править код]
Гидростатическое давление 










При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен 
Вывод через закон сохранения энергии[править | править код]
Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:
где 

По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:
где
— объем погружённой части тела.
Таким образом, для силы Архимеда имеем:
Условие плавания тел[править | править код]
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести 

— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где 

— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнёт плавать.
Примечания[править | править код]
- ↑ Архимеда закон : [арх. 1 января 2023] // Анкилоз — Банка. — М. : Большая российская энциклопедия, 2005. — С. 331. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 2). — ISBN 5-85270-330-3.
- ↑ Архимеда закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 123. — 707 с. — 100 000 экз.
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, к полю, действующему вблизи поверхности планеты).
- ↑ Перышкин А. , Оригинальное доказательство закона Архимеда. Дата обращения: 28 сентября 2020. Архивировано 20 июля 2020 года.
- ↑ Доказательство закона Архимеда для тела произвольной формы. Дата обращения: 28 сентября 2020. Архивировано 21 сентября 2020 года.
- ↑ Buoyancy (англ.). Архивировано 14 июля 2007 года.
Ссылки[править | править код]
- Архимедов закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Закон Архимеда // Энциклопедия «Кругосвет».
Архимедова сила — выталкивающая сила, равная весу газа или жидкости в объёме погружённой части тела.
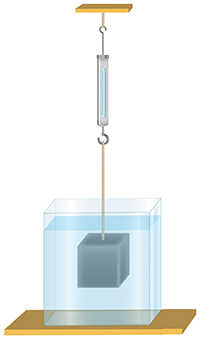
Опыт. Нам понадобятся ёмкость с ручкой и груз в форме цилиндра.
- Растяжение пружины динамометра отметим стрелкой на штативе (рис. (A)), она показывает вес тела в воздухе.
- Подставим сосуд, наполненный жидкостью, до уровня отливной трубки (рис. (B)) и поместим в него цилиндр.
- После погружения цилиндра вода выливается в мерный стакан. Её объём равен объёму цилиндрического груза (рис. (B)).
- Стрелка динамометра поднимается вверх, растяжение пружины уменьшается, что соответствует уменьшению веса тела в жидкости (рис. (C)). В этом случае на цилиндр действует сила тяжести и сила Архимеда, направленная вверх.
- Если в ведёрко вылить вытесненную из отливного стаканчика жидкость, то стрелка динамометра возвратится в начальное положение (рис. (D)).
Вывод: выталкивающая сила, действующая на погружённое в жидкость тело, равна весу жидкости, вытесненной этим телом.
Сила, выталкивающая тело из газа, также равна весу газа, взятого в объёме тела. Это и есть закон Архимеда.
Формулу можно записать в другом виде.
Выразим массу жидкости, вытесняемую телом, через её плотность и объём тела, погружённого в жидкость, тогда получим:
Согласно полученной формуле, на тело, погружённое в жидкость, действует выталкивающая сила (сила Архимеда), равная произведению плотности жидкости, ускорения свободного падения и объёма тела (или той его части, которая погружена в жидкость).
Эта формула позволяет рассчитать выталкивающую силу для тела, находящегося в газе. В этом случае плотность жидкости заменяют плотностью газа.
|
Предположим на дне водоема находится некий объект, который нам необходимо поднять на поверхность. Для расчета толщины металлического троса необходимо знать массу этого объекта. Как можно измерить массу объекта находящегося на дне водоема? Измерить массу тела находящегося на дне водоёма нельзя, её можно только рассчитать. Для этого надо опустить на дно водолаза или батискаф,определить форму тела и произвести измерения его размеров, отрезать небольшой кусок тела, поднять его на поверхность и определить его плотность ρ в кг/дм3, подсчитать, исходя из размеров и формы, объём тела V в дм3. Тогда массу тела m можно рассчитать по формуле m=ρ*V кг. автор вопроса выбрал этот ответ лучшим Sachishin 7 лет назад Массу можно найти по закону Архимеда. F=ρgV. V- объём вытесняемой жидкости,ρ – ее плотность. откуда находим массу вытесненной жидкости m=ρV. А массы вытесненной жидкости будет равна массе тела,погруженного в жидкость RIOLIt 7 лет назад Так не бывает,- в воду падают известные предметы,- автомобиль, так его масса известна, труба- семисотка валяется, тоже- “не бином Ньютона”,( и так далее, и тому подобное…) Грустный Роджер 7 лет назад Масса тела не зависит от того, погружено оно в воду или нет. От этого зависит вес. Поэтому для измерения массы надо просто вынуть тело из воды, высушить его и воспользоваться любыми подходящими весами. Лучше рычажными, а не пружинными. Magnus 7 лет назад Если бы знать, какой конкретно объект вам нужно поднять, можно было бы предложить что-то конкретное, а так… Масса тела, погруженная в воду, равняется произведению его объема на (плотность минус единица). Знаете ответ? |
На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Статьи
Линия УМК А.В. Перышкина. Физика (7-9)
Физика
Закон Архимеда, или Как распознать ложь?
Придворный ювелир изготовил для царя Гиерона золотую корону. Но царь, который не привык никому доверять, попросил Архимеда определить, золотая ли корона на самом деле, или золотых дел мастер подворовывает и подмешал к золоту львиную долю серебра.
Из статьи вы узнаете, сумел ли Архимед вывести лжеца на чистую воду? И что же открыл изобретатель благодаря своим опытам?
02 июля 2019
История открытия
В древних Сиракузах жил инженер, математик и физик по имени Архимед. Образование он получил отличное, изобретения его ценились и в средствах он не нуждался. И периодически к нему обращались сильные мира для решения всяких сложных задач. И одной из таких задач было определить подлинность короны царя Гиерона.
Казалось бы, что в этом сложного?
Используй формулу
ρт = mт / Vт (1).
Раздели mт массу слитка, что был выдан ювелиру на объем короны Vт, получишь плотность короны ρт. Сравни полученный результат с известной плотностью золота, и дело в шляпе. А ювелир получит либо плату за работу, либо близкое знакомство с придворным палачом.
Однако эта формула хорошо работает с объектами простой формы: шар, куб, параллелепипед. А мы то помним, что исследуем корону, у которой множество зубцов, выпуклостей и ажурных плетений.
Как можно определить объем предмета столь сложной формы? Не знаете? Вот и Архимед тоже не знал.

Физика. 7 класс. Учебник
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Долгое время ученый думал над задачей, и в один из дней, в задумчивости опускаясь в наполненную водой ванну, обратил внимание, что часть воды выплеснулась через край. Современники рассказывают, что именно в этот момент Архимед закричал: «Эврика!», что по-гречески значит «Нашел!» и, даже не одеваясь, побежал в царский дворец.
Еще пару дней понадобилось исследователю, чтобы изобрести прибор, с помощью которого он мог бы измерить объем воды, вылившейся при погружении короны. Этот прибор, названный впоследствии ведерком Архимеда, можно увидеть на странице 145 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Затем, с помощью опытов с золотыми и серебряными слитками, доказать, что объем жидкости равен объему слитка, а следовательно будет равен и объему короны. И последним этапом определить плотность короны.
Говорят, что царь был прав в своих подозрениях, и ювелир был нечист на руку. А всю плату, что причиталась за корону мастеру, получил Архимед.
Действие жидкости и газа на погруженное в них тело
Что же открыл Архимед благодаря своим опытам?
Ученый определил некую силу, которая действую в обратном направлении силе притяжения и позволяет предметам плавать в воде и воздухе. Эту силу по праву назвали силой Архимеда или выталкивающей силой.
Определение закона Архимеда: тело погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость.
Формулы
На планете Земля на все предметы действует сила земного притяжения. Для объектов на земной поверхности силу притяжения можно рассчитать по формуле:
Fт = mтg, (2)
где mт — масса тела, а g — ускорение свободного падения, равное 9,8 м/с2.
Когда же объект погружается в жидкость или газ, на него начинает действовать выталкивающая сила или сила Архимеда, которая рассчитывается по формуле:
FА = mжg, (3)
где mж — масса жидкости, вытесненной целым объектом или его частью, находящейся в жидкости.
Массу вытесненной жидкости в свою очередь можно определить используя формулу:
mж = ρжVж, (4)
и соответственно преобразовать формулу закона Архимеда:
FА = ρжVжg. (5)
Как же соотносятся между собой сила тяжести и сила выталкивания. Все просто:
- если сила притяжения больше силы выталкивания, предмет утонет;
- если силы примерно равны — предмет будет плавать в толще жидкости или газа;
- а если сила выталкивания больше силы притяжения, предмет всплывет.
Многочисленные опыты, благодаря которым мы можем пользоваться формулами силы выталкивания, подробно разобраны в § 50 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Несмотря на то, что Архимед впервые открыл силу выталкивания в воде, сила Архимеда характерна также и для газов, и именно благодаря ей смог подняться в воздух первый воздушный шар, а вдохновленный и восхищенный этим событием писатель Жюль Верн написал свой роман «Вокруг света за 80 дней».
А теперь давайте поможем царю решить его задачу с короной.
Предположим, что корона царя Гиерона в воздухе весит 22 Н, а в воде 19,75 Н, вычислите плотность вещества короны.
Как мы узнали в начале статьи, плотность вещества находится по формуле:
ρт = mт/Vт. (1)
Глядя на формулу, понимаем, что для решения задачи нам не известны ни масса короны, ни ее объем.
Из предыдущего курса физики (§ 27 учебника «Физика 7 класс» под редакцией А.В.Перышкина.), помним, что для неподвижного тела вес P равен силе тяжести Fт и рассчитывается по формуле:
P = Fт = mтg, (2)
где g — ускорение свободного падения и его значение равно g = 9,8 Н/кг. Однако, если не требуется большая точность в расчетах, значение можно округлить до 10 Н/кг
-
Зная вес короны в воздухе, мы используя формулу (2) можем найти массу короны.
Pт = Fт = mтg,
-
Мы также знаем, что вес тела в воде отличается от веса тела в воздухе на силу Архимеда.
FA = 22 — 19,75 Н = 2,25 Н
-
Согласно формуле (5) сила Архимеда равна FА = ρжVжg
где ρж = ρводы = 1000 кг/м3
Из нее находим объем вытесненной жидкости и соответственно объем короны
-
Остается финальный штрих: рассчитать плотность.
ρт = mт/Vт
ρт = 2,2 кг / 0,000225 м3 = 9778 кг/м3 или 9,8 г/см3
- сила, с которой Архимед передвигал ванну;
- сила, которая поднимает вверх тело находящееся в жидкости или газе; (+)
- сила мышц Архимеда;
- сила, с которой твердое тело действует на поверхность.
- на тела погруженные только в газ;
- на тела погруженные только в жидкость;
- на тела погруженные в газ или в жидкость; (+)
- на тела находящиеся в невесомости.
- 9,8 м/с3;
- 9,8 Н/кг; +
- 9,8 км/ч;
- 8,9 м/с2.
- растянется больше;
- сожмется; (+)
- не изменится;
- зависит от веса тела.
- на того, кто лучше умеет плавать;
- на того, кто вытеснил больше воды; (+)
- на того, то не умеет плавать;
- на того, кто вытеснил меньше воды.
- FА = ρжVжg; (+)
- FА = ρтVжg;
- FА = ρжVтg;
- FА = mтg.
- взлетит;
- всплывет;
- утонет; (+)
- поплывет.
- бензин; (+)
- вода Мертвого моря;
- оливковое масло;
- чистая вода.
- от плотности жидкости;
- от вытесненного объема жидкости;
- от массы тела; +
- от времени нахождения тела в жидкости.
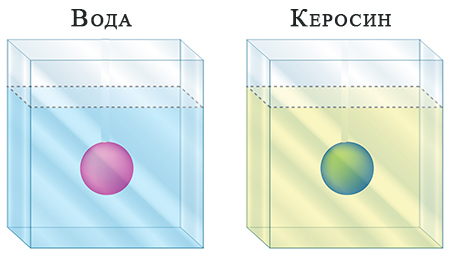
- одинакова, т.к. объем шариков одинаков;
- сила выталкивания больше в емкости с керосином, потому что плотность меньше воды;
- сила выталкивания больше в емкости с водой, потому что ее плотность больше керосина. (+)
Зная, что плотность золота 19,3 г/см3 или 19 300 кг/м3, можем сказать, что корона царя Гиерона сделана из какого-то сплава, но не из чистого золота. Увы, царь был прав, подозревая мастера в нечестности. И мне даже немного жаль нерадивого ювелира. Ведь никто не любит, когда воруют его собственность, а цари особенно.
Теперь попробуйте самостоятельно решить задачу № 5 на странице 147 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Методические советы
Тест «Закон Архимеда»
1. Сила Архимеда это:
2. Сила Архимеда действует:
3. Чему равно ускорение свободного падения g?
4. К пружине подвешено некое тело. Если тело погрузить в емкость с жидкостью, что произойдет с пружиной?
5. Два друга пошли плавать в реке. Один из них при погружении вытесняет объем 60 дм3, второй 40 дм3. На кого из ребят будет действовать большая сила Архимеда?
6. Формула силы выталкивания это:
7. Если сила тяжести больше силы Архимеда, тело:
8. 4 одинаковых стальных шарика погрузили в 4 разные жидкости: чистая вода, вода мертвого моря, бензин, оливковое масло. В какой жидкости сила выталкивания будет наименьшей?
Плотность масла 915 кг/м3, плотность бензина 750 кг/м3.
9. Сила тяжести зависит:
10. В двух емкостях плавают два шарика равного объема. Одинакова ли сила выталкивания?
#ADVERTISING_INSERT#