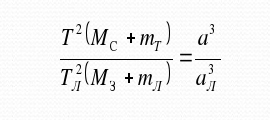Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
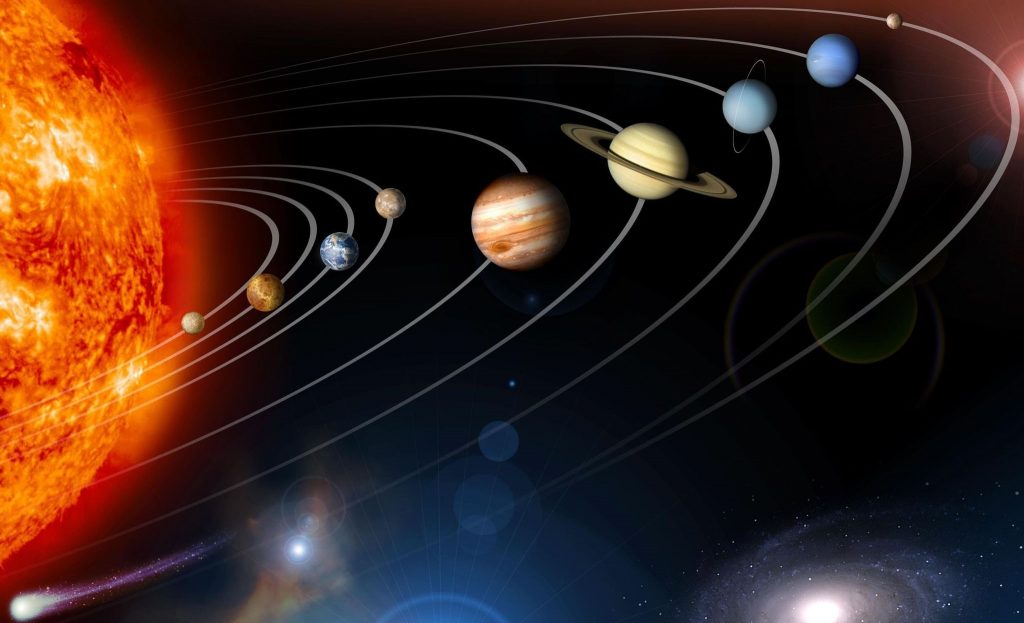
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
Содержание
- Формула массы звезды астрономия
- Что такое масса звезды?
- Формула массы звезды
- Применение формулы массы звезды
- Итог
- Формула массы звезды: измерения и расчеты
- Методы измерения массы звезды
- Формула массы звезды
- Заключение
- Формула массы звезды астрономия
- Что такое масса звезды?
- Как определить массу звезды?
- Формула массы звезды
- Заключение
Формула массы звезды астрономия
Астрономия — одна из самых популярных и интересных наук, которая изучает мир за пределами нашей планеты. Как известно, внутренний мир звезд является одной из самых загадочных тайн для ученых. Теории, связанные с происхождением, эволюцией и исчезновением звезд, рассматриваются на протяжении многих лет. Вычисление массы звезды среди них является одной из самых важных задач. В данной статье рассмотрим формулу массы звезды астрономия и ее применение.
Что такое масса звезды?
Масса звезды — это основной характеристикой звезды, которая может влиять на ее свойства и характеристики. Масса звезды связана с такими параметрами, как ее светимость, радиус и жизненный цикл. Она также играет важную роль в расчетах, связанных с кинематикой звезд.
Вычисление массы звезды является одной из важных задач астрономии. Изучение звездного состава Галактики, создание ее карты, оценка влияния звезд и галактик на космическое пространство, — все это требует знания масс звезд и галактик. Знание массы звезды может иметь прямое практическое значение для ученых-астрономов при поиске и изучении инопланетных группировок, а также поможет понять, каким именно способом формируются звездные скопления в галактике.
Формула массы звезды
Формула массы звезды — это уравнение, которое используется для определения массы звезды на основе измерений ее движения. Эта формула основана на законах гравитации, которые описывают взаимодействие тел.
Масса звезды (M) = 4π² × a³ / G × T²
где:
- M — масса звезды в кг
- a — полуось орбиты звезды в метрах
- T — период обращения звезды в секундах
- G — гравитационная постоянная (6,67 × 10^−11 Н•м²/кг²)
Эта формула основана на законах Кеплера, которые описывают динамику движения планет и звезд в космическом пространстве.
Применение формулы массы звезды
Применение формулы массы звезды может быть полезно для изучения многих аспектов их жизни. Например, масса звезды может помочь понять, каким образом происходит сплавление двух звезд, создавая коллективное скопление звезд. Она также может помочь определить, каким именно образом звезда избавляется от своей огромной массы при завершении своего жизненного цикла.
Вычисление массы звезды также позволяет ученым оценивать размеры искажений пространства-времени, которые создаются по мере того, как крупные звезды со временем погибают. Также она может оказаться полезной при планировании космических миссий, которые связаны с изучением звездного состава Галактики.
Итог
Формула массы звезды астрономия — это ураынение, которое позволяет вычислять массу звезды. Она основана на законах гравитации и Кеплера и может использоваться для изучения жизненного цикла звезды, создания карты звездного состава Галактики и планирования космических миссий.
Формула массы звезды: измерения и расчеты
В космологии и астрономии одним из наиболее важных параметров является масса звезды. Измерение этого параметра может дать нам важную информацию о звезде, такую как ее возраст, радиус, скорость вращения, а также позволяет нам сравнивать звезды между собой и классифицировать их. Существует несколько способов измерения массы звезды, но все они основываются на нескольких основных принципах и формулах.
Методы измерения массы звезды
- Кинематический метод – основан на измерении скорости звезды и ее орбитального периода в двойной системе. Этот метод позволяет измерить массу звезды, определяя ее гравитационное взаимодействие с другой звездой в двойной системе.
- Спектроскопический метод – основан на анализе спектра звезды для измерения ее радиальной скорости. Этот метод также используется для измерения массы звезд в двойной системе.
- Фотометрический метод – применяется для измерения массы звезд на основе их светимости и температуры.
Формула массы звезды
Формула для расчета массы звезды принимает во внимание силу гравитационного притяжения между звездами:
M = (a3/P2) x (4π2/G) x (1/(1+q))2 x q
Где:
- M – масса звезды;
- a – большая полуось орбиты;
- P – период обращения;
- G – гравитационная постоянная;
- q – массовое отношение двух звезд.
Эта формула применяется для измерения массы двойных звезд в системе. Измерительные значения для a и P берутся из орбитальных данных, полученных наблюдением системы.
Однако, существуют другие формулы и методы измерения массы звезды, которые учитывают другие факторы, такие как скорость вращения звезды и радиус. Для измерения массы одиночных звезд также используются методы, которые основаны на стандартных моделях эволюции звезд для определения их массы.
Заключение
Измерение массы звезды является важным параметром в космологии и астрономии, позволяя узнавать много интересной информации как о звезде, так и о галактике в целом. Существуют различные методы измерения массы звезды, но все они основываются на единственной формуле, учитывающей гравитационную силу между звездами. Используя эту формулу, астрономы и космологи могут точно определить массу звезды и использовать это значение для предсказания и изучения свойств звезды и галактики, в которой она находится.
Формула массы звезды астрономия
Астрономия – это одна из наиболее увлекательных и интересных наук, которой увлекаются многие люди по всему миру. Она изучает весь мир и жизнь во всех ее проявлениях, включая звезды и планеты. Одним из ключевых аспектов изучения звезд – это установление их массы.
Что такое масса звезды?
Во время создания звезды огромное количество газа и пыли сходятся в единую точку и начинают сжиматься. При процессе сжатия также совершается способность гравитации. Это означает, что воздействие силы притяжения становится все сильнее и сильнее, пока не начнется ядерный процесс, генерирующий высокую температуру и давление в ядре звезды.
Это тепло и давление позволяют звезде противостоять гравитации и продолжать оставаться в таком же состоянии на протяжении всего жизненного цикла, который варьируется в зависимости от массы звезды.
Поэтому, масса звезды – это ключевой фактор в ее жизненном цикле. Она определяет время жизни и концовку каждой звезды.
Как определить массу звезды?
Существует несколько методов для измерения массы звезды. Один из них – это изучение гравитационного влияния звезд на другие объекты в космосе. Например, когда две звезды сближаются друг с другом, они начинают вращаться вокруг общего центра масс.
Масса можно также измерить, изучая изменения в скорости движения звезды, вызываемые гравитационными воздействиями на другие объекты. Эта информация может быть получена с помощью телескопов в сочетании с собранными данными, которые позволяют установить скорость звезды относительно Земли, а также ее движение в пространстве.
Если вы хотите узнать массу звезды, вы можете также использовать формулу массы звезды.
Формула массы звезды
Формула массы звезды довольно проста и легко запоминается. Ее можно использовать для измерения массы звезды, если известны ее свойства, такие как радиус, кинетическая энергия и температура.
Масса = (константа x радиус x скорость^2) / гравитационная постоянная
Здесь константа – это константа универсального гравитационного соединения, равная 6,674 x 10^-11 m^3 kg^-1 s^-2, радиус определяет радиус звезды, скорость – скорость звезды, а гравитационная постоянная – это фундаментальная константа.
Эта формула позволяет установить массу звезды при известных свойствах. Для большинства людей эта формула может показаться сложной, но даже те, кто далек от астрономии, могут понять ее значение и использование в научном исследовании вселенной.
Заключение
Звезды – это красивые и могущественные объекты, которые вечны. Изучение их свойств и массы позволяет нам лучше понять жизненный цикл звезд, их роль во вселенной и, возможно, найти ответы на многие вопросы о природе мироздания.
Формула массы звезды позволяет астрономам и ученым измерять массу звезды, космические объекты, а также осуществлять многочисленные исследования, которые могут быть применены в практических целях.
Астрономия – это увлекательный мир невероятно красивых звезд, планет и других космических объектов, который остается одним из самых интересных исследовательских областей в науке сегодня.
Среди звёзд, которые видны на небе рядом, различают оптические двойные и физические двойные звёзды. В первом случае такие две звезды хотя и видны вблизи, но находятся в пространстве далеко друг от друга. Если же в результате наблюдений выясняется, что они образуют единую систему и обращаются вокруг общего центра масс под действием взаимного тяготения, то они называются физическими двойными звёздами.
Первым, кто доказал, что такие звёзды действительно существуют, был известный английский астроном Вильям Гершель (1738—1822). Множество двойных звёзд открыл и исследовал В. Я. Струве. В настоящее время известно уже более 70 тыс. этих объектов. Когда число звёзд в системе, связанной взаимным тяготением, оказывается более двух, то их называют кратными. В настоящее время считается, что большинство звёзд (более 70%) образуют системы большей или меньшей кратности. В зависимости от того, каким способом можно обнаружить двойственность звезды, их называют по-разному. Если она заметна при непосредственных наблюдениях в телескоп, то это визуально-двойная звезда. Если же об этом можно судить только по спектру, то это спектрально-двойная звезда.
Редким примером двойной звезды, оба компонента которой различимы даже невооружённым глазом, являются Мицар и Алькор в созвездии Большой Медведицы. Среди ярчайших звёзд также были обнаружены двойные: Сириус, Капелла, Кастор и др. Более того, оказалось, что во многих случаях каждая из звёзд такой пары сама состоит из нескольких звёзд. Так, Мицар и Капелла имеют в своём составе четыре компонента, а Кастор — шесть. Выяснилось, что α Центавра является тройной звездой, одна из которых расположена ближе всего к нам и получила название Проксима (в переводе с греческого «ближайшая»).
У двойных звёзд, каждый компонент которых можно наблюдать в отдельности, периоды обращения вокруг общего центра масс обычно бывают от нескольких лет до нескольких сотен или даже тысяч лет. Их орбиты сравнимы по размерам с орбитами планет-гигантов. Большинство спектрально-двойных звёзд имеют периоды обращения порядка нескольких суток, располагаясь друг от друга на расстоянии 5—7 млн км. Самый короткий из известных периодов составляет всего 2,6 ч.
Несмотря на многочисленность двойных звёзд, достаточно надёжно определены орбиты лишь примерно для сотни из них. При известном расстоянии до этих систем использование третьего закона Кеплера позволяет определить их массу. Сравнивая движение спутника звезды с движением Земли вокруг Солнца, можно написать:




где m1 и m2 — массы компонентов звёздной пары; M1 и M2 — массы Солнца и Земли; T1 — период обращения звёзд; T2 — период обращения Земли; A — большая полуось орбиты двойной звезды; a — большая полуось земной орбиты. Выражая период обращения в двойной системе T в годах (периодах обращения Земли), большую полуось орбиты A в а. е. (расстояниях между Солнцем и Землёй), получаем суммарную массу системы в массах Солнца:
m1 + m2 = A3 : 
Чтобы определить массу каждой звезды, надо изучить движение каждой из них и вычислить их расстояния A1 и A2 (A = A1 + A2) от общего центра масс. Тогда мы получим второе уравнение:
m1 : m2 = A2 : A1.
Решая систему двух уравнений, можно вычислить массу каждой звезды.
У спектрально-двойных звёзд наблюдается смещение (или раздвоение) линий в спектре, которое происходит вследствие эффекта Доплера Напомним, что, согласно этому эффекту, при увеличении расстояния между звездой и наблюдателем длина волны принимаемого излучения увеличивается, поэтому спектральные линии смещаются к красному концу спектра. При уменьшении расстояния длина волны уменьшается, а линии смещаются к фиолетовому концу спектра. . Оно меняется с периодом, равным периоду обращения пары. Если яркости и спектры звёзд, составляющих пару, сходны, то в спектре наблюдается периодическое раздвоение линий (рис. 5.16, а). Пусть компоненты A и B занимают положения A2 или B2, когда один движется по направлению к наблюдателю, а другой — от него. Спектральные линии приближающейся звезды сместятся к фиолетовому концу спектра, а удаляющейся — к красному. Линии в спектре будут раздвоены. В положениях A1 и B1 оба компонента движутся перпендикулярно лучу зрения, и раздвоения линий не наблюдается. Если одна из звёзд настолько слаба, что её линии не видны, то будет наблюдаться периодическое смещение линий более яркой звезды (рис. 5.16, б).
Рис. 5.16. Раздвоение линий в спектре двойной звезды
Для наблюдателя, который находится в плоскости орбиты спектрально-двойной звезды, её компоненты будут поочерёдно загораживать, «затмевать» друг друга. Такие звёзды называют затменно-двойными или алголями — по названию наиболее известной звезды этого типа β Персея. Её арабское название «эль гуль» (дьявол) постепенно превратилось в Алголь. Возможно, что ещё древние арабы заметили странное поведение этой звезды: в течение 2 суток 11 часов её яркость остаётся постоянной, но затем за 5 часов она ослабевает от 2,3 до 3,5 звёздной величины, а за следующие 5 часов её прежняя яркость восстанавливается (рис. 5.17).
Рис. 5.17. Схема затмений и кривая блеска Алголя
В настоящее время известно более 5 тыс. затменно-двойных звёзд. Их изучение позволяет определить не только характеристики орбиты, но также получить некоторые сведения о самих звёздах. Продолжительность затмения даёт возможность судить о размерах звезды. Рекордсменом здесь является ε Возничего, в системе которой при периоде 27 лет затмение продолжается 2 года. Когда во время затмения свет одной звезды проходит через атмосферу другой, можно детально исследовать строение и состав этой атмосферы. Форма кривой блеска некоторых звёзд свидетельствует о том, что их форма существенно отличается от сферической (рис. 5.18). Близкое расположение компонентов приводит к тому, что газы из атмосферы одной звезды перетекают на другую. Иногда эти процессы принимают катастрофический характер, и наблюдается вспышка новой звезды.
Рис. 5.18. Кривая блеска несферической двойной звезды

Определение масс звёзд на основе исследований двойных звёзд показало, что они заключены в пределах от 0,03 до 60 масс Солнца. При этом большинство из них имеют массу от 0,3 до 3 масс Солнца. Очень большие массы встречаются крайне редко.
Методы изучения спектрально-двойных и затменно-переменных звёзд в настоящее время используются также для поиска планет, обращающихся вокруг других звёзд (экзопланет). К концу 2009 г. было подтверждено открытие около 400 экзопланет, которые составили 340 планетных систем. В их числе было 42 системы, содержавшие не менее двух планет, а одна — не менее 5. Большинство этих планет оказались газовыми гигантами типа Юпитера и Сатурна.
Теперь усилия учёных направлены на поиски планет, которые по своим размерам и массе похожи на Землю и находятся недалеко от звёзд, что обеспечило бы на поверхности планеты условия, необходимые для существования жизни. С этой целью был запущен КА «Кеплер», на котором установлен фотометр, чувствительность которого составляет 10–5. Он позволяет заметить ослабление потока света от звезды, вызванное прохождением планет по её диску, всего лишь на одну стотысячную его долю. «Кеплер» исследовал свыше 52 тыс. звёзд в небольшой области неба между созвездиями Лебедя и Лиры. За 2 года работы было найдено более 2300 звёзд, у которых подозревается наличие планет. В 246 случаях это могут быть планеты, которые по размерам сравнимы с Землёй. Ещё не для всех заподозренных случаев получено окончательное подтверждение наличия планет. Однако даже эти предварительные результаты позволяют надеяться, что число экзопланет в нашей Галактике окажется больше, чем считалось ранее. Об этом говорит и открытие 2016 г.: планета с массой всего в 1,3 массы Земли была открыта у ближайшей к Солнцу звезды — Проксимы Центавра.
Рис. 5.19. Пятна на диске Бетельгейзе
К сожалению, звёзды расположены так далеко от нас, что за редким исключением они даже в самые мощные телескопы видны как точки. Лишь в последние годы для некоторых самых крупных из них удалось получить изображение в виде диска, на котором обнаруживаются пятна (рис. 5.19).
В большинстве случаев размеры звёзд приходится рассчитывать на основе данных об их светимости и температуре. Светимость звезды рассчитывается по той же формуле, что и светимость Солнца:
L = 4πR2σT 4.
Отношение светимостей звезды и Солнца будет равно:


Приняв, что R☉ = 1 и L☉ = 1, получаем выражение для вычисления радиуса звезды (в радиусах Солнца):
R = 

Результаты этих вычислений достаточно хорошо согласуются с данными непосредственных измерений с помощью интерферометра размеров наиболее крупных звёзд, расстояния до которых невелики.
Рис. 5.20. Солнце в сравнении с гигантами и сверхгигантами
Рис. 5.21. Размеры звёзд-карликов
Звёзды самой большой светимости (сверхгиганты) действительно оказались очень большими. Красные сверхгиганты Антарес и Бетельгейзе в сотни раз больше Солнца по диаметру (рис. 5.20). Зато диаметр красных карликов, относящихся к главной последовательности, в несколько раз меньше солнечного. Самыми маленькими звёздами являются белые карлики, диаметр которых составляет несколько тысяч километров (рис. 5.21).
Расчёты средней плотности звёзд различных типов, проведённые на основе имеющихся данных об их массе и размерах, показывают, что она может значительно отличаться от средней плотности Солнца. Так, средняя плотность некоторых сверхгигантов составляет всего 10–3 кг/м3, что в 1000 раз меньше плотности воздуха при нормальных условиях. Другой крайностью является плотность белых карликов — около 109 кг/м3.
В зависимости от массы и размеров звёзды различаются по внутреннему строению, хотя все имеют примерно одинаковый химический состав (95—98% их массы составляют водород и гелий).
Звёзды главной последовательности, температура которых такая же, как у Солнца, или ниже, похожи на него по внутреннему строению. Среди множества звёзд этого типа есть и такие, которые по многим своим характеристикам являются «двойниками» Солнца. Наиболее яркой из них является β Гончих Псов. У более горячих звёзд главной последовательности внешняя конвективная зона отсутствует. В этих звёздах конвекция происходит в ядре протяжённостью до 1/4 их радиуса, окружённом лучистой оболочкой (рис. 5.22).
Рис. 5.22. Внутреннее строение звёзд различных классов
Гиганты и сверхгиганты имеют очень маленькое ядро (его радиус около 0,001 доли радиуса звезды). Термоядерные реакции происходят в окружающем его тонком слое; далее на протяжении около 0,1 радиуса звезды происходит передача энергии излучением. Практически весь остальной объём (9/10 радиуса) составляет протяжённая конвективная зона. Белые карлики состоят из вырожденного газа, давление которого определяется лишь его плотностью и не зависит от температуры. Равновесие такой «экзотической» звезды, масса которой равна солнечной, наступает лишь тогда, когда она сожмётся до размеров, примерно равных размерам Земли. Внутри белого карлика температура достигает 10 млн К и практически не меняется; только в тонкой оболочке из «обычного» вещества она резко падает до 10 000 К.
В 1996 г. были открыты космические тела, которые являются промежуточным звеном между звёздами и планетами. Они получили название «коричневые карлики», поскольку излучают слабо и только в инфракрасном диапазоне. Именно это излучение было обнаружено приборами, установленными на борту искусственных спутников. Коричневые карлики обладают слишком малой массой, что не обеспечивает температуры, необходимой для протекания термоядерной реакции превращения водорода в гелий. Гравитационное сжатие их массы достаточно лишь для того, чтобы достигнутая температура обеспечила в течение короткого (по космическим меркам) времени превращение дейтерия (тяжёлого изотопа водорода) в гелий. Масса коричневых карликов составляет всего лишь 0,01—0,07 массы Солнца. Про них можно сказать, что они ещё не звёзды, но уже не планеты.
Понять, как связаны между собой различные типы звёзд, как они возникают и как происходит их эволюция, оказалось возможным только на основе изучения всей совокупности звёзд, образующих огромные звёздные системы — галактики.

Вопросы 1. Чем объясняется изменение яркости некоторых двойных звёзд? 2. Во сколько раз отличаются размеры и плотности звёзд-сверхгигантов и карликов? 3. Каковы размеры самых маленьких звёзд?

Упражнение 19 1. Определите сумму масс двойной звезды Капелла, если большая полуось её орбиты равна 0,85 а. е., а период обращения 0,285 года. 2. Во сколько раз светимость Ригеля больше светимости Солнца, если его параллакс равен 0,003ʺ, а видимая звёздная величина 0,34? 3. Какова средняя плотность красного сверхгиганта, если его диаметр в 300 раз больше солнечного, а масса в 30 раз больше массы Солнца?
Иногда бывает непросто взвесить даже небольшие, земные, предметы. А как определяются массы звёзд или громадных галактик, если их невозможно поместить на весы? Да и где та точка опоры, с помощью которой Архимед советовал небесные тела кантовать? Исаак Ньютон принимал за массу тела количество имеющейся в нём материи. Но времена вносили корректировки в понимание проблемы, и теперь эту величину определяет инертность тел. Они тем тяжелее, чем труднее им предать ускорение. Масса тел определяется различными методами.
Именно определение земной массы стало первым этапом в решении задачи по вычислениям масс звёзд.
Применяя геодезические методы, была с большой точностью измерена линейная длина градуса дуги меридиана. Получив это значение и применив закон Всемирного тяготения, масса Земли была установлена. Она составила 6 . 1024 кг. Зная эту величину, использовав третий кеплеровский закон, узнали массу Луны – 7,3477·1022 кг. А это уже позволило определить массивность и самого нашего светила – 1,9891·1030 кг. После этого вычисление масс остальных объектов Солнечной системы не составило особого труда.
Методы измерений объектов в космосе
- Гравиметрический. Эта методика использует данные измерений силы тяжести, которая характеризует поверхность измеряемого тела. Имея значения силы тяжести и радиуса, например, Земли, можно вычислить её массу.
- Применяя третий, уточнённый, закон Кеплера. При наличии у планеты хотя бы одного спутника и известным: расстоянию до него и периоду обращения вокруг планеты, возможно определение соотношения масс планеты и звезды.
- Анализируя видимые возмущения одних небесных тел относительно движения других.
Определение массы звезды
Определение массивности звёзд с достаточной точностью не всегда возможно. Для этого должны совпасть два компонента: у звезды существует компаньон, и расстояние до неё известно. Сначала вычисляется общая сумма масс, а потом, в зависимости от некоторых компонентов, в частности, яркости, сумма делится пропорционально.
Имеющиеся вычисленные данные о ста двойных звёздах различных типов дали возможность увидеть важную закономерность: массы звёзд и их светимость находятся в прямой зависимости. А это позволяет оценить массивность звёзд по силе их светимости – звёздной величине.
То есть, чтобы рассчитать массу звезды, необходимо определить класс её светимости. Этот метод нельзя использовать лишь для белых карликов и пульсаров. Другой вариант измерения данного параметра основан на красных смещениях в поле тяготения звезды. Измеряются гравитационные смещения спектральных линий.
Измерение масс звёздных скоплений
Этот параметр определяются по общей сумме масс всех его компаньонов. В шаровых скоплениях не всё так просто: не всегда удаётся подсчитать участников скопления и определить их светимости. Поэтому применяются методы, имеющие под собой некоторые статистические принципы. Учитываются радиус скопления, а также отклонения лучевых скоростей конкретных звёзд от средних значений.
Масса галактики
Значение массы для галактики, например, нашей, определяется на базе фактического её вращения. Каждая звезда, в частности, Солнце, имеет центростремительное ускорение, определяемое притяжением галактического вещества в границах орбиты. Имея некоторые значения: расстояние от звезды до галактического ядра, её орбитальную скорость, можно вычислить и массу галактики.
Примеры
Звёзды разделяются по спектральному классу, звёздной величине, светимости. Но одной из основных их характеристик является, конечно же, масса. И тут нет прямой пропорции. Звёздный гигант, имея размер, в разы и сотни раз больший, чем Солнце, по массе может превосходить его не намного. Например, жёлтый гигант Капелла, главная звезда Возничего, больше Солнца по радиусу в 9 – 12 раз, а массивнее всего в 2,5 раза. А Бетельгейзе, красный сверхгигант Ориона, превышает солнечный радиус в 950 – 1200 раз, но массу имеет всего в 13 – 17 солнечных. А вот у белых карликов, обладающих массой, сравнимой с массой нашего светила, радиусы на два порядка меньше. Проще всего говорить о массах чёрных дыр. Они могут иметь минимальные значения – порядка 10-5 г (при радиусе около 10-35 м), но максимум их – бесконечность, к которой они устремлены.
Масса галактики – значение более солидное. Например, масса нашего Млечного Пути определена как 3 . 1012 масс Солнца, а таинственная галактика Андромеда массивнее нашей всего в полтора раза. Вероятно, самая большая из обнаруженных галактик – IC 1101. Она находится в созвездии Змеи, и до неё 1,07 млрд. световых лет. При невероятном диаметре в 6 млн. световых лет, масса её превышает солнечную в 24,5 триллиона раз! Если эту супергалактику поместить на место галактики нашей, то она успешно поглотит оба Магеллановых Облака, Андромеду и Треугольник.
Массы звёзд и галактик представить невероятно сложно. Для нас всё, что выходит за пределы в тысячи тонн, уже находится на грани восприятия. Но это понятно, ведь мы существуем в мире обычном, измеряемом единицами, которые можно «пощупать». Чтобы более зримо представлять макромиры, нужно в них погрузиться. Но и оказавшись там, вряд ли можно реально оценить массы звёзд и массы галактик.
Как учёные определяют массу планет и звёзд?
Гуру
(4626),
закрыт
13 лет назад
Корпускуляр
Гений
(68288)
13 лет назад
Массу планеты, имеющей спутник, очень легко рассчитать по характеристикам движения спутника. Хотя орбиты движения спутников эллиптические, но степень эллиптичности обычно очень мала и с хорошей точностью орбиту можно считать круговой. Для устойчивого движения всегда выполняется равенство гравитационной силы притяжения и центробежной силы: γmM/R² = mV²/R, где m – масса спутника, M – масса планеты, V – скорость движения спутника, R – расстояние от спутника до планеты. Сокращаем массу спутника m и получаем M = RV²/γ. Расстояние R легко измеряется с помощью телескопов: смотрят на спутник и саму планету из двух точек земной поверхности и видят их под разными углами, затем простейшими формулами геометрии высчитывают расстояние до спутника и планеты, а разность между этими расстояниями и дает искомую величину R. Зная удаление спутника от планеты и время его полного обращения, легко находят скорость V. И окончательно узнают массу планеты М. А затем вводят поправки на эллиптичность орбиты и корректируют найденную массу.
Определить массу планеты, не имеющей спутников (Венера и Меркурий) , заметно сложнее. Обычно это делается через гравитационные возмущения орбит. Чем ближе подходит Венера к Земле, тем сильнее притягивает её Земля и Венера как-бы немножко сходит со своей орбиты (Земля при этом также сходит) . Это изменение орбиты и называется гравитационным возмущением. Оно настолько мало, что даже в долгосрочной перспективе никак не скажется на судьбе планет. Но уже достаточно велико, чтобы быть обнаруженным в телескопы. Величина гравитационных возмущений орбит пропорциональна массам планет. Зная массу Земли, всегда можно подобрать такое значение массы Венеры, чтобы рассчитаннное возмущение орбиты совпало с тем, что наблюдается на практике. А затем точно таким же макаром ищут массу Меркурия.
Массу звезд ищут иным способом. Вначале находят массу Солнца по той же самой формуле, что я написал выше. Затем выбирают некоторую звезду и снимают максимально возможную информацию её излучения: светимость, спектр, распределение энергии по спектру, наличие линий поглощения и излучения в спектре, величину красного смещения и т. д. И все это сравнивают с теми же данными по Солнцу. Дело в том, что некоторые характеристики излучения звезды зависят от её массы. Сравнивая эти данные с данными Солнца и зная массу последнего, можно определить массу звезды.
Пользователь удален
Мыслитель
(6934)
13 лет назад
Это что же, выходит, Меркурий самая тяжелая планета в Солнечной системе (ответ на ответ колхозника) ? Дурдом. Масса планет рассчитывается по законам всемирного тяготения и законам небесной механики (обычно законам Кеплера) , связывающим массу и параметры эллиптических орбит. Расчет массы звезд – либо опять же по этим законам (например, для близких двойных звезд, для которых можно определить параметры орбит) , либо по их спектрам и светимости на основе законов звездной эволюции.