Как найти массу звезды зная светимость

Как найти массу звезды зная светимость

Зависимость масса — светимость — в астрофизике уравнение, показывающее связь между массой звезды и её светимостью. Данное уравнение имеет вид

{displaystyle {frac {L}{L_{odot }}}=left({frac {M}{M_{odot }}}right)^{a},}

где L⊙ и M⊙ — светимость и масса Солнца, 1 < a < 6.[1] Значение a = 3.5 обычно используется для звезд главной последовательности[2] с массами 2M⊙ < M < 20M⊙ и не применимо к красным гигантам или белым карликам. В случае достижения звездой
предела Эддингтона значение a = 1.

Для различных диапазонов масс звезд зависимость масса-светимость выглядит следующим образом:[1][3]

{displaystyle {frac {L}{L_{odot }}}approx 0.23left({frac {M}{M_{odot }}}right)^{2.3}qquad (M<0.43M_{odot })}
{displaystyle {frac {L}{L_{odot }}}=left({frac {M}{M_{odot }}}right)^{4}qquad qquad (0.43M_{odot }<M<2M_{odot })}
{displaystyle {frac {L}{L_{odot }}}approx 1.5left({frac {M}{M_{odot }}}right)^{3.5}qquad (2M_{odot }<M<20M_{odot })}
{displaystyle {frac {L}{L_{odot }}}approx 3200{frac {M}{M_{odot }}}qquad qquad (M>20M_{odot })}

Для звезд с массами меньше 0.43M⊙ основным механизмом переноса является конвекция, что значительно меняет соотношение. Для звезд с массами, превышающими 20M⊙, зависимость принимает вид L ∝ M.[1]
Можно показать, что данное изменение зависимости возникает благодаря увеличению давления излучения в массивных звездах. Данные уравнения получены эмпирически при определении масс звезд в двойных системах, расстояние до которых известно из измерений параллаксов или при применении других методов. При нанесении данных о достаточно большом количестве звезд на график с логарифмическим масштабом осей точки образуют линию, наклон которой показывает величину a.

Зависимость масса-светимость важна, поскольку позволяет оценить расстояние до двойных систем, которые слишком далеки для того, чтобы было возможным измерение их параллакса, в рамках метода динамических параллаксов. Также данная зависимость может быть использована для определения времени жизни звезды, поскольку оно приблизительно пропорционально отношению M/L.

Вывод уравнения[править | править код]

Вывод точного теоретического соотношения требует знания уравнения создания энергии и создания термодинамической модели внутренней части звезды. Однако основное соотношение L ∝ M3 можно вывести из основных законов физики при некоторых упрощающих предположениях.[4] Первый подобный вывод был создан астрофизиком Артуром Эддингтоном в 1924 г.[5] В рамках данного подхода вещество звезд представлялось моделью идеального газа. Далее будет представлен сходный алгоритм вывода зависимости, но не учитывающий оптическую непрозрачность.

В первом приближении звезды можно представить абсолютно черными телами с площадью поверхности 4πR2. По закону Стефана-Больцмана светимость равна

{displaystyle L=4pi R^{2}sigma T_{E}^{4},}

где σ — постоянная Стефана-Больцмана, равная 5,67 × 10−8Вт м−2 K−4.
При гидростатическом равновесии имеет место равенство

{displaystyle {frac {dP}{dr}}=-{frac {Gm(r)rho (r)}{r^{2}}}.}

При интегрировании данного равенства по r от 0 до R получается одно из выражений теоремы вириала:

{displaystyle langle Prangle =-{frac {1}{3}}{frac {E_{GR}}{V}}}.

Потенциальная энергия для сферически распределенной массы имеет вид

{displaystyle E_{GR}=-{frac {3}{5}}{frac {GM^{2}}{R}}.}

При подстановке данного выражения в предыдущую формулу и замене объема V на объем шара получаем приближенное равенство

{displaystyle langle Prangle approx {frac {GM^{2}}{4pi R^{4}}}}.

Одним из упрощений является предположение о справедливости уравнения состояния идеального газа для данной системы:

{displaystyle PV=nkT,qquad langle Prangle ={frac {langle rho rangle }{bar {m}}}kT.}

Выражение для температуры будет иметь вид

{displaystyle kT={frac {GM{bar {m}}}{3R}}}.

Здесь {displaystyle {bar {m}}} показывает среднюю массу частиц газа внутри звезды. При подстановке данного выражения в уравнение для светимости, а также при выражении радиуса в виде

{displaystyle R=left({frac {3}{4}}{frac {1}{rho pi }}Mright)^{frac {1}{3}}}

получим связь светимости и массы

{displaystyle Lvarpropto M^{3.33}}.

Несколько более точное выражение можно получить, приняв во внимание тот факт, что упоминавшееся уравнение позволяет получить среднюю температуру при известном среднем давлении, однако при выражении светимости необходимо знать температуру поверхности звезды. Поскольку звезды гораздо горячее в центральных областях, чем на поверхности, то следует оценить соотношение между поверхностной температурой и внутренней. Центральная часть звезды настолько горяча, что энергии требуется длительное время, чтобы покинуть центральную область; другими словами, термодинамическое равновесие достигается достаточно быстро. При помощи модели случайных блужданий можно оценить количество времени, требующееся для выхода энергии. В действительности, длина свободного пробега l фотонов для Солнца зависит от плотности и температуры, но в данном рассмотрении мы примем данную величину постоянной. После N взаимодействий, приводящих к N смещениям вектора движения в случайных направлениях, пройденное расстояние имеет вид

{displaystyle mathbf {D=l_{1}+l_{2}+cdots +l_{n}} }.

Квадрат модуля смещения можно выразить как

{displaystyle D^{2}=l_{1}^{2}+l_{2}^{2}+cdots +l_{n}^{2}+2(mathbf {l_{1}cdot l_{2}+l_{1}cdot l_{3}+cdots )} }.

При усреднении по большому количеству смещений слагаемые, содержащие скалярное произведение, обнулятся вследствие случайности направлений. Таким образом, при больших N имеет место выражение

{displaystyle D^{2}=l_{1}^{2}+l_{2}^{2}+cdots +l_{n}^{2}=Nl^{2}.}

Следовательно, для того, чтобы излучение покинуло Солнце, необходимо в среднем {displaystyle {frac {R^{2}}{l^{2}}}} переизлучений. Время, за которое данный процесс произойдет, составляет {displaystyle tapprox {frac {R^{2}}{cl}}}. Время, необходимое для прохождения радиуса Солнца без переизлучения, составляет {displaystyle {frac {R}{c}}}, что меньше предыдущего результата в {displaystyle {frac {l}{R}}} раз. Подставляя полученное соотношение в закон Стефана-Больцмана, получим выражение

{displaystyle T_{E}approx {Big [}{frac {l}{R}}{Big ]}^{frac {1}{4}}T_{I}}.

Итоговое выражение для светимости будет иметь вид[4]

{displaystyle Lapprox 4pi R^{2}sigma T_{I}^{4}{frac {l}{R}}approx {frac {(4pi )^{2}}{3^{5}}}{frac {sigma }{k^{4}}}G^{4}{bar {m}}^{4}langle rho rangle lM^{3}.}

Длина свободного пробега обратно пропорциональна произведению поперечного сечения и концентрации, следовательно

{displaystyle lvarpropto langle rho rangle ^{-1}.}

Подставляя данной выражение в предыдущую формулу, получим

{displaystyle Lvarpropto M^{3}.}

Различие между звездами малых и больших масс[править | править код]

Различие между случаями малых и больших звездных масс можно получить при выводе уравнений с учетом давления излучения. В данном случае проще рассматривать оптическую непрозрачность kappa и внутреннюю температуру {displaystyle T_{I}}. Более точно, следует рассмотреть среднюю температуру в зоне лучистого переноса.

Для градиента давления излучения справедливо равенство

{displaystyle {frac {dP_{rad}}{dr}}=-{frac {kappa rho }{c}}{frac {L}{4pi r^{2}}},}

где c — скорость света, {displaystyle 1/kappa rho =l} равно длине свободного пробега фотона.

Давление излучения связано с температурой соотношением {displaystyle P_{rad}={frac {4sigma }{3c}}{T_{I}}^{4},} следовательно,

{displaystyle {T_{I}}^{3}{frac {dT_{I}}{dr}}=-{frac {3kappa rho }{16sigma }}{frac {L}{4pi r^{2}}},}

откуда следует пропорциональность

{displaystyle Lvarpropto {T_{I}}^{4}{frac {R}{rho }}varpropto {T_{I}}^{4}{frac {R^{4}}{M}}.}

В зоне лучистого переноса гравитация уравновешивается давлением газа и излучения. Для звезд небольших масс давление излучения мало, следовательно, справедливо соотношение

{displaystyle T_{I}varpropto {frac {M}{R}}}.

Таким образом, выражение для светимости в данном случае имеет вид

{displaystyle Lvarpropto M^{3}.}

Для звезд больших масс давление излучения превосходит давление газа в зоне лучистого переноса. В таком случае справедливо выражение

{displaystyle {T_{I}}^{4}varpropto {frac {M^{2}}{R^{4}}},}

что приводит к виду соотношения массы и светимости:

{displaystyle Lvarpropto M.}

Примечания[править | править код]

  1. ↑ 1 2 3 Salaris, Maurizio; Santi Cassisi. Evolution of stars and stellar populations (англ.). — John Wiley & Sons, 2005. — P. 138—140. — ISBN 0-470-09220-3.
  2. ↑ Mass-luminosity relationship. Hyperphysics. Дата обращения: 23 августа 2009. Архивировано 22 октября 2019 года.
  3. ↑ Duric  (англ.) (рус., Nebojsa  (англ.) (рус.. Advanced astrophysics. — Cambridge University Press, 2004. — С. 19. — ISBN 978-0-521-52571-8.
  4. ↑ 1 2 Phillips, A.C. The Physics of Stars. — John Wiley & Sons, 1999. — ISBN 978-0-471-98798-7.
  5. ↑ Lecchini, Stefano. How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation (англ.). — Bern Studies in the History and Philosophy of Science. — ISBN 978-3-9522882-6-9. (недоступная ссылка)
Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,653
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,904
  • разное
    16,900

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Масса – это одно из самых важных свойств материи. Являясь мерой гравитационного взаимодействия, именно она во многом определяет облик нашей Вселенной – от звезд и планет до галактических скоплений. Однако, измерение этой величины в космических масштабах – совсем не простая задача. Так как же ученые узнают массы планет, звезд и других небесных тел?

Начнем с относительно простого – массы Земли. В качестве основы нам понадобится закон всемирного тяготения, сформулированный Исааком Ньютоном еще в 1666 году. Согласно ему, сила притяжения двух тел прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между объектами.

Как ученые определяют массы планет и звезд?

Из него легко можно вывести формулу для ускорения свободного падения. В свою очередь, находясь на Земле, эту величину можно измерить различными способами. Самый очевидный из них – сбросить с высокой башни тяжелый предмет и засечь время падения. Другой вариант – изготовить из нитки и грузика простейший маятник, после чего замерить период его колебаний. Если вам интересно попробовать провести этот несложный, но занимательный эксперимент самостоятельно – напишите об этом в комментариях, и мы обязательно посвятим ему одну из ближайших статей.

Как ученые определяют массы планет и звезд?

Радиус же нашей планеты также можно определить с довольно высокой точностью, не покидая ее – древние греки справлялись с этим еще три тысячи лет назад. Для этого потребуется две астролябии – так называется прибор для измерения высоты небесных тел на небосводе. Кроме того, необходим знакомый в другом городе, часы и любой способ связи. Нужно всего лишь одновременно измерить высоту солнца над горизонтом в полдень, после чего решить несложное уравнение.

Таким образом, зная радиус нашей планеты и ускорение свободного падения, можно рассчитать массу Земли. Разумеется, чем точнее будут измерены исходные данные, тем ближе к истине окажетсяконечный результат вычислений.

Прямым следствием из закона всемирного тяготения является третий закон Кеплера, связывающий орбиты и массы небесных тел. С его помощью можно узнать массу Луны, зная параметры ее орбиты и массу нашей планеты. Аналогично вычисляется масса Солнца, а от нее – всех остальных планет нашей системы.

С дальними же светилами все обстоит намного сложнее. Параметры двойных звезд относительно просто определяются по их взаимному движению, главное – правильно измерить расстояния. В случае же одиночных светил используются различные косвенные методы.

Например, на основе огромного количества наблюдений была сформулирована зависимость массы звезды от ее светимости. К сожалению, белые карлики и пульсары не подчиняются этой закономерности, и их параметры приходится определять иными методами.

Еще одним способом является спектральный анализ излучения звезды. Дело в том, что ее собственная гравитация искажает линии спектра подобно доплеровскому смещению. Массы экзопланет определяют по их влиянию на собственное движение материнского светила, а звездных скоплений – как сумму масс составляющих их объектов. Параметры же далеких галактик вычисляются либо по их вращению, либо по средней скорости собственного движения их компонентов.

Естественно, что чем дальше расположен объект от Земли, тем меньше точность, с которой можно вычислить его параметры. Например, масса нашей планеты определена с точностью 0,05%, Луны и Солнца – 0,1%, планет системы – до 0,7%. В то же время, погрешность измерения характеристик некоторых звезд может составлять от 20 до 70%, а галактик – еще больше. Как бы то ни было, эти данные постоянно уточняются, а новые технологии позволяют нам узнавать больше о нашей Вселенной.

#космос

#наука

#планета

#звезда

Больше новостей и самые свежие видео:

Наш Youtube

Наш Telegram

Источник

Иногда бывает непросто взвесить даже небольшие, земные, предметы. А как определяются массы звёзд или громадных галактик, если их невозможно поместить на весы? Да и где та точка опоры, с помощью которой Архимед советовал небесные тела кантовать? Исаак Ньютон принимал за массу тела количество имеющейся в нём материи. Но времена вносили корректировки в понимание проблемы, и теперь эту величину определяет инертность тел. Они тем тяжелее, чем труднее им предать ускорение. Масса тел определяется различными методами.

Именно определение земной массы стало первым этапом в решении задачи по вычислениям масс звёзд. 

Применяя геодезические методы, была с большой точностью измерена линейная длина градуса дуги меридиана. Получив это значение и применив закон Всемирного тяготения, масса Земли была установлена. Она составила 6 . 1024 кг. Зная эту величину, использовав третий кеплеровский закон, узнали массу Луны – 7,3477·1022 кг. А это уже позволило определить массивность и самого нашего светила – 1,9891·1030 кг. После этого вычисление масс остальных объектов Солнечной системы не составило особого труда.

Методы измерений объектов в космосе

  • Гравиметрический. Эта методика использует данные измерений силы тяжести, которая характеризует поверхность измеряемого тела. Имея значения силы тяжести и радиуса, например, Земли, можно вычислить её массу.
  • Применяя третий, уточнённый, закон Кеплера. При наличии у планеты хотя бы одного спутника и известным: расстоянию до него и периоду обращения вокруг планеты, возможно определение соотношения масс планеты и звезды.
  • Анализируя видимые возмущения одних небесных тел относительно движения других.

Определение массы звезды

Определение массивности звёзд с достаточной точностью не всегда возможно. Для этого должны совпасть два компонента: у звезды существует компаньон, и расстояние до неё известно. Сначала вычисляется общая сумма масс, а потом, в зависимости от некоторых компонентов, в частности, яркости, сумма делится пропорционально.

Имеющиеся вычисленные данные о ста двойных звёздах различных типов дали возможность увидеть важную закономерность: массы звёзд и их светимость находятся в прямой зависимости. А это позволяет оценить массивность звёзд по силе их светимости – звёздной величине.

То есть, чтобы рассчитать массу звезды, необходимо определить класс её светимости. Этот метод нельзя использовать лишь для белых карликов и пульсаров. Другой вариант измерения данного параметра основан на красных смещениях в поле тяготения звезды. Измеряются гравитационные смещения спектральных линий.

Измерение масс звёздных скоплений

Этот параметр определяются по общей сумме масс всех его компаньонов. В шаровых скоплениях не всё так просто: не всегда удаётся подсчитать участников скопления и определить их светимости. Поэтому применяются методы, имеющие под собой некоторые статистические принципы. Учитываются радиус скопления, а также отклонения лучевых скоростей конкретных звёзд от средних значений.

Масса галактики

Значение массы для галактики, например, нашей, определяется на базе фактического её вращения. Каждая звезда, в частности, Солнце, имеет центростремительное ускорение, определяемое притяжением галактического вещества в границах орбиты. Имея некоторые значения: расстояние от звезды до галактического ядра, её орбитальную скорость, можно вычислить и массу галактики. 

Примеры

Звёзды разделяются по спектральному классу, звёздной величине, светимости. Но одной из основных их характеристик является, конечно же, масса. И тут нет прямой пропорции. Звёздный гигант, имея размер, в разы и сотни раз больший, чем Солнце, по массе может превосходить его не намного.  Например, жёлтый гигант Капелла, главная звезда Возничего, больше Солнца по радиусу в 9 – 12 раз, а массивнее всего в 2,5 раза. А Бетельгейзе, красный сверхгигант Ориона, превышает солнечный радиус в 950 – 1200 раз, но массу имеет всего в 13 – 17 солнечных. А вот у белых карликов, обладающих массой, сравнимой с массой нашего светила, радиусы на два порядка меньше. Проще всего говорить о массах чёрных дыр. Они могут иметь минимальные значения – порядка 10-5 г (при радиусе около 10-35 м), но максимум их – бесконечность, к которой они устремлены.

Масса галактики – значение более солидное. Например, масса нашего Млечного Пути определена как 3 . 1012 масс Солнца, а таинственная галактика Андромеда массивнее нашей всего в полтора раза. Вероятно, самая большая из обнаруженных галактик – IC 1101. Она находится в созвездии Змеи, и до неё 1,07 млрд. световых лет. При невероятном диаметре в 6 млн. световых лет, масса её превышает солнечную в 24,5 триллиона раз! Если эту супергалактику поместить на место галактики нашей, то она успешно поглотит оба Магеллановых Облака, Андромеду и Треугольник.

Массы звёзд и галактик представить невероятно сложно. Для нас всё, что выходит за пределы в тысячи тонн, уже находится на грани восприятия. Но это понятно, ведь мы существуем в мире обычном, измеряемом единицами, которые можно «пощупать». Чтобы более зримо представлять макромиры, нужно в них погрузиться. Но и оказавшись там, вряд ли можно реально оценить массы звёзд и массы галактик.

Источник

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Планеты солнечной системы

Планеты солнечной системы

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Содержание:

  • 1 Рассчитываем массу Земли и Луны
  • 2 Общие методики определения масс планет
  • 3 Значения масс планет Солнечной системы
  • 4 Определение масс звезд и галактик

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Земля и луна

Земля и луна

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

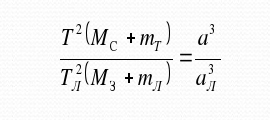
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Тела солнечной системы, расположенные по убыванию массыСамой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Источник

Добавить комментарий