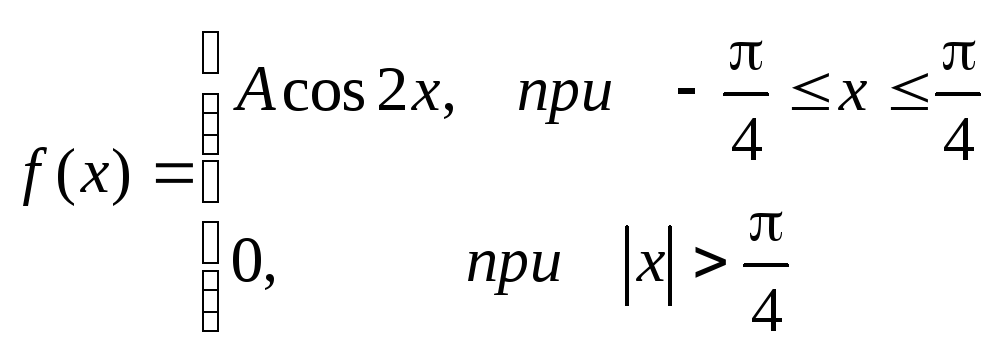Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Полезная страница? Сохрани или расскажи друзьям
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Понравилось? Добавьте в закладки
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение
- Закон распределения дискретной случайной величины
- Математическое ожидание
- Дисперсия
- Среднее квадратичное отклонение
- Правило трёх сигм
- Примеры
п.1. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют соответствие между полученными на опыте значениями этой величины X= {xi} и их вероятностями pi = P(xi).
При этом сумма всех вероятностей равна 1: (mathrm{sum_{i=1}^n p_i=1})
Закон распределения можно задать таблицей, графиком или аналитически (в виде формулы).
Например:
Закон распределения случайной величины X = {0;1;2;3}, равной числу выпадения орлов при 3 бросках монеты, аналитически задаётся формулой: $$ mathrm{ p_i=P(x_i)=P_3(i)=frac{C_3^{i}}{2^3}, i={0;1;2;3} } $$
В табличном виде:
|
xi |
pi |
|
0 |
1/8 |
|
1 |
3/8 |
|
2 |
3/8 |
|
3 |
1/8 |
В виде графика:
п.2. Математическое ожидание
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ mathrm{ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} } $$ Математическое ожидание является средним значением величины X.
Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
M(C) = C
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
M(X + Y) = M(X) + M(Y)
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
M(XY) = M(X) · M(Y)
6) Постоянный множитель можно вынести за знак математического ожидания:
M(CX) = C · M(X)
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):
| Число белых шаров, xi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | (mathrm{C_5^0q^5}) | (mathrm{C_5^1pq^4}) | (mathrm{C_5^2p^2q^3}) | (mathrm{C_5^3p^3q^2}) | (mathrm{C_5^4p^4q}) | (mathrm{C_5^5p^5}) |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Найдём математическое ожидание для данного распределения:
M(X) = 0 · 0,0074 + 1 · 0,0618 + … + 5 · 0,0954 = 3,125
п.3. Дисперсия
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ mathrm{ D(X)=M(X-M(X))^2 } $$ На практике дисперсия рассчитывается по формуле: $$ mathrm{ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) } $$
Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
D(C) = 0
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
D(X + Y) = D(X) + D(Y)
5) Постоянный множитель можно вынести за знак дисперсии:
D(CX) = C2 · D(X)
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
pi
0,0074
0,0618
0,2060
0,3433
0,2861
0,0954
1
xip1
0
0,0618
0,4120
1,0300
1,1444
0,4768
3,125
(mathrm{x_i^2})
0
1
4
9
16
25
–
(mathrm{x_i^2p_i})
0
0,0618
0,8240
3,0899
4,5776
2,3842
10,9375
Получаем: D(X) = 10,9375 – 3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ mathrm{ sigma(X)=sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
σ(C) = 0
4) Постоянный множитель можно вынести за знак СКО:
σ(CX) = C · σ(X)
п.5. Правило трёх сигм
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и (mathrm{sigma(X)=sqrt{npq}}).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
pi
1/6
1/6
1/6
1/6
1/6
1/6
1
xip1
1/6
1/3
1/2
2/3
5/6
1
3,5
(mathrm{x_i^2})
1
4
9
16
25
36
–
(mathrm{x_i^2p_i})
(mathrm{frac16})
(mathrm{frac23})
(mathrm{1frac12})
(mathrm{2frac23})
(mathrm{4frac16})
6
(mathrm{15frac16})
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=1}^6 x_ip_i=3,5 }\ mathrm{ D(X)=sum_{i=1}^6 x_i^2p_i-M^2(X)=15frac16-3,5^3=2frac{11}{12} }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{2frac{11}{12}}approx 1,7 } end{gather*} Ответ: (mathrm{M(X)=3,5; D(X)=2frac{11}{12}; sigma(X)approx 1,7}).
Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.
Используем свойства мат.ожиданий и дисперсий.
Пусть X – очки на первом кубике, Y – на втором.
Параметры распределения для каждого из кубиков рассчитаны в примере 1.
(mathrm{M(X)=M(Y)=3,5, D(X)=D(Y)=2frac{11}{12}}).
Для суммы очков получаем:
(mathrm{M(X+Y)=M(X)+M(Y)=3,5+3,5=7})
(mathrm{D(X+Y)=D(X)+D(Y)=2frac{11}{12}+2frac{11}{12}=5frac56})
(mathrm{sigma(X+Y)=sqrt{D(X+Y)}=sqrt{5frac56}approx 2,4})
Ответ: (mathrm{M(X+Y)=7; D(X+Y)=5frac56; sigma(X+Y)approx 2,4}).
Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.
Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:
(mathrm{x_i^2p_i})
0
p
p
Мат.ожидание первого опыта (mathrm{M(X)=sum x_ip_i=p}).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (mathrm{X=X_1+X_2+…+X_n}). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: begin{gather*} mathrm{ M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)= }\ mathrm{=underbrace{p+p+…+p}_{n text{раз}}=np } end{gather*} Дисперсия первого опыта (mathrm{D(X)=sum x_i^2p_i-M(X)=p-p^2=p(1-p)=pq})
По свойству дисперсии суммы независимых событий: begin{gather*} mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\ mathrm{=underbrace{pq+pq+…+pq}_{n text{раз}}=npq } end{gather*} Что и требовалось доказать.
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. begin{gather*} mathrm{ M(X)=np=100cdot 0,4=40 }\ mathrm{D(X)=npq=100cdot 0,4cdot 0,6=24 }\ mathrm{sigma(X)=sqrt{D(X)}=sqrt{24}approx 4,9} end{gather*} Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X)lt Xlt M(X)+3sigma(X) }\ mathrm{40-3cdot 4,9lt Xlt 40+3cdot 4,9 }\ mathrm{25,3lt Xlt 54,7}\ mathrm{26leq Xleq 54} end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: (mathrm{M(X)=40; D(X)=24; sigma(X)approx 4,9; 26leq Xleq 54})
Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?
По условию: (mathrm{n=10, p=frac14, q=frac34}).
Для каждого ответа может быть два исхода: «угадал»/ «не угадал».
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. $$ mathrm{ P_{10}(k)=C_{10}^kp^kq^{10-k}=C_{10}^kfrac{3^{10-k}}{4^{10}}=left(frac34right)^{10}frac{C_{10}^k}{3^k} } $$ Строим расчётную таблицу. Для (mathrm{C_{10}^k}) используем рекуррентную формулу (см. §36 данного справочника): $$ mathrm{ C_{n}^k=frac{n-k+1}{k}C_n^{k-1} } $$
| (mathrm{x_i=k}) | (mathrm{C_k}) | (mathrm{3^k}) | (mathrm{p_i(x_i)}) | (mathrm{x_icdot p_i}) | (mathrm{x_i^2}) | (mathrm{x_i^2cdot p_i}) |
| 0 | 1 | 1 | 0,0563135 | 0,0000000 | 0 | 0,0000000 |
| 1 | 10 | 3 | 0,1877117 | 0,1877117 | 1 | 0,1877117 |
| 2 | 45 | 9 | 0,2815676 | 0,5631351 | 4 | 1,1262703 |
| 3 | 120 | 27 | 0,2502823 | 0,7508469 | 9 | 2,2525406 |
| 4 | 210 | 81 | 0,1459980 | 0,5839920 | 16 | 2,3359680 |
| 5 | 252 | 243 | 0,0583992 | 0,2919960 | 25 | 1,4599800 |
| 6 | 210 | 729 | 0,0162220 | 0,0973320 | 36 | 0,5839920 |
| 7 | 120 | 2187 | 0,0030899 | 0,0216293 | 49 | 0,1514053 |
| 8 | 45 | 6561 | 0,0003862 | 0,0030899 | 64 | 0,0247192 |
| 9 | 10 | 19683 | 0,0000286 | 0,0002575 | 81 | 0,0023174 |
| 10 | 1 | 59049 | 0,0000010 | 0,0000095 | 100 | 0,0000954 |
| Σ | 1 | 2,5 | 8,125 |
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=0}^{10} x_ip_i=2,5 }\ mathrm{ D(X)=sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{1,875}approx 1,37 } end{gather*}
Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X) lt Xlt M(X)+3sigma(X) }\ mathrm{ 2,5-3cdot 1,37lt X lt 2,5+3cdot 1,37 }\ mathrm{ -1,61lt Xlt 6,61 }\ mathrm{ 0leq Xleq 6 } end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.
Вероятность угадать хотя бы один ответ: begin{gather*} mathrm{ P(Xgeq 1)=1-p_0approx 1-0,0563=0,9437 }end{gather*} Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: begin{gather*} mathrm{ P(Xgeq 5)=1-left(sum_{i=0}^{4}{p_i} right)approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.
Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
.
Принимая во внимание свойства
математического ожидания, легко показать
что
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
.
=9
=2,31.
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:
Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до.
Решение:
Для нахождения коэффициента авоспользуемся свойством.
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал.
Решение:
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке
:
2) На участке
3) На участке
Итого:
Найдем вероятность попадания случайной
величины в интервал
.
Ту же самую вероятность можно искать
и другим способом:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
22
Апр 2019
Теория вероятностей
Математическое ожидание
Математическое ожидание.
В этой статье мы рассмотрим определение и свойства математического ожидания, а также рассмотрим примеры решения задач.
Рассмотрим некоторую случайную величину , которая может принимать числовые значения
Пусть распределение вероятностей случайной величины задано таблицей:
Математическим ожиданием случайной величины называют число
Математическое ожидание называют также ожидаемым значением случайной величины
, средним значением случайной величины
.
Свойства математического ожидания.
Свойство 1. Пусть – случайная величина,
– некоторое число. Рассмотрим случайную величину
. Тогда
Свойство 2. Пусть и
– две случайные величины. Тогда
– тоже случайная величина, и при этом:
Это значит, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
Свойство 3. Если случайная величина принимает значения
с одинаковой вероятностью, то
Это значит, что если все значения случайной величины равновероятны, то математическое ожидание
равно среднему арифметическому числовых значений случайной величины
.
Пример 1. Страховой полис КАСКО в страховой компании стоит 35 000 рублей. По статистике в течение года владелец автомобиля попадает в мелкую аварию с вероятностью 0,18, и средняя сумма страховой выплаты при этом равна 50 000 рублей. С вероятностью 0,034 автомобилист попадает в серьезную аварию, и средняя сумма выплаты при этом 700 000 рублей. Найдите
- Математическое ожидание случайной величины “средняя сумма страховой выплаты”
- Математическое ожидание случайной величины “средний доход страховой компании от продажи одного полиса”
Решение. показать
Пример 2. Случайная величина задана распределением:
- Сколько значений принимает случайная величина
?
- Найдите математическое ожидание случайной величины
.
Решение. показать
Пример 3. В торговом центре установлены два автомата, продающие кофе. С вероятностью к вечеру в первом автомате заканчивается кофе. Во втором автомате кофе заканчивается к вечеру с вероятностью
. Найдите математическое ожидание числа автоматов, в которых к вечеру закончится кофе.
Решение. показать
Пример 4. Баскетболист попадает в корзину с вероятностью . Найдите математическое ожидание числа попаданий при 50 бросках.
Решение. показать
Пример 5. Василий пытается отправить СМС в условиях слабой мобильной связи. Телефон делает попытки отправить СМС до тех пор, пока это не удастся. Известно, что вероятность удачной попытки равна независимо от предыдущих попыток. Найдите математическое ожидание числа сделанных попыток.
Решение. показать
Пример 6. Найдите математическое ожидание случайной величины “число неудач” в серии из 16 испытаний Бернулли с вероятностью успеха
в одном испытании.
Решение. показать
Пример 7. Найдите математическое ожидание случайной величины “число очков, выпавших на игральной кости”.
Решение. показать
Пример 8. Игральную кость бросают 5 раз. Найдите математическое ожидание суммы выпавших очков.
Решение. показать
Репетитор по математике И.В. Фельдман

Математическое ожидание
Данный калькулятор предназначен для вычисления математического ожидания дискретной случайной величины онлайн.
Оценка математического ожидания и дисперсии случайной величины имеет большое значение в теории вероятности.
Математическое ожидание – среднее значение случайной величины. Чтобы найти математическое ожидание случайной величины, следует вычислить сумму парных произведений всех возможных значений случайной величины на соответствующие им вероятности.
Свойства математического ожидания заключаются в следующем. Во-первых, математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий. Во-вторых, математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
Как найти среднее значение , формула (на примере следующих величин):
xi= 1 ; 2 ; 5 ; 6 (случайные величины)
pi = 0.1 ; 0.3 ; 0.1 ; 0.5 (вероятность)
M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 1×0.1 + 2×0.3 + 5×0.1 + 6×0.5 = 0.1 + 0.6 + 0.5 + 3 = 4.2
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»