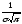Равномерное случайное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Равномерным называют распределение вероятностей непрерывной случайной величины
, если на интервале
, которому принадлежат все возможные
значения
, плотность сохраняет постоянное значение.
Функция распределения
равномерного закона:
Числовые характеристики равномерного распределения
Математическое ожидание равномерно распределенной случайной величины:
Дисперсия
равномерного случайного
распределения:
Среднее квадратическое отклонение случайной величины, распределенной равномерно:
Для равномерного распределения коэффициент асимметрии:
Коэффициент эксцесса
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Кроме равномерного, основные законы распределения непрерывных случайных величин:
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Экспоненциальный (показательный) закон распределения случайной величины
Примеры решения задач
Пример 1
Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность вероятности
равномерного распределения на интервале
:
Искомая вероятность:
Ответ:
.
Пример 2
Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).
Решение
Плотность
вероятности случайной величины, распределенной равномерно на интервале
В нашем
случае
Получаем:
Функцию
распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
Построим
графики:
График плотности распределения
График функции распределения
Математическое
ожидание величины, распределенной равномерно:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
равномерного распределения:
Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:
Ответ:
Пример 4
Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.
Решение
Дисперсия
равномерного распределения:
при
начале интервала
:
Искомый
интервал времени:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Случайные
величины X2, X3, X4 имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<Xi<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.
Задача 2
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, xmod, xmed, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.
Задача 3
Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].
Найти:
1) дифференциальную и интегральную
функцию распределения, а также построить их графики.
2) математическое ожидание и
дисперсию;
2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).
Задача 5
Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.
Задача 6
Равномерно распределенная случайная
величина
задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).
Задача 7
Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x0.2.
Задача 8
Случайная
величина
равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).
Задача 9
Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].
Задача 10
Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?
Задача 11
Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].
Задача 12
Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.
Задача 13
СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.
Задача 15
Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.
Задача 16
Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].
Задача 17
Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).
Задача 18
По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.
Задача 19
Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.
Задача 20
Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 октября 2020 года; проверки требуют 5 правок.
| Непрерывное равномерное распределение | |
|---|---|
 Плотность вероятности Плотность вероятности |
|
 Функция распределения Функция распределения |
|
| Обозначение |
 |
| Параметры |
 , ,  — коэффициент сдвига, — коэффициент сдвига,  — коэффициент масштаба — коэффициент масштаба |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
любое число из отрезка ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Непреры́вное равноме́рное распределе́ние в теории вероятностей — распределение случайной вещественной величины, принимающей значения, принадлежащие некоторому промежутку конечной длины, характеризующееся тем, что плотность вероятности на этом промежутке почти всюду постоянна.
Определение[править | править код]
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


Пишут: ![Xsim U[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d509fb56e608a786132dbf75361145b770d13b)




Функция распределения[править | править код]
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
.
Производящая функция моментов[править | править код]
Простым интегрированием получаем производящую функцию моментов:
,
откуда находим все интересующие моменты непрерывного равномерного распределения:
,
,
.
Вообще,
.
Стандартное равномерное распределение[править | править код]
Если 

![Xsim U[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3610abb42eb437d4b299a01c755ba35989970ea)
Имеет место элементарное утверждение:
- Если случайная величина
и
, то
.
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Существуют также частные преобразования, позволяющие на основе равномерного распределения получить случайные распределения другого вида. Так, например, для получения нормального распределения служит преобразование Бокса — Мюллера.
См. также[править | править код]
- Дискретное равномерное распределение;
- Метод обратного преобразования.
Равномерно распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ – распределенных по равномерному закону.
В сущности, равномерное распределение – самое простое из семейства непрерывных, и определяется тем, что плотность распределения постоянна (равна константе) на всем интервале: $f(x)=c=frac{1}{b-a}, xin (a;b)$ (а вне его равна нулю):
$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$
Функция распределения для нее вычисляется практически в уме:
$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$
Для равномерного на интервале $(a;b)$ распределения известны формулы для числовых характеристик. Математическое ожидание $M(X)=frac{a+b}{2}$, дисперсия $D(X)=frac{(b-a)^2}{12}$, среднее квадратическое отклонение $sigma(X)=frac{b-a}{2sqrt{3}}$.
В жизни равномерным распределением часто моделируют время ожидания транспорта, ошибки округления в пределах цены деления.
В этом разделе мы приведем разные примеры задач с полным решением, где используются равномерно распределенные случайные величины.
Спасибо за ваши закладки и рекомендации
Примеры решений
Задача 1. Автобусы идут с интервалом 5 минут. Полагая, что случайная величина $xi$ – время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания и среднеквадратическое уклонение времени ожидания.
Задача 2. Телефонный звонок должен последовать от 10 ч до 10 ч 20 мин. Какова вероятность того, что звонок произойдет в последние 10 мин указанного промежутка, если момент звонка случаен?
Задача 3. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
Задача 4. В здании областной администрации случайное время ожидания лифта равномерно распределено в диапазоне от 0 до 3 минут. Найти а) плотность распределения времени ожидания, б) вероятность ожидания лифта более чем 2 минуты, в) вероятность того, что лифт прибудет в течение первых 15 секунд, г) среднее время ожидания лифта и дисперсию времени ожидания.
Задача 5. Случайная величина $X$ задана интегральной $F(x)$ или дифференциальной $f(x)$ функцией. Требуется:
а) найти параметр $C$;
б) при заданной интегральной функции найти дифференциальную функцию; а при заданной дифференциальной функции найти интегральную функцию;
в) построить графики функций $F(x)$ и $f(x)$;
г) найти математическое ожидание $M[X]$ дисперсию $D[X]$ среднее квадратическое отклонение $sigma[X]$;
д) вычислить вероятность попадания в интервал $P(alt X lt b)$;
е) определить, квантилем какого порядка является точка $x_p$;
ж) вычислить квантиль порядка $p$.
$$
f(x)=
left{
begin{array}{l}
{0,x lt -1,} \
{C, -1 le x le 1} \
{0, xgt 1.}
end{array}
right.
$$
Задача 6. Дана плотность распределения $p(x)$ случайной величины $xi$. Найти параметр $gamma$, математическое ожидание $Mxi$, дисперсию $Dxi$, функцию распределения случайной величины $xi$, вероятность выполнения неравенства $x_1 lt xi lt x_2$.
$$a=1, b=1,8, x_1=1,3, x_2=1,6.$$
$$
p(x)=
left{
begin{array}{l}
{1,x in [gamma; 1,8],} \
{0,x notin [gamma; 1,8].} \
end{array}
right.
$$
Задача 7. Случайная величина Х равномерно распределена в интервале (1;8). Найти:
а) дифференциальную функцию,
б) интегральную функцию,
в) математическое ожидание, дисперсию и среднее квадратическое отклонение,
г) вероятность попадания в интервал (3;5).
Задача 8. Функция распределения непрерывной случайной величины задана следующим образом:
$$
F(x)=
left{
begin{array}{l}
{0,x lt a,} \
{frac{x-1}{2}, x in [a,b]} \
{1, xgt b.}
end{array}
right.
$$
Определить параметры $а$ и $b$, найти плотность вероятности, числовые характеристики и вероятность попадания случайной величины в интервал $[-1, 2]$. Построить графики $р(x)$ и $F(x)$.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Равномерное
распределение
Определение.
Будем говорить, что распределение
вероятностей непрерывной случайной
величины является равномерным
распределением, если плотность вероятности
случайной величины Х имеет вид:
f(x)=
Найдем
значение с.
Так
как плотность вероятности удовлетворяет
условию:
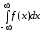
то
получаем:
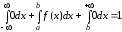
Так
как f(x)=c
на промежутке [a;b],
то
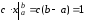
следовательно,c
=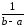
Итак,
равномерно распределённая случайная
величина имеет плотность вероятности:
f(x)=
Пример. Если
распределение случайной величины Х –
равномерное и задан отрезок [2;8], то b–a= 8 – 2 = 6 и
f(x)=
Найдем числовые характеристики
равномерного распределения.
-
Математическое
ожидание равномерного распределения.
М(Х)=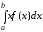
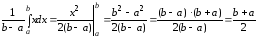
Пример.
Для предыдущей задачи найдем математическое
ожидание
М(Х)=
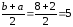
-
Дисперсия
равномерного распределения.
D(Х)
=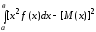
=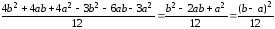
Пример. Для предыдущей задачи найдем
дисперсию:
D(Х)
=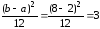
Нормальное
распределение
Определение.
Случайная величина Х имеет нормальный
закон распределения, если ее функция
плотности вероятности имеет вид:
f(x)=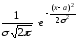
где
σ и a–
параметры распределения.
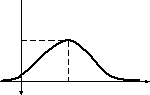
Определение.
График функции f(x)
называется нормальной
кривой или
кривой нормального распределения.
Методами
дифференциального исчисления можно
установить, что:
-
кривая
симметрична относительно прямой х=a; -
функция
имеет максимум при х=a
f(a)=
;
-
по
мере удаления х от точки a
функция убывает и при х→∞
кривая приближается к оси Ох; -
кривая
выпукла вверх при х є (a– σ; a
+ σ) и
выпукла
вниз при х є (–∞;
a
– σ) и х є
(a
+ σ; + ∞).
f(x)
0
a
X
Рис.
4. Кривая нормального распределения.
Замечание.
Форма кривой изменяется с изменением
параметра σ. С возрастанием σ кривая
f(x)
становится более пологой и растянутой
вдоль оси Ох.
Значениям случайной величины, близким
к математическому ожиданию, соответствует
большая плотность вероятности, то есть
малые отклонения значений случайной
величины от ее математического ожидания
встречаются чаще, чем большие.
Так как случайная величина определена
на всей числовой оси, то при вычислении
числовых характеристик рассматривается
интеграл на промежутке (– ∞; +∞). Можно
показать, что:
М(Х)
=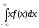
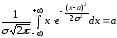
D(Х)=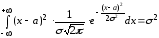
σ(Х)
= σ.
Свойства
нормального распределения.
-
Вероятность
того, что нормально распределенная
случайная величина Х примет значение,
принадлежащее интервалу (α;
β), находится по формуле:
Р(α
< Х < β) = Ф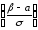
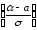
где
Φ(х)
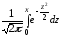
-
Вероятность
того, что абсолютная величина отклонения
меньше положительного числа δ находится
по формуле:
Р(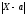
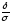
В
частности при a=0
справедливо равенство:
Р(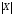
2Ф(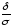
Правило
«3 σ».
Для
нормально распределенной случайной
величины велика вероятность того, что
при однократном испытании отклонение
величины от ее математического ожидания
не превышает среднего квадратического
отклонения.
Преобразуем
формулу Р(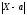
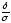
положив δ=σ·t. В итоге получим
Р(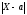
Если
t=3
и, следовательно, σ·t=3σ, то
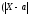
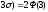
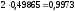
то есть вероятность того, что отклонение
от математического ожидания по абсолютной
величине будет меньше утроенного
среднего квадратического отклонения,
равна 0,9973. Это и есть правило «3 σ».
Другими
словами, вероятность того, что абсолютная
величина отклонения превысит утроенное
среднее квадратическое отклонение,
очень мала, а именно равна 0,0027.
Это
означает, что лишь в 0,27% случаев так
может произойти, что значения нормально
распределенной случайной величины
выйдут за пределы интервала (a
– 3σ; a
+ 3σ). Такие события, исходя из принципа
невозможности маловероятных событий,
можно считать практически невозможным.
В этом и состоит сущность правила трех
сигм.
Пример
1. Математическое
ожидание и среднее квадратическое
отклонение нормально распределенной
случайной величины Х равны соответственно
11 и 4. Найти вероятность того, что в
результате испытания Х примет значение,
заключенного в интервале (19;23).
Решение. Воспользуемся формулой:
Р(α<Х<β)=Ф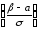
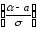
По
условию, α = 19; β = 23; а = 11; σ = 4, тогда
Р(19<Х<23)=Ф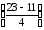
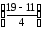
Ф(3)–Ф(2).
По
таблице приложения 2 находим: Ф(3)=0,49865,
Ф(2)=0,4772.
Найдем
искомую вероятность (вероятность того,
что в результате испытания Х примет
значение, заключенное в интервале
(19;23)):
Р(19<Х<23)=0,49865
–0,4772=0,02145.
Пример 2. Математическое ожидание
нормально распределенной случайной
величины Х равно 5 и среднее квадратическое
отклонение равно 2. Написать плотность
вероятности Х.
Решение. Плотность нормально распределенрон
случайной величины Х имеет вид:
f(x)=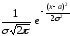
Подставив
a=5
и σ=2, получим:
f(x)=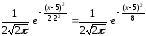
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
![{displaystyle f_{X}(x)=left{{begin{matrix}{dfrac {1}{b-a}},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa8944569e39923b3f52c67f007c6a5dcac00350)



![{mathbb {E}}left[Xright]={frac {a+b}{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3529daac6c04d15e40b6dc193b3b14d67f01ad)
![{mathbb {E}}left[X^{2}right]={frac {a^{2}+ab+b^{2}}{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94a9118d445bc34cfb654224f1e06635edfdda79)
![{displaystyle operatorname {D} left[Xright]={frac {(b-a)^{2}}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f29de127da904f44ea2822eb5cc918d0ebfef45d)
![{mathbb {E}}left[X^{n}right]={frac {1}{n+1}}sum limits _{{k=0}}^{n}{a^{k}b^{{n-k}}}={frac {b^{{n+1}}-a^{{n+1}}}{(b-a)(n+1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72d1e3efc704c61230bde3c4024bed54b6ee813c)

![{displaystyle Ysim U[min(a,b),max(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f98e26ac20e4c3e9884f9bc25c641b056a0e7d97)
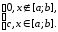
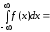
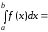
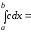
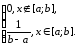
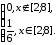
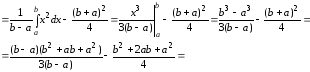
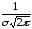 ;
; ∞
∞