Как найти математическое ожидание интегральной функции

Для непрерывной
случайной величины в отличие от дискретной
нельзя построить таблицу распределения.
Поэтому непрерывные случайные величины
изучают другим способом.

Пусть X
– непрерывная случайная величина с
возможными значениями из некоторого
интервала (a;
b)
и x
– действительное число. Под выражением
X
< x
понимается
событие «случайная величина X
приняла значение, меньшее x».
Вероятность этого события P(X
< x)
есть некоторая функция переменной x.

Определение.
Интегральной
функцией распределения
непрерывной случайной величины X
называется функция
,
равная вероятности того, что X
приняла значение, меньшее x:

(1)

Функция распределения
совершенно также определяется для
дискретных случайных величин.

Свойства
интегральной функцией распределения
.

1. 
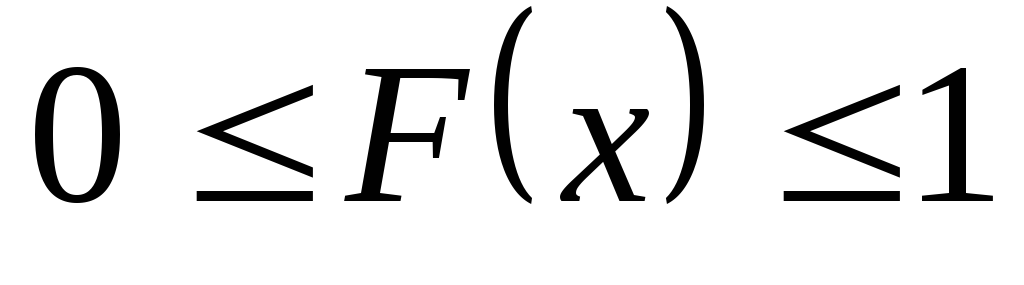
   (эта функция есть
   вероятность).

2. 
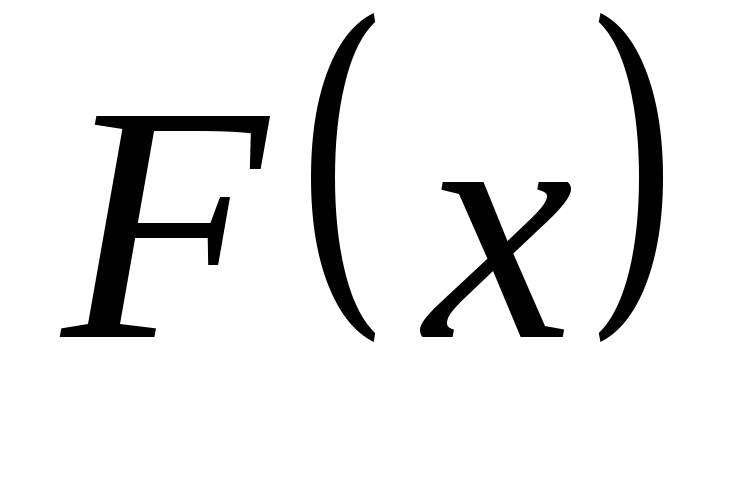
   – неубывающая
   функция.

3. Вероятность
   попадания случайной величины X
   в полуинтервал
   
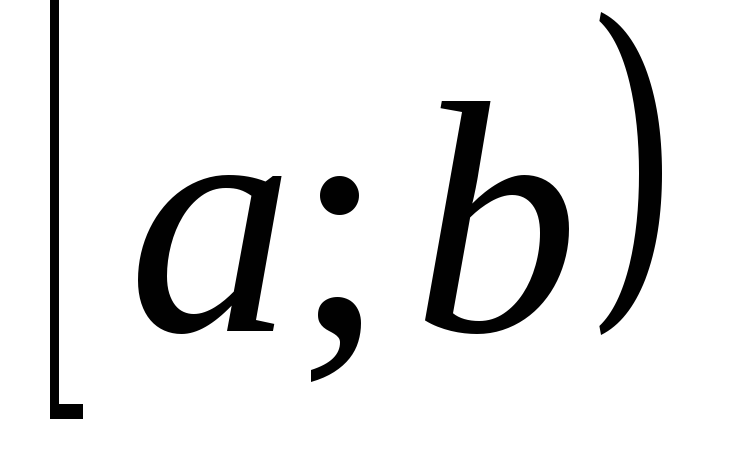
   равна разности между значениями функции
   распределения в правом и левом концах
   интервала (a;
   b):

1. Вероятность того,
   что непрерывная случайная величина X
   примет какое-либо заранее заданное
   значение, равна нулю:

1. Вероятности
   попадания непрерывной случайной
   величины в интервал, сегмент и полуинтервал
   с одними и теми же концами одинаковы:

1. Если возможные
   значения случайной величины X
   принадлежат интервалу (a;
   b),
   то

   1. 
      при
      ,

   2. 
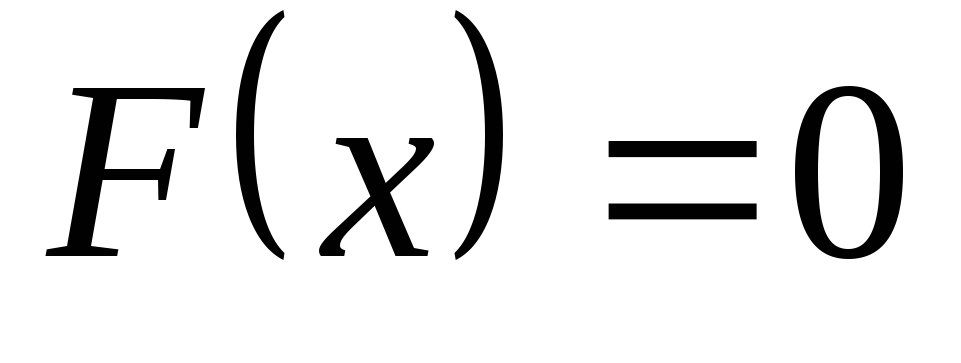
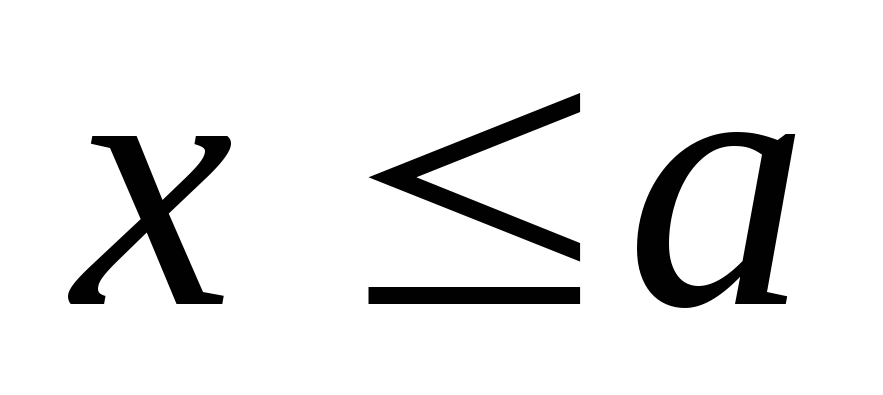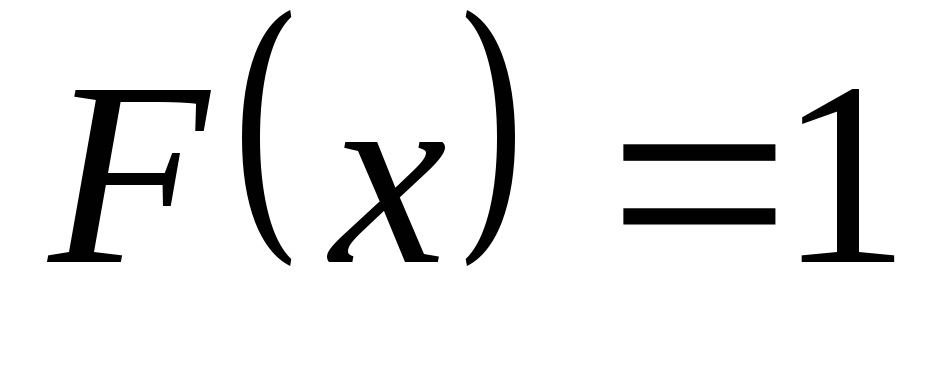
      при
      .

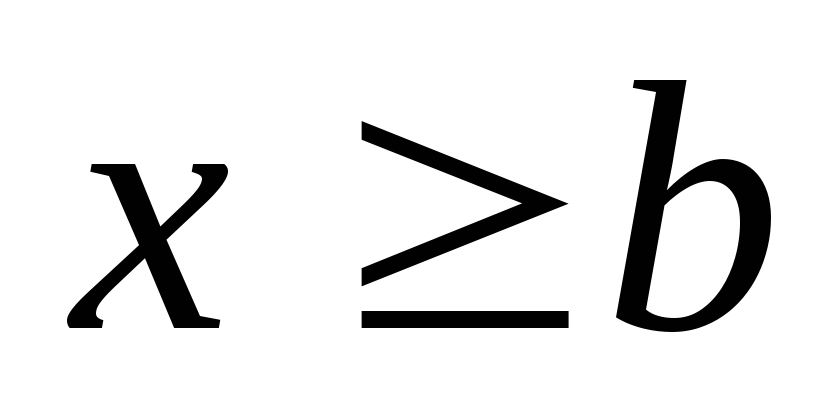Следствие.
,
.

Определение.
Дифференциальной
функцией распределения
непрерывной случайной величины X
называется функция
,
равная производной интегральной функции:

(2)

Так как

– неубывающая функция, то
.

Теорема.
Вероятность попадания непрерывной
случайной величины X
в интервале (a;
b)
равна определенному интегралу от
дифференциальной функции распределения
величины X,
взятому в пределах от a
до b:

(3)

Из (3) следует, что
геометрически вероятность

представляет собой площадь криволинейной
трапеции, ограниченной графиком плотности
вероятности

и отрезками прямых y
= 0, x = a,
x = b.

Следствие.
В частности, если

– четная функция и концы интервала
симметричны относительно начала
координат, то

На основании
формулы Ньютона-Лейбница можно записать
,
откуда, в силу следствия 1, можно записать:
(4).

Верно также
равенство:
(5).

Пример.
Задана плотность вероятности случайной
величины X

.

Требуется найти
коэффициент A,
функцию распределения F(x)
и вероятность попадания случайной
величины X
в интервал (0; 1).

Коэффициент A
найдем, воспользовавшись соотношением
(5).

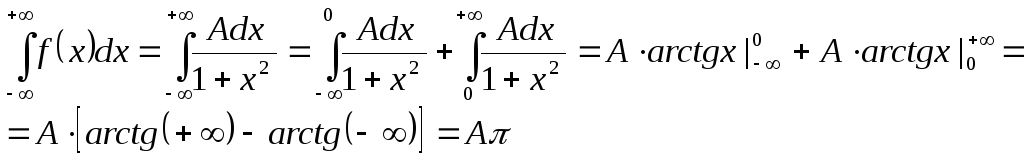
Так как
,
откуда
.

Применяя формулу
(4), получаем функцию распределения
.

Наконец, на основании
3 и 5 свойств, с учетом найденной функции
F(x)
получим

.

38. Математическое ожидание и дисперсия непрерывной случайной величины.

Определение.
Математическим
ожиданием непрерывной случайной величины
X
с плотностью
вероятности

называют величину несобственного
интеграла (если он сходится):

(1)

Свойства
математического ожидания непрерывной
случайной величины.

1. Математическое
   ожидание постоянной величины C
   равно этой величине.

2. Постоянный
   множитель можно выносить за знак
   математического ожидания, т.е.
   .

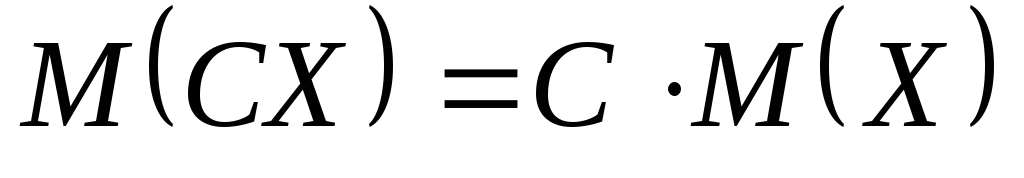3. Математическое
   ожидание суммы двух случайных величин
   X
   и Y
   равно сумме их математических ожиданий:
   M(X+Y)
   = M(X)
   + M(Y).

4. Математическое
   ожидание произведения двух независимых
   случайных величин равно произведению
   их математических ожиданий: M(XY)
   = M(X)
   M(Y).

5. Математическое
   ожидание разности – двух случайных
   величин X
   и Y
   равно разности их математических
   ожиданий: M(X–Y)
   = M(X)
   – M(Y).

Определение.
Дисперсией
непрерывной случайной величины X,
математическим ожиданием которой

и функция

является ее плотностью вероятности,
называется величина несобственного
интеграла (если он сходится):

(2)

Математическое
ожидание и дисперсия непрерывной
случайной величины имеют те же свойства,
что и математическое ожидание и дисперсия
дискретной случайной величины.

Для непрерывной
случайной величины X
среднее квадратическое отклонение

определяется, как и для дискретной
величины, формулой
.

Свойства дисперсии
дискретной случайной величины.

1. Дисперсия дискретной
   случайной величины X
   равна разности между математическим
   ожиданием квадрата величины X
   и квадратом ее математического ожидания:
   

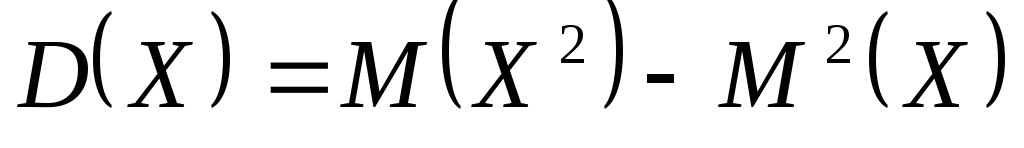
2. Дисперсия постоянной
   величины равна нулю.

3. Постоянный
   множитель можно выносить за знак
   дисперсии, возведя его в квадрат:
   

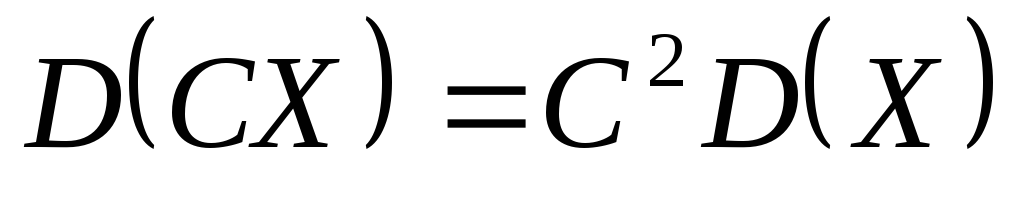
4. Дисперсия суммы
   двух независимых случайных величин
   равна сумме дисперсий этих величин:
   

5. Дисперсия разности
   двух независимых случайных величин
   равна сумме дисперсий этих величин:
   

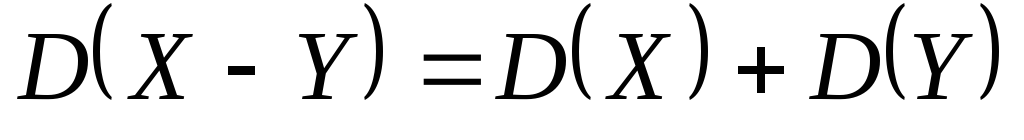
Пример.
Случайная величина X
задана плотностью вероятности. Определить
математическое ожидание, дисперсию и
среднее квадратическое отклонение
величины X.

,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?

Ответ на этот вопрос состоит из двух слов: с помощью интегралов.

Сам смысл математического ожидания и дисперсии мы уже разбирали ранее (но, конечно, повторим), и сейчас настало время узнать, как они определяются для непрерывной случайной величины. Всё очень просто, по аналогии с ДСВ:

Итак, все инструменты в руках и мы с энтузиазмом приступаем к любимому делу:

Задача 110
Непрерывная случайная величина  задана функцией

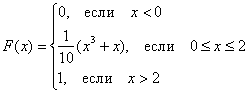
Вычислить . И построим ещё графики  и , ну а куда же без них? Повторение и ещё раз повторение!

Решение начнём как раз с графика функции распределения. При его ручном построении  удобно найти промежуточное значение  и аккуратно провести кусок кубической параболы :

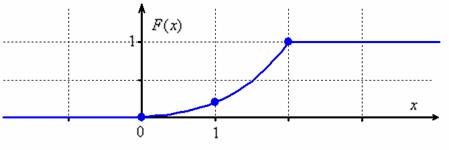
Повторяем: функция распределения  описывает вероятность того, что случайная величина  примет значение, МЕНЬШЕЕ, чем переменная , «пробегающая» все значения от  до .  Данная функция изменяется в пределах  и не убывает (т. к. «накапливает» вероятности). Но если в дискретном случае она разрывна (вспоминаем «ступеньки»), то здесь – всюду непрерывна!

Очевидно, что случайная величина  принимает случайные значения из отрезка , и какие из них более вероятны, а какие – менее, наглядно показывает функция ПЛОТНОСТИ распределения вероятностей:

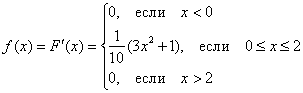
Найдём опорные точки параболы: , и готово:

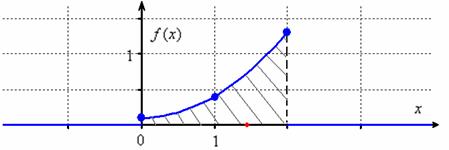
В отличие от , функции плотности может быть разрывна и может принимать значения бОльшие единицы (как в нашем случае); может, как убывать, так и возрастать и даже иметь экстремумы (наш кусок параболы растёт). Однако (повторяем), она неотрицательна:   и обладает свойством , и это лучше всегда проверять (а то мало ли, опечатка или ошибка). Неотрицательность функции очевидна по чертежу, а вот интеграл подлежит вычислению. Используя свойство аддитивности, делим его на три части:

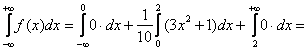
 – данный результат равен заштрихованной площади (см. выше) и с вероятностной точки зрения означает тот факт, что случайная величина  достоверно примет одно из значений отрезка . Причём, по чертежу хорошо видно, что значения из правой части отрезка гораздо более вероятны, чем значения слева.

И эти вероятности оцениваются кусками площади, а не значениями функции !!! (окончательно избавляемся от распространённой иллюзии)

Ради интереса вычислим:
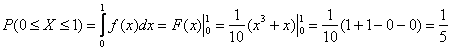 – вероятность того, что случайная величина  примет какое-нибудь значение из промежутка

Теперь числовые характеристики. Очевидно, что математическое ожидание (среднеожидаемое значение) случайной величины  должно находиться в «живом» отрезке , причём – ближе к его правому концу (поскольку там выше плотность вероятности).

Убедимся в этом аналитически. По формуле вычисления математического ожидания, и в силу того же свойства аддитивности:

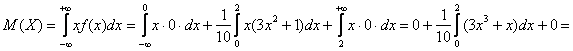
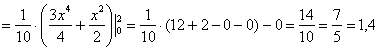 – ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.

! Примечание: в общем случае (и в этом, в частности)  не делит площадь на 2 равные части!

Если промежуток конечен, то можно сразу записывать, что матожидание равно определённому интегралу:
 

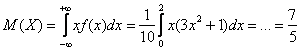
Дисперсию (меру рассеяния случайных значений относительно ) вычислим по формуле:

Сначала удобно разделаться с интегралом, здесь я не буду расписывать подробно:

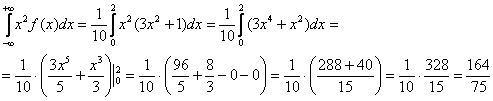
Таким образом:

И, наконец, среднее квадратическое отклонение:

Вот такое вот у нас получилось захватывающее повторение-изучение-исследование! И коль скоро спрашивалось немного, запишем:

ответ:

Строго говоря, ответ следовало записывать и в предыдущих задачах, но когда пунктов много, то итоговые результаты вполне допустимо помечать по ходу решения, например, подчёркивать или обводить карандашом.

Следующее задание для самостоятельного решения:

Задача 111
Дана функция:

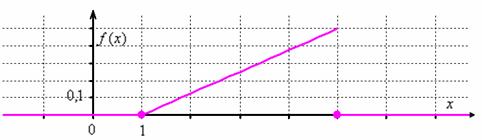
Представить  в аналитическом виде и показать, что она может служить плотностью вероятностей случайной величины . Вычислить  и 

Справка: уравнение прямой, проходящей через точки , можно составить по формуле .
Бывает, вычисление матожидания и дисперсии сопряжено с техническими трудностями, и в соответствующей статье сайта я рассмотрел следующие функции:

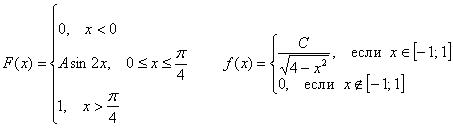
Однако вся трудность этих заданий состоит в более сложных интегралах, что, собственно, уже не относится к теории вероятностей, и посему я не включил эти примеры в настоящую книгу. Но вот задачка с несобственными интегралами не помешает:

Задача 112
Непрерывная случайная величина  задана плотностью распределения вероятностей:

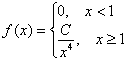
Найти  и . Составить функцию распределения и построить графики . Вычислить вероятность того, что случайная величина  примет значение, бОльшее, чем её математическое ожидание.

Попробуйте решить её самостоятельно! И для желающих есть более трудное задание с функцией  (смотрите опять же на сайте – ссылка выше).

Но этим всё дело не ограничивается. Точно так же, как и в дискретном случае, у непрерывной случайной величины существуют особые законы распределения вероятностей, и наиболее популярные из них мы рассмотрим прямо сейчас:

2.5.1. Равномерное распределение вероятностей

2.4.3. Функция ПЛОТНОСТИ распределения вероятностей

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин