Математическое ожидание случайной величины и его свойства
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Математическим ожиданием
дискретной случайной величины
, множество возможных значений которой
конечно, называется сумма произведений всех ее возможных значений на
соответствующие вероятности:
Если множество возможных
значений счетное, то
Причем математическое
ожидание существует, если ряд в правой части сходится абсолютно.
Математическое ожидание
приближенно равно среднему значению случайной величины.
Математическое ожидание непрерывной случайной величины
,
возможные значения которой принадлежат всей оси
,
определяется равенством:
где
– плотность распределения случайной величины
.
Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения принадлежат интервалу
,
то:
Все свойства математического ожидания, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.
Свойства математического ожидания
Свойство 1.
Математическое ожидание
константы равно этой константе:
Свойство 2.
Постоянный множитель
можно выносить за знак математического ожидания:
Свойство 3.
Математическое ожидание
суммы случайных величин равно сумме математических ожиданий слагаемых:
Свойство 4.
Математическое ожидания
произведения случайных величин:
где
–
ковариация случайных величин
и
В частности, если
и
независимы, то
И вообще, для независимых случайных величин
математическое ожидание их произведения равно произведению математических
ожиданий сомножителей:
Смежные темы решебника:
- Дисперсия и ее свойства. Среднее квадратическое отклонение
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Производится
3 выстрела с вероятностями попадания в цель, равными p1=0,4; p2=0,3 и p3=0,6. Найти математическое
ожидание общего числа попаданий.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Число
попаданий при первом выстреле есть случайная величина
, которая может принимать
только два значения:
1 –
попадание с вероятностью
0 –
промах с вероятностью
Математическое
ожидание числа попаданий при первом выстреле:
Аналогично
находим математические ожидания числа попаданий при втором и третьем выстрелах:
Общее
число попаданий есть также случайная величина, состоящая из суммы попаданий в
каждом из трех выстрелов:
Искомое
математическое ожидание:
Ответ:
Пример 2
Для случайных величин X,Y известны
характеристики M(X)=3, M(Y)=7, D(X)=16, D(Y)=49, ρXY=0.35
Найдите математическое ожидание M(XY).
Решение
Коэффициент корреляции:
Искомое математическое ожидание:
Ответ:
Пример 3
Даны законы распределения двух независимых
случайных величин X и Y:
Требуется:
–
составить закон распределения случайной величины Z=3X-Y;
– найти
числовые характеристики случайных величин X, Y, Z;
–
проверить свойство M(Z)=3M(X)-M(Y);
–
построить функцию распределения для
Z и построить ее график.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим закон распределения
:
или
Проверка:
Закон
распределения величины
:
Найдем математические
ожидания:
Проверим
свойство:
– выполняется
Найдем
дисперсии:
Средние
квадратические отклонения:
Запишем
функцию распределения:
График функции распределения
Пример 4
Найти
математическое ожидание суммы числа очков, которые могут выпасть при бросании
двух игральных костей.
Решение
Обозначим
число очков, которое может выпасть на первой кости, через
, и на второй – через
.
Возможные
значения этих величин одинаковы и равны: 1,2,3,4,5 и 6.
При этом
вероятность каждого из этих значений равна 1/6.
Математическое
ожидание числа очков, выпавших на первой кости:
Аналогично
математическое ожидание числа очков, выпавших на второй кости:
Искомое
математическое ожидание:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Найти
математическое ожидание случайной величины Z=6X-9Y+7XY-10, если известно, что
M(X)=2; M(Y)=3.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Случайные
величины X и Y независимы и распределены
равномерно: X – в интервале (a,b), Y
– в интервале (c,d).
Найти математическое ожидание случайной величины Z.
a=-3, b=4, c=3, d=6, Z=6XY, M(Z)-?
Задача 3
Найти
математическое ожидание и дисперсию случайной величины Z=3+2.2X-Y, где X и Y –
независимые случайные величины, если известны M(X)=1, D(X)=0.5,
M(Y)=2, D(Y)=2.
Задача 4
Независимые
случайные величины заданы законами распределения:
и
Построить ряд распределения F(Z), где Z=X-Y.
Проверить свойства:
M(Z)=M(X)-M(Y)
D(Z)=D(X)+D(Y)
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 5
Независимые
случайные величины X и Y заданы следующими законами
распределения:
и
Найти
математическое ожидание случайной величины XY
Задача 6
Дискретная
случайная величина X принимает три возможных значения: x1=4 с вероятностью p1=0.5; x2=6 c вероятностью p2=0.3 и x3 с вероятностью p3. Найти x3 и p3, зная, что M(X)=8.
Задача 7
Дан
перечень возможных значений случайной величины X: x1=-1, x2=0, x3=1, а также известны
математические ожидания этой величины и ее квадрата:
M(X)=0.1, M(X2)=0.9.
Найти
вероятности p1, p2, p3 соответствующие возможным
значениям x1, x2, x3.
Задача 8
Дан
перечень возможных значений дискретной случайной величины X:
x1=1, x2=2, x3=3
А также
известны математические ожидания этой величины и ее квадрата:
M(X)=2.3
M(X2)=5.9
Найти вероятности, соответствующие
возможным значениям X.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 октября 2021 года; проверки требуют 7 правок.
Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины[1]. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения (более строгие определения см. ниже). Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.
Обозначается через ![{mathbb {E}}[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa)
в русскоязычной литературе также встречается обозначение ![M[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/87b00856eb008c4ea9bc42894bb2bfa0b8605ac2)

Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно p — вероятности «единицы». Математическое ожидание суммы таких случайных величин равно np, где n — количество таких случайных величин. При этом вероятности появления определенного кол-ва единиц рассчитываются по биномиальному распределению. Поэтому в литературе, скорее всего, легче найти запись, что мат. ожидание биномиального распределения равно np[3].
Некоторые случайные величины не имеют математического ожидания, например, случайные величины, имеющие распределение Коши.
На практике математическое ожидание обычно оценивается как среднее арифметическое наблюдаемых значений случайной величины (выборочное среднее, среднее по выборке). Доказано, что при соблюдении определенных слабых условий (в частности, если выборка является случайной, то есть наблюдения являются независимыми) выборочное среднее стремится к истинному значению математического ожидания случайной величины при стремлении объема выборки (количества наблюдений, испытаний, измерений) к бесконечности.
Определение[править | править код]
Общее определение через интеграл Лебега[править | править код]
Пусть задано вероятностное пространство 




![M[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/87b00856eb008c4ea9bc42894bb2bfa0b8605ac2)
![{mathbb {E}}[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa)
Определение через функцию распределения случайной величины[править | править код]
Если 
,
.
Определение для абсолютно непрерывной случайной величины (через плотность распределения)[править | править код]
Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью 
.
Определение для дискретной случайной величины[править | править код]
Если 
,
,
то прямо из определения интеграла Лебега следует, что
.
Математическое ожидание целочисленной величины[править | править код]
- Если
— положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
,
,
,
то её математическое ожидание может быть выражено через производящую функцию последовательности 
как значение первой производной в единице: ![{displaystyle mathbb {E} [X]=P'(1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d2e607e95b3f1066a982f9ef824e923f80b3d13)


![{displaystyle P'(1)=mathbb {E} [X]=infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbcae4173f7ad0f9e03a817d06b36745b5110c8c)
Теперь возьмём производящую функцию 

,
Эта производящая функция связана с определённой ранее функцией 


Математическое ожидание случайного вектора[править | править код]
Пусть 
,
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины[править | править код]
Пусть 

если 
если 
Если распределение 

В специальном случае, когда 
![{displaystyle mathbb {E} [g(X)]=mathbb {E} [X^{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/304b08ae7de9b67c4c7c2a71c3e0e4129b89afbf)

Свойства математического ожидания[править | править код]
- Математическое ожидание числа (не случайной, фиксированной величины, константы) есть само число.
-
— константа;
- Математическое ожидание линейно[4], то есть
-
,
- где
— случайные величины с конечным математическим ожиданием, а
— произвольные константы;
В частности, математическое ожидание суммы (разности) случайных величин равно сумме (соответственно — разности) их математических ожиданий.
-
.
- Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если
почти наверняка, то
-
.
- Математическое ожидание произведения двух независимых или некоррелированных[5] случайных величин
равно произведению их математических ожиданий
-
.
Неравенства, связанные с математическим ожиданием[править | править код]
Неравенство Маркова — для неотрицательной случайной величины 


, где
.
Неравенство Йенсена для математического ожидания выпуклой функции от случайной величины. Пусть 



.
Теоремы, связанные с математическим ожиданием[править | править код]
.
.
Примеры[править | править код]
- Пусть случайная величина имеет дискретное равномерное распределение, то есть
Тогда её математическое ожидание
равно среднему арифметическому всех принимаемых значений.
.
- Пусть случайная величина
имеет стандартное распределение Коши. Тогда
,
то есть математическое ожидание 
См. также[править | править код]
- Дисперсия случайной величины
- Моменты случайной величины
- Условное математическое ожидание
Примечания[править | править код]
- ↑ «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — : «Советская энциклопедия», 1979. — 1104 с. — (51[03] М34). — 148 800 экз.
- ↑ А. Н. Ширяев. 1 // «Вероятность». — : МЦНМО, 2007. — 968 с. — ISBN 978-5-94057-036-3, 978-5-94057-106-3, 978-5-94057-105-6.
- ↑ В.Е.Гмурман. Часть вторая. Случайные величины. ->
Глава 4. Дискретные случайные величины. ->
Параграф 3. // [http://elenagavrile.narod.ru/ms/gmurman.pdf РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ]. — 1979. — С. 63. — 400 с. Архивная копия от 21 января 2022 на Wayback Machine - ↑ Пытьев Ю. П., Шишмарев И. А., Теория вероятностей, математическая статистика и элементы теории возможностей для физиков. — М.: Физический факультет МГУ, 2010.
- ↑ Теория вероятностей: 10.2. Теоремы о числовых характеристиках. sernam.ru. Дата обращения: 10 января 2018. Архивировано 10 января 2018 года.
Литература[править | править код]
- Феллер В. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Перевод с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова Под ред. Е. Б. Дынкина с предисловием А. Н. Колмогорова. — 2-е изд. — М.: Мир, 1964. — С. 270—272.
Ссылки[править | править код]
- Математическое ожидание и его свойства на http://www.toehelp.ru
Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Полезная страница? Сохрани или расскажи друзьям
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Лучшее спасибо – порекомендовать эту страницу
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Математическое ожидание
Данный калькулятор предназначен для вычисления математического ожидания дискретной случайной величины онлайн.
Оценка математического ожидания и дисперсии случайной величины имеет большое значение в теории вероятности.
Математическое ожидание – среднее значение случайной величины. Чтобы найти математическое ожидание случайной величины, следует вычислить сумму парных произведений всех возможных значений случайной величины на соответствующие им вероятности.
Свойства математического ожидания заключаются в следующем. Во-первых, математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий. Во-вторых, математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
Как найти среднее значение , формула (на примере следующих величин):
xi= 1 ; 2 ; 5 ; 6 (случайные величины)
pi = 0.1 ; 0.3 ; 0.1 ; 0.5 (вероятность)
M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 1×0.1 + 2×0.3 + 5×0.1 + 6×0.5 = 0.1 + 0.6 + 0.5 + 3 = 4.2
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
![]()
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
![]() .
.
Принимая во внимание свойства
математического ожидания, легко показать
что
![]()
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное![]() .
.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
![]() .
.
![]() =9
=9![]() =2,31.
=2,31.
![]() .
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
![]()
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
![]()
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
![]()
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
![]()
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
![]()
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:

Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до![]() .
.
Решение:
Для нахождения коэффициента авоспользуемся свойством![]() .
.
![]()
![]()
![]()
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
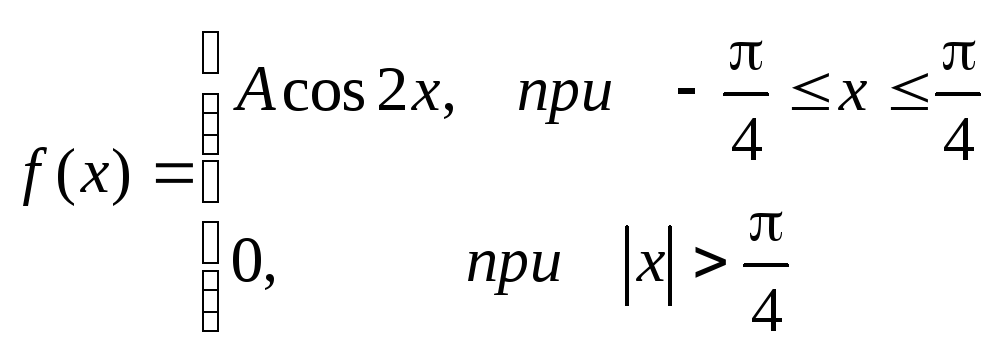
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал![]() .
.
Решение:
Найдем коэффициент А.
![]()
Найдем функцию распределения:
1) На участке
![]() :
:![]()
2) На участке
![]()
![]()
3) На участке
![]()
![]()
Итого:


Найдем вероятность попадания случайной
величины в интервал
![]() .
.
![]()
Ту же самую вероятность можно искать
и другим способом:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
![{displaystyle mathbb {E} [X]=int limits _{Omega }!X(omega ),mathbb {P} (domega ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c47eba9464e1dfddc4436d9220183b3ba849a36)


![{displaystyle mathbb {E} [X]=P'(1)=Q(1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0d04bcab881398d2122f343fdca9ae068506f71)
![{displaystyle mathbb {E} left[g(X)right]=sum limits _{i=1}^{infty }g(x_{i})p_{i},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cffa946f68de20938beb982930e5d0d6d24ff382)
![{displaystyle mathbb {E} left[g(X)right]=int limits _{-infty }^{infty }!g(x)f_{X}(x),dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bad706ef5dc04debc41d2b52b661a8d2fdabd06)
![{displaystyle mathbb {E} left[g(X)right]=int limits _{-infty }^{infty }!g(x),mathbb {P} ^{X}(dx).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b937706506d22524d36d963e9a1ae3a0a2b95a89)
![{displaystyle mathbb {E} [a]=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5b471aa432eab6dd8656039224530737a66e7f9)

![{displaystyle mathbb {E} [X]={frac {1}{n}}sum limits _{i=1}^{n}x_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10dff7b25a47f89fa59d7adade8131b235aeeecc)
