О вычислении матричной экспоненты
Время на прочтение
3 мин
Количество просмотров 16K

При построении и анализе поведения решений систем обыкновенных дифференциальных уравнений иногда требуется определять матричную экспоненту [1]. Классический метод связан с тем, что приходится рассчитывать большие степени матриц. В данном топике рассматривается алгоритм приближенного вычисления матричной экспоненты, который за фиксированное число матричных операций дает результат с заданной точностью. Проведен вычислительный эксперимент с целью анализа эффективности алгоритма.
1. Вычисление матричной экспоненты
Вычисление экспоненты
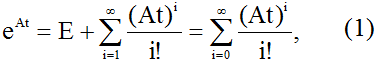
где E — единичная матрица, t — время, связано с необходимостью расчета высоких степеней матрица A. Получим формулу, позволяющую определить матричную экспоненту с помощью n степеней матрицы A (n — ее порядок).
Пусть характеристическое уравнение матрицы A имеет вид

По теореме Гамильтона-Кэли [2] матрица A удовлетворяет матричному уравнению, аналогичному (2):

откуда

Следуя методу Д.К. Фаддеева [2], коэффициенты характеристического уравнения определяются по рекуррентному соотношению

где  — след матрицы
— след матрицы 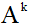 (сумма элементов, стоящих на главной диагонали),
(сумма элементов, стоящих на главной диагонали), 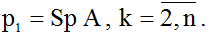
Далее введем обозначение: если m=0, то  ; иначе (при натуральном m)
; иначе (при натуральном m)

Умножим обе части соотношения (3) на матрицу A с учетом введенных обозначений. Получим

Выражение (5) можно переписать как

Теперь умножим обе части равенства (6) на матрицу A, подставив при этом в полученное соотношение формулу (3):

Тогда из выражения (7) с помощью последовательного умножения на матрицу A обеих его частей следует, что

Теперь представим матричную экспоненту как

Откуда имеем

2. Описание алгоритма
Для реализации вычисления матричной экспоненты, согласно (8), был применен следующий алгоритм. Сначала нужно инициировать результат значением нулевой матрицы. Вычислить 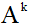 для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций:
для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций:
1. Вычислить сумму  . В качестве критерия прекращения суммирования использовать условие
. В качестве критерия прекращения суммирования использовать условие  , где
, где 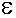 — положительное число, характеризующее точность вычисления суммы.
— положительное число, характеризующее точность вычисления суммы.
2. Используя значения, полученные ранее, определить произведение  и прибавить его к текущему значению результата.
и прибавить его к текущему значению результата.
При вычислении матричной экспоненты с помощью данного алгоритма используется рекуррентное соотношение (4). При больших значениях m и k большинство значений q будут рассчитываться повторно много раз. Поскольку q(m,k) является чистой функцией (зависит только от входных аргументов), то будет разумно применить стратегию мемоизации.
Мемоизация — оптимизационная техника, заключающаяся в запоминании результатов вычисления функции для предотвращения множественного расчета значения функции от одних и тех же аргументов. Данная оптимизация позволяет улучшить временные характеристики алгоритма за счет увеличения затрат памяти.
3. Сравнение с классическим алгоритмом
Разработанный алгоритм обеспечивает вычисление матричной экспоненты, используя только n степеней матрицы, в то время как классический алгоритм (1) не детерминирован, и вычисления степеней матрицы продолжаются, пока не выполнится условие останова алгоритма. Обычно таким условием является

Заметим, что классический алгоритм имеет потребление памяти  . Описанный алгоритм, в виду необходимости хранить n-1 степень матрицы A, имеет потребление памяти
. Описанный алгоритм, в виду необходимости хранить n-1 степень матрицы A, имеет потребление памяти  .
.
Нами был проведен вычислительный эксперимент с целью сравнить быстродействие алгоритмов. Для этого была разработана KipDblK программа из комплекса [3] на языке C++, реализующая оба алгоритма. С помощью данной программы были произведены расчеты матричной экспоненты для матриц различного размера. Порядок матрицы изменялся от 2 до 132. Матрица инициализировалась случайными числами в диапазоне [0;1]. Экспонента вычислялась для t=1. Результаты сравнительного эксперимента представлены на рис. 1. По оси абсцисс отложен порядок матрицы A, по оси ординат — время счета. Полученные точки соединены сплайнами для наглядности.

Рис. 1. Сравнение временных характеристик классического алгоритма (верхняя кривая) вычисления матричной экспоненты и алгоритма, описанного в данном топике (нижняя кривая).
P.S.
Данный топик был подготовлен по материалам нашей статьи [4].
Литература
1. Демидович Б.П. Лекции по математической теории устойчивости. — М.: Наука, 1967.
2. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967.
3. KipDblK maxima_comm.tar.gz.
4. Безгин С.В., Пчелинцев А.Н. Организация матричных и символьных вычислений для исследования поведения решений обыкновенных дифференциальных уравнений // Системы управления и информационные технологии, 2012. Т. 47, №1. — С. 4-7.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 мая 2020 года; проверки требуют 3 правки.
Экспонента матрицы — матричная функция от квадратной матрицы, аналогичная обычной экспоненциальной функции. Матричная экспонента устанавливает связь между алгеброй Ли матриц и соответствующий группой Ли.
Для вещественной или комплексной матрицы 





,
где 

Данный ряд всегда сходится, так что экспонента от 
Если 




Свойства[править | править код]
Основные свойства[править | править код]
Для комплексных матриц 






;
;
;
- если
, то
;
- если
— невырожденная матрица, то
.
, где
обозначает транспонированную матрицу для
, отсюда следует, что если
является симметричной, то
тоже симметрична, а если
— кососимметричная матрица, то
— ортогональная;
, где
обозначает эрмитово-сопряжённую матрицу для
, отсюда следует, что если
— эрмитова матрица, то
тоже эрмитова, а если
— антиэрмитова матрица, то
— унитарная
, где
— след матрицы
.
Системы линейных дифференциальных уравнений[править | править код]
Одна из причин, обуславливающих важность матричной экспоненты, заключается в том, что она может быть использована для решения систем обыкновенных дифференциальных уравнений[1]. Решение системы:
,
где 
Матричная экспонента может быть также использована для решения неоднородных уравнений вида
.
Не существует замкнутого аналитического выражения для решений неавтономных дифференциальных уравнений вида
,
где 
Экспонента суммы[править | править код]
Для любых двух вещественных чисел (скаляров) 







В общем случае из равенства 


Для эрмитовых матриц существует две примечательные теоремы, связанные со следом экспонент матриц.
Неравенство Голдена — Томпсона[править | править код]
Если 

,
Коммутативность для выполнения данного утверждения не требуется. Существуют контрпримеры, которые показывают, что неравенство Голдена — Томпсона не может быть расширено на три матрицы, а 



Теорема Либа[править | править код]
Теорема Либа, названная по имени Эллиотта Либа[en], гласит, что для фиксированной эрмитовой матрицы 
является вогнутой на конусе положительно-определённых матриц[3].
Экспоненциальное отображение[править | править код]
Экспонента матрицы всегда является невырожденной матрицей. Обратная к 

из пространства всех матриц размерности 




Для любых двух матриц 

,
где 

Отображение:
определяет гладкую кривую в полной линейной группе, которая проходит через единичный элемент при 
Приложения[править | править код]
Линейные дифференциальные уравнения[править | править код]
Пример однородной системы[править | править код]
Для системы:
её матрица есть:
Можно показать, что экспонента от матрицы 
таким образом, общее решение этой системы есть:
Пример неоднородной системы[править | править код]
Для решения неоднородной системы:
вводятся обозначения:
и
Так как сумма общего решения однородного уравнения и частного решения дают общее решение неоднородного уравнения, остаётся лишь найти частное решение. Так как:
где 
Обобщение: вариация произвольной постоянной[править | править код]
В случае неоднородной системы можно использовать метод вариации произвольной постоянной. Ищется частное решение в виде:

Чтобы 
Таким образом:
где 
См. также[править | править код]
- Тригонометрические функции от матрицы
Примечания[править | править код]
- ↑ Пискунов H. С. Дифференциальное и интегральное исчисления для втузов, т. 2.: Учебное пособие для втузов. — 13-е изд.. — М.: Наука, Главная редакция физико-математической литературы, 1985. — С. 544—547. — 560 с.
- ↑ Bhatia, R. Matrix Analysis (неопр.). — Springer, 1997. — Т. 169. — (Graduate Texts in Mathematics). — ISBN 978-0-387-94846-1.
- ↑ E. H. Lieb. Convex trace functions and the Wigner–Yanase–Dyson conjecture (англ.) // Adv. Math. : journal. — 1973. — Vol. 11, no. 3. — P. 267—288. — doi:10.1016/0001-8708(73)90011-X.
Ссылки[править | править код]
- Weisstein, Eric W., «Matrix Exponential», MathWorld
- Module for the Matrix Exponential
Другой метод
решения линейных систем с постоянными
коэффициентами основан на использовании
в качестве фундаментальной матрицы
матричной экспоненты
![]() Матрица
Матрица![]() определяется как сумма ряда
определяется как сумма ряда

Если матрица
![]() найдена, то решение системы (3.1) с
найдена, то решение системы (3.1) с
начальным условием![]() имеет вид
имеет вид![]() .
.
Для отыскания
матрицы
![]() могут быть применены различные приемы,
могут быть применены различные приемы,
в зависимости от структуры спектра
матрицы![]() .
.
-
Если все собственные
значения
 матрицы
матрицы – действительные различные числа, то
– действительные различные числа, то
матрицу удобно находить так:
удобно находить так:
![]() ,
,
(3.6)
где
![]() (матрица, составленная из столбцов
(матрица, составленная из столбцов
координат собственных векторов матрицыА),
а
 .
.
-
Если среди
различных собственных значений матрицы
А
имеются комплексные, то матрица
 в вещественной форме может быть найдена
в вещественной форме может быть найдена
с помощью следующего приема: нужно
найти общее решение системы (3.1) так,
как это было описано выше, а потом
составить матрицу,i-ым
столбцом которой будет решение этой
системы, удовлетворяющее начальным
условиям
 ,
, .
.
Пример 4.
Для матрицы системы из примера 2 найти
![]() .
.
Решение. Составим
матрицу
![]() из столбцов координат собственных
из столбцов координат собственных
векторов матрицы![]() :
:
 .
.
Тогда

 .
.
Пример 5. Для
матрицы
![]() найти
найти![]() .
.
Решение.
Собственные
значения матрицы
![]() – комплексно сопряженные числа
– комплексно сопряженные числа![]() .
.
Собственный вектор, соответствующий![]()
![]() .
.
Имеем:


Поэтому общее
решение линейной системы (3.2) с заданной
матрицей
![]() имеет вид
имеет вид

Найдем,
сначала
частное
решение,
удовлетворяющее
условию
![]() .
.
Оно будет иметь вид

Частное
решение,
удовлетворяющее
условиям
![]() ,имеет вид
,имеет вид

Поэтому
![]() .
.
-
Если среди
собственных значений матрица
 имеются кратные, то следует отыскать
имеются кратные, то следует отыскать
матрицу ,
,
приводящую матрицу к жордановой форме:
к жордановой форме:
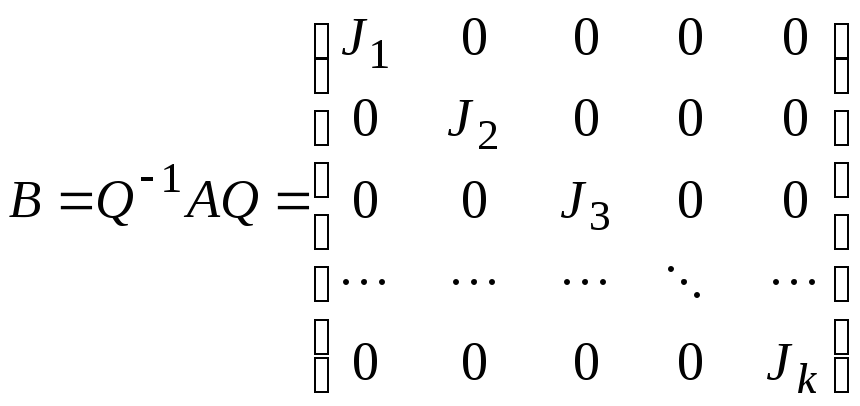 .
.
Жорданова
клетка
![]() ,
,
соответствующая
корню
![]() кратности
кратности
![]() ,имеет
,имеет
вид
 .
.
Для такой клетки
легко находится
 .
.
(3.7)
Проведя
такие
построения
для
каждой
клетки
Жордана,
находим
![]() .Тогда
.Тогда
![]() .
.
Пример
6.
Вычислить
матрицу
![]() ,
,
если![]() .
.
Решение.
Собственные значения данной матрицы
![]() .
.
Так как ранг матрицы![]() равен 1, то жорданова форма матрицыА
равен 1, то жорданова форма матрицыА
имеет вид
![]() .
.
Матрицу![]() ,
,
приводящую матрицуА
к жордановой форме, найдем из уравнения
![]() .
.
Пусть![]() .
.
Тогда
для
отыскания элементов матрицы
![]() получим уравнение
получим уравнение
![]() .
.
Это матричное
уравнение эквивалентно системе
![]() ,
,
решение которой
следующее:
![]() .
.
Итак,
![]() .
.
Согласно
формуле
(3.7)
![]() .
.
Поэтому
 (3.8)
(3.8)
3.2. Формула Коши
Решение неоднородной
системы с постоянными коэффициентами
![]() ,
,
(3.9)
удовлетворяющее
начальному условию
![]() ,
,
может быть выражено через экспоненциал
матрицы системы по формуле
![]() (3.10)
(3.10)
Если
решение системы (3.9) записано в виде
(3.10), то говорят, что оно записано в форме
Коши.
Пример
7.
Найдя матрицу
![]() ,
,
записать решение системы

в форме Коши.
Матрица
![]() для рассматриваемой системы уже была
для рассматриваемой системы уже была
найдена в предыдущем примере, и она
имеет вид (3.8). Согласно формуле (3.10),
можем записать

Задание 12
Решить линейную
систему путем сведения ее к одному
уравнению высшего порядка
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map between a matrix Lie algebra and the corresponding Lie group.
Let X be an n×n real or complex matrix. The exponential of X, denoted by eX or exp(X), is the n×n matrix given by the power series
where 


The above series always converges, so the exponential of X is well-defined. If X is a 1×1 matrix the matrix exponential of X is a 1×1 matrix whose single element is the ordinary exponential of the single element of X.
Properties[edit]
Elementary properties[edit]
Let X and Y be n×n complex matrices and let a and b be arbitrary complex numbers. We denote the n×n identity matrix by I and the zero matrix by 0. The matrix exponential satisfies the following properties.[2]
We begin with the properties that are immediate consequences of the definition as a power series:
- e0 = I
- exp(XT) = (exp X)T, where XT denotes the transpose of X.
- exp(X∗) = (exp X)∗, where X∗ denotes the conjugate transpose of X.
- If Y is invertible then eYXY−1 = YeXY−1.
The next key result is this one:
The proof of this identity is the same as the standard power-series argument for the corresponding identity for the exponential of real numbers. That is to say, as long as 





Consequences of the preceding identity are the following:
- eaXebX = e(a + b)X
- eXe−X = I
Using the above results, we can easily verify the following claims. If X is symmetric then eX is also symmetric, and if X is skew-symmetric then eX is orthogonal. If X is Hermitian then eX is also Hermitian, and if X is skew-Hermitian then eX is unitary.
Finally, a Laplace transform of matrix exponentials amounts to the resolvent,
for all sufficiently large positive values of s.
Linear differential equation systems[edit]
One of the reasons for the importance of the matrix exponential is that it can be used to solve systems of linear ordinary differential equations. The solution of
where A is a constant matrix, is given by
The matrix exponential can also be used to solve the inhomogeneous equation
See the section on applications below for examples.
There is no closed-form solution for differential equations of the form
where A is not constant, but the Magnus series gives the solution as an infinite sum.
The determinant of the matrix exponential[edit]
By Jacobi’s formula, for any complex square matrix the following trace identity holds:[3]

In addition to providing a computational tool, this formula demonstrates that a matrix exponential is always an invertible matrix. This follows from the fact that the right hand side of the above equation is always non-zero, and so det(eA) ≠ 0, which implies that eA must be invertible.
In the real-valued case, the formula also exhibits the map
to not be surjective, in contrast to the complex case mentioned earlier. This follows from the fact that, for real-valued matrices, the right-hand side of the formula is always positive, while there exist invertible matrices with a negative determinant.
Real symmetric matrices[edit]
The matrix exponential of a real symmetric matrix is positive definite. Let 

Since 




The exponential of sums[edit]
For any real numbers (scalars) x and y we know that the exponential function satisfies ex+y = ex ey. The same is true for commuting matrices. If matrices X and Y commute (meaning that XY = YX), then,
However, for matrices that do not commute the above equality does not necessarily hold.
The Lie product formula[edit]
Even if X and Y do not commute, the exponential eX + Y can be computed by the Lie product formula[4]
Using a large finite n to approximate the above is basis of the Suzuki-Trotter expansion, often used in numerical time evolution.
The Baker–Campbell–Hausdorff formula[edit]
In the other direction, if X and Y are sufficiently small (but not necessarily commuting) matrices, we have
where Z may be computed as a series in commutators of X and Y by means of the Baker–Campbell–Hausdorff formula:[5]
where the remaining terms are all iterated commutators involving X and Y. If X and Y commute, then all the commutators are zero and we have simply Z = X + Y.
Inequalities for exponentials of Hermitian matrices[edit]
For Hermitian matrices there is a notable theorem related to the trace of matrix exponentials.
If A and B are Hermitian matrices, then[6]
There is no requirement of commutativity. There are counterexamples to show that the Golden–Thompson inequality cannot be extended to three matrices – and, in any event, tr(exp(A)exp(B)exp(C)) is not guaranteed to be real for Hermitian A, B, C. However, Lieb proved[7][8] that it can be generalized to three matrices if we modify the expression as follows
The exponential map[edit]
The exponential of a matrix is always an invertible matrix. The inverse matrix of eX is given by e−X. This is analogous to the fact that the exponential of a complex number is always nonzero. The matrix exponential then gives us a map
from the space of all n×n matrices to the general linear group of degree n, i.e. the group of all n×n invertible matrices. In fact, this map is surjective which means that every invertible matrix can be written as the exponential of some other matrix[9] (for this, it is essential to consider the field C of complex numbers and not R).
For any two matrices X and Y,
where ‖ · ‖ denotes an arbitrary matrix norm. It follows that the exponential map is continuous and Lipschitz continuous on compact subsets of Mn(C).
The map
defines a smooth curve in the general linear group which passes through the identity element at t = 0.
In fact, this gives a one-parameter subgroup of the general linear group since
The derivative of this curve (or tangent vector) at a point t is given by
|
|
(1) |
The derivative at t = 0 is just the matrix X, which is to say that X generates this one-parameter subgroup.
More generally,[10] for a generic t-dependent exponent, X(t),

Taking the above expression eX(t) outside the integral sign and expanding the integrand with the help of the Hadamard lemma one can obtain the following useful expression for the derivative of the matrix exponent,[11]
The coefficients in the expression above are different from what appears in the exponential. For a closed form, see derivative of the exponential map.
Directional derivatives when restricted to Hermitian matrices[edit]
Let 











[12]
[13]
where 



In addition, for any 



where the matrix-valued function 

with
Computing the matrix exponential[edit]
Finding reliable and accurate methods to compute the matrix exponential is difficult, and this is still a topic of considerable current research in mathematics and numerical analysis. Matlab, GNU Octave, and SciPy all use the Padé approximant.[14][15][16] In this section, we discuss methods that are applicable in principle to any matrix, and which can be carried out explicitly for small matrices.[17] Subsequent sections describe methods suitable for numerical evaluation on large matrices.
Diagonalizable case[edit]
If a matrix is diagonal:
then its exponential can be obtained by exponentiating each entry on the main diagonal:
This result also allows one to exponentiate diagonalizable matrices. If
A = UDU−1
and D is diagonal, then
eA = UeDU−1.
Application of Sylvester’s formula yields the same result. (To see this, note that addition and multiplication, hence also exponentiation, of diagonal matrices is equivalent to element-wise addition and multiplication, and hence exponentiation; in particular, the “one-dimensional” exponentiation is felt element-wise for the diagonal case.)
Example : Diagonalizable[edit]
For example, the matrix
can be diagonalized as
Thus,
Nilpotent case[edit]
A matrix N is nilpotent if Nq = 0 for some integer q. In this case, the matrix exponential eN can be computed directly from the series expansion, as the series terminates after a finite number of terms:
Since the series has a finite number of steps, it is a matrix polynomial, which can be computed efficiently.
General case[edit]
Using the Jordan–Chevalley decomposition[edit]
By the Jordan–Chevalley decomposition, any 
where
- A is diagonalizable
- N is nilpotent
- A commutes with N
This means that we can compute the exponential of X by reducing to the previous two cases:
Note that we need the commutativity of A and N for the last step to work.
Using the Jordan canonical form[edit]
A closely related method is, if the field is algebraically closed, to work with the Jordan form of X. Suppose that X = PJP−1 where J is the Jordan form of X. Then
Also, since
Therefore, we need only know how to compute the matrix exponential of a Jordan block. But each Jordan block is of the form
where N is a special nilpotent matrix. The matrix exponential of J is then given by
Projection case[edit]
If P is a projection matrix (i.e. is idempotent: P2 = P), its matrix exponential is:
eP = I + (e − 1)P.
Deriving this by expansion of the exponential function, each power of P reduces to P which becomes a common factor of the sum:
Rotation case[edit]
For a simple rotation in which the perpendicular unit vectors a and b specify a plane,[18] the rotation matrix R can be expressed in terms of a similar exponential function involving a generator G and angle θ.[19][20]
The formula for the exponential results from reducing the powers of G in the series expansion and identifying the respective series coefficients of G2 and G with −cos(θ) and sin(θ) respectively. The second expression here for eGθ is the same as the expression for R(θ) in the article containing the derivation of the generator, R(θ) = eGθ.
In two dimensions, if ![{displaystyle a=left[{begin{smallmatrix}1\0end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19d56aced6e2c51dc00d64c3e48ad7877dfd5f72)
![{displaystyle b=left[{begin{smallmatrix}0\1end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b84e6c7fbab00f661b759ea592102d294e6c3393)
![{displaystyle G=left[{begin{smallmatrix}0&-1\1&0end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d66979defb968641217b24636f83ee2bd5c48135)
![{displaystyle G^{2}=left[{begin{smallmatrix}-1&0\0&-1end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a245a10c8a673650524b9f214b72dbcd04558c2e)
reduces to the standard matrix for a plane rotation.
The matrix P = −G2 projects a vector onto the ab-plane and the rotation only affects this part of the vector. An example illustrating this is a rotation of 30° = π/6 in the plane spanned by a and b,
Let N = I – P, so N2 = N and its products with P and G are zero. This will allow us to evaluate powers of R.
Evaluation by Laurent series[edit]
By virtue of the Cayley–Hamilton theorem the matrix exponential is expressible as a polynomial of order n−1.
If P and Qt are nonzero polynomials in one variable, such that P(A) = 0, and if the meromorphic function
is entire, then
To prove this, multiply the first of the two above equalities by P(z) and replace z by A.
Such a polynomial Qt(z) can be found as follows−see Sylvester’s formula. Letting a be a root of P, Qa,t(z) is solved from the product of P by the principal part of the Laurent series of f at a: It is proportional to the relevant Frobenius covariant. Then the sum St of the Qa,t, where a runs over all the roots of P, can be taken as a particular Qt. All the other Qt will be obtained by adding a multiple of P to St(z). In particular, St(z), the Lagrange-Sylvester polynomial, is the only Qt whose degree is less than that of P.
Example: Consider the case of an arbitrary 2×2 matrix,
The exponential matrix etA, by virtue of the Cayley–Hamilton theorem, must be of the form
(For any complex number z and any C-algebra B, we denote again by z the product of z by the unit of B.)
Let α and β be the roots of the characteristic polynomial of A,
Then we have
hence
if α ≠ β; while, if α = β,
so that
Defining
we have
where sin(qt)/q is 0 if t = 0, and t if q = 0.
Thus,

Thus, as indicated above, the matrix A having decomposed into the sum of two mutually commuting pieces, the traceful piece and the traceless piece,
the matrix exponential reduces to a plain product of the exponentials of the two respective pieces. This is a formula often used in physics, as it amounts to the analog of Euler’s formula for Pauli spin matrices, that is rotations of the doublet representation of the group SU(2).
The polynomial St can also be given the following “interpolation” characterization. Define et(z) ≡ etz, and n ≡ deg P. Then St(z) is the unique degree < n polynomial which satisfies St(k)(a) = et(k)(a) whenever k is less than the multiplicity of a as a root of P. We assume, as we obviously can, that P is the minimal polynomial of A. We further assume that A is a diagonalizable matrix. In particular, the roots of P are simple, and the “interpolation” characterization indicates that St is given by the Lagrange interpolation formula, so it is the Lagrange−Sylvester polynomial .
At the other extreme, if P = (z – a)n, then
The simplest case not covered by the above observations is when 
Evaluation by implementation of Sylvester’s formula[edit]
A practical, expedited computation of the above reduces to the following rapid steps. Recall from above that an n×n matrix exp(tA) amounts to a linear combination of the first n−1 powers of A by the Cayley–Hamilton theorem. For diagonalizable matrices, as illustrated above, e.g. in the 2×2 case, Sylvester’s formula yields exp(tA) = Bα exp(tα) + Bβ exp(tβ), where the Bs are the Frobenius covariants of A.
It is easiest, however, to simply solve for these Bs directly, by evaluating this expression and its first derivative at t = 0, in terms of A and I, to find the same answer as above.
But this simple procedure also works for defective matrices, in a generalization due to Buchheim.[21] This is illustrated here for a 4×4 example of a matrix which is not diagonalizable, and the Bs are not projection matrices.
Consider
with eigenvalues λ1 = 3/4 and λ2 = 1, each with a multiplicity of two.
Consider the exponential of each eigenvalue multiplied by t, exp(λit). Multiply each exponentiated eigenvalue by the corresponding undetermined coefficient matrix Bi. If the eigenvalues have an algebraic multiplicity greater than 1, then repeat the process, but now multiplying by an extra factor of t for each repetition, to ensure linear independence.
(If one eigenvalue had a multiplicity of three, then there would be the three terms: 
Sum all such terms, here four such,
To solve for all of the unknown matrices B in terms of the first three powers of A and the identity, one needs four equations, the above one providing one such at t = 0. Further, differentiate it with respect to t,
and again,
and once more,
(In the general case, n−1 derivatives need be taken.)
Setting t = 0 in these four equations, the four coefficient matrices Bs may now be solved for,
to yield
Substituting with the value for A yields the coefficient matrices
so the final answer is
The procedure is much shorter than Putzer’s algorithm sometimes utilized in such cases.
Illustrations[edit]
Suppose that we want to compute the exponential of
Its Jordan form is
where the matrix P is given by
Let us first calculate exp(J). We have
The exponential of a 1×1 matrix is just the exponential of the one entry of the matrix, so exp(J1(4)) = [e4]. The exponential of J2(16) can be calculated by the formula e(λI + N) = eλ eN mentioned above; this yields[22]
Therefore, the exponential of the original matrix B is
Applications[edit]
Linear differential equations[edit]
The matrix exponential has applications to systems of linear differential equations. (See also matrix differential equation.) Recall from earlier in this article that a homogeneous differential equation of the form
has solution eAt y(0).
If we consider the vector
we can express a system of inhomogeneous coupled linear differential equations as
Making an ansatz to use an integrating factor of e−At and multiplying throughout, yields
The second step is possible due to the fact that, if AB = BA, then eAtB = BeAt. So, calculating eAt leads to the solution to the system, by simply integrating the third step with respect to t.
A solution to this can be obtained by integrating and multiplying by 



Example (homogeneous)[edit]
Consider the system
The associated defective matrix is
The matrix exponential is
so that the general solution of the homogeneous system is
amounting to
Example (inhomogeneous)[edit]
Consider now the inhomogeneous system
We again have
and
From before, we already have the general solution to the homogeneous equation. Since the sum of the homogeneous and particular solutions give the general solution to the inhomogeneous problem, we now only need find the particular solution.
We have, by above,
which could be further simplified to get the requisite particular solution determined through variation of parameters.
Note c = yp(0). For more rigor, see the following generalization.
Inhomogeneous case generalization: variation of parameters[edit]
For the inhomogeneous case, we can use integrating factors (a method akin to variation of parameters). We seek a particular solution of the form yp(t) = exp(tA) z(t),
For yp to be a solution,
Thus,
where c is determined by the initial conditions of the problem.
More precisely, consider the equation
with the initial condition Y(t0) = Y0, where
Left-multiplying the above displayed equality by e−tA yields
We claim that the solution to the equation
with the initial conditions 
where the notation is as follows:
sk(t) is the coefficient of 
![S_tinmathbb{C}[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/600abf70e16defa72aa00bb637b53ca1d04049b5)
To justify this claim, we transform our order n scalar equation into an order one vector equation by the usual reduction to a first order system. Our vector equation takes the form
where A is the transpose companion matrix of P. We solve this equation as explained above, computing the matrix exponentials by the observation made in Subsection Evaluation by implementation of Sylvester’s formula above.
In the case n = 2 we get the following statement. The solution to
is
where the functions s0 and s1 are as in Subsection Evaluation by Laurent series above.
Matrix-matrix exponentials[edit]
The matrix exponential of another matrix (matrix-matrix exponential),[23] is defined as
for any normal and non-singular n×n matrix X, and any complex n×n matrix Y.
For matrix-matrix exponentials, there is a distinction between the left exponential YX and the right exponential XY, because the multiplication operator for matrix-to-matrix is not commutative. Moreover,
- If X is normal and non-singular, then XY and YX have the same set of eigenvalues.
- If X is normal and non-singular, Y is normal, and XY = YX, then XY = YX.
- If X is normal and non-singular, and X, Y, Z commute with each other, then XY+Z = XY·XZ and Y+ZX = YX·ZX.
See also[edit]
- Matrix function
- Matrix logarithm
- C0-semigroup
- Exponential function
- Exponential map (Lie theory)
- Magnus expansion
- Derivative of the exponential map
- Vector flow
- Golden–Thompson inequality
- Phase-type distribution
- Lie product formula
- Baker–Campbell–Hausdorff formula
- Frobenius covariant
- Sylvester’s formula
- Trigonometric functions of matrices
References[edit]
- ^ Hall 2015 Equation 2.1
- ^ Hall 2015 Proposition 2.3
- ^ Hall 2015 Theorem 2.12
- ^ Hall 2015 Theorem 2.11
- ^ Hall 2015 Chapter 5
- ^ Bhatia, R. (1997). Matrix Analysis. Graduate Texts in Mathematics. Vol. 169. Springer. ISBN 978-0-387-94846-1.
- ^ E. H. Lieb (1973). “Convex trace functions and the Wigner–Yanase–Dyson conjecture”. Advances in Mathematics. 11 (3): 267–288. doi:10.1016/0001-8708(73)90011-X.
- ^ H. Epstein (1973). “Remarks on two theorems of E. Lieb”. Communications in Mathematical Physics. 31 (4): 317–325. Bibcode:1973CMaPh..31..317E. doi:10.1007/BF01646492. S2CID 120096681.
- ^ Hall 2015 Exercises 2.9 and 2.10
- ^ R. M. Wilcox (1967). “Exponential Operators and Parameter Differentiation in Quantum Physics”. Journal of Mathematical Physics. 8 (4): 962–982. Bibcode:1967JMP…..8..962W. doi:10.1063/1.1705306.
- ^ Hall 2015 Theorem 5.4
- ^ Lewis, Adrian S.; Sendov, Hristo S. (2001). “Twice differentiable spectral functions” (PDF). SIAM Journal on Matrix Analysis and Applications. 23 (2): 368–386. doi:10.1137/S089547980036838X. See Theorem 3.3.
- ^ a b Deledalle, Charles-Alban; Denis, Loïc; Tupin, Florence (2022). “Speckle reduction in matrix-log domain for synthetic aperture radar imaging”. Journal of Mathematical Imaging and Vision. 64 (3): 298–320. doi:10.1007/s10851-022-01067-1. See Propositions 1 and 2.
- ^ “Matrix exponential – MATLAB expm – MathWorks Deutschland”. Mathworks.de. 2011-04-30. Retrieved 2013-06-05.
- ^ “GNU Octave – Functions of a Matrix”. Network-theory.co.uk. 2007-01-11. Archived from the original on 2015-05-29. Retrieved 2013-06-05.
- ^ “scipy.linalg.expm function documentation”. The SciPy Community. 2015-01-18. Retrieved 2015-05-29.
- ^ See Hall 2015 Section 2.2
- ^ in a Euclidean space
- ^ Weyl, Hermann (1952). Space Time Matter. Dover. p. 142. ISBN 978-0-486-60267-7.
- ^ Bjorken, James D.; Drell, Sidney D. (1964). Relativistic Quantum Mechanics. McGraw-Hill. p. 22.
- ^ Rinehart, R. F. (1955). “The equivalence of definitions of a matric function”. The American Mathematical Monthly, 62 (6), 395-414.
- ^ This can be generalized; in general, the exponential of Jn(a) is an upper triangular matrix with ea/0! on the main diagonal, ea/1! on the one above, ea/2! on the next one, and so on.
- ^ Ignacio Barradas and Joel E. Cohen (1994). “Iterated Exponentiation, Matrix-Matrix Exponentiation, and Entropy” (PDF). Academic Press, Inc. Archived from the original (PDF) on 2009-06-26.
- Hall, Brian C. (2015), Lie groups, Lie algebras, and representations: An elementary introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3-319-13466-6
- Horn, Roger A.; Johnson, Charles R. (1991). Topics in Matrix Analysis. Cambridge University Press. ISBN 978-0-521-46713-1..
- Moler, Cleve; Van Loan, Charles F. (2003). “Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later” (PDF). SIAM Review. 45 (1): 3–49. Bibcode:2003SIAMR..45….3M. CiteSeerX 10.1.1.129.9283. doi:10.1137/S00361445024180. ISSN 1095-7200..
- Suzuki, Masuo (1985). “Decomposition formulas of exponential operators and Lie exponentials with some applications to quantum mechanics and statistical physics”. Journal of Mathematical Physics. 26 (4): 601–612. Bibcode:1985JMP….26..601S. doi:10.1063/1.526596.
- Curtright, T L; Fairlie, D B; Zachos, C K (2014). “A compact formula for rotations as spin matrix polynomials”. Symmetry, Integrability and Geometry: Methods and Applications. 10: 084. arXiv:1402.3541. Bibcode:2014SIGMA..10..084C. doi:10.3842/SIGMA.2014.084. S2CID 18776942.
- Householder, Alston S. (2006). The Theory of Matrices in Numerical Analysis. Dover Books on Mathematics. ISBN 978-0-486-44972-2.
- Van Kortryk, T. S. (2016). “Matrix exponentials, SU(N) group elements, and real polynomial roots”. Journal of Mathematical Physics. 57 (2): 021701. arXiv:1508.05859. Bibcode:2016JMP….57b1701V. doi:10.1063/1.4938418. S2CID 119647937.
External links[edit]
- Weisstein, Eric W. “Matrix Exponential”. MathWorld.
1. Экспонента квадратной матрицы формально определяется как сумма ряда:
где есть единичная матрица соответствующего размера.
Из этого определения несложно получить ряд свойств экспоненты, некоторые из которых перечислены ниже:
- Экспонента нулевой матрицы есть единичная матрица.
- Транспонирование (а также эрмитово сопряжение) перестановочно с экспоненцированием:
.
- Если
симметрична (эрмитова), то и
симметрична (эрмитова).
- Если
, то
и
. В частности,
.
- Матрица
всегда обратима:
.
- Для любой обратимой матрицы
верно
.
- Экспонента диагональной матрицы
также является диагональной матрицей
.
- Последнее свойство обобщается на блочно-диагональные матрицы. Пусть
, где каждая
есть квадратная матрица. Тогда экспонента также является блочно-диагональной матрицей:
.
Таким образом, если матрица диагонализируема, т.е. если найдётся такая матрица
, что
, где
— диагональная матрица (матрица собственных значений), то после выполнения диагонализации (eigendecomposition)
вычислить её экспоненту не составит труда.
К сожалению, не все матрицы диагонализируемы, хотя для матриц над полем комплексных чисел множество недиагонализируемых матриц есть множество меры нуль. Поэтому, кстати, даже экспоненту вещественнозначной матрицы может быть удобнее вычислять в комплексных числах. Те, кто хорошо учил линейную алгебру, вспомнят о «жордановой форме», которая существует для любой матрицы и представляет собой как раз блочно-диагональную матрицу, составленную из блоков, называемых «жордановы клетки». Это означает, что если у нас есть представление , где
, и если мы умеем вычислять экспоненту жордановой клетки, то мы опять же без проблем вычислим экспоненту исходной матрицы. Ниже я коснусь вопроса вычисления экспоненты жордановой клетки.
Особняком стоит свойство, известное как «формула Якоби». Его можно применять, например, для проверки качества вычисления матричной экспоненты:
2. Вычисление экспоненты прямым суммированием ряда традиционно считается «плохим методом». На самом деле, главный его недостаток заключается в низкой скорости вычислений, но не в точности. Важно организовать этот процесс правильно! В своей практике я применял следующие приёмы:
Я не претендую на то, что это лучший способ вычислять данную сумму. Но исходя из моего (ограниченного) опыта, этот способ достаточно надёжен и сравнительно прост в реализации. В моей практике собственно скорость вычисления экспоненты не играла большой роли. А точность была важна.
3. Экспонента жордановой клетки. Жорданова клетка (в случае комплексных чисел) есть квадратная матрица, на главной диагонали которой стоит некое число
(любое значение, но одно во всех позициях диагонали), на первой наддиагонали стоят единицы, а все прочие элементы — нули:
Заметим, что , где
— шаровая матрица (диагональная с одинаковыми значениями на диагонали), а
— нильпотентна, поскольку
(здесь и ниже
— размер
). Более того, легко заметить, что домножение
на
попросту сдвигает единичную наддиагональ на одну позицию вверх. Поэтому имеем
Ну и по свойствам экспоненты и шаровых матриц имеем
В случае наличия скалярного множителя :
где
К сожалению, вычисление жордановой формы как численный метод обладает врождённым недостатком: чувствительностью к сколь угодно малым изменениям исходной матрицы. Из чего можно сделать вывод, что на практике может быть разумно вносить в недиагонализируемую матрицу малые возмущения с целью получить диагонализируемую матрицу.
4. О вычислении матричной экспоненты (и иных функций, определяемых как сумма ряда) с помощью комбинирования разложения Шура, рекуррентных соотношений Сильвестра и суммировании ряда см. Davies, Higham. A Schur-Parlett Algorithm for Computing Matrix Functions.









![A=left[{begin{array}{rrr}2&-1&1\0&3&-1\2&1&3end{array}}right]~,](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5a866884769332fa1a366783b9a1d1955f7dc05)





![{begin{aligned}{mathbf {y}}_{p}'(t)&=(e^{{tA}})'{mathbf {z}}(t)+e^{{tA}}{mathbf {z}}'(t)\[6pt]&=Ae^{{tA}}{mathbf {z}}(t)+e^{{tA}}{mathbf {z}}'(t)\[6pt]&=A{mathbf {y}}_{p}(t)+e^{{tA}}{mathbf {z}}'(t)~.end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ade2a91c46e5fb7cec318107f6f7e4c99a7fe943)
![{begin{aligned}e^{{tA}}{mathbf {z}}'(t)&={mathbf {b}}(t)\[6pt]{mathbf {z}}'(t)&=(e^{{tA}})^{{-1}}{mathbf {b}}(t)\[6pt]{mathbf {z}}(t)&=int _{0}^{t}e^{{-uA}}{mathbf {b}}(u),du+{mathbf {c}}~.end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28f09b0f45bee4e56ae6c7ecc9200f3d2b5d6953)
























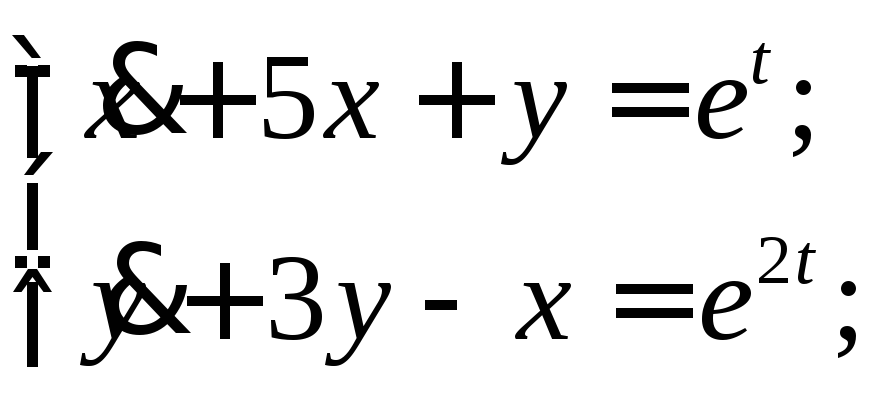

















![{displaystyle Z=X+Y+{frac {1}{2}}[X,Y]+{frac {1}{12}}[X,[X,Y]]-{frac {1}{12}}[Y,[X,Y]]+cdots ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ebd57eb47ed56f6d8111bbd7dc460e0242019b4)
![{displaystyle operatorname {tr} exp(A+B)leq operatorname {tr} left[exp(A)exp(B)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a67f5a9c156589dcc0627529aeb987b7ab57ff77)
![{displaystyle operatorname {tr} exp(A+B+C)leq int _{0}^{infty }mathrm {d} t,operatorname {tr} left[e^{A}left(e^{-B}+tright)^{-1}e^{C}left(e^{-B}+tright)^{-1}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8395467e8b32cac1f2fd5634a920770cb7eca5e)



![{displaystyle left({frac {d}{dt}}e^{X(t)}right)e^{-X(t)}={frac {d}{dt}}X(t)+{frac {1}{2!}}left[X(t),{frac {d}{dt}}X(t)right]+{frac {1}{3!}}left[X(t),left[X(t),{frac {d}{dt}}X(t)right]right]+cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c74b020fc5a663d2e643610b3dc6a5d3e9ee0c8)
![{displaystyle Dexp(X)[V]triangleq lim _{epsilon to 0}{frac {1}{epsilon }}left(displaystyle e^{X+epsilon V}-e^{X}right)=E(Godot {bar {V}})E^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/720434d760d91904b61a54c17630773a2adee785)

![{displaystyle D^{2}exp(X)[U,V]triangleq lim _{epsilon _{u}to 0}lim _{epsilon _{v}to 0}{frac {1}{4epsilon _{u}epsilon _{v}}}left(displaystyle e^{X+epsilon _{u}U+epsilon _{v}V}-e^{X-epsilon _{u}U+epsilon _{v}V}-e^{X+epsilon _{u}U-epsilon _{v}V}+e^{X-epsilon _{u}U-epsilon _{v}V}right)=EF(U,V)E^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60283f8a1d7b8a53fd09a079916761b54b40d524)
















































![{displaystyle {begin{aligned}&exp left({begin{bmatrix}16&1\0&16end{bmatrix}}right)=e^{16}exp left({begin{bmatrix}0&1\0&0end{bmatrix}}right)=\[6pt]{}={}&e^{16}left({begin{bmatrix}1&0\0&1end{bmatrix}}+{begin{bmatrix}0&1\0&0end{bmatrix}}+{1 over 2!}{begin{bmatrix}0&0\0&0end{bmatrix}}+cdots {}right)={begin{bmatrix}e^{16}&e^{16}\0&e^{16}end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/645acc0496a216b8b6bd59c4f7bc8ba0023e82d4)
![{displaystyle {begin{aligned}exp(B)&=Pexp(J)P^{-1}=P{begin{bmatrix}e^{4}&0&0\0&e^{16}&e^{16}\0&0&e^{16}end{bmatrix}}P^{-1}\[6pt]&={1 over 4}{begin{bmatrix}13e^{16}-e^{4}&13e^{16}-5e^{4}&2e^{16}-2e^{4}\-9e^{16}+e^{4}&-9e^{16}+5e^{4}&-2e^{16}+2e^{4}\16e^{16}&16e^{16}&4e^{16}end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf04ed9a5767fa06004d8c32cb391df66373de5b)







![{displaystyle {begin{aligned}2x&=x(0)e^{2t}left(1+e^{2t}-2tright)+y(0)left(-2te^{2t}right)+z(0)e^{2t}left(-1+e^{2t}right)\[2pt]2y&=x(0)left(-e^{2t}right)left(-1+e^{2t}-2tright)+y(0)2(t+1)e^{2t}+z(0)left(-e^{2t}right)left(-1+e^{2t}right)\[2pt]2z&=x(0)e^{2t}left(-1+e^{2t}+2tright)+y(0)2te^{2t}+z(0)e^{2t}left(1+e^{2t}right)~.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37743b1b3b11a50a71b628fede06041391b9c98)


![{displaystyle {begin{aligned}mathbf {y} _{p}&=e^{tA}int _{0}^{t}e^{(-u)A}{begin{bmatrix}e^{2u}\0\e^{2u}end{bmatrix}},du+e^{tA}mathbf {c} \[6pt]&=e^{tA}int _{0}^{t}{begin{bmatrix}2e^{u}-2ue^{2u}&-2ue^{2u}&0\-2e^{u}+2(u+1)e^{2u}&2(u+1)e^{2u}&0\2ue^{2u}&2ue^{2u}&2e^{u}end{bmatrix}}{begin{bmatrix}e^{2u}\0\e^{2u}end{bmatrix}},du+e^{tA}mathbf {c} \[6pt]&=e^{tA}int _{0}^{t}{begin{bmatrix}e^{2u}left(2e^{u}-2ue^{2u}right)\e^{2u}left(-2e^{u}+2(1+u)e^{2u}right)\2e^{3u}+2ue^{4u}end{bmatrix}},du+e^{tA}mathbf {c} \[6pt]&=e^{tA}{begin{bmatrix}-{1 over 24}e^{3t}left(3e^{t}(4t-1)-16right)\{1 over 24}e^{3t}left(3e^{t}(4t+4)-16right)\{1 over 24}e^{3t}left(3e^{t}(4t-1)-16right)end{bmatrix}}+{begin{bmatrix}2e^{t}-2te^{2t}&-2te^{2t}&0\-2e^{t}+2(t+1)e^{2t}&2(t+1)e^{2t}&0\2te^{2t}&2te^{2t}&2e^{t}end{bmatrix}}{begin{bmatrix}c_{1}\c_{2}\c_{3}end{bmatrix}}~,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ef0cccdaf2d5b0fe9d53a321c37fdde8f71b782)
![{displaystyle {begin{aligned}mathbf {y} _{p}'(t)&=left(e^{tA}right)'mathbf {z} (t)+e^{tA}mathbf {z} '(t)\[6pt]&=Ae^{tA}mathbf {z} (t)+e^{tA}mathbf {z} '(t)\[6pt]&=Amathbf {y} _{p}(t)+e^{tA}mathbf {z} '(t)~.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1870f9bb07a06edb36c925a5612cc28d61d36722)
![{displaystyle {begin{aligned}e^{tA}mathbf {z} '(t)&=mathbf {b} (t)\[6pt]mathbf {z} '(t)&=left(e^{tA}right)^{-1}mathbf {b} (t)\[6pt]mathbf {z} (t)&=int _{0}^{t}e^{-uA}mathbf {b} (u),du+mathbf {c} ~.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8517346e558b122ce5039cdeb54006e7e0e7eb18)










