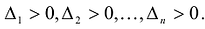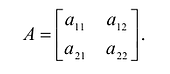-
Квадратичные формы
-
Матрица квадратичной формы
Определение.
Квадратичной формой Ĺ(х1,х2,…,хп)
от n переменных называется сумма, каждый
член которой является или квадратом
одной из переменных или произведением
двух разных переменных, взятых с
некоторыми коэффициентами – действительными
числами.
Мы будем рассматривать квадратичные
формы с двумя переменными
(5.1.1)
и с
тремя переменными
(5.1.2)
Квадратичные
формы можно записать в матричной форме,
введя в рассмотрение матрицу А квадратичной
формы. Для (5.1.1) матрица имеет вид
Для (5.1.2) матрица записывается в виде:
А=
То
есть матрица квадратичной формы является
симметрической матрицей. Для переменных
вводится матрица-столбец Х и
транспонированная
–
матрица – строка. Тогда квадратичная
форма может быть записана в виде
произведения трех матриц
( 5.1.3)
Пример.
Дана квадратичная
форма
Записать ее в матричной форме.
Решение.
Матрица квадратичной формы составляется
следующим образом: элементы главной
диагонали равны коэффициентам при
квадратах переменных, остальные элементы
равны половине коэффициента при
произведении х1х2:
А=
Матрица Х=
Таким
образом,
Пример.
Написать матрицу квадратичной формы
Решение.
На главной диагонали располагаем
элементы при квадратах переменных
а11=3,
а22=1,
а33=6,
остальные элементы а12=а21=5/2,
а13=а31=-2,
а23=а32=0.
Следовательно,
А=
Ранг матрицы квадратичной формы называют
рангом квадратичной формы. Если ранг
совпадает с числом переменных квадратичной
формы, то ее называют невырожденной.
Если ранг меньше, то квадратичная форма
– вырожденная.
Пример.
Является ли невырожденной квадратичная
форма L(х1,х2,х3
) = х21+4х1х3?
Решение.
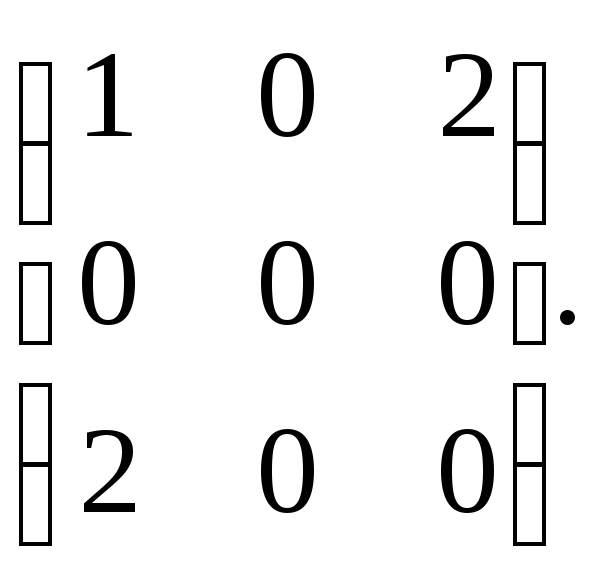
Составим матрицу квадратичной формы
А=
Найдем ранг матрицы А. Так как величина
ранга не зависит от элементарных
преобразований матрицы, то отбрасывая
нулевую строку, найдем минор второго
порядка М2=
то есть ранг меньше трех переменных,
входящих в квадратичную форму.
Следовательно, данная квадратичная
форма вырожденная.
-
Канонический вид квадратичной формы
В
квадратичной форме
можно выполнить линейное преобразование
переменных
невырожденная
квадратная матрица n-ого порядка. Учитывая
линейное преобразование переменных,
получим равенство:
(5.2.1)
Здесь
использовано свойство
.
Новая матрица квадратичной формы
( 5.2.2)
Первоначальная квадратичная форма и
полученная из нее (5.2.1) с помощью
невырожденного линейного преобразования
называются эквивалентными квадратичными
формами.
Пример.
Дана квадратичная форма
.
Найти эквивалентную квадратичную форму
L(y1,y2),
используя линейное преобразование
переменных х1=у1-2у2,
х2=у1+у2.
Решение.
По условию матрица данной квадратичной
формы А=
Заданное линейное преобразование в
матричной форме
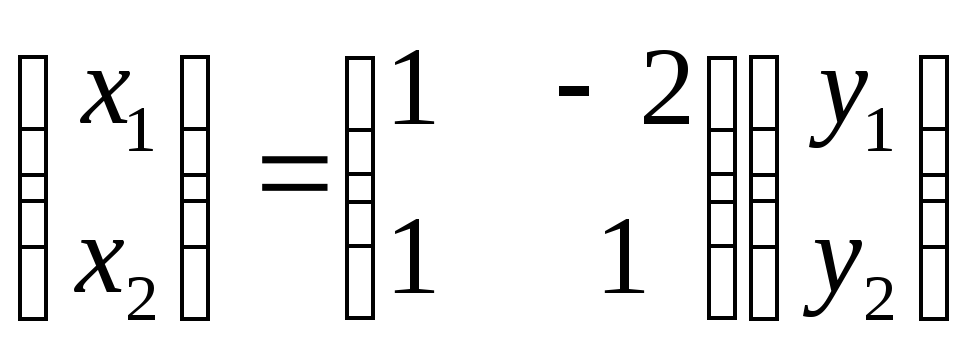
Следовательно,
матрица С=
Теперь
по формуле (5.2.2) новая матрица получается
Ответ.
Квадратичная форма, эквивалентная
данной
Определение.
Квадратичная форма имеет канонический
вид, если все коэффициенты
,
т.е.
и ее матрица является диагональной.
В примере после линейного преобразования
квадратичная форма приняла канонический
вид.
Справедливо следующее утверждение:
любая квадратичная форма с помощью
невырожденного линейного преобразования
переменных может быть приведена к
каноническому виду. Возможны два способа
приведения квадратичных форм к
каноническому виду.
Первый
способ. Идея
метода состоит в том, что путем
тождественных преобразований в
квадратичной форме последовательно
выделяются полные квадраты по всем
переменным.
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Выделим полный квадрат по переменной
х1:
Введя
новые переменные у1=х1–получим
канонический вид
Пример.
Привести к каноническому виду
квадратичную форму
Решение.
Сначала сгруппируем все слагаемые,
содержащие х1,
и затем дополним их до полного квадрата:
Теперь
полный квадрат по х1
оставляем неизменным, а среди оставшихся
слагаемых объединяем все члены, содержащие
х2,
и выделяем полный квадрат:
Обозначим
у1=х1+2х2+2х3,
у2=х2+х3,
у3=х3,
в результате
получаем канонический вид
Второй
способ. Матрица
квадратичной формы всегда симметрическая,
поэтому она имеет действительные
собственные значения и сводится к
диагональному виду с помощью линейного
ортогонального преобразования Х=QY,
где Q
– ортогональная матрица (см. пример в
4.4.1)
Если
квадратичная форма зависит от двух
переменных L=L(x1,x2)
и λ1,λ2
собственные значения ее матрицы , то
канонический вид квадратичной формы
Если
L=L(x1,x2,x3)
и ее матрица имеет собственные значения
λ1,
λ2,
λ3
, то кононический вид в новых переменных
Чтобы найти линейное преобразование
переменных, приводящих квадратичную
форму к каноническому виду, нужно найти
собственные векторы, нормировать их и
записать матрицу Q.
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Матрица данной квадратичной формы
А=.
Характеристическое уравнение
.
Собственные
значения λ1=1,λ2=5.
Квадратичная форма в новом базисе из
собственных векторов имеет канонический
вид
Найдем
собственные векторы. Для этого в систему
уравнений вида (4.3.2)
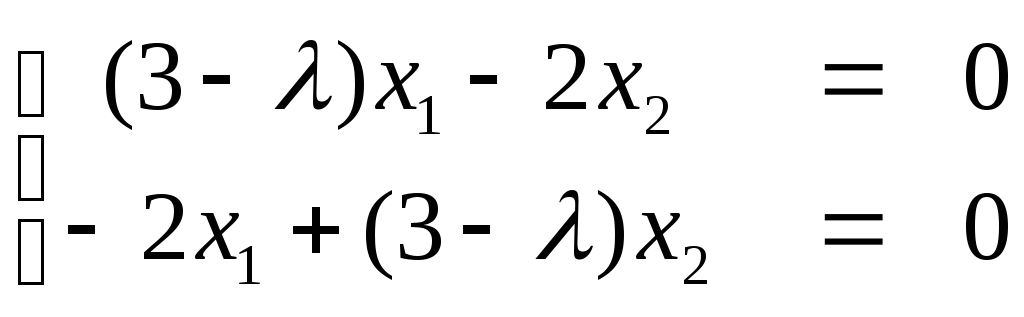
подставим собственные значения.
а)
При λ=λ1=1
получим
Пусть
х2=1
и х1=1.
Тогда е1=(1,1).
б)
При λ=λ2=5
система имеет вид
Таким
образом, х1=-х2
и за второй собственный вектор можно
взять е2=(-1,1).
Очевидно, что е1е2=0
– векторы ортогональны. Нормируя е1,
е2,
запишем ортонормированный базис:
е1=(
Матрица
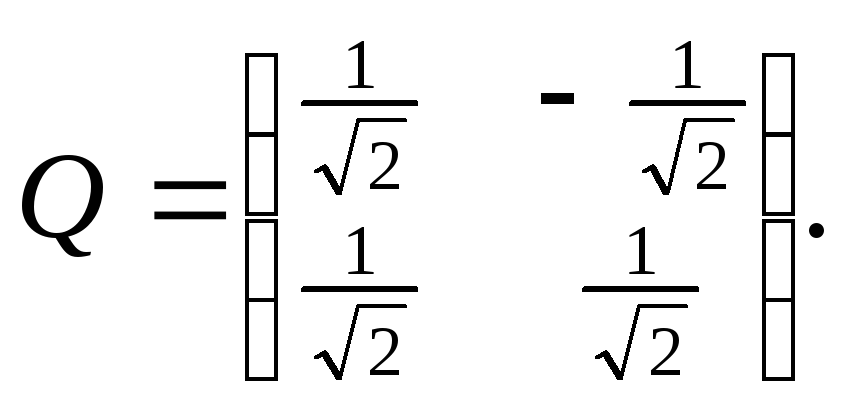
преобразование координат получено.
Заметим,
что в случае ортогональных преобразований
легко получить обратное преобразование
переменных, воспользовавшись свойством
Обратная
матрица равна
Поэтому выполняются соотношения
Ответ.
Канонический
вид
Пример.
Привести квадратичную форму к
каноническому виду и найти ортогональное
преобразование переменных, если
Решение.
Матрица квадратичной формы А=
Характеристическое уравнение
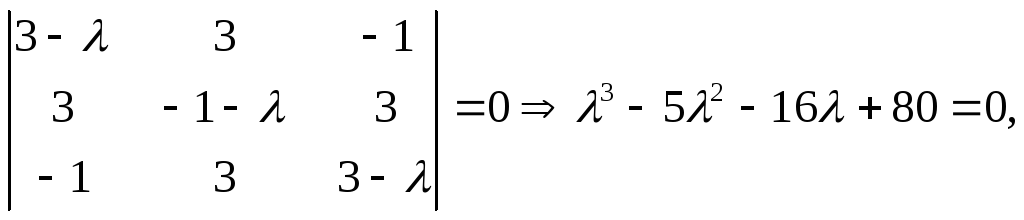
корни
которого λ1=5,
λ2=-4
, λ3=4
Тогда канонический вид квадратичной
формы
Заметим,. что нумерация собственных
значений произвольная. Например, если
взять
то
канонический вид будет
Для каждого такого
варианта обозначений меняется
соответственно расположение (нумерация)
базисных собственных векторов (то есть
система координат), а смысл квадратичной
формы не меняется.
Найдем теперь ортонормированный базис
и преобразование переменных. Составим
систему уравнений:
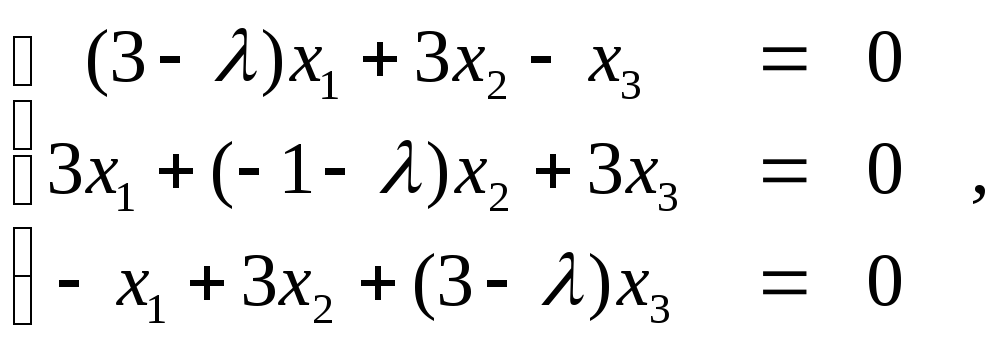
последовательно подставим собственные
значения.
а)
При λ=5 система
примет вид
Выпишем
матрицу системы и подвергнем ее
элементарным преобразованиям:
Получим систему эквивалентную исходной:
Если
х3=k
– любое число, не равное нулю, то множество
собственных векторов (k,k,k).
Пусть k=1,
тогда е1=(1,1,1).
б)
При λ=-4 имеем систему
Преобразуем
матрицу системы
По
последней матрице запишем систему
уравнений
При х3=k,
где k≠0,
множество собственных векторов (k,
-2k,
k).
Возьмем k=1,
тогда е2=(1,
-2, 1).
в)
При λ=4
получим систему уравнений
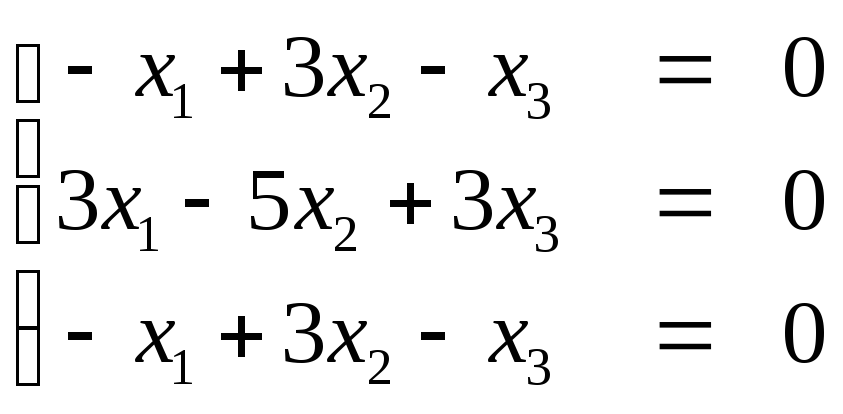
Здесь первое и третье уравнения
одинаковые, поэтому запишем матрицу
системы в виде:
Откуда следует, что
Если х3=k,
где k≠0,
то множество собственных векторов (-k,
0, k).
Пусть k=1,
тогда е3=(-1,0,1).
Получили собственные векторы е1=(1,1,1),
е2=(1,-2,1),
е3=(-1,
0, 1). Легко увидеть, что они попарно
ортогональны. Запишем ортонормированный
базис:
Ортогональная
матрица Q=
Транспонируя
матрицу Q, получим матрицу:
=
И
так как
записываем ортогональное преобразование
переменных
(*)
Ответ.
Квадратичная форма имеет канонический
вид
в базисе из собственных векторов и может
быть получена с помощью преобразования
координат в виде (*).
Отметим
некоторые свойства квадратичных форм:
-
Канонический
вид квадратичной формы не определяется
однозначно, так как зависит от выбора
системы координат (базисных векторов). -
В
каноническом виде число слагаемых с
положительными (отрицательными)
коэффициентами не зависит от способа
приведения формы к каноническому виду. -
Ранг матрицы квадратичной формы не
меняется при линейных преобразованиях
переменных. Ранг всегда равен количеству
ненулевых коэффициентов в канонической
форме. -
Квадратичная форма называется
положительно (отрицательно) определенной,
если при всех значениях переменных, из
которых хотя бы одно отлично от нуля,
выполняется
>0,
<0.
Например,положительно
определенная форма, а
отрицательно определенная.
5. Если все
собственные значения матрицы квадратичной
формы положительны, то
>0
положительно определена. Если все
собственные значения отрицательны, то
<
0- отрицательно определенная форма.
6. Знакоопределенность
квадратичной формы может быть установлена
с помощью критерия Сильвестра: если все
главные миноры матрицы квадратичной
формы положительны, то квадратичная
форма положительно определена. Если
все главные миноры матрицы нечетного
порядка положительны, то квадратичная
форма отрицательно определена.
Продемонстрируем
на примере перечисленные свойства.
Пример.
Дана квадратичная форма
Ее канонический вид
получен с помощью собственных значений
λ1=1 ,λ2=5. Приведем теперь
эту форму к каноническому виду по первому
способу с помощью выделения полных
квадратов.
Таким образом
Канонический вид квадратичной формы
зависит от выбора линейного преобразования
переменных, то есть от выбора системы
координат. Если, например, взять L=1, то
уравнения
являются уравнениями одного и того же
эллипса в разных системах координат.
Пример.
В предыдущем примере мы обратили внимание
на то, что канонический вид квадратичной
формы можно записать разными способами:
Во всех этих записях число слагаемых с
положительными и отрицательными
коэффициентами одно и то же.
Пример. Исследовать на знакоопределенность
квадратичную форму
Решение. Составим матрицу данной
квадратичной формы А=
и вычислим главные угловые миноры
М1=3>0,
М2=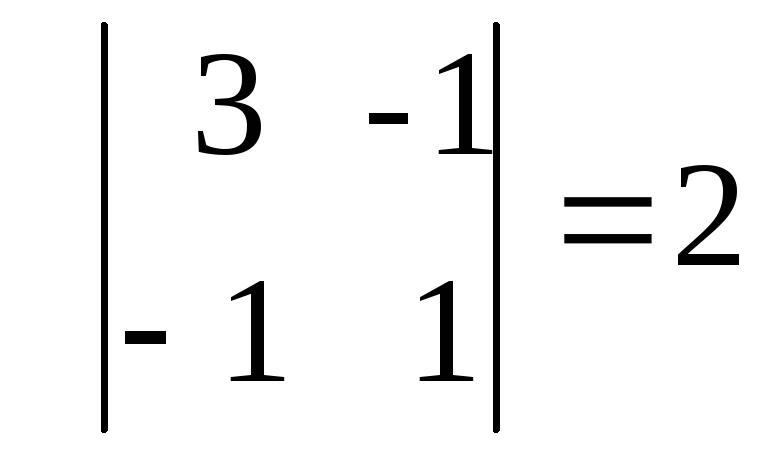
М3=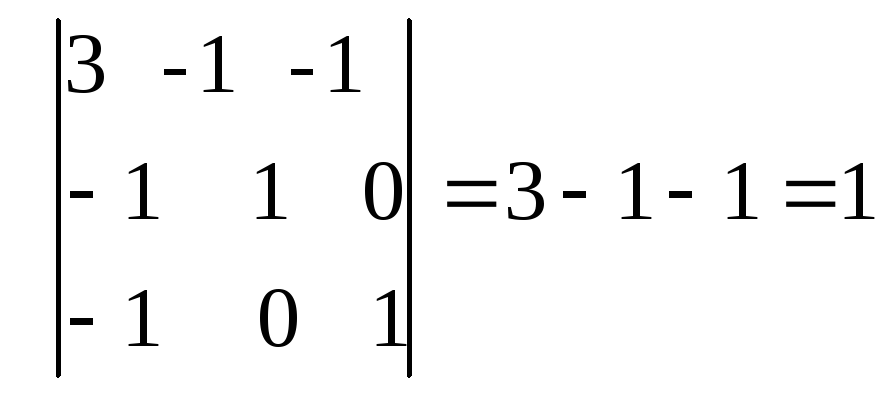
Следовательно,
по критерию Сильвестра квадратичная
форма положительно определенная.
В заключение рассмотрим экономический
смысл понятий собственного значения и
собственного вектора. Предположим, что
на некотором предприятии в начале года
заменяют 20 % оборудования, проработавшего
два года, и все оборудование, проработавшее
три года. То оборудование, которое было
в эксплуатации один год, не заменяется.
Для анализа и прогнозирования экономических
параметров работы предприятия надо
знать устойчивое, т.е. не изменяющееся
из года в год, распределение количества
единиц работающего оборудования. Введем
следующие обозначения:
количество
единиц оборудования, проработавшего i
лет к началу года t, тогда
Это равенство означает, что не заменяется
новое оборудование прошлого года,
заменяется 20 % оборудования, проработавшего
два года к началу предыдущего года и
все оборудование, проработавшее три
года к началу предыдущего года.
Это равенство означает, что два года
проработает то оборудование, которое
к началу предыдущего года эксплуатировалось
один год.
т.е. три года эксплуатируют то оборудование,
которое к началу года проработало два
сезона и не было заменено. Введем матрицы
тогда все
предыдущие рассуждения описываются
уравнением
Если нас интересует устойчивое
распределение, то
и приходится решать уравнение
Если справедливо предположение о том,
что оборудование заменяется пропорционально
количеству единиц техники, находящейся
на предприятии, то приходится искать
распределение, которое является решением
уравнения
Задача отыскания таких λ , при которых
существует ненулевое решение уравнения
и приводит к понятию собственного
вектора и собственного значения
оператора.
Упражнения для
самостоятельного решения
-
Привести
к каноническому виду квадратичную
форму L=х2–у2-4ху
путем выделения полного квадрата. Какую
кривую определяет уравнение L(x,y)=1? -
Привести
к каноническому виду квадратичную
форму, выделяя полные квадраты, L= -
Привести
к каноническому виду квадратичную
форму, определив собственные значения
ее матрицы
Ответы: 1.
2.
3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Квадратичные формы и их определение
- Квадратичные формы
Квадратичные формы и их определение
Определение. Квадратичной формой L (x1, x2, …, xn) от n переменных называется сумма, каждый член которой является или квадратом одной из переменных, или произведением двух различных переменных, взятых с некоторым коэффициентом, то есть

Допускаем, что в квадратичной форме (2.44) aij — действительные числа. Распишем квадратичную форму (2.44), разбив слагаемые, содержащие произведения переменных, на две равные части:
Матрица

или A = {aij} (i, j = 1, 2, …, n) является симметричной, так как aij = aji, называется матрицей квадратичной формы (2.44).
Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма называется невырожденной, если ее матрица невырожденная.
Если 
Выражение XT AX представляет собой квадратичную форму в матричном виде.
Пример 1. Записать в матричном виде квадратичную форму
Решение. Матрица данной квадратичной формы имеет вид
А =
Значит,
Квадратичная форма называется канонической (или другими словами, имеет канонический вид), если все aij = 0, когда i ≠ j. Тогда квадратичная форма будет иметь вид
Рассмотрим следующую теорему.
ТЕОРЕМА 1. Произвольная квадратичная форма приводится к каноническому виду.
Доказательство. Пусть задана квадратичная форма (2.44) с матрицей (2.45) в базисе 
Матрица B является матрицей перехода от базиса

к некоторому базису

Примечание. Действительная квадратная матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна единице и сумма произведений соответствующих элементов из двух разных столбцов равна нулю. Необходимое и достаточное условие ортогональности матрицы В является условие ВT ⋅ B = Е.
Пусть X и Y являются векторами-столбцами из координат вектора 
или

Примечание. При доказательстве данной теоремы использовали транспонирование произведения матриц по формуле (СY)T = YT ⋅ CT.
Заметим, что в канонической форме (2.48) λ1, λ2, …, λn являются собственными числами матрицы A.
Пример 2. Привести квадратичную форму 
Решение. Матрица данной квадратичной формы имеет вид 

Характеристическое уравнение данной системы имеет вид

Решив данное уравнение, находим λ1 = 6, λ2 = 1. Значит канонический вид данной квадратичной формы является 
Найдем ортогональную матрицу.
Столбцами ортогональной матрицы, которая приводит квадратичную форму к каноническому виду, является ортонормированный собственные вектор-столбец матрицы A.
Сначала найдем нормированный собственный вектор-столбец матрицы A с собственным значением λ1 = 6. Для этого из системы (2.49) имеем систему для нахождения координат вектора:
Из данной системы находим x2 = 2x1 или u2 = 2u1. Значит, при произвольном u1, отличном от нуля, столбец 


Аналогично находим вектор-столбец матрицы A с собственным значением λ2 = 1, а именно из системы:
Находим x1 = –2x2 или при произвольном s, отличном от нуля, столбец 

Замечание. Легко проверить, что 
Рассмотрим на примере еще один метод приведения квадратичной формы к каноническому виду.
Метод Лагранжа приведения квадратичной формы к каноническому виду заключается в последовательном выделении полных квадратов.
Пример 3. Привести к каноническому виду квадратичную форму

Итак, невырожденное линейное преобразование
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные разными способами квадратичные формы имеют ряд общих свойств.
Сформулируем одно из этих свойств, которое выражает закон инерции квадратичных форм, и заключается в следующем: все канонические формы, к которым приводится данная квадратичная форма, имеют:
1) одно и то же число нулевых коэффициентов;
2) одно и то же число положительных коэффициентов;
3) одно и то же число отрицательных коэффициентов.
Определение 1. Квадратичная форма L (x1, x2, …, xn) называется положительно определенной, если для всех действительных значений x1, x2, …, xn используется неравенство L (x1, x2, …, xn) > 0.
Определение 2. Если L (x1, x2, …, xn) является положительно определенной формой, то квадратичная формаL (x1, x2, …, xn) < 0 называется отрицательно определенной.
Необходимые и достаточные условия положительной (отрицательной) определенности квадратичной формы дает следующая теорема.
ТЕОРЕМА 2. Для того чтобы квадратичная форма L = XT AX была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения λi (i = 1, 2, …, n) матрицы A были положительными (отрицательными).
Данную теорему приводим без доказательства.
Во многих случаях для установления знакоопределенности квадратичной формы удобно применять критерии Сильвестра.
ТЕОРЕМА 3. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительными, то есть


Следует заметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака “минус” для минора первого порядка.
Например, квадратичная форма L в примере 2 является положительно определенной на основании теоремы 2, так как корни характеристического уравнения λ1 = 6 и λ2 = 1 являются положительными.
Второй способ. Так как главные миноры матрицы A

Квадратичные формы
Однородный многочлен второй степени относительно переменных
называется квадратичной формой от этих переменных. Если взять 
или
где
Выражение (1.28), а следует и квадратичная форма (1.26) полностью определяется матрицей 
Выполняя замену базиса, квадратичную форму (1.26) можно привести к виду:
где 


Выражение (1.29) называется каноническим видом квадратичной формы (1.26).
Рассмотрим квадратичную форму 

Тогда квадратичную форму можно записать так:
Квадратичная форма 



Если 

Решение примеров:
Пример 1.99
Квадратичная форма
положительно определенной.
Квадратичная форма
отрицательно определенная.
Квадратичная форма
неопределенной.
Квадратичная форма
является отрицательно определенной.
Пример 1.100
Используя теорию квадратичных форм, привести к каноническому виду уравнения линии второго порядка
Решение. Уравнение линии запишем в виде 
Сложим характеристическое уравнение матрицы 

Корни уравнения 


Свойства квадратичной формы (1.30) связаны с собственными числами матрицы
Пример 1.101
Привести к каноническому виду уравнения линии 
Решение. Группа старших членов этого уравнения квадратическую форму 
Собственными значениями будут числа 




Лекции:
- Преобразование выражений, содержащих переменную под знаком логарифма
- Метод неопределенных коэффициентов
- Несобственный интеграл первого рода
- Функциональные ряды. Область сходимости. Равномерная сходимость
- Производные тригонометрических функций
- Интегралы, зависящие от параметра
- Умножение логарифмов: пример решения
- Вычислить определитель матрицы
- Геометрический и физический смысл производной
- Найти фундаментальную систему решений
Содержание:
Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.
Понятие квадратичной формы
Квадратичной формой
Пример:
Сумма 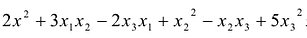
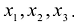
Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при 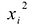
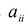
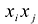
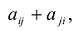
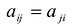
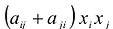
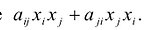
Матрица: 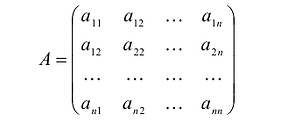
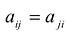
С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.
где А – матрица квадратичной формы, X – матрица-столбец неизвестных:
Приведенные выкладки показывают, в частности, что если А -симметрическая матрица, то выражение 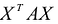
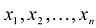
результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид 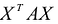
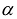
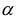
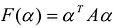
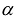
Канонический базис квадратичной формы
Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. 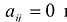
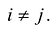
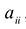
В этом случае матрица квадратичной формы имеет диагональный вид:
Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.
Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.
Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.
Пусть дана квадратичная форма 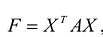
где 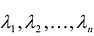
Применим к квадратичной форме линейное преобразование 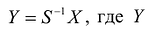
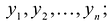
Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.
Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.
Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1 или -1, т.е. квадратичная форма имеет вид:
Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.
Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.
Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.
Эту теорему называют законом инерции квадратичных форм.
Базис 
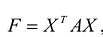
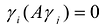
Если 
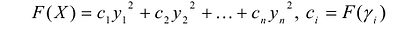


Теорема. Если 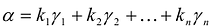

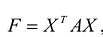
Доказательство:
Эта теорема утверждает, что если известны канонический базис 
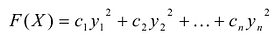
- разложить вектор а по каноническому базису
:
- коэффициенты разложения
подставить вместо неизвестных
в канонический вид квадратичной формы:
Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.
Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.
Канонический базис из собственных векторов матрицы квадратичной формы
Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов 
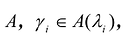
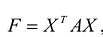
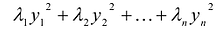

Доказательство:
Канонический базис Якоби квадратичной формы 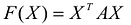
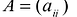
называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что
Обозначим через 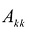
Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. 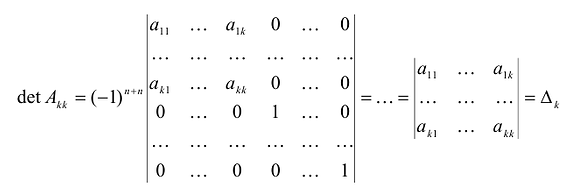
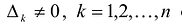
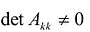
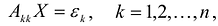
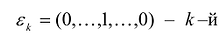
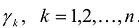
Теорема. матрица А квадратичной формы 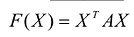

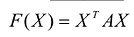


Положительно и отрицательно определенные квадратичные формы
Квадратичная форма F{X) называется положительно определенной, если значение F(X) на каждом ненулевом значении а больше нуля, т.е.:
Если же F(a) < 0 на каждом 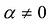
Теорема. Дана квадратичная форма 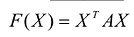

канонический вид 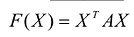

- Квадратичная форма F(X) положительно определена тогда и только тогда, когда
.
- Квадратичная форма F{X) отрицательно определена тогда и только тогда, когда
Доказательство:
Необходимость. Дано, что F(X) – положительно определенная форма. Так как 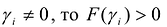
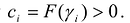
Достаточность. Дано, что в каноническом виде все коэффициенты 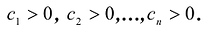

Так как 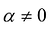
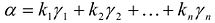
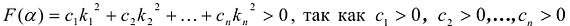
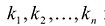
Аналогично доказывается и второе утверждение.
Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.
Теорема. Дана квадратичная форма 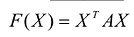
- Квадратичная форма F(X) положительно определена тогда и только тогда, когда все собственные значения матрицы А положительны.
- Квадратичная форма F(X) отрицательно определена тогда и только тогда, когда все собственные значения матрицы А отрицательны.
- Заказать решение задач по высшей математике
Доказательство:
Докажем первое утверждение. Рассмотрим ортонормированный базис 
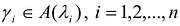
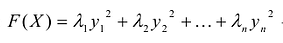

Второе предложение доказывается аналогично.
Лемма. Если какой-нибудь угловой минор 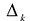
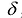
Теорема (Критерий Сильвестра). Справедливы следующие утверждения:
- Квадратичная форма
положительно определена тогда и только тогда, когда главные миноры матрицы А положительны.
- Квадратичная форма
отрицательно определена тогда и только тогда, когда главные миноры матрицы А четного порядка положительны, а главные миноры матрицы А нечетного порядка отрицательны.
Доказательство: Докажем первое утверждение.
Необходимость. Дано, что F(X) положительно определена. Покажем, что все угловые миноры матрицы А отличны от нуля. Допустим обратное, и пусть 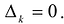
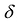
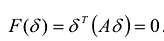
Итак, матрица А удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби 
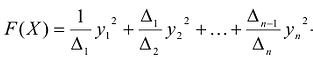

что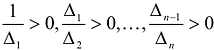
Достаточность. Если 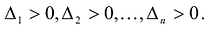
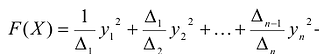
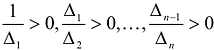
Аналогично доказывается второе утверждение теоремы.
Применение квадратичных форм к исследованию кривых второго прядка
В общем случае кривая второго порядка в базисе 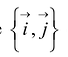
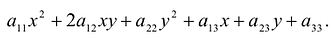
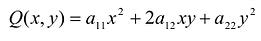
Задача о приведении кривой 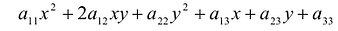
Пусть 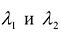
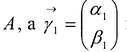
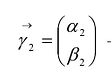
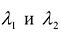
Ортонормированные векторы 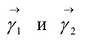
Пусть 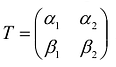
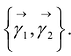
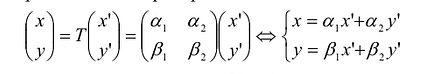
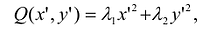
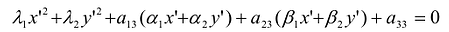
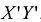
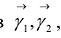
Выделив в этом уравнении полные квадраты, получим 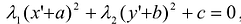
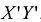
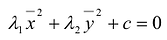
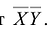
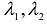
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 сентября 2021 года; проверки требуют 3 правки.
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение[править | править код]
Пусть 



Функция 
если её можно представить в виде
где 


Связанные определения и свойства[править | править код]
.
- где
— матрица квадратичной формы в новом базисе.
- Из формулы
следует, что определитель матрицы квадратичной формы не является её инвариантом (т.е. не сохраняется при замене базиса, в отличие, например, от матрицы линейного отображения), но её ранг — является. Таким образом, определено понятие ранга квадратичной формы.
- Если матрица квадратичной формы имеет полный ранг
, то квадратичную форму называют невырожденной, в противном случае — вырожденной.
- Для любой квадратичной формы
существует единственная симметричная билинейная форма
, такая, что
. Билинейную форму
называют полярной к
, если она может быть вычислена по формуле
- Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
Знакоопределённые и знакопеременные формы[править | править код]
В случае, когда 
Для решения вопроса о том, является ли данная квадратичная форма положительно (отрицательно) определённой, используется критерий Сильвестра:
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
Канонический вид[править | править код]
Вещественный случай[править | править код]
В случае, когда 
где 



Существует также нормальный вид квадратичной формы:

Для приведения квадратичной формы к каноническому виду обычно используются метод Лагранжа или ортогональные преобразования базиса, причем привести данную квадратичную форму к каноническому виду можно не одним, а многими способами.
Число 



Комплексный случай[править | править код]
В случае, когда 
где 
Примеры[править | править код]
См. также[править | править код]
- Теорема Витта
- Метод Лагранжа приведения квадратичной формы к каноническому виду
Примечания[править | править код]
Литература[править | править код]
- Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
- Гельфанд И. М., Линейная алгебра. Курс лекций.
- Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
- Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.
- Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
- Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
- Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.
Линейные и квадратичные формы
Рассмотрим скалярную (числовую) функцию векторного аргумента
, которая каждому значению векторного аргумента
, т.е. каждому числовому столбцу размеров
, ставит в соответствие число (значение скалярной функции). Наиболее простыми функциями векторного аргумента являются многочлены.
Многочленом первой степени от переменных
называется выражение вида
, где числа
— коэффициенты многочлена (предполагается, что среди коэффициентов
есть отличные от нуля); коэффициент
называется свободным членом. Многочлен первой степени называется однородным, если
для любого числа
. Нетрудно показать, что многочлен
будет однородным тогда и только тогда, когда отсутствует свободный член
.
Линейной формой переменных называется однородный многочлен первой степени
(6.3)
где коэффициенты многочлена (6.3) называются коэффициентами линейной формы. Составляя из коэффициентов матрицу-строку
(строка коэффициентов линейной формы), а из переменных — матрицу-столбец
, линейную форму можно записать в виде
(6.4)
Многочленом второй степени от переменных
называется выражение вида
, где числа
— коэффициенты многочлена:
— старшие коэффициенты (или коэффициенты квадратичных членов),
— коэффициенты линейных членов,
— свободный член. У многочлена второй степени не все старшие коэффициенты
равны нулю одновременно. Многочлен второй степени называется однородным, если
. Нетрудно показать, что многочлен
будет однородным тогда и только тогда, когда отсутствуют линейные члены и свободный член
.
Квадратичной формой переменных называется однородный многочлен второй степени
(6.5)
коэффициенты которого удовлетворяют условиям симметричности . Это условие не ограничивает общности, так как сумму двух подобных членов
с неравными коэффициентами
(при
) всегда можно заменить суммой
с равными коэффициентами, положив
. Приводя подобные члены, квадратичную форму (6.5) можно представить в виде
Это вид квадратичной формы с приведенными подобными членами.
Симметрическая матрица , составленная из коэффициентов квадратичной формы (6.5), называется матрицей квадратичной формы. Определитель этой матрицы называется дискриминантом, а ее ранг — рангом квадратичной формы. Квадратичная форма называется вырожденной, если ее матрица вырожденная
, в противном случае, когда матрица невырожденная
, квадратичная форма называется невырожденной.
Составляя из переменных матрицу-столбец , квадратичную форму можно записать в виде
(6.6)
Чтобы получить матрицу квадратичной формы (6.6), нужно:
1) записать квадратичную форму в виде (6.5), разбив удвоенные произведения на сумму двух одинаковых слагаемых;
2) из коэффициентов в (6.5) составить матрицу квадратичной формы. Коэффициенты у отсутствующих членов считаются равными нулю.
Чтобы составить матрицу квадратичной формы с приведенными подобными членами, нужно на главной диагонали матрицы поставить коэффициенты при квадратах переменных, а элементы, симметричные главной диагонали, взять равными половине соответствующих коэффициентов у произведений разных переменных.
Пример 6.4. Составить матрицу квадратичной формы, найти ее дискриминант и ранг:
Решение. Приведем данную квадратичную форму к виду (6.5):
Получили коэффициенты . Следовательно, матрица квадратичной формы имеет вид
Сравнивая эту матрицу с коэффициентами заданной первоначально формы отмечаем, что на главной диагонали стоят коэффициенты при квадратах переменных, а элементы, симметричные относительно главной диагонали, равны половине соответствующих коэффициентов у произведений разных переменных. Вычисляем дискриминант и ранг квадратичной формы
(так как определитель матрицы не равен нулю).
Пример 6.5. Записать линейную и квадратичную формы
a) ;
б)
в матричном виде как функции векторного аргумента и найти их производные первого и второго порядков.
Решение. а) Запишем линейную форму в матричном виде:
где — строка коэффициентов линейной формы. Находим градиент
и матрицу Гессе
, где
— нулевая матрица 3-го порядка.
б) По заданной квадратичной форме с приведенными подобными членами составляем ее матрицу, записывая коэффициенты 1,3,1 при квадратах
переменных на главную диагональ:
, а половины соответствующих коэффициентов при произведениях
— симметрично главной диагонали:
. Коэффициенты у отсутствующих членов
заменяем нулями:
. Получаем матричную форму записи данной квадратичной формы
где — матрица квадратичной формы. Находим градиент функции
и матрицу Гессе
Вычислим дискриминант и ранг данной квадратичной формы: .
Замечания 6.3
1. Важным примером линейной формы служит первый дифференциал скалярной функции векторного аргумента
где дифференциалы являются переменными линейной формы, градиент
, вычисленный при некотором фиксированном значении аргумента, является строкой коэффициентов линейной формы, а дифференциал векторного аргумента
служит столбцом переменных линейной формы.
2. Важным примером квадратичной формы служит второй дифференциал скалярной функции векторного аргумента:
где дифференциалы являются переменными квадратичной формы, матрица Гессе
, вычисленная при некотором фиксированном значении аргумента, является матрицей квадратичной формы, а дифференциал векторного аргумента
служит столбцом переменных квадратичной формы. При этом дискриминант квадратичной формы равен гессиану скалярной функции, вычисленному при некотором значении векторного аргумента
.
3. Как и в случае с многочленами одной переменной многочлены нескольких переменных можно рассматривать либо как функции, применяя к ним понятия математического анализа, либо как алгебраические выражения определенного вида, над которыми можно производить некоторые действия по указанным правилам. Например, линейная форма (6.3) или квадратичная форма (6.5) определены как многочлены, т.е. выражения некоторого вида. При этом можно не указывать область значений переменных, равенство двух многочленов понимать как равенство их степеней и соответствующих коэффициентов и т.п. В то же время, линейную и квадратичную формы можно рассматривать как скалярные функции векторного аргумента. При этом необходимо указывать область определения, равенство двух функций понимать как равенство их значений при каждом значении аргумента и т.п. Каждый из двух подходов полезен для выяснения тех или иных свойств многочленов, и в силу основной теоремы алгебры оба подхода по существу совпадают.
Преобразования форм при линейной замене переменных
Рассмотрим, как меняются коэффициенты линейной и квадратичной форм при линейной замене переменных.
Пусть переменные (условно называемые старыми) заменяются на переменные
(условно называемые новыми) по формулам:
(6.7)
где — некоторые числа
. В формуле (6.7) каждая старая переменная является линейной формой новых переменных. Такая замена переменных называется линейной. Составим из коэффициентов
линейных форм (6.7) квадратную матрицу линейной замены переменных
. Тогда формулы (6.7) можно записать в виде
(6.8)
Линейная замена (6.8) называется невырожденной, если определитель матрицы отличен от нуля.
Свойства линейных невырожденных замен переменных
1. Если — линейная невырожденная замена переменных, то обратная замена
, выражающая новые переменные
через старые
, является также линейной и невырожденной.
2. Если и
— линейные невырожденные замены переменных, то замена
является также линейной и невырожденной.
Получим формулу изменения коэффициентов линейной формы при линейной невырожденной замене переменных. Подставляя выражение (6.8) в линейную форму , получаем снова линейную форму
, коэффициенты
которой связаны с коэффициентами
заданной формы (6.4) равенством
(6.9)
Пример 6.6. Получить формулы преобразования первого дифференциала скалярной функции при линейной невырожденной замене векторного аргумента.
Решение. Пусть — скалярная функция векторного аргумента
. Первый дифференциал
является линейной формой дифференциалов
независимых переменных (см. п. 1 замечаний 6.3).
Рассмотрим сложную функцию , где
— линейная замена векторного аргумента. Учитывая, что матрица Якоби
и
(так как
), найдем первый дифференциал сложной функции
Таким образом, форма первого дифференциала не изменяется при линейной замене аргумента. Это частный случай известного свойства инвариантности формы первого дифференциала.
Получим формулу изменения матрицы квадратичной формы (6.6) при линейной невырожденной замене переменных. Подставляя (6.8) в (6.6), получаем
т.е. квадратичную форму , матрица которой связана с матрицей заданной квадратичной формы равенством
(6.10)
Пример 6.7. Найти второй дифференциал сложной функции , где
, в окрестности некоторого фиксированного значения векторного аргумента
, если известны матрица Гессе, вычисленная при
, и матрица
линейной замены переменных:
Решение. Второй дифференциал скалярной функции
является квадратичной формой дифференциалов независимых переменных (см. п.2 замечаний 6.3), причем матрица Гессе является матрицей этой квадратичной формы. При линейной замене переменных матрица Гессе функции
преобразуется по закону (6.10), т.е.
Следовательно, искомый дифференциал имеет вид
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
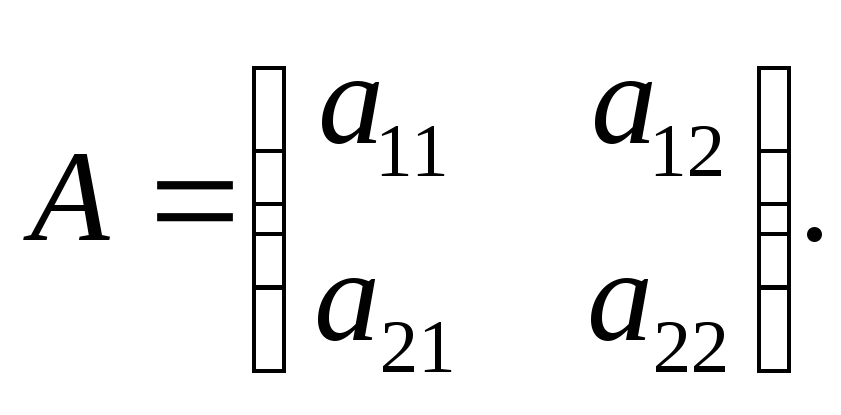
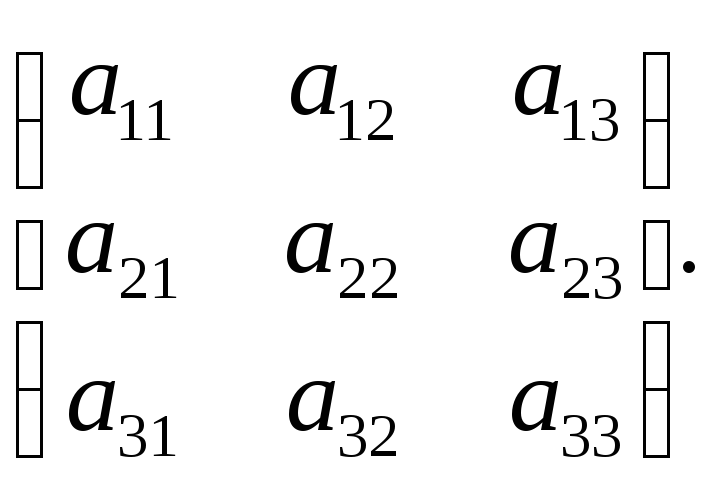
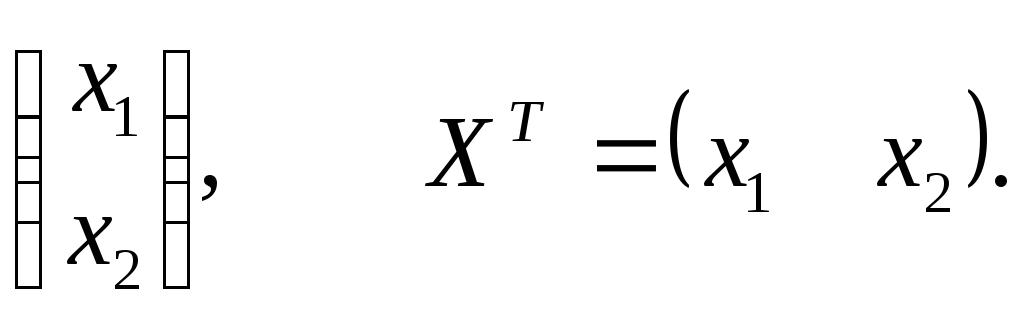
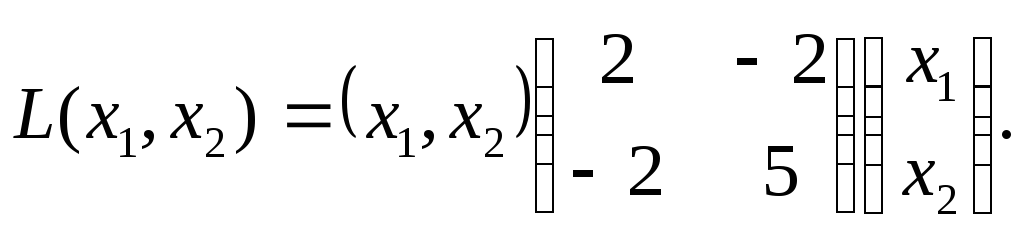
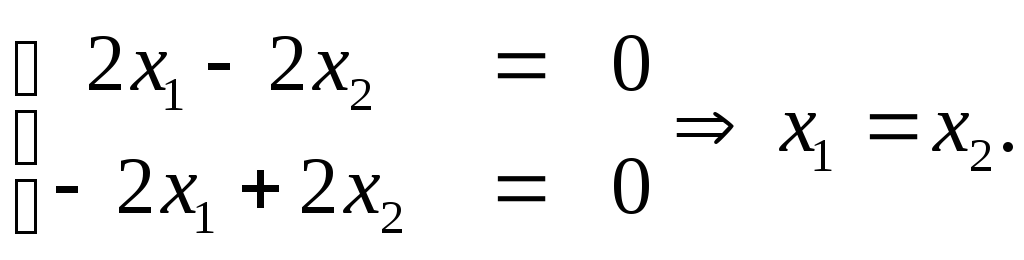
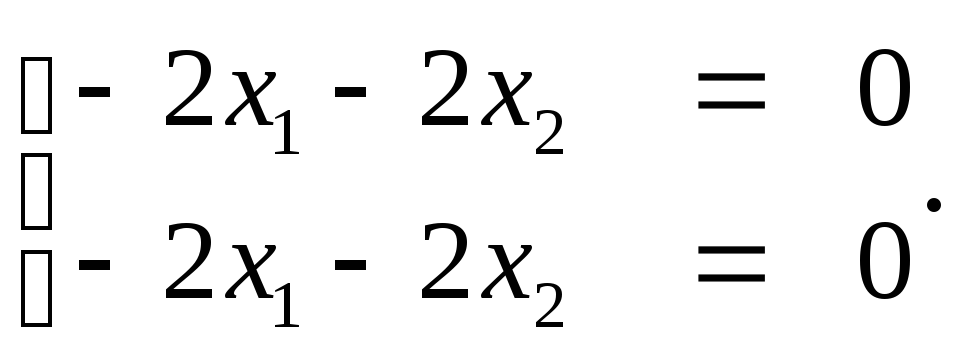
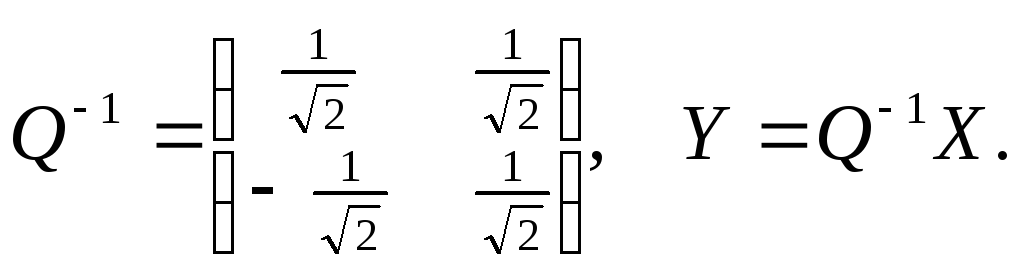
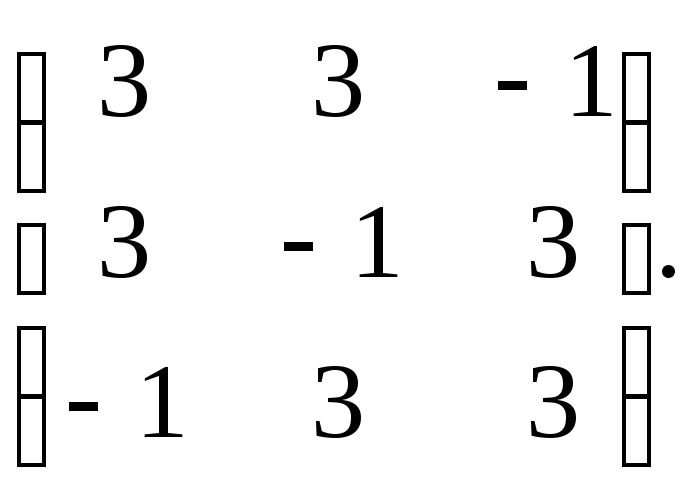
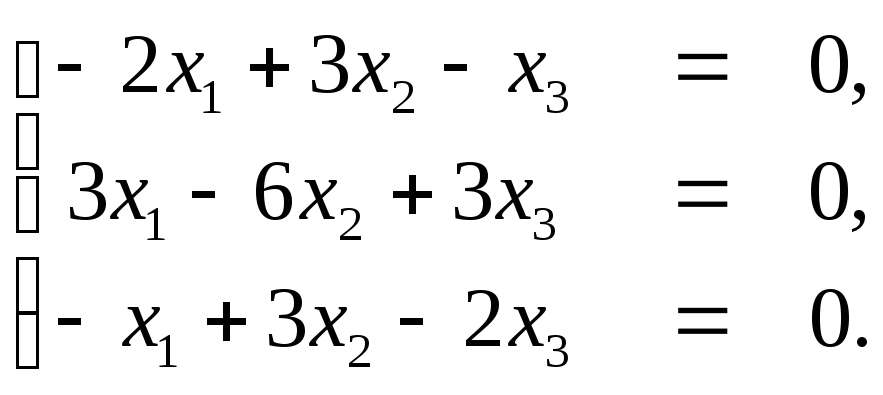
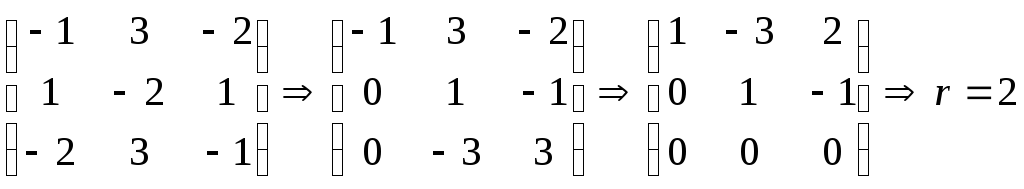
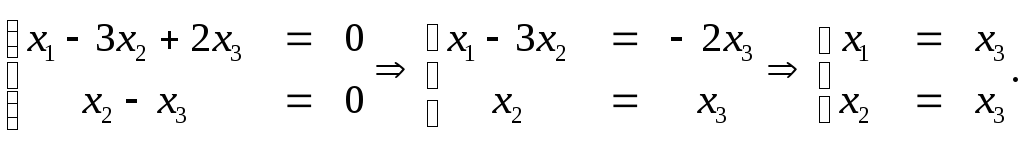
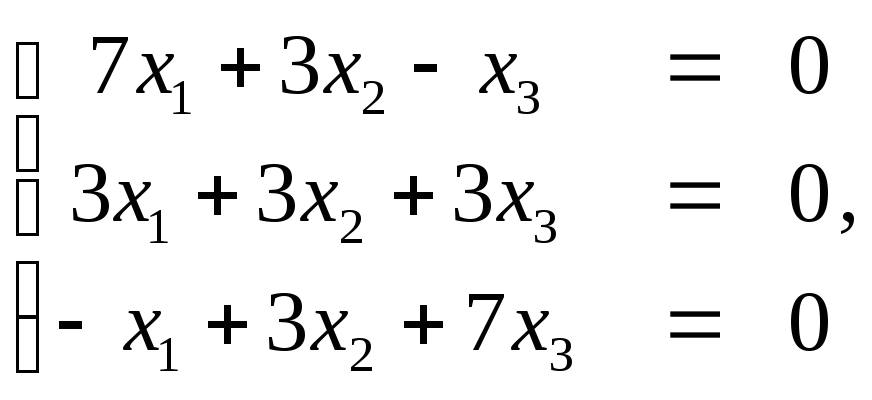
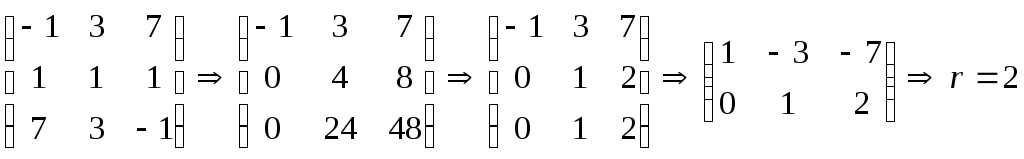

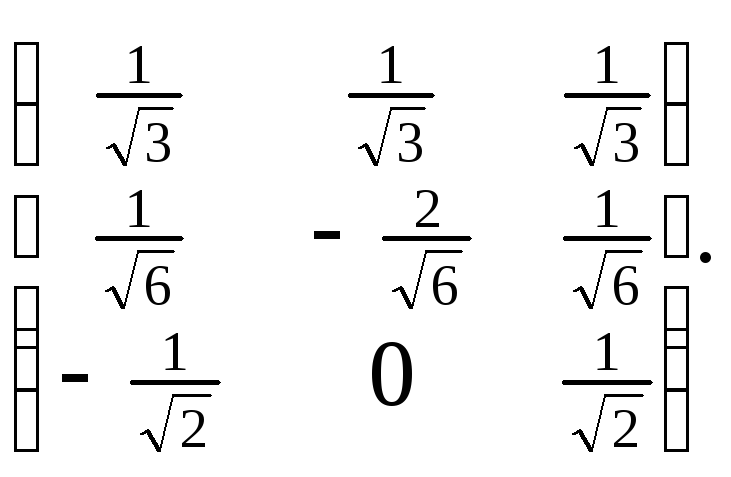
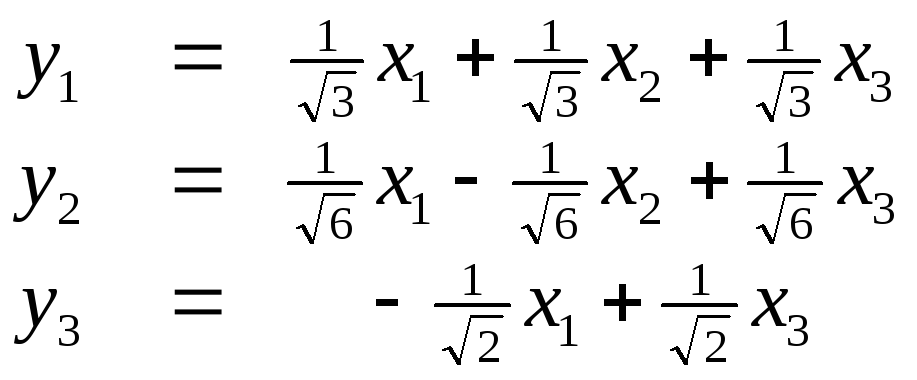
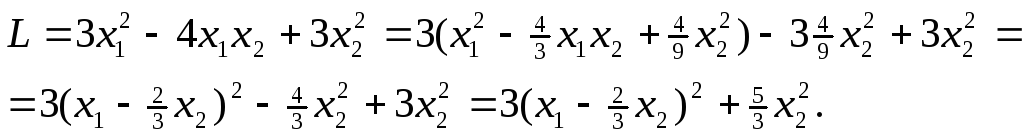

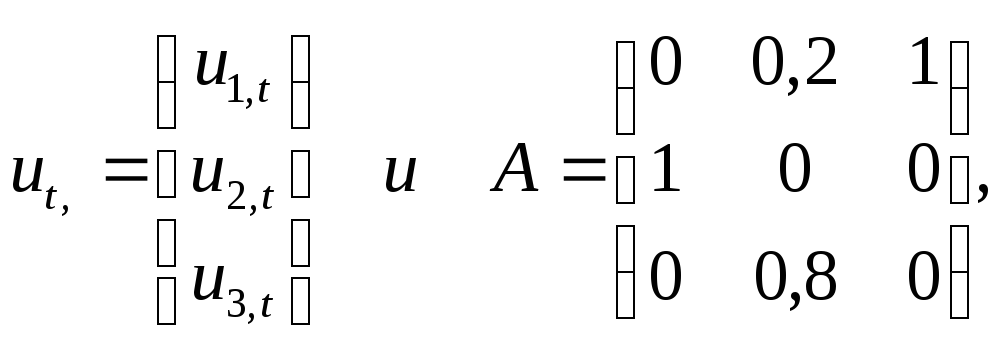


































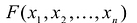
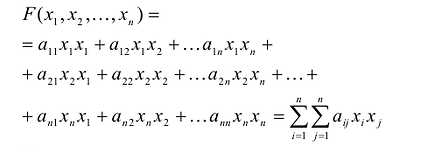
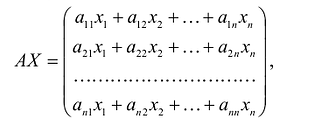
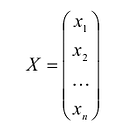
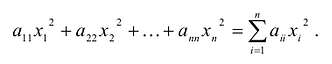

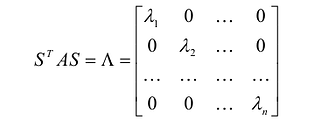
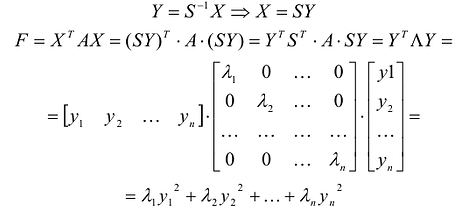
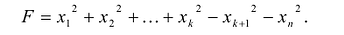
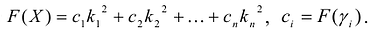
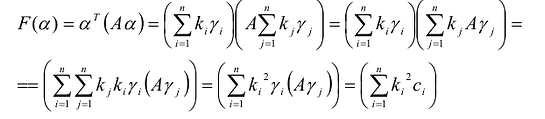
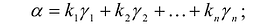
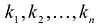 подставить вместо неизвестных
подставить вместо неизвестных 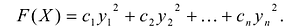
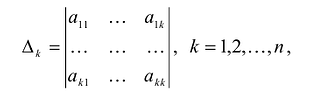
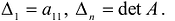

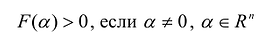
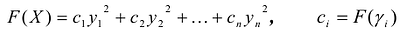
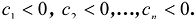
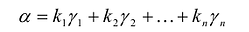
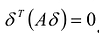
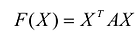 положительно определена тогда и только тогда, когда главные миноры матрицы А положительны.
положительно определена тогда и только тогда, когда главные миноры матрицы А положительны.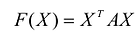 отрицательно определена тогда и только тогда, когда главные миноры матрицы А четного порядка положительны, а главные миноры матрицы А нечетного порядка отрицательны.
отрицательно определена тогда и только тогда, когда главные миноры матрицы А четного порядка положительны, а главные миноры матрицы А нечетного порядка отрицательны.