Как найти матрицу abc

Как найти матрицу abc

Калькулятор матриц – действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Матричный калькулятор

Матрица A
Матрица B

Показатель степени:

Число:

Метод поиска обратной матрицы
Метод Гауса-Жордана
Метод союзной матрицы

Метод решения СЛАУ AX=B
Метод Гауса
Матричный метод
Метод Крамера

Элементарное преобразование

и

Выводить числа в виде

с знаками после запятой

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji

Выполнено действий:

Также может быть интересно:

  • Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
  • Калькулятор комплексных чисел

Как пользоваться калькулятором матриц

  1. Выберите матрицу (или матрицы) с помощью переключателей ()
  2. Укажите размер с помощью выпадающих списков под матрицей ( × )
  3. Заполните элементы (нулевые элементы можно не заполнять.)
  4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
  5. Нажмите кнопку .
  6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2), неправильные дроби () и десятичные дроби (2.4) с указанием числа знаков после запятой.

Ввод данных и функционал

  • В качестве элементов используются обыкновенные правильные дроби (1/2, 29/7, -1/125), десятичные дроби (12, -0.01, 3.14), а также числа в экспоненциальной форме (2.5e3, 1e-2).
  • Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
  • Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
  • Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
  • Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
  • Используйте стрелки (←, ↑, →, ↓) для перемещения по элементам

Что умеет наш калькулятор матриц?

С одной матрицей (только Матрица A или Матрица B)

  • Транспонировать;
  • Вычислять определитель;
  • Находить ранг и след;
  • Возводить в степень;
  • Умножать на число;
  • Вычислять обратную матрицу;
  • Приводить к треугольному и ступенчатому вид;
  • Находить LU-разложение;
  • Выполнять элементарные преобразования;
  • Выполнять действия с выражениями, содержащими матрицы.

С двумя матрицами (Матрица A и Матрица B)

  • Складывать;
  • Вычитать;
  • Умножать;
  • Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
  • Выполнять действия с выражениями, содержащими матрицы.

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

  • Целые и дробные числа
  • Матрицы A, B
  • Знаки арифметических действий: + - * /
  • Круглые скобки для изменения приоритета операций: ( )
  • Транспонирование: ^T
  • Возведение в целую степень: ^

Примеры корректных выражений

  • Cложение двух матриц: A+B, (A)+(B), ((A) + B)
  • Возведение линейной комбинации матриц в степень: (3A - 0.5B)^5
  • Произведение транспонированной матрицы на исходную: A^TA
  • Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.

Примеры матриц

Элементы матрицы

Элементы A обозначаются aij, где i – номер строки, в которой находится элемент, j – номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii

Единичная матрица En×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An

Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц An×m и Bn×m — матрица Cn×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij

Разность матриц An×m и Bn×m — матрица Cn×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij

Умножение матриц An×k и Bk×m — матрица Cn×m, у которой элемент (cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + ... + aik·bkj

Источник

Пример 1:

Заданы матрицы A, B, C. Найти:

a) (3A + 2B)⋅C

б) вычислить определитель матрицы А.

                                      А                                           В                                      С

Решение от преподавателя:

Пример 2:

Даны матрицы А, В и С. Вычислить матрицу D = AB – C:

Решение от преподавателя:

Пример 3:

Заданы матрицы A, B, C. Найти матрицы (если они существуют):

 2A-3B; 5(A+B+E);   A+C;  A∙B;   B∙A;   A∙BT ;  A∙C;   A∙TC;   C∙BT.

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

  • 22423 авторов готовы помочь тебе.
  • 2402 онлайн
Источник

Содержание:

  • Матрицы: основные определения и понятия
  • Умножение матрицы на число
  • Сложение и вычитание матриц
  • Умножение матриц
  • Транспонирование матрицы
  • Минор и алгебраическое дополнение
  • Вычисление определителя
  • Нахождение обратной матрицы
  • Нахождение ранга матрицы

Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.

На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.

Примеры по темам:

  • Матрицы: основные определения и понятия
  • Умножение матрицы на число
  • Сложение и вычитание матриц
  • Умножение матриц
  • Транспонирование матрицы
  • Минор и алгебраическое дополнение
  • Вычисление определителя
  • Нахождение обратной матрицы
  • Нахождение ранга матрицы

Матрицы: основные определения и понятия

Теоретический материал по теме – основные определения и понятия матриц.

Пример

Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?

Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:

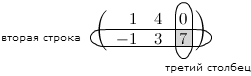
Таким образом, $a_{23}=7$.

Ответ. $a_{23}=7$

Умножение матрицы на число

Теоретический материал по теме – умножение матрицы на число.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.

Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$

Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$

Сложение и вычитание матриц

Теоретический материал по теме – сложение и вычитание матриц.

Пример

Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$

Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$

$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$

Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$

Пример

Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$

Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$

$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$

Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$

Умножение матриц

Теоретический материал по теме – умножение матриц.

Пример

Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$

Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .

Вычисли элементы матрицы $C$ :

$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $

$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $

$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $

$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $

$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $

$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $

Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .

Выполним произведения в более компактном виде:

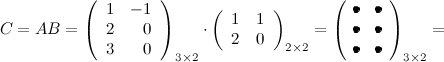
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$

Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .

Транспонирование матрицы

Теоретический материал по теме – транспонирование матрицы.

Пример

Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$

Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$

Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$

Минор и алгебраическое дополнение

Теоретический материал по теме – минор и алгебраическое дополнение.

Пример

Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .

Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

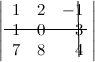
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$

Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$

Пример

Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .

Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$

Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$

Вычисление определителя

Теоретический материал по теме – методы вычисления определителей.

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$

$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:

$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$

$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$

Ответ. $Delta=-80$

Нахождение обратной матрицы

Теоретический материал по теме – нахождение обратной матрицы.

Пример

Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:

$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$

От второй строки отнимаем две первых:

$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$

Первую и вторую строки меняем местами:

$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$

От второй строки отнимаем две первых:

$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$

Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$

Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$

Пример

Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$

Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$

Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$

Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$

Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$

Пример

Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$

Решение. Вычисляем определитель матрицы:

$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$

$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$

Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:

$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$

Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :

$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$

$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$

$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$

$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$

$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$

$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$

$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$

$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$

$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$

Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$

Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$

Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$

Нахождение ранга матрицы

Теоретический материал по теме – нахождение ранга матрицы.

Пример

Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$

Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей – две четвертых:

$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$

Ко второй строке прибавим пять первых, к третьей – три третьих:

$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$

Меняем местами первую и вторую строчки:

$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$

Далее четвертую и первую строки:

$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$

Ответ. $operatorname{rang} A=2$

Пример

Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.

Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:

$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$

так как содержит два пропорциональных столбца (первый и второй); второй минор

$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$

преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:

$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$

И так как первая и вторая строки пропорциональны, то минор равен нулю.

Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$

Ответ. $operatorname{rang} A=2$

Читать первую тему – основные определения и понятия матриц,
раздела матрицы.

Источник
    Виды матриц.

  • Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах
    Матрица
    где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
    Сокращённое обозначение матрицы A=(aij)m×n.
  • Порядок матрицы — это число ее строк или столбцов.
  • Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
  • Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
  • Квадратная матрица — это матрица у которой число строк равно числу столбцов:
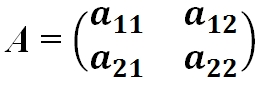
    Квадратная матрица 2х2
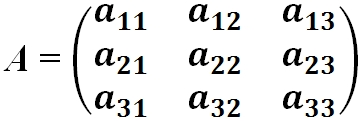
    Квадратная матрица 3х3
  • Матрица-столбец — это матрица, у которой всего один столбец:
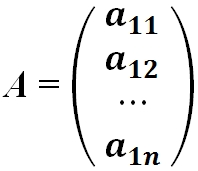
    Матрица-столбец
  • Матрица-строка — это матрица, у которой всего одна строка:
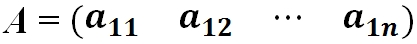
    Матрица-строка
  • Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
  • Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
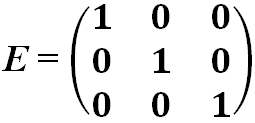
    Единичная матрица
  • Матрица квадратная диагональная:
    Матрица квадратная диагональная
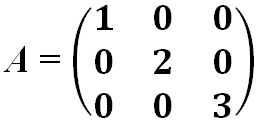
  • Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
  • Матрица верхняя треугольная:Матрица верхняя треугольная
  • Матрица нижняя треугольная:
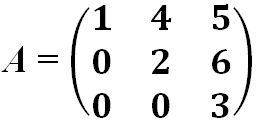
    Матрица нижняя треугольная
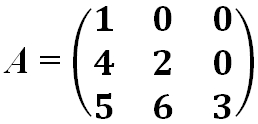
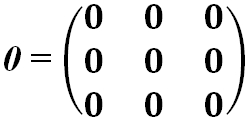
  • Нулевая матрица — это матрица, все элементы которой равны 0:
    Нулевая матрица
    Операции над матрицами.

  • Равенство матриц.
    Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
    то есть при всех i, j aij=bij.
  • Сложение матриц.
    Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1.
  • Умножение матрицы на число.
    Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2.
  • Умножение матриц.
    Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
    cij=ai1b1j+ai2b2j+ … aikbkj.
    Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3.
  • Транспонированные матрицы.
    Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
    Полученная матрица обозначается через A’ или AT. Пример 4.
    Квадратная матрица называется симметричной, если A=A’, то есть для элементов выполнены равенства aij=aji.
  • Обратная матрица.
    Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
    Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:
    A*A^{-1}=A^{-1}*A=E
    Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная A^{-1}={1/{detA}}(A^V)^T, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
    1) (A^{-1})^{-1}=A
    2) {alpha}*A^{-1}={1/{alpha}}*A^{-1}
    3) (A*B)^{-1}=B^{-1}*A^{-1}
    4) (A^{-1})^{T}=(A^{T})^{-1}
  • Алгоритм нахождения А-1 заключается в следующих пунктах:
    1) Находим det A, проверяем det A ≠ 0.
    2) Находим Mij — все миноры матрицы A.
    3) Определяем A_{ij}=(-1)^{i+j}M_{ij}
    4) Строим матрицу алгебраических дополнений A^{V}=(A_{ij}) и транспонируем: (A^{V})^T=(A_{ij})
    5) Делим каждый элемент матрицы на det A: A^{-1}={1/{det A}}(A^V)^T Пример 5.
  • Элементарные преобразования строк (столбцов) матрицы:
    1) перестановка строк (столбцов);
    2) умножение строки (столбца) на число α ≠ 0;
    3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число.
  • Решение матричных уравнений.
    Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
    Простейшие типы матричных уравнений:
    1) A*X=B. Матрица A – квадратная и невырожденная,
    |A| ≠ 0, следовательно, существует обратная матрица A-1.
    Умножим уравнение на A-1 слева: A^{-1}*A*X=A^{-1}*B,~E*X=A^{-1}*B,~X=A^{-1}*B
    2) X*A=B. Матрица A – квадратная, |A| ≠ 0.
    Умножим уравнение на A-1 справа: X*A*A^{-1}=B*A^{-1} {doubleright} X=B*A^{-1}.
    3) A*X*B=C. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
    Умножим уравнение на A-1 слева: A^{-1}*A*X*B=A^{-1}*C~{doubleright}~X*B=A^{-1}*C
    Умножим уравнение на B-1 справа: X*B*B^{-1}=A^{-1}*C*B^{-1}~{doubleright}~X=A^{-1}*C*B^{-1}.
  • Ранг матрицы.
    Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
    Mk этой матрицы: r=r(A)=rang A
    Матрицы называются эквивалентными, что обозначается
    A ∼ B, если r(A)=r(B).
    Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.
  • Метод окаймляющих миноров.
    Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка: M_2 = delim{|}{matrix{2}{2}{{a_{i,j}} {a_{i,j+1}} {a_{i+1,j}} {a_{i+1,j+1}}} }{|}.
    Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
    Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
    Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6.
  • Метод элементарных преобразований.
    Элементарные преобразования матрицы не меняют ее ранга.
    К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
    Для определения ранга матрицы A методом элементарных преобразований следует:
    1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
    2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
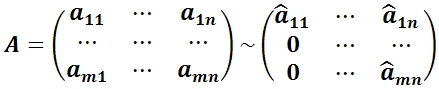
    Рисунок №14 Определение ранга матрицы
    3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
    Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
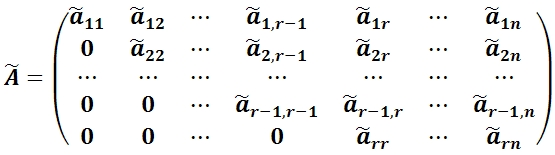
    Рисунок №15 Определение ранга мастера
    Тогда ранг матрицы A равен: rang A = rang Ã.
    Свойства определителей.

  1. Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
  2. При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:
    delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}= - delim{|}{matrix{3}{3}{{a_{21}} {a_{22}} {a_{23}}{a_{11}} {a_{12}} {a_{13}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
  4. Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:
    delim{|}{matrix{3}{3}{{k*a_{11}} {k*a_{12}} {k*a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|} = k*delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|},~k=const
  5. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
    delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {0} {0} {0} {a_{31}} {a_{32}} {a_{33}}} }{|} = 0
  6. Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
  7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
    delim{|}{A}{|}=delim{|}{matrix{3}{3}{{{a{prime}}_{11}+{{a{{prime}{prime}}}_{11}}} {{a{prime}}_{12}+{{a{{prime}{prime}}}_{12}}} {{a{prime}}_{13}+{{a{{prime}{prime}}}_{13}}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}=
    {=}delim{|}{matrix{3}{3}{{{a{prime}}_{11}} {{a{prime}}_{12}} {{a{prime}}_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}+delim{|}{matrix{3}{3}{{{a{prime}{prime}}_{11}} {{a{prime}{prime}}_{12}} {{a{prime}{prime}}_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  8. Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
    delim{|}{matrix{3}{3}{{a_{11}+{k*a_{21}}} {a_{12}+{k*a_{22}}} {a_{13}+{k*a_{23}}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}=delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  9. Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
    delim{|}{A}{|}=delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}={a_{i1}}{A_{i1}}+{a_{i2}}{A_{i2}}+{a_{i3}}{A_{i3}},~i=1,~2,~3
  10. Определитель произведения матриц А и В равен произведению их определителей:
    delim{|}{A*B}{|}=delim{|}{A}{|}*delim{|}{B}{|}.
    Определители n–го порядка.

  • Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
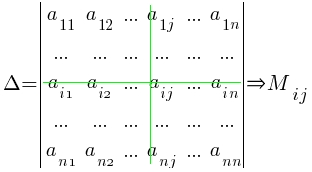
    Минор Мij элемента аij
  • Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
    Для определителей n-го порядка имеют место все перечисленные выше свойства определителей.
  • Правило выбора знака перед минором в алгебраическом дополнении: delim{|}{matrix{3}{3}{{+} {-} {+} {-} {+} {-} {+} {-} {+}} }{|}
  • Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
  • Метод сведения к треугольному виду.
    Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.

Формулы, уравнения, теоремы, примеры решения задач

Источник

mobedouc

mobedouc

Вопрос по алгебре:

Вычислить матрицу D=ABC-3E
(штрихом тут обозначено транспонирование)

Изображение к вопросу

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

degheronve310

degheronve310

Посмотрите предложенное решение; оформление не соблюдалось.

Изображение к ответу

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

  • Отвечать достоверно на те вопросы, на которые знаете
    правильный ответ;
  • Писать подробно, чтобы ответ был исчерпывающий и не
    побуждал на дополнительные вопросы к нему;
  • Писать без грамматических, орфографических и
    пунктуационных ошибок.

Этого делать не стоит:

  • Копировать ответы со сторонних ресурсов. Хорошо ценятся
    уникальные и личные объяснения;
  • Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
    знаю» и так далее;
  • Использовать мат – это неуважительно по отношению к
    пользователям;
  • Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Источник

Добавить комментарий