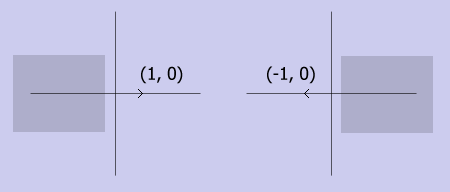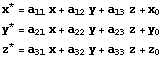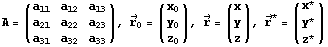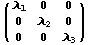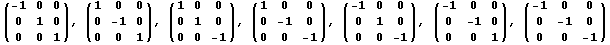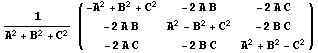Как найти матрицу аффинного преобразования - Сайт, где вы сможете решить свои вопросы

Что за зверь — аффинные преобразования?

Время на прочтение
4 мин

Количество просмотров 38K

Скорее всего, каждый из Вас хоть раз в жизни слышал термин «аффинные преобразования». Действительно, все постоянно о них говорят: «инвариантность к аффинным преобразованиям», «аугментация с помощью аффинных преобразований», «аффинные преобразования в компьютерной графике» и так далее. Однако, далеко не все могут сходу ответить на простой вопрос: «А расскажите, что такое аффинные преобразования простыми словами».

Вы сможете? В любом случае, давайте немного обсудим этот вопрос.

Что такое аффинное преобразование?

Начнем с классики – определение из Википедии.

Аффинное преобразование (от лат. affinis «соприкасающийся, близкий, смежный») — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.

Внесем немного ясности.

Во-первых, что значит «отображение в себя»? Это значит, что если мы находились в пространстве R^n , то после образования мы должны остаться в нем же. Например: если мы применили какое-то преобразование к прямоугольнику и получили параллелепипед, то мы вышли из R^2 в R^3 . А вот если из прямоугольника у нас получился другой прямоугольник, то все хорошо, мы отобразили исходное пространство в себя. Формально это описывается так: «преобразование отображает пространство R^n в R^n ». Если записать с помощью формул: .

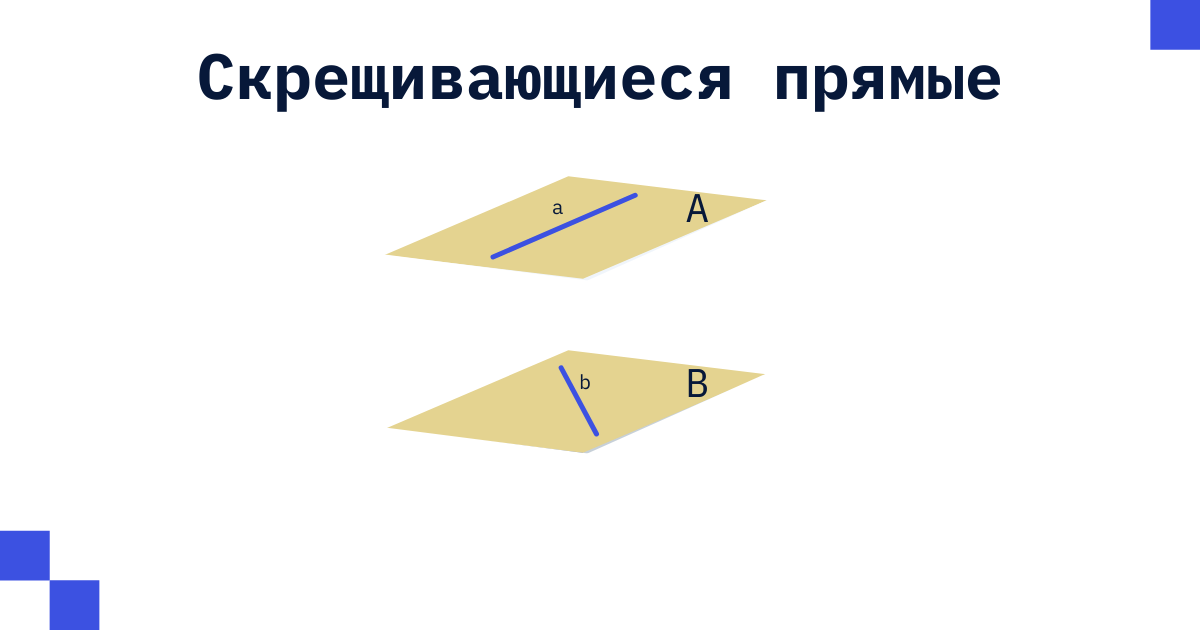
Во-вторых, что такое «скрещивающиеся прямые»? Конечно, все это проходили в школе, но на всякий случай напомним. Прямые называются скрещивающимися, если они не лежат в одной плоскости. Вот если бы они лежали в одной плоскости и пересекались, они назывались бы пересекающимися. А если в разных плоскостях, то скрещивающимися. Пример – на рисунке.

В целом, это определение уже нам что-то говорит и мы начинаем потихоньку рисовать для себя картинку. Как минимум, мы должны остаться в той же плоскости: значит мы представляем себе декартову систему координат. Здесь речь идет о нескольких прямых, так что давайте представим 2 параллельных линии. Из определения мы понимаем, что после преобразования эти линии должны остаться параллельными. Ну что ж, тогда просто сдвигаем их куда-нибудь из исходного местоположения, да и все.

По сути, мы с Вами только что описали один из видов аффинных преобразований – сдвиг.

Но давайте пойдем чуть дальше и дадим еще одно определение (не нами придуманное).

Преобразование плоскости называется аффинным, если оно непрерывно, взаимно однозначно и образом любой прямой является прямая.

Звучит это, пожалуй, чуть сложней и путанней, но дает нам больше конкретной информации, чем предыдущее определение.

Преобразование называется непрерывным, если «близкие точки переходят в близкие». Т.е. иначе – если у нас есть две точки и они находятся рядом, то после преобразования они все равно будут находиться где-то поблизости друг от друга.

Далее – преобразование взаимооднозначно, если разные точки переводятся в разные точки и в каждую точку переводится какая-то точка. Например: если мы отобразили отрезок и он слипся в точку – это не взаимооднозначное преобразование. Из отрезка мы должны получить ровно такой же отрезок, тогда будет взаимооднозначно (если это сработает для всех отрезков, конечно).

Итак, с определениями мы разобрались. Давайте теперь запишем в общем виде, а как выглядит преобразование координат в формульном виде.

Пусть у нас есть исходная система координат. Точка в этой системе характеризуется двумя числами – и . Совершить переход к новым координатам и мы можем с помощью следующей системы:

$begin{cases} x' = alpha x + beta y + lambda \ y' = gamma x + delta y + mu end{cases}$

При этом, числа должны образовывать невырожденную матрицу:

$begin{pmatrix} alpha & beta \ gamma & delta end{pmatrix}$

На всякий случай: матрица называется невырожденной, если ее определитель не равен нулю, т.е.

$begin{vmatrix} alpha & beta \ gamma & delta end{vmatrix} neq 0$

Можно записать и в более общем в виде.

Аффинное преобразование – преобразование вида , где – обратимая матрица, а . В данном случае, само собой, -мерный вектор.

Примеры аффинных преобразований

Мы с Вами достаточно подробно разобрали, что такое аффинное преобразование и как его можно описать с помощью формул. Давайте теперь рассмотрим популярные примеры.

Приходят ли Вам в голову какие-нибудь претенденты на роль? Позвольте мы внесем свои предложения.

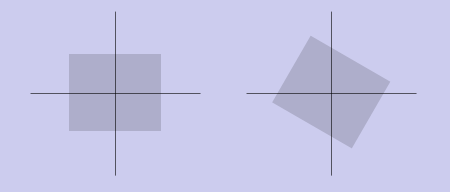
Поворот

Пусть .

Значит, матрица примет вид:

$begin{pmatrix} cos(alpha) & sin(alpha) \ -sin(alpha) & cos(alpha) end{pmatrix}$

И новые координаты будут выглядеть так:

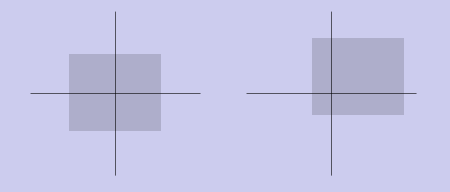
$begin{cases} x' = xcosalpha + y sinalpha \ y' = -xsinalpha + y cosalpha end{cases}$

Ничего не напоминает? Если Вы еще не узнали, то встречайте – это просто повернутая система координат на угол alpha . Т.е. мы применили аффинное преобразование и наша система координат повернулась. Пример этого Вы можете видеть на графике.

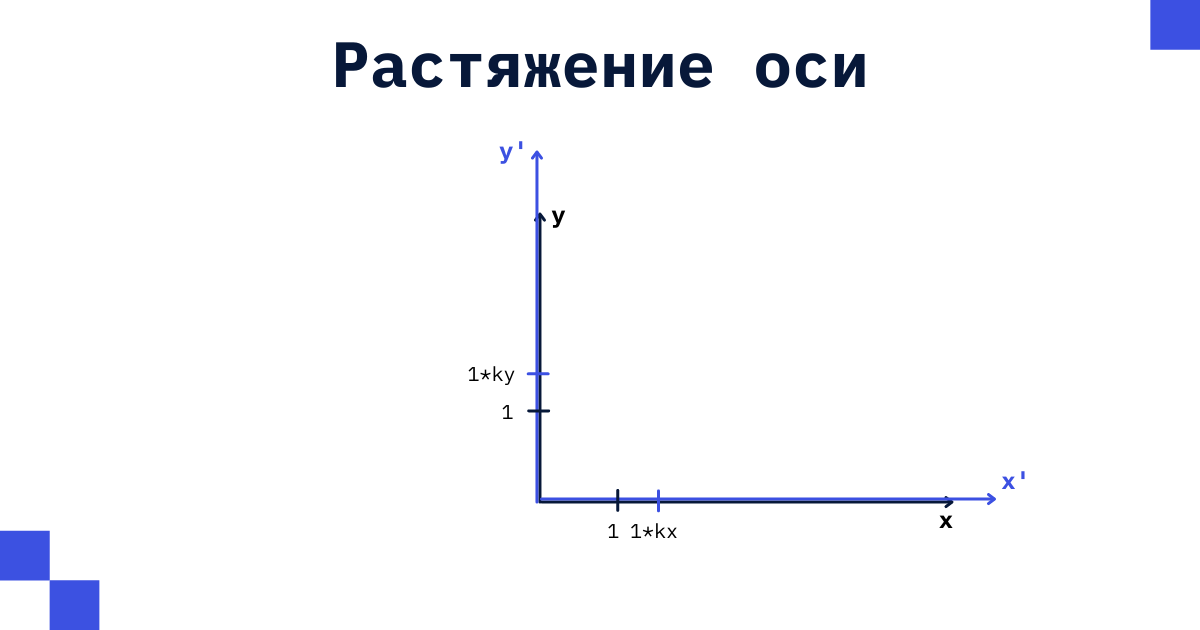
Растяжение-сжатие

Теперь мы предлагаем сконструировать матрицунесколько иначе:

$begin{pmatrix} 1/k_x & 0 \ 0 & 1/k_y end{pmatrix}$

Новые координаты тогда принимают вид:

$begin{cases} x' = x/k_x \ y' = y/k_y end{cases}$

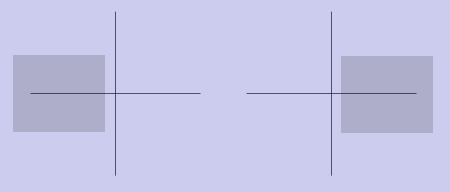
В целом, тут даже уже из вида системы уравнений понятно, что мы просто растягиваем наши оси, если коэффициент меньше 1 и сжимаем, если больше 1. Пример на рисунке.

Кстати говоря, а попробуйте поставить вместо k_x число -1, а вместо k_y просто 1. Что получится? Правильно, мы просто отразим нашу систему координат относительно оси .

Сдвиг

Ну и давайте напоследок еще один пример.

Пусть теперь матрица никак не меняет исходные координаты (т.е. ). А вот lambda пусть равняется -dx , а .

Таким образом, наша система принимает вид:

$begin{cases} x' = x - dx \ y' = y - dy end{cases}$

Если отразить это на графике, то мы просто сдвинули начало координат в точку . Вот, собственно, и вся премудрость.

Эпилог

Эта короткая статья позволит Вам чуть сильней прочувствовать «внутренности» аффинных преобразований (мы надеемся на это). После прочтения попробуйте все-таки ответить на вопрос, который мы ставили в самом начале – «А расскажите, что такое аффинные преобразования простыми словами». Теперь сможете?

P.S. Кстати говоря, было бы неплохо не верить нам на слово и проверить самим – а матрицы , которые мы использовали – точно невырожденные? Может мы вообще что-то противозаконное сделали?…

Источник

Аффинные преобразования на плоскости используются в машинной графике повсеместно. Придумал их Эйлер в 18 веке, развил Мёбиус в 19-ом, в 20-м они переместились в графический адаптер и теперь являются неотъемлемой частью нашей с вами жизни…

Аффинное преобразование — это изменение единичной матрицы с учетом матриц масштабирования, перемещения, сдвига и поворота (ниже, в разделе «Ссылки по теме» есть пункт об этих матрицах).

Не смотря на простоту метода, с его применением возникают какие-то сложности, связанные, видимо, с непониманием, почему именно такие матрицы, почему важен порядок, почему это должно работать.

Хотя, как мне кажется, больше отпугивает само понятие матрицы. Давайте рассмотрим, почему матрицы имеют такие коэффициенты и как это все работает.

Ссылки по теме

Как повернуть изображение. GDI, GDI+, Direct2D, JavaScript
Вращение прямоугольника вокруг произвольной точки
Границы повернутого прямоугольника
Матрицы аффинных преобразований на плоскости

Поворот

Предположим, стоит задача повернуть прямоугольник на некоторый угол относительно его центра. Очевидно, надо рассчитать 4 угловые точки и построить по ним полигон.

Рис.1. Поворот точки Р1 на угол β

Имеем некий прямоугольник с вершинами в точках P1, P2, P3, P4. Рассмотрим точку P1(x,y). Она отстоит от оси абсцисс на угол α. Повернем ее на угол β. Очевидно, что вращение происходит по окружности с центром, находящимся в центре заданного прямоугольника O(x,y).

Рассчитаем координаты новой точки P1′( x′, y′).

Где R – радиус окружности на которой расположена точка P1, и равен (O, P1). Воспользуемся формулами сложения углов (1.1 и 2.1) из справочника:

или

Рис.2. Координаты точки P1 через угол α

Замечаем, что R × cos(α) это не что иное, как координата X точки P1, а R × sin(α) – координата Y. Таким образом, формулы расчета координат новой точки P1′ приобретают вид:

Чтобы выйти на правильную позицию на холсте, прибавим к полученным значениям координаты центра прямоугольника:

И мы только что получили матрицу поворота аффинного преобразования.

Рис.3. Поворот прямоугольника на угол β относительно его центра

В общем виде формулы можно записать как:

В матричном виде:

Где: M11, M12, M21, M22, Dx, Dy – коэффициенты, определяющие преобразование.

Теперь представим себе, что прямоугольник – это на самом деле бесконечная плоскость. И к каждой точке этой плоскости применены одна и те же формула трансформации. Вот это и будет называться аффинным преобразованием на плоскости.

Таким образом, матрицей поворота будет следующая:

Немного кода:

type

TxPoint = packed record

X : single;

Y : single;

end;

//*******************************************************************

// Посчитать координаты точки повернутой на Angle радиан

//*******************************************************************

function CalcAnglePoint(const ACenter, APoint: TxPoint;

const Angle: Single): TxPoint;

var

sn,cs: single;

begin

SinCos(Angle, sn, cs);

Result.X := (APoint.X–ACenter.X) * cs – (APoint.Y–ACenter.Y) * sn +

ACenter.X;

Result.Y := (APoint.X–ACenter.X) * sn + (APoint.Y–ACenter.Y) * cs +

ACenter.Y;

end;

Сдвиг

Еще одно интересное преобразование. Состоит из вертикального сдвига, когда меняется только координата Y, и горизонтального, когда меняется только X.

Для определения величин сдвигов будем использовать углы отклонения от горизонтали или вертикали, т.к. это наиболее часто встречающаяся ситуация.

Снова рассматриваем прямоугольник, помня, что это на самом деле плоскость.

Рис.4. Плоскость с центром трансформации в левой нижней точке P3

Для наглядности деформация будет происходить относительно левой нижней точки P3.

Вначале деформируем следующим образом:

Рис.5. Вертикальный сдвиг

При вертикальном сдвиге координаты X не меняются. Изменяются координаты Y. В данном случае координата Y точки P1 изменилась на расстояние (P2,P2′).

Из чего получим формулу преобразования для Y:

Рис.6. Вертикальный + горизонтальный сдвиги

Теперь добавим горизонтальный сдвиг. Координата X точки P1 изменилась на расстояние (P4,P4′), которое рассчитывается аналогичным образом.

В итоге, формулы для трансформации сдвига выглядят следующим образом:

Или матрицей:

В позиции M12 находится коэффициент, на который нужно умножить расстояние X, чтобы получить величину вертикального смещения по Y. Аналогично, в позиции М21 находится коэффициент, на который умножается расстояние Y для определения горизонтального сдвига. Это на тот случай, если не нужны углы и заранее знаем, на какие величины хотим деформировать.

Немного кода:

//*******************************************************************

// Посчитать координаты точки при сдвиге с углами A и B

//*******************************************************************

function CalcShearPoint(const ACenter, APoint: TxPoint;

const A,B: single): TxPoint;

var

tA, tB: single;

begin

tA := Tan(A);

tB := Tan(B);

Result.X := (APoint.X – ACenter.X) + (APoint.Y – ACenter.Y)*tB +

ACenter.X;

Result.Y := (APoint.X – ACenter.X)*tA + (APoint.Y – ACenter.Y) +

ACenter.Y;

end;

Перемещение и масштабирование

Это очень простые матрицы и в свете всего вышесказанного, думаю, понятные и останавливаться на них особого смысла нет. Поэтому, для полноты картины, просто приведу.

Пермещение	Масштабирование

Композиция

Давайте сейчас воспринимать композицию, как перемножение матриц в порядке слева направо. На самом деле порядок может быть и обратным — когда матрицы домножаются в начало матричного выражения. Об особенностях порядка перемножения рассказано тут.

Предположим, у нас есть следующее преобразование:

На которое следом идет такое преобразование:

Раскроем скобки и преобразуем:

или

где

Это ничто иное, как перемножение матриц коэффициентов:

Соответственно, расчет новых координат выглядит как:

Понятно, что можно умножить получившуюся матрицу на матрицу третьего преобразования, четвертого и т.д. Таким образом, чтобы получить коэффициенты сложного аффинного преобразования, нужно перемножить матрицы коэффициентов в порядке применения трансформаций.

Утверждение, прямо скажем, смелое, но правильное.

Проверим. Допустим, я хочу вначале применить деформацию, а потом повернуть на угол.

Рис.7. Деформация без поворота

На рисунке 7 пока только деформация. Теперь к деформированному прямоугольнику (плоскости) применяю поворот на 80 градусов.

Рис.8. Деформация + поворот

Расчет координат в точности воспроизводит приведенные выше выкладки:

type

T4Point = array [0..3] of TxPoint;

T4Matrix = array [0..3] of Single;

//*******************************************************************

// Комбинированный расчет деформации и поворота

//*******************************************************************

function CalcComboPoints (const APoints: T4Point;

const ACenter: TxPoint; const Angle, A, B: single;

var M: T4Matrix): T4Point;

var

A0,B0,C0,D0: Single; // матрица деформации М0

A1,B1,C1,D1: Single; // матрица поворота М1

A2,B2,C2,D2: Single; // матрица M0 * М1

sn, cs: Single; // синус косинус Angle

tA, tB: Single; // тангенсы углов A, B

i: Integer;

begin

SinCos(Angle,sn,cs);

tA := Tan(A);

tB := Tan(B);

// Деформация

A0 := 1; B0 := tB; C0 := tA; D0 := 1;

// Поворот

A1 := cs; B1 := –sn; C1 :=sn; D1 :=cs;

// Перемножение матриц M0 * M1

A2 := A0 * A1 + C0 * B1;

B2 := B0 * A1 + D0 * B1;

C2 := A0 * C1 + C0 * D1;

D2 := B0 * C1 + D0 * D1;

M[0] := A2; M[1] := B2; M[2] := C2; M[3] := D2;

// Расчет

for i := 0 to Length(APoints)–1 do

begin

Result[i].X := A2*(APoints[i].X – ACenter.X) +

B2*(APoints[i].Y – ACenter.Y) + ACenter.X;

Result[i].Y := C2*(APoints[i].X – ACenter.X) +

D2*(APoints[i].Y – ACenter.Y) + ACenter.Y;

end;

Применение

Аффинные преобразования изменяют геометрию плоскости, при этом сохраняя параллельность линий и соотношение расстояний.

Безусловно, это один из основных методов обработки изображений. Аффинные преобразования используются для исправления искажений и деформаций, возникающих при не самых идеальных ракурсах камеры. Широко используется в машинном обучении и компьютерном зрении.

Лично мне чаще всего попадались проблемы, которые обобщенно можно выразить двумя вопросами:

как повернуть изображение?
как нарисовать эллипс под углом?

Эти два вопроса объединяет одно. Изображение – набор точек, эллипс — геометрическое место точек. Решая вопрос в лоб, надо к каждой точке применить функции поворота. И если для изображения – ну, может быть, то к эллипсу, как фигуре векторной графики, это выглядит топорней некуда.

Аффинное преобразование – это преобразование плоскости. Применяя к плоскости некую трансформацию, мы понимаем, что эта трансформация применяется к каждой точке плоскости. Чтобы плоскость не содержала, это вытянется, сожмется, деформируется, повернется вместе с плоскостью.

Центр трансформации

Все что мы делали ранее, происходило относительно либо центра прямоугольника, либо одной из его вершин. Это центр трансформации. По сути – это начало координат той координатной системы, в которой происходит трансформация. Поэтому, перед всеми преобразованиями необходимо установить центр системы координат.

В Windows этим занимается функция:

function SetViewportOrgEx(DC: HDC; X, Y: Integer;

Point: PPoint): BOOL;

С этой функцией обычно идет еще набор функций, типа изменения окна вывода. Сейчас пока это все не нужно. После применения этой функции начало координат из верхнего левого угла переместиться в указанную точку. Все геометрические построения должны это учитывать. Поэтому лучше изначально писать код так, чтобы все рисовки были в относительных координатах.

Аффинное преобразование Windows

В основе работы с аффинным преобразованием лежит изменение матрицы с учетом масштабирования, перемещения, деформации или поворота. В Windows GDI за матрицу отвечает класс TXForm.

tagXFORM = record

eM11: Single;

eM12: Single;

eM21: Single;

eM22: Single;

eDx: Single;

eDy: Single;

end;

TXForm = tagXFORM;

Знакомые обозначения. Поля имеют смысл ровно тот, который описан и в справочнике, и выше в статье. Это коэффициенты матрицы преобразования.

Необходимо проинициализировать поля записи и применить преобразование функцией Windows GDI:

function SetWorldTransform(DC: HDC; const p2: TXForm): BOOL;

Однако, работать с мировыми координатами и аффинными преобразованиями в Windows GDI — удовольствие так себе. Поэтому рекомендуется это делать в GDI+.

В GDI+ есть масса вариантов, сильно облегчающих жизнь при трансформации плоскости. Но сейчас в плане статьи стоит задача работать именно через матрицы преобразования, поэтому работаем следующим образом.

Необходимо создать экземпляр класса TGPMatrix. Затем проинициализировать его методом:

function TGPMatrix.SetElements(m11, m12, m21, m22, dx, dy: Single): TStatus;

Снова знакомые имена аргументов. Аргументы имеют тот же смысл, что и поля записи TXForm.

После инициализации применяем трансформацию методом TGPGraphics:

function TGPGraphics.SetTransform(matrix: TGPMatrix): TStatus;

После этих манипуляций рисуем все, что хотим нарисовать, не заботясь о расчетах, углах и синусах.

Представим, что один человек рисует портрет, а второй стоит сбоку и смотрит на холст. Для него портрет выглядит деформированным, а для художника, который смотрит прямо, портрет вполне себе правильный, не трансформированный и пока нравится. Что-то похожее происходит при аффинных преобразованиях. Правда, в приведенном примере трансформация перспективная. Но сути дела это не меняет.

Рекомендован следующий порядок при работе с аффинными преобразованиями:

Назначение нового центра координат (спорное утверждение)
Инициализация матрицы преобразования
Применение матрицы
Рисуем эллипс

Композиция

Как выше говорилось, при сложном преобразовании, состоящим из нескольких трансформаций, необходимо перемножить матрицы в порядке применения преобразований. За это отвечает функция Windows GDI:

function CombineTransform(var p1: TXForm; const p2, p3: TXForm): BOOL;

Здесь p2 и p3 — первая и вторая структуры TXForm, результат их комбинирования будет находиться в параметре p1. Т.е. надо понимать, что p3 – это преобразование, накладываемое на p2, т.е. идущее следом за ним. Порядок применения матриц очень важен.

Практика

Весь исходный код можно скачать по ссылке ниже. Чтобы не загромождать буду фрагментировать. Если приводить весь код в статье, до конца можно никогда не добраться.

Перед вызовом этой функции точка начала координат уже установлена в центр прямоугольника.

//****************************************************************

// Рисование с использованием аффинных преобразований

//****************************************************************

procedure TFmRRMain.DrawAffine(const ACanvas: TxIPCanvas;

const ARect: TxRect; const ACenter: TxPoint);

var

val: TxRect; // отображаемый прямоугольник

pnt: TxPoint; // центр вселенной

mode: Integer; // текущий режим отображения

Mx: TGPMatrix; // матрица GDI+ (аналог TXForm)

RotaMx: TXForm; // матрица поворота

SkewMx: TXForm; // матрица сдвига

sn,cs: Single; // синус и косинус угла поворота

tA,tB: Single; // тангенсы углов сдвига

begin

mode := GetCurrMode;

if mode < 9 then exit;

SinCos(–FAngle, sn, cs);

tA := tan(FAngleA);

tB := tan(FAngleB);

Mx := TGPMatrix.Create;

try

with ACanvas do

begin

// прямоугольник фигуры

val := ARect;

// установили центр трансформации

pnt := xPoint(0,0);

// рисуем координатные оси

DrawCoordSystem(ACanvas, val, pnt);

// рисуем исходный прямоугольник

DrawRectPoints(ACanvas, val, True, False, clBtnShadow);

// матрица поворота

RotaMx.eM11 := cs; RotaMx.eM12 := sn;

RotaMx.eM21 := –sn; RotaMx.eM22 := cs;

RotaMx.eDx := 0; RotaMx.eDy := 0;

// матрица сдвига

SkewMx.eM11 := 1; SkewMx.eM12 := tA;

SkewMx.eM21 := tB; SkewMx.eM22 := 1;

SkewMx.eDx := 0; SkewMx.eDy := 0;

// композиция матриц

if mode in [11] then

CombineTransform(RotaMx, SkewMx, RotaMx);

// если поворот, либо сдвиг + поворот

if mode in [9,11] then

MX.SetElements(RotaMx.eM11, RotaMx.eM12,

RotaMx.eM21, RotaMx.eM22, RotaMx.eDx, RotaMx.eDy);

// если сдвиг

if mode in [10] then

MX.SetElements(SkewMx.eM11, SkewMx.eM12,

SkewMx.eM21, SkewMx.eM22, SkewMx.eDx, SkewMx.eDy);

// Установить преобразование

GPGraphics.SetTransform(MX);

// Если есть галка – рисуем кота

if chbAffineImage.Checked then

StretchDraw(GPRectF(val), FImage);

// Если есть галка – рисуем эллипс

if chbAffineEllipse.Checked then

DrawEllipse(ACanvas, val);

// рисуем трансформированный прямоугольник

DrawRectPoints(ACanvas, val, True, True, clIP76Color);

// сбросили все трансформации

GPGraphics.ResetTransform;

end;

finally

FreeAndNil(MX);

end;

Аффинный поворот

Итак, у нас есть демонстрационной приложение, написанное для статьи. Внизу есть ряд кнопок 1..15. Это разные режимы демонстрации. Режимы 9..11 отвечают за демонстрацию аффинных преобразований с предварительным назначением нового центра координат . В режиме 9 видим такую картину:

Рис.9. «Спокойное» аффинное преобразование

Ну, это мы уже видели. Однако, если повернуть прямоугольник, за вершину P1 или в поле «Rotate Angle» увидим интересное изменение:

Рис.10. Подписи к вершинам тоже под углом

Помимо поворота непосредственно прямоугольника, повернулись и подписи вершин.

Преобразование применятся к плоскости, к каждой точке плоскости. Грубо говоря, преобразование применяется ко всему, что на плоскости.

Поэтому, можно предположить, что такой же фокус пройдет и с эллипсом:

Рис.11. Эллипс под углом

То же самое касается и изображения:

Рис.12. Изображение под углом

В чем, собственно, прелесть аффинных преобразований и состоит. Не надо считать каждую точку, писать километры кода. Мы просто рисуем, как будто и нет никаких преобразований, все также прямоугольно, параллельно и перпендикулярно. Все расчеты берет на себя плоскость, к которой применили преобразование.

Фрагмент из вышеприведенного кода:

// Если есть галка – рисуем кота

if chbAffineImage.Checked then

StretchDraw(GPRectF(val),FImage);

// Если есть галка – рисуем эллипс

if chbAffineEllipse.Checked then

DrawEllipse(ACanvas, val);

В функции DrawEllipse нет ничего особенного, вынесена, чтобы не загромождать код:

//******************************************************************

// Просто нарисовать “толстый” синий эллипс

//******************************************************************

procedure DrawEllipse(const ACanvas: TxIPCanvas; const ARect: TxRect);

begin

with Acanvas do

begin

Pen.Color := Darker(clIP76Color,30);

Pen.Width := 3;

Brush.Style := bsClear;

Ellipse(GPRectF(ARect));

Pen.Width := 1;

end;

Т.е. не взирая на все требуемые повороты, деформации и прочие издевательства, спокойно рисуем все в том же прямоугольнике val, все теми же обычными методами.

Аффинный сдвиг

Аналогичные чудеса в режиме деформации сдвига (кнопка 10):

Рис.13. Поперечная деформация (сдвиг) кота

Перед рисованием инициализируем матрицы TXForm и в зависимости, от того что требуется, применяем ту или иную матрицу. Фрагмент из кода выше:

// матрица поворота

RotaMx.eM11 := cs; RotaMx.eM12 := sn;

RotaMx.eM21 := –sn; RotaMx.eM22 := cs;

RotaMx.eDx := 0; RotaMx.eDy := 0;

// матрица сдвига

SkewMx.eM11 := 1; SkewMx.eM12 := tA;

SkewMx.eM21 := tB; SkewMx.eM22 := 1;

SkewMx.eDx := 0; SkewMx.eDy := 0;

// композиция матриц

if mode in [11] then

CombineTransform(RotaMx, SkewMx, RotaMx);

// если поворот, либо сдвиг + поворот

if mode in [9,11] then

MX.SetElements(RotaMx.eM11, RotaMx.eM12,

RotaMx.eM21, RotaMx.eM22, RotaMx.eDx, RotaMx.eDy);

// если сдвиг

if mode in [10] then

MX.SetElements(SkewMx.eM11, SkewMx.eM12,

SkewMx.eM21, SkewMx.eM22, SkewMx.eDx, SkewMx.eDy);

// Установить преобразование

GPGraphics.SetTransform(MX);

Аффинная композиция

В коде выше присутствует композиция матриц — CombineTransform. Последовательность преобразований такая — вначале деформация, потом поворот. Проинспектируем кнопкой 11.

Рис.14. Деформированный, повернутый, замученный кот

Сравним с деформацией на рис.8. Там мы делали композицию матриц руками (в интерфейсе – режим 8), теперь этим занимается Windows GDI.

Рис.15. Все правильно делаем

Перед вызовом функции DrawAffine, необходимо перевести центр системы координат в центр прямоугольника. Напомню, начало системы координат – это центр трансформации. Именно вокруг него вертится вселенная.

try

// находим прямоугольник пропорциональный картинке

val := xRect(0,0,FImage.Width,FImage.Height);

val := GetProportRect(val, rct.Width * (FRect.Right–FRect.Left),

rct.Height * (FRect.Bottom–FRect.Top));

// смещаем его, согласно настройкам FRect

xOffsetRect(val, rct.Width*FRect.Left,rct.Height*FRect.Top);

// находим центр прямоугольника – центр трансформации

pnt := CenterRect(val);

// работаем с аффинным преобразованием

// устанавливаем центр прямоугольника как начало координат

if mode in [9,10,11] then

SetViewportOrgEx(bmp.Canvas.Handle,

Trunc(pnt.X), Trunc(pnt.Y), nil);

with cnv do

begin

...

rct := ClipRect;

// Если центр посредине, надо сместить пространство

if mode in [9,10,11] then

OffsetRect(rct, –Trunc(pnt.X), –Trunc(pnt.y));

...

// Инициализация точек для мыши

FZeroPoint := CalcAnglePoint (pnt,

xPoint(val.Right, val.Top), –FAngle);

FPointA := CalcShearPoint(pnt,

xPoint(val.Right, val.Bottom),FAngleA,FAngleB);

FPointB := CalcShearPoint(pnt,

xPoint(val.Left, val.Top), FAngleA, FAngleB);

FCenterPoint := pnt;

if mode in [10,13] then

// Режим, когда прямоугольник по центру и таскаем за p2 и p4

FPointС := CalcShearPoint(pnt,

xPoint(val.Left, val.Bottom),FAngleA, FAngleB)

else

// Во всех остальных случаях, опорная точка – центр

FPointС := FCenterPoint;

if mode in [9,10,11] then

// при аффинных преобразованиях со смещенным центром

// сдвигаем прямоугольник вывода

xOffsetRect(val, –Trunc(pnt.X), –Trunc(pnt.y));

FCurrRect := val;

...

if mode in [9,10,11] then

DrawAffine(cnv, FCurrRect, FCenterPoint)

...

end;

finally

pbx.Canvas.Draw(0,0,bmp);

FreeAndNil(cnv);

FreeAndNil(bmp);

UpdateMenu;

end;

Это фрагмент обработчика OnPaint того PaintBox, на котором рисуем . Вначале идет вызов SetViewportOrgEx, что переводит начало координат в центр прямоугольника. Потом происходит коррекция прямоугольника области рисования OffsetRect(rct, -Trunc(pnt.X), -Trunc(pnt.y)), иначе все координаты «уплывут» вправо на величину (pnt.x, pnt.y), затем вызов DrawAffine.

Если б мышь знала… Координаты вершин

В приложении есть возможность таскать за некоторые вершины. Тут возникает проблема. Если применяем аффинное преобразование, координаты точек, за которые можно «ухватиться» сильно отличаются от координат в «нормальном» состоянии координатной системы. Поэтому, перед тем как плоскость начнет изменяться, необходимо рассчитать нужные точки, т.е. координаты, понятные мышке.

// Инициализация точек для мыши

FZeroPoint := CalcAnglePoint (pnt,

xPoint(val.Right, val.Top), –FAngle);

FPointA := CalcShearPoint(pnt,

xPoint(val.Right, val.Bottom),FAngleA,FAngleB);

FPointB := CalcShearPoint(pnt,

xPoint(val.Left, val.Top), FAngleA, FAngleB);

FCenterPoint := pnt;

if mode in [10,13] then

// Режим, когда прямоугольник по центру и таскаем за p2 и p4

FPointС := CalcShearPoint(pnt,

xPoint(val.Left, val.Bottom),FAngleA, FAngleB)

else

// Во всех остальных случаях, опорная точка – центр

FPointС := FCenterPoint;

И только потом

xOffsetRect(val, –Trunc(pnt.X), –Trunc(pnt.y));

И только после этого

DrawAffine(cnv, FCurrRect, FCenterPoint)

Функции расчета достались в наследство от предыдущих этапов, когда экспериментировали над прямоугольником без применения аффинных преобразования. Не зря ж в конечном счете экспериментировали.

Конечно, можно сформировать и скомбинировать матрицы, взять коэффициенты и посчитать по формуле. Почти как в CalcComboPoints.

В GDI+ в TGPMatrix для этих целей существуют методы:

function TGPMatrix.TransformPoints(pts: PGPPointF;

count: Integer = 1): TStatus;

function TGPMatrix.TransformPoints(pts: PGPPoint;

count: Integer = 1): TStatus;

Здесь они не используются. Потом как-нибудь обязательно вернемся к ним.

Смещать ли начало координат?

Теоретически рекомендуется делать именно так, смещать и потом трансформировать. И, возможно, это правильно. Но можно обойтись и без этого. Просто привычней работать в «обычной» системе координат, когда точка (0,0) системы находится в левом верхнем углу.

По сути, как это делается, мы уже рассмотрели в самом начале статьи, когда вращали прямоугольник, считали координаты вершин и смещали в нужное место. Давайте это сделаем с помощью аффинных преобразований.

Порядок действий таков:

Определяемся с прямоугольником, в котором что-то хотим нарисовать
Определяемся с центром трансформации (pnt), т.е. точкой, вокруг которой будет происходить трансформация
Смещаем прямоугольник на -pnt.x, -pnt.y, тем самым совмещая центр трансформации с началом координат
Формируем матрицу трансформации
Добавляем матрицу перемещения с параметрами (или просто инициализируем в текущей матрице) eDx=pnt.x, eDy=pnt.y
Рисуем в получившемся смещенном прямоугольнике

//******************************************************************

// Нарисовать прямоугольник под углом, без перевода начала координат

// Если указано, рисовать AImage или эллипс

//******************************************************************

procedure DrawRectAffineRotate(const ACanvas: TxIPCanvas;

const ARect: TxRect; const ACenter: TxPoint; const Angle: Single;

const ADrawEllipse, ADrawPicture: Boolean;

const AImage: TGPImage = nil);

var

MX: TGPMatrix; // матрица преобразования

rct: TxRect; // прямоугольник вывода

sn, cs: Single; // синус косинус заданного угла

begin

SinCos(Angle, sn, cs);

Mx := TGPMatrix.Create;

rct := ARect;

try

with ACanvas do

begin

// сместим прямоугольник, чтобы его центр совпал с началом

xOffsetRect(rct, –ACenter.X, –ACenter.Y);

// инициализация преобразования

MX.SetElements(cs, sn, –sn, cs, ACenter.x, ACenter.y);

// Установить преобразование

GPGraphics.SetTransform(MX);

// Если указано – рисуем изображение

if ADrawPicture and Assigned(AImage) then

StretchDraw(GPRectF(rct), AImage);

// Если указано – рисуем эллипс

if ADrawEllipse then

DrawEllipse(ACanvas, rct);

end;

finally

FreeAndNil(MX);

end;

Сильно сократил код за счет того, что не использую TXForm, а инициализирую сразу TGPMatrix. Что тут изменилось. В матрицу поворота добавил еще смещение в точку (ACenter.x, ACenter.y) – центр прямоугольника, или центр трансформации. Перед рисованием сместил прямоугольник отрисовки так, чтобы он оказался центрирован по началу координат, т.е. точки (0,0). Аффинное преобразование отработает поворот и сместиться на указанные величины по x и y.

Т.е. произойдет ровно тоже самое, что мы делали руками, когда прибавляли координаты центра к расчетным значениям вершин.

В демонстрационном примере это режимы 12..14, которые визуально будут совпадать с 9..11, с той лишь разницей, что перевода центра координат не происходит.

Чтобы продемонстрировать, работоспособность метода, существует последний режим – 15. Помимо основного прямоугольника, рисуется звезда и текст под углом, обратным текущему. Текст в дополнение к повороту также подвергается масштабированию.

Рис.16. Аффинные преобразования в любой требуемой точке плоскости

Я грозился вернуться к теме поворота звезд. Говорил, что есть более правильные методы. Брутальная звезда имени Стетхама, помните? Так вот, наиболее правильным будет вращать звезды, и не только, через аффинное преобразование.

Процедура, отвечающая за рисовку всего этого хозяйства:

procedure TFmRRMain.DrawAffineStars(const ACanvas: TxIPCanvas;

const ARect: TxRect; const ACenter: TxPoint);

var

val: TxRect; // отображаемый прямоугольник

pnt: TxPoint; // центр вселенной

begin

with ACanvas do

begin

// центр координат для прямоугольника

val := ARect;

pnt := ACenter;

// рисуем координатные оси

DrawCoordSystem(ACanvas, val, pnt);

// рисуем исходный прямоугольник с точками

DrawRectPoints(ACanvas, val, True, False, clBtnShadow);

// Рисуем основной прямоугольник (картинка, эллипс)

DrawRectAffineRotate(ACanvas, val, pnt, –FAngle,

chbAffineEllipse.Checked, chbAffineImage.Checked,

FImage.GPImage);

// сместить прямоугольник на начало сист.координат

xOffsetRect(val, –pnt.X, –pnt.Y);

// рисуем описывающий прямоугольник

DrawRectPoints(ACanvas, val, True, True, clIP76Color);

// прямоугольник под звезду

val := ARect;

xOffsetRect(val, ARect.Right – 90, 0);

val.Top := ClipRect.Top + 10;

val.Right := ClipRect.Right;

val.Bottom := ARect.Top + xHeightRect(ARect) / 2;

// Рисуем звезду

DrawStarAffineRotate(ACanvas, val, FAngle, FStarImage.GPImage);

// прямоугольник под текст

xOffsetRect(val, 0, xHeightRect(val)+10);

val.Bottom := ClipRect.Bottom–10;

// Рисуем текст

DrawTextAffineRotate(ACanvas, val, FAngle * 1.5,

abs(FAngle/(2*pi)) + 0.6);

// сбросили все трансформации

GPGraphics.ResetTransform;

end;

Как видно, не очень много, и в принципе, просто.

Процедура для рисовки текста, чуть посложнее. Добавил к повороту еще и преобразование масштаба.

//******************************************************************

// Нарисовать текст под углом, без перевода начала координат

//******************************************************************

procedure DrawTextAffineRotate(const ACanvas: TxIPCanvas;

const ARect: TxRect; const Angle, Scale: Single);

const

ROTA_TEXT = ‘Affine’+#13#10+‘Transformation 2D’+#13#10+‘IP76.RU’;

var

MX: TGPMatrix; // матрица преобразования

MXS: TGPMatrix; // матрица преобразования – масштаб

rct: TxRect; // прямоугольник вывода

pnt: TxPoint; // центр

sn, cs: Single; // синус косинус заданного угла

begin

SinCos(Angle, sn, cs);

MX := TGPMatrix.Create;

MXS := TGPMatrix.Create;

rct := ARect;

pnt := CenterRect(rct);

try

// инициализация вращения

MX.SetElements(cs, sn, –sn, cs, pnt.x,pnt.y);

// инициализация масштаба

MXS.SetElements(Scale, 0, 0, Scale, 0, 0);

// добавить вращение после масштаба

MXS.Multiply(MX, MatrixOrderAppend);

with ACanvas do

begin

// инициализация шрифта

Font.Size := 18;

Font.Style := [fsBold];

Font.Color := clIP76Color;

IPFont.RenderingHint := trhAntiAlias;

IPFont.Alignment := taCenter;

// сбросили все трансформации

GPGraphics.ResetTransform;

// Установить преобразование

GPGraphics.SetTransform(MXS);

// посчитаем прямоугольник вывода для текста

rct.Left := –TextWidth(ROTA_TEXT) / 2;

rct.Top := –TextHeight(ROTA_TEXT) / 2;

rct.Right := rct.Left + TextWidth(ROTA_TEXT) + 2;

rct.Bottom := rct.Top + TextHeight(ROTA_TEXT);

// инициализируем кисть

Brush.Style := bsClear;

// рисуем текст

TextRect(GPRectF(rct), ROTA_TEXT);

end;

finally

FreeAndNil(MX);

FreeAndNil(MXS);

end;

Как видим, матрицы TXForm не используются. Чтобы добавить преобразование в GDI+ используется метод TGPMatrix:

function TGPMatrix.Multiply(matrix: TGPMatrix;

order: TMatrixOrder = MatrixOrderPrepend): TStatus;

Суть такая же, как CombineTransform для Windows GDI. В листинге вначале происходит масштаб, потом поворот.

Видео + скачать

На этом пока все.

Друзья, спасибо за внимание!

Подписывайтесь на телеграм-канал.

Оцените мой труд, жду ваших комментариев.

Скачать (1 036 Кб): Исходники (Delphi XE 7-10)

Скачать (1 843 Кб): Исполняемый файл

Скачать (4 205 Кб): Affine2D

Небольшой комментарий к Affine2D. Если подвести курсор к верхнему правому углу поля отрисовки, появится знак меню. Нажмите его и настройте надписи, картинки, и т.д., по своему усмотрению.

Источник

Аффинные преобразования координат

Рассмотрим аффинное преобразование системы координат в пространстве.

Пусть в пространстве заданы две системы координат $Ovec{e}_1vec{e}_2vec{e}_3$ и $Ovec{e},'_1vec{e},'_2vec{e},'_3$ . Первую систему координат будем условно называть “старой”, а вторую — “новой”. Тогда базис $vec{e}_1,vec{e}_2,vec{e}_3$ — “старый”, а базис $vec{e},'_1,vec{e},'_2,vec{e},'_3$ — “новый”. Старый и новый базисы представим в виде символических матриц-строк: $(vec{e})=begin{pmatrix}vec{e}_1&vec{e}_2&vec{e}_3end{pmatrix}$ , $(vec{e},')=begin{pmatrix}vec{e},'_1&vec{e},'_2&vec{e},'_3end{pmatrix}$ . Поставим следующие задачи:

1) нахождения координат вектора в новом базисе по координатам того же вектора в старом базисе;

2) нахождения координат точки в новой системе координат по координатам той же точки в старой системе координат.

Преобразование координат вектора при замене базиса

Пусть известны координаты векторов нового базиса относительно старого базиса:

$left{!begin{aligned} vec{e},'_1&= s_{11}cdotvec{e}_1+ s_{21}cdotvec{e}_2+s_{31}cdotvec{e}_3,\[2pt] vec{e},'_2&= s_{12}cdotvec{e}_1+ s_{22}cdotvec{e}_2+ s_{32}cdotvec{e}_3,\[2pt]vec{e},'_3&= s_{13}cdotvec{e}_1+ s_{23}cdotvec{e}_2+ s_{33}cdotvec{e}_3. end{aligned}right.$

(2.1)

Записывая по столбцам координаты векторов $vec{e},'_1,vec{e},'_2,vec{e},'_3$ относительно базиса $vec{e}_1,vec{e}_2,vec{e}_3$ , составляем матрицу:

$mathop{S}limits_{(vec{e})to(vec{e},')}= begin{pmatrix} s_{11}& s_{12}& s_{13}\[2pt] s_{21}& s_{22}& s_{23}\[2pt] s_{31}& s_{32}& s_{33} end{pmatrix}.$

(2.2)

Квадратная матрица $mathop{S}limits_{(vec{e})to(vec{e},')}$ , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому (матрицей преобразования базиса).

При помощи матрицы перехода (2.2) формулы (2.1) можно записать в виде:

$begin{pmatrix} vec{e},'_1& vec{e},'_2& vec{e},'_3 end{pmatrix}= begin{pmatrix} vec{e}_1& vec{e}_2& vec{e}_3 end{pmatrix}cdot mathop{S}limits_{(vec{e})to(vec{e},')}quad Leftrightarrowquad (vec{e},')=(vec{e})cdot mathop{S}limits_{(vec{e})to(vec{e},')}.$

(2.3)

Умножение символической матрицы-строки (vec{e}) на матрицу перехода $mathop{S}limits_{(vec{e})to(vec{e},')}$ в (2.3) производится по правилам умножения матриц (см. разд.П.3).

Пусть в базисе (vec{e}) вектор vec{v} имеет координаты v_1,v_2,v_3 , а в базисе (vec{e},') — координаты v'_1,v'_2,v'_3 , т.е.

$vec{v}=v_1cdotvec{e}_1+v_2cdotvec{e}_2+v_3cdotvec{e}_3=v'_1cdotvec{e},'_1+v'_2cdotvec{e},'_2+v'_3cdotvec{e},'_3$ или, короче, $vec{v}=(vec{e})mathop{v}limits_{(vec{e})}=(vec{e},')mathop{v'}limits_{(vec{e},')},$

где $mathop{v}limits_{(vec{e})}=begin{pmatrix}v_1&v_2&v_3end{pmatrix}^T,~mathop{v'}limits_{(vec{e},')}=begin{pmatrix}v'_1&v'_2&v'_3end{pmatrix}^T$ — координатные столбцы вектора vec{v} .

Подставляя в правую часть последнего равенства выражение (2.3), получаем $vec{v}=(vec{e})mathop{v}limits_{(vec{e})}=(vec{e})mathop{S}limits_{(vec{e})to(vec{e},')}mathop{vec{v},'}limits_{(vec{e},')}$ — два разложения вектора vec{v} в одном и том же базисе . Коэффициенты этих разложений совпадают (по теореме 1.5), так как это координаты одного и того же вектора в одном базисе. Поэтому

$mathop{v}limits_{(vec{e})}= mathop{S}limits_{(vec{e})to(vec{e},')}cdot mathop{vec{v},'}limits_{(vec{e},')}quad Leftrightarrowquad begin{pmatrix}v_1\v_2\v_3end{pmatrix}=begin{pmatrix}s_{11}&s_{12}&s_{13}\s_{21}&s_{22}&s_{23}\s_{31}&s_{32}&s_{33}end{pmatrix}!cdot !begin{pmatrix}v'_1\v'_2\v'_3end{pmatrix}.$

(2.4)

Формула (2.4) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.

Аналогично находится связь координат вектора на плоскости при замене базиса:

$mathop{v}limits_{(vec{e})}= mathop{S}limits_{(vec{e})to(vec{e},')}cdot mathop{v'}limits_{(vec{e},')}quad Leftrightarrowquad begin{pmatrix} v_1\v_2end{pmatrix}=begin{pmatrix}s_{11}&s_{12}\s_{21}&s_{22}end{pmatrix}!cdot !begin{pmatrix}v'_1\v'_2end{pmatrix}.$

(2.5)

где $begin{pmatrix} v_1\v_2 end{pmatrix}!,, begin{pmatrix} v'_1\v'_2end{pmatrix}$ — координатные столбцы вектора vec{v} относительно базисов $(vec{e})= begin{pmatrix} vec{e}_1& vec{e}_2 end{pmatrix}$ и $(vec{e},')= begin{pmatrix} vec{e},'_1&vec{e},'_2end{pmatrix}$ на плоскости соответственно, $mathop{S}limits_{(vec{e})to(vec{e},')}= begin{pmatrix}s_{11}&s_{12}\s_{21}&s_{22}end{pmatrix}$ — матрица перехода от базиса к базису .

Матрица перехода от одного базиса к другому обладает следующими свойствами.

1. Пусть в пространстве имеются три базиса (vec{e}),(vec{f}),(vec{g}) и известны матрицы перехода: $mathop{S}limits_{(vec{e})to(vec{f})}$ от базиса к базису ; $mathop{S}limits_{(vec{f})to(vec{g})}$ от к ; $mathop{S}limits_{(vec{e})to(vec{g})}$ от к . Тогда матрица $mathop{S}limits_{(vec{e})to(vec{g})}$ композиции преобразований базисов и равна произведению матриц преобразований базисов:

$mathop{S}limits_{(vec{e})to(vec{g})}= mathop{S}limits_{(vec{e})to(vec{f})}cdot mathop{S}limits_{(vec{f})to(vec{g})}.$

(2.6)

2. Если $mathop{S}limits_{(vec{e})to(vec{f})}$ -матрица перехода от базиса к базису , то матрица $mathop{S}limits_{(vec{e})to(vec{f})}$ обратимая (невырожденная) и обратная матрица является матрицей перехода от базиса к базису $(vec{e})colonmathop{S^{-1}}limits_{(vec{e})to(vec{f})}=mathop{S}limits_{(vec{f})to(vec{e})}$ . Координаты вектора vec{v} в базисах и связаны формулами:

$mathop{v}limits_{(vec{e})}=mathop{S}limits_{(vec{e})to(vec{f})}cdotmathop{v}limits_{(vec{f})},qquad mathop{v}limits_{(vec{f})}= mathop{S^{-1}}limits_{(vec{e})to(vec{f})}cdotmathop{v}limits_{(vec{e})}=mathop{S}limits_{(vec{f})to(vec{e})}cdotmathop{v}limits_{(vec{e})}.$

3. Определитель матрицы $mathop{S}limits_{(vec{f})to(vec{g})}$ перехода от базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2&vec{f}_3end{pmatrix}$ к базмсу $(vec{g})=begin{pmatrix}vec{g}_1&vec{g}_2&vec{g}_3end{pmatrix}$ равен отношению ориентированных объемов параллелепипедов, построенных на базисных векторах (рис.2.8,а):

$detmathop{S}limits_{(vec{f})to(vec{g})}=frac{(vec{g}_1,vec{g}_2,vec{g}_3)}{(vec{f}_1,vec{f}_2,vec{f}_3)}.$

Определитель матрицы $mathop{S}limits_{(vec{f})to(vec{g})}$ перехода от базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ на плоскости к базису $(vec{g})=begin{pmatrix}vec{g}_1&vec{g}_2end{pmatrix}$ равен отношению ориентированных площадей параллелограммов, построенных на базисных векторах (рис.2.8,б):

$detmathop{S}limits_{(vec{f})to(vec{g})}=frac{vec{g}_1landvec{g}_2}{vec{f}_1landvec{f}_2}.$

Определитель матрицы перехода положительный, если эти базисы одноименные (оба правых или оба левых), и отрицательный, если базисы разноименные (один правый, а другой левый).

Ориентированные площади и объёмы параллелограммов, построенные на базисных векторах

4. Любая невырожденная квадратная матрица (2-го или 3-го порядков) может служить матрицей перехода от базиса к базису (на плоскости или в пространстве соответственно).

Докажем первое свойство. Запишем связь (2.4) для данных базисов:

$(vec{f})=(vec{e})cdotmathop{S}limits_{(vec{e})to(vec{f})};qquad (vec{g})=(vec{f})cdotmathop{S}limits_{(vec{f})to(vec{g})};qquad (vec{g})=(vec{e})cdotmathop{S}limits_{(vec{e})to(vec{g})}.$

Подставляя первое выражение во второе равенство, получаем $(vec{g})=(vec{e})cdotmathop{S}limits_{(vec{e})to(vec{f})}cdotmathop{S}limits_{(vec{f})to(vec{g})}$ . Сравнивая с третьим равенством, приходим к (2.6).

Докажем второе свойство. Пусть $mathop{S}limits_{(vec{f})to(vec{e})}$ — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису (vec{e} — единичная, применяем свойство 1 к трем базисам $(vec{e}),(vec{f}),(vec{e})colon E=mathop{S}limits_{(vec{e})to(vec{f})}cdotmathop{S}limits_{(vec{f})to(vec{e})}$ . Для трех базисов (vec{f}),(vec{e}),(vec{f}) аналогично получаем: $E=mathop{S}limits_{(vec{f})to(vec{e})}cdotmathop{S}limits_{(vec{e})to(vec{f})}$ . Следовательно, $mathop{S}limits_{(vec{f})to(vec{e})}=mathop{S^{-1}}limits_{(vec{e})to(vec{f})}$ (см.разд.П.9).

Докажем третье свойство для базисов в пространстве. Пусть $mathop{F}limits_{(vec{e})to(vec{f})}=begin{pmatrix}f_{11}&f_{12}&f_{13}\f_{21}&f_{22}&f_{23}\f_{31}&f_{32}&f_{33}end{pmatrix}$ матрица перехода от стандартного базиса (vec{e})=begin{pmatrix}vec{i}&vec{j}&vec{k}end{pmatrix} к базису $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2&vec{f}_3end{pmatrix}$ , где $vec{f}_1=f_{11}vec{i}+f_{21}vec{j}+f_{31}vec{k}$ , $vec{f}_2=f_{12}vec{i}+f_{22}vec{j}+f_{32}vec{k}$ , $vec{f}_3=f_{13}vec{i}+f_{23}vec{j}+f_{33}vec{k}$ . По формуле (1.20) ориентированный объем параллелепипеда, построенного на векторах $vec{f}_1,vec{f}_2,vec{f}_3$ смешанному произведению $(vec{f}_1,vec{f}_2,vec{f}_3)$ или, что то же самое, определителю $detmathop{F}limits_{(vec{e})to(vec{f})}$ . Аналогично, если $mathop{G}limits_{(vec{e})to(vec{g})}$ — матрица перехода от стандартного базиса к базису $(vec{g})=begin{pmatrix}vec{g}_1&vec{g}_2&vec{g}_3end{pmatrix}$ , то $detmathop{G}limits_{(vec{e})to(vec{g})}=(vec{g}_1,vec{g}_2,vec{g}_3)$ . Из первых двух свойств матрицы перехода следует, что $mathop{S}limits_{(vec{f})to(vec{g})}=mathop{F^{-1}}limits_{(vec{e})to(vec{f})}cdotmathop{G}limits_{(vec{e})to(vec{g})}$ . По свойствам определителя (см. разд.П.9)

$detmathop{S}limits_{(vec{f})to(vec{g})}=detmathop{F^{-1}}limits_{(vec{e})to(vec{f})}cdotdetmathop{G}limits_{(vec{e})to(vec{g})}=frac{detmathop{G}limits_{(vec{e})to(vec{g})}}{detmathop{F}limits_{(vec{e})to(vec{f})}}=frac{(vec{g}_1,vec{g}_2,vec{g}_3)}{(vec{f}_1,vec{f}_2,vec{f}_3)},$ что и требовалось доказать.

Преобразование координат точки при замене системы координат

Связь координат одной и той же точки в разных системах координат в пространстве

Пусть в пространстве заданы две системы координат $Ovec{e}_1,vec{e}_2,vec{e}_3$ (старая) и $Ovec{e},'_1,vec{e},'_2,vec{e},'_3$ (новая), известна матрица (2.2) перехода от базиса (vec{e}) к базису (vec{e},') , а также координаты вектора переноса начала координат vec{s}=overrightarrow{OO'} в старом базисе :

$vec{s}=overrightarrow{OO'}=s_1cdotvec{e}_1+s_2cdotvec{e}_2+s_3cdotvec{e}_3.$

Пусть X(x_1,x_2,x_3) и X(x'_1,x'_2,x'_3) — координаты точки относительно старой и новой систем координат. Требуется найти формулы, связывающие старые и новые координаты точки (рис.2.9).

Запишем векторное равенство overrightarrow{OX}= overrightarrow{OO'}+ overrightarrow{O'X} в координатной форме (в старом базисе (vec{e}) ), учитывая, что координаты радиус-вектора совпадают с координатами точки, а старые и новые координаты вектора overrightarrow{O'X} связаны формулой (2.4). Получим

$begin{pmatrix} x_1\x_2\x_3 end{pmatrix}= begin{pmatrix} s_1\s_2\s_3 end{pmatrix}+ begin{pmatrix} s_{11}& s_{12}& s_{13}\ s_{21}& s_{22}& s_{23}\ s_{31}& s_{32}& s_{33} end{pmatrix}!cdot! begin{pmatrix}x'_1\x'_2\x'_3end{pmatrix}~~ Leftrightarrow~~ mathop{x}limits_{(vec{e})}= mathop{s}limits_{(vec{e})}+ mathop{S}limits_{(vec{e})to (vec{e},')} cdot mathop{x'}limits_{(vec{e},')}.$

(2.7)

Формула (2.7) устанавливает связь координат одной и той же точки в разных системах координат в пространстве, выражая старые координаты через новые.

Аналогичная формула

$begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix} s_1\s_2 end{pmatrix}+ begin{pmatrix} s_{11}& s_{12}\ s_{21}& s_{22} end{pmatrix}!begin{pmatrix}x'_1\x'_2end{pmatrix}~~ Leftrightarrow~~ mathop{x}limits_{(vec{e})}= mathop{s}limits_{(vec{e})}+ mathop{S}limits_{(vec{e})to (vec{e},')}cdot mathop{x'}limits_{(vec{e},')}.$

(2.8)

устанавливает связь координат одной и той же точки в разных системах координат на плоскости, выражая старые координаты через новые.

Формулы вида (2.7) или (2.8): x=s+Scdot x' с любой невырожденной матрицей задают аффинное преобразование координат на плоскости или в пространстве. По этим формулам можно для любой старой системы координат установить новую систему координат, поскольку известен вектор vec{s}=overrightarrow{OO'} переноса начала координат (координатный столбец ) и координаты новых базисных векторов в старом базисе (координатные столбцы являются столбцами матрицы ), и наоборот, по новой системе координат восстановить старую.

Пример 2.4. В прямоугольной системе координат Ovec{i}vec{j} на плоскости заданы векторы $vec{f}_1=2vec{i}+vec{j},$ $vec{f}_2=-vec{i}+2vec{j}$ и точки O'(3,1),~A(-1,3) (рис.2.10).Требуется найти:

Векторы в прямоугольной системе координат на плоскости

а) матрицу перехода $mathop{S}limits_{(vec{e})to(vec{f})}$ от стандартного базиса (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} к базису $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ ;

б) ориентацию базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ ;

в) матрицу перехода $mathop{S}limits_{(vec{e})to(vec{f},')}$ от стандартного базиса (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} к базису $(vec{f},')=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ ;

г) матрицу перехода $mathop{S}limits_{(vec{f})to(vec{e})}$ от базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ к базису (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} ;

д) координаты вектора vec{a}=overrightarrow{OA} в базисе (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} ;

е) координаты точки в системе координат $O'vec{f}_1vec{f}_2$ .

Решение. а) Составляем искомую матрицу $mathop{S}limits_{(vec{e})to(vec{f})}$ , записывая координаты векторов $vec{f}_1,vec{f}_2$ по столбцам: $mathop{S}limits_{(vec{e})to(vec{f})}=begin{pmatrix}2&-1\1&2end{pmatrix}$ .

б) Определитель найденной матрицы $mathop{S}limits_{(vec{e})to(vec{f})}$ положительный: $detmathop{S}limits_{(vec{e})to(vec{f})}=begin{vmatrix}2&-1\1&2end{vmatrix}=5$ , поэтому базис $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ ориентирован также как стандартный (см. свойство 3 матрицы перехода), т.е. является правым.

в) Составляем искомую матрицу $mathop{S}limits_{(vec{e})to(vec{f},')}$ , записывая координаты векторов $vec{f}_1,vec{f}_2$ (в указанном порядке) по столбцам: $mathop{S}limits_{(vec{e})to(vec{f},')}=begin{pmatrix}-1&2\2&1end{pmatrix}$ .

г) Учитывая свойство 2, матрицей перехода от базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ к базису (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} служит матрица, обратная для $mathop{S}limits_{(vec{e})to(vec{f})}$ :

$mathop{S}limits_{(vec{f})to(vec{e})}=mathop{S^{-1}}limits_{(vec{e})to(vec{f})}=frac{1}{5}begin{pmatrix}2&1\-1&2end{pmatrix}=begin{pmatrix}0,!4&0,!2\-0,!2&0,!4end{pmatrix}.$

д) Вектор vec{a}=overrightarrow{OA} является радиус-вектором точки , поэтому известны его координаты (-1,3) в стандартном базисе (vec{e})=begin{pmatrix}vec{i}&vec{j}end{pmatrix} . Составим координатный столбец $a=begin{pmatrix}-1\3end{pmatrix}$ вектора vec{a} в стандартном базисе. Координатный столбец этого вектора относительно базиса $(vec{f})=begin{pmatrix}vec{f}_1&vec{f}_2end{pmatrix}$ связан с его координатным столбцом формулой $a'=mathop{S^{-1}}limits_{(vec{e})to(vec{f})}cdot a$ , следующей из свойства 2 матрицы перехода. Учитывая пункт “г”, вычисляем

$a'=mathop{S^{-1}}limits_{(vec{e})to(vec{f})}cdot a=begin{pmatrix}0,!4&0,!2\-0,!2&0,!4end{pmatrix}!begin{pmatrix}-1&3end{pmatrix}=begin{pmatrix}0,!2\1,!4end{pmatrix}$ , то есть $vec{a}=0,!2cdotvec{f}_1+1,!4cdotvec{f}_2$ .

е) Составляем координатный столбец $s=begin{pmatrix}3\1end{pmatrix}$ , вектора vec{s}=overrightarrow{OO'} (радиус-вектор точки ) и записываем связь (2.8):

$begin{pmatrix}-1\3end{pmatrix}=begin{pmatrix}3\1end{pmatrix}+begin{pmatrix}2&-1\1&2end{pmatrix}!begin{pmatrix}x'_1\x'_2end{pmatrix}Leftrightarrowbegin{cases}2x'_1-x'_2=-4,\x'_1+2x'_2=2.end{cases}$

Решая эту систему, находим координаты x'_1=-1,!2;~x'_2=1,!6 точки в системе координат $O'vec{f}_1vec{f}_2$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Мы vkontakte.ru

Друзья

Словарь синонимов русского языка

Аффинное преобразование и его матричное представление

Тема этого выпуска задание аффинного преобразования в матричной форме. Эта
тема, по сути, является обобщением всего, что было сказано ранее.

Определение. Преобразование плоскости называется аффинным,
если

оно взаимно однозначно;
образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

разные точки переходят в разные;
в каждую точку переходит какая-то
точка.

Прим. Более подробно про аффинные преобразования
можно посмотреть на ru.wikibooks.org

Однородные координаты

Если рассмотреть параллельный перенос, то оказывается, что для его задания
матрицы 2×2 уже недостаточно. Но его можно задать с помощью матрицы размера
3×3. Появляется вопрос, откуда взять третью координату у двумерной точки?

Определение. Однородные координаты — координаты, обладающие тем свойством,
что определяемый ими объект не меняется при умножении всех координат на одно и
то же число.

Однородными координатами вектора (х, у) является тройка чисел (x’, y’, h), где х = х’ / h, у = y’/h, а h — некоторое вещественное число (случай,
когда h = 0 является особым).

Прим. Данные координаты не позволяют однозначно
задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки
плоскости.

Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим
некоторые преобразования в однородных координатах.

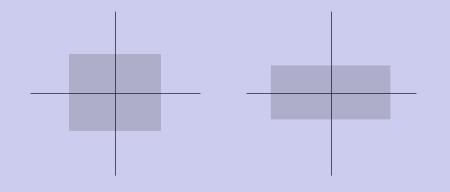
Сжатие/растяжение

Это преобразование умножает
соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (a_x * x, a_y * y). Матрица преобразования запишется следующим образом:

[ a_x 0 0 ]

[ 0 a_y 0 ]

[ 0 0 1 ]

Где a_x– растяжение по оси x,

a_y – растяжение по оси y.

Прим. Можно заметить, что при отрицательных
значениях коэффициентов сжатия/растяжения происходит отражение относительно
соответствующих осей. Этот случай можно включить в данное преобразование, а
можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают
только положительные значения.

Поворот

Матрица поворота 2×2 была подробно
разобрана ранее. Теперь она дополняется строкой и столбцом:

[ cos(phi) sin(phi)
0 ]

[ -sin(phi) cos(phi) 0 ]

[ 0 0 1 ]

Прим.
При угле phi = п эта матрица задает центральную симметрию относительно начала координат,
которая является частным случаем поворота. Можно заметить, что такую симметрию
можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные
коэффициенты масштабирования).

Параллельный перенос

Исходный вектор (x, y) переходит в (x + tx, y + ty).
Матрица преобразования запишется следующим образом:

[ 1 0 0 ]

[ 0 1 0 ]

[ t_x t_y 1 ]

Отражение

Как говорилось в примечании к
преобразованию сжатия/растяжения, отражения получаются следующим образом:

[ -1 0 0 ]

[ 0 1 0 ]

[ 0 0 1 ]
отражение относительно оси x

[ 1 0 0 ]

[ 0 -1 0 ]

[ 0 0 1 ]
отражение относительно оси y

Общий вид аффинного преобразования

Матрица 3×3, последний столбец которой равен ( 0 0 1 )^T, задает аффинное преобразование плоскости:

[ * * 0 ]

[ * * 1 ]

По одному из свойств, аффинное
преобразование можно записать в виде:

f(x) = x * R + t,

где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных
координатах это запишется следующим образом:

[ R_1,1 R_1,2 0 ]

[ R_2,1 R_2,2 0 ]

[ t_x t_y 1 ]

Если умножить вектор-строку на эту матрицу
получаем результат преобразования:

[ x
y 1 ] * [ R_1,1 R_1,2 0 ]

[ R_2,1 R_2,2 0 ]

[ t_x t_y 1 ]

[ x’
y’ 1 ] + [ t_x t_y1]

При этом [ x’ y’ ]
= R * [ x y ]

Прим. Любопытный читатель уже задал себе
вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади
всех фигур изменяются в |R|.
(Можно строго доказать это с точки зрения математики, но здесь этот факт
приводится без доказательства.)

Т.о. аффинное преобразование
представляется в виде композиции некоторого преобразования, задаваемого
матрицей R, и параллельного
переноса. Разберем более подробно природу этой матрицы и возможности, которые
она нам дает.

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R_1,1,R_1,2), вектор (0, 1) переходит в (R_2,1,R_2,2). Новый базис это строки матрицы R.

Пример.

При отражении относительно оси

y, базисный вектор по оси ординат
сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом:

[ -1 0 ]

[ 0 1 ]

Теперь становится ясно, что кроме
вышеперечисленных преобразований, с помощью аффинного преобразования можно
получить скос:

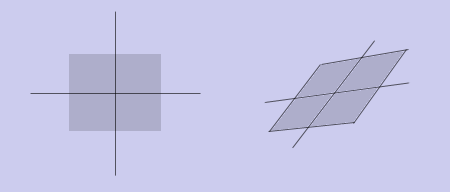
Выше приведены базовые сведения о таком
мощном инструменте, как аффинное преобразование. Остается много вопросов: какой
подкласс аффинных преобразований сохраняет углы между прямыми? Как можно
представить аффинное преобразование в виде композиции нескольких подклассов? Как
задавать более сложные преобразования, например, осевая симметрия относительно
произвольной прямой?

Ответы на эти вопросы и более детальное
рассмотрение аффинного преобразования будут приведены отдельно, в качестве
раздела курса теоретической геометрии.

Остановимся на практической реализации
аффинного преобразования в виде демонстрационной программы. К возможностям
приложения, демонстрирующего поворот плоскости мышью, добавляются функции
параллельного переноса при нажатой клавише CTRL.

Т.к. эта статья является завершающей в
данном разделе, код демонстрационного приложения должен быть соответствующим. Давайте
попробуем разобраться, какие блоки нужны в графическом приложении, параллельно
рассматривая, как они реализованы в данной программе:

блок, в котором происходит создание
окна и обрабатываются сообщения операционной системы, реализован в файлe main.cpp
графический движок, выполняющий
отрисовку изображения, класс Engine
прослойка, необходимая для
преобразования логических координат в оконные и обратно, класс Viewport
объект, отвечающий за реакцию на действия
пользователя, класс Action

В приведенном примере реализованы
эти функциональные блоки, с подробными комментариями.

Скачать исходный текст демонстрационной программы

Источник

Мы будем далее предполагать,
что в пространстве задана декартова
система координат .
В такой системе координат точки задаются
тройками чисел,
которые нам будет удобно записывать в
виде столбцов вида.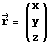

Нас будут интересовать так
называемыеиаффинные
преобразования
пространства. Это такие преобразования,
при которых все прямые преобразуются
снова в прямые. Оказывается, что все
такие преобразования можно записать
формулами вида

где –
координаты исходной точки; те же буквы
со звёздочкой наверху обозначают
координаты точки, которая получается
в результате преобразования. Для
компактной записи этих формул весьма
полезно использовать матричные
обозначения. Именно, определим матрицу
и три столбца следующим образом:

Тогда приведённое выше
преобразование можно записать в форме
простого матричного равенства .
В дальнейшем мы все преобразования
будем записывать в такой форме, указывая
при необходимости вид матрицы.

Самым
простым преобразованием такого вида
является параллельный
сдвиг на
вектор ,
который определяется
формулой.
Матрицав
этом случае совпадает с единичной
матрицей.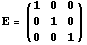

Сдвиг
на ненулевой вектор не имеет неподвижных
точек.
В общем случае можно определить,
имеет ли преобразование неподвижные
точки, решая систему уравнений ,
где–
единичная матрица. Заметим, что если
матрицаневырожденная,
то есть, её определитель не равен,
то эта система имеет единственное
решение,
так что преобразование имеет единственную
неподвижную точку.

Если векторнулевой,
то преобразование имеет вид.
Такое преобразование оставляет
неподвижным начало координат.

Если
мы уже нашли преобразование нужного
вида (с матрицей ),
оставляющее неподвижным начало координат,
то очень легко найти преобразование
такого же вида, оставляющее неподвижной
заданную точку.
Такое преобразование будет иметь вид.
Поэтому в дальнейшем мы будем ограничиваться
преобразованиями, оставляющими
неподвижным именно начало кординат, то
есть, преобразованиями вида.

Другой
простейший тип преобразований
– растяжения (сжатия)
вдоль прямой.
Растяжение вдоль оси враз
задаётся, соответственно, матрицей

(при получается
сжатие). Растяжение одновременно по
всем осям (вообще говоря, в разное число
раз) задаётся матрицей

Если все диагональные
элементы в этой матрице одинаковые, то
получается равномерное растяжение
(сжатие), то есть, преобразование подобия.

Симметрии относительно
плоскостей ,
осейи
точки(начала
координат) задаются матрицами

Симметрии относительно
произвольных плоскостей и прямых можно
получить по той же формуле, что и
растяжения, взяв в качестве нужную
комбинацию чисели.
Однако если мы хотим, чтобы полученное
преобразование было действительно
симметрией нужного вида, векторы,
для которых,
должны быть перпендикулярны, то есть,
их скалярное произведение должно быть
равно:.

При отыскании нужных векторов
полезно иметь в виду, что вектор с
координатами перпендикулярен
плоскости.
В
частности, матрица симметрии относительно
плоскостиимеет
вид

Более
сложным классом преобразований
являются движения,
то есть, преобразования, сохраняющие
расстояния между точками. Матрица,
определяющая движение, является ортогональной,
то есть, удовлетворяет условию.
Это означает, что обратная матрица
должна совпадать с транспонированной.
Все
движения можно разбить на две
группы: собственные движения,
которые являются комбинациями вращений
и сдвигов и характеризуются тем, что
определитель матрицыравен,
и несобственные движения, которые
включают дополнительно симметрию
относительно плоскости или точки и
характеризуются тем, что определитель
матрицыравен.

Заметим,
что симметрию относительно прямой можно
рассматривать как вращение вокруг этой
прямой на угол ,
так что такие симметрии являются
собственными движениями.

Собственные
движения, имеющие неподвижную точку,
называются вращениями.
Как мы и договорились, будем предполагать,
что эта неподвижная точка совпадает с
началом координат .

Самый простой случай –
поворот вокруг оси координат на заданный
угол. Матрица поворота на угол вокруг
осисоответственно
имеет следующий вид:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Что за зверь — аффинные преобразования?

Что такое аффинное преобразование?

Примеры аффинных преобразований

Поворот

Растяжение-сжатие

Сдвиг

Эпилог

Ссылки по теме

Поворот

Сдвиг

Перемещение и масштабирование

Композиция

Применение

Центр трансформации

Аффинное преобразование Windows

Композиция

Практика

Аффинный поворот

Аффинный сдвиг

Аффинная композиция

Если б мышь знала… Координаты вершин

Смещать ли начало координат?

Видео + скачать

Аффинные преобразования координат

Преобразование координат вектора при замене базиса

Преобразование координат точки при замене системы координат

Друзья

Аффинное преобразование и его матричное представление

Вам также может понравиться

Как понять найти разность чисел

Как найти деньги в долг у людей

Как найти карася зимой видео

Добавить комментарий Отменить ответ