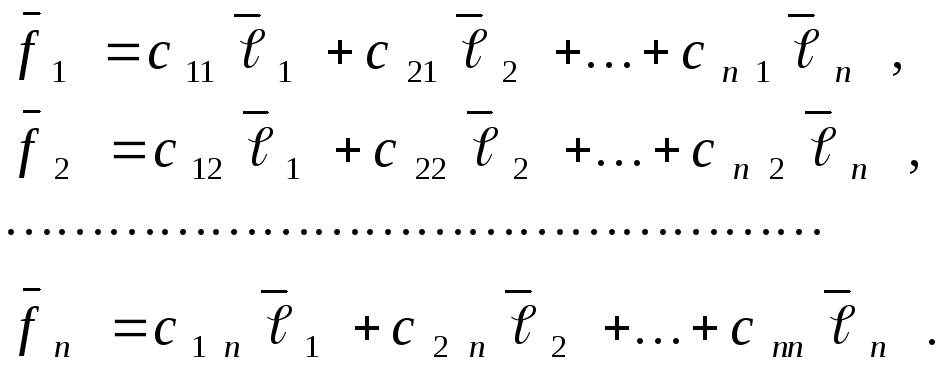Как найти матрицу билинейной формы в базисе - Сайт, где вы сможете решить свои вопросы

Выберем в n-мерном
пространстве
какой-либо базиси выразим билинейную форму

через коэффициенты
ивекторов
и
в этом базисе. Имеем:

В силу свойств а)
и б) пункта
билинейной формы, имеем:

Или, короче:

Обозначим постоянные
через.
Тогда в заданном базисевсякая билинейная форма вn-мерном
пространстве может быть записана в
виде:

.
(5)

ОПРЕДЕЛЕНИЕ 4.
Матрицу
,
составленную из коэффициентовмногочлена (5), называютматрицей
билинейной формы
в
базисе

Таким образом, в
каждом базисе пространства
билинейная форма

определяется своей матрицей:

4.4. Преобразование матрицы билинейной формы при изменении базиса

Пусть даны в
n-мерном
линейном пространстве
два базиса:и.
Причем, векторы второго базисавыражаются через векторы базисаформулами:

Матрицу

назовем матрицей
перехода от базиса
к базису.

Пусть
есть матрица билинейной формы

в базисе
,
аматрица той же билинейной формы в базисе.
Наша задача состоит в том, чтобы по
матриценайти матрицу.

По определению
,
то есть– значение билинейной формы

при
.

Для того, чтобы
найти это значение, то есть
, воспользуемся формулой (5), подставив
в нее вместоикоординаты векторовив
базисе,
то есть числаи.
Получим:

.
(6)

Это и есть искомая
формула.

Запишем ее в
матричной форме. Для этого положим
.
Таким образом,является элементами матрицы,
транспонированной к матрицеС.
С учетом этого выражение (6) можно записать
так:

или

Итак, если А
и В
суть матрицы билинейной формы

соответственно в базисах
и.,
то преобразование матрицы билинейной
формы при переходе от одного базиса к
другому будет иметь вид:

где С– матрица
перехода от базисак базису.,
а– транспонированная матрица.

4.5. Квадратичные формы

Пусть –симметричная
билинейная форма.

ОПРЕДЕЛЕНИЕ 1.
Функция
,
которая получается из билинейной формы

,
если положить в ней
=,
называется квадратичной
формой.

Всякая квадратичная
форма
,
в базисе
евклидового пространстваЕ_n
выражается следующей формулой:

,
(7)

где
симметричная матрицаквадратичной
формы и.

В некотором базисе
выражение (7) квадратичной формы может
не содержать произведений
,
то есть

,
(8)

Выражение (8)
называется каноническим видом квадратичной
формы. В частности, если
,
то получаемнормальный
вид
квадратичной
формы
.

Для всякой
квадратичной формы существует такой
базис, в котором она имеет канонический
вид.

4.6. Методы приведения квадратичной формы к каноническому виду

а) Метод Лагранжа
выделения полных квадратов.

Пусть квадратичная
форма
имеет в базисе
вид (7). Для приведения формы

к сумме квадратов методом Лагранжа
рассмотрим случай квадратичной формы,
у которой все коэффициенты

(при квадратах
),

равны нулю и в то же время эта квадратичная
форма не равна тождественно нулю, то
есть в ней есть отличное от нуля хотя
бы одной произведение, например,
.

Выполним
преобразование базиса, при котором
коэффициенты векторов в старом и новом
базисах связаны формулами:

Тогда:

Таким образом,
всегда найдется такой базис, в котором
в записи (7) хотя бы один коэффициент
при квадрате
.отличен
от нуля.

В дальнейшем будем
считать, что
.
(Если,
то отличен от нуля коэффициент при
квадрате какой-нибудь другой координаты
и к рассматриваемому случаю можно
прийти, иначе, занумеровав векторы,
что также является некоторым преобразованием
базиса).

Рассмотрим часть
квадратичной формы, содержащей
,
то есть

Дополним эту сумму
до полного квадрата:

где
есть алгебраическая сумма членов, не
зависящих от.
Если теперь сделать замену

то квадратичная
форма в новом базисе примет вид

В полученной форме
выделено слагаемое
,
а оставшаяся частьА,
является квадратичной формой в
.

Далее эти рассуждения
повторяются для исходной квадратичной
формы

и т.д. Конечным результатом является
то, что она приводится к нормальной
форме.

ПРИМЕР 1.
Методом Лагранжа привести к каноническому
виду квадратичную форму

Первое преобразование:

Тогда получим:

Второе преобразование:

Получим новое
выражение для квадратичной формы:

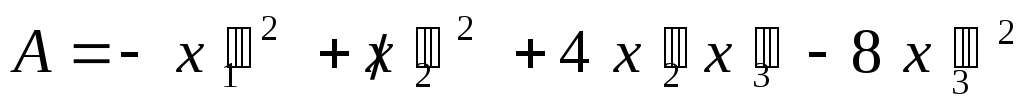
Третье преобразование:

форма примет
канонический вид:

При этом

б) Метод собственных
векторов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 мая 2019 года; проверки требует 1 правка.

Пусть есть векторное пространство над полем (чаще всего рассматриваются поля или ).

Билинейной формой называется функция , линейная по каждому из аргументов:

{displaystyle F(x+z,,y)=F(x,,y)+F(z,,y)}

{displaystyle F(x,,y+z)=F(x,,y)+F(x,,z)}

{displaystyle F(lambda x,,y)=lambda F(x,,y)}

{displaystyle F(x,,lambda y)=lambda F(x,,y)}

здесь и

Билинейная форма — частный случай понятия тензора (тензор ранга (0,2)).

Альтернативное определение[править | править код]

В случае конечномерных пространств (например, $mathbb {R} ^{n}$ ) чаще используется другое определение.

Пусть есть множество векторов вида $x=(x_{1},x_{2},dots ,x_{n}),$ где $x_{i}in K,i=overline {1,n}$ .

Билинейными формами называются функции вида

$F(x,y)=sum _{{i,,j=1}}^{n}a_{{ij}}x_{i}y_{j},$

где $x=(x_{1},x_{2},dots ,x_{n}),$ $y=(y_{1},y_{2},dots ,y_{n}),$ а $a_{{ij}}$ — некоторые константы из поля

Говоря другими словами, билинейная форма — это функция от двух векторов по переменных компонент в каждом, являющаяся однородным многочленом первой степени относительно переменных компонент каждого вектора.

Связанные определения[править | править код]

Свойства[править | править код]

${begin{pmatrix}F(e_{1},,e_{1})&F(e_{1},,e_{2})&ldots &F(e_{1},,e_{n})\F(e_{2},,e_{1})&F(e_{2},,e_{2})&ldots &F(e_{2},,e_{n})\vdots &vdots &ddots &vdots \F(e_{n},,e_{1})&F(e_{n},,e_{2})&ldots &F(e_{n},,e_{n})end{pmatrix}},$

так что для любых векторов $x=x^{1}e_{1}+x^{2}e_{2}+cdots +x^{n}e_{n}$ и $y=y^{1}e_{1}+y^{2}e_{2}+cdots +y^{n}e_{n}$

$F(x,,y)={begin{pmatrix}x^{1}&x^{2}&ldots &x^{n}end{pmatrix}}{begin{pmatrix}F(e_{1},,e_{1})&F(e_{1},,e_{2})&ldots &F(e_{1},,e_{n})\F(e_{2},,e_{1})&F(e_{2},,e_{2})&ldots &F(e_{2},,e_{n})\vdots &vdots &ddots &vdots \F(e_{n},,e_{1})&F(e_{n},,e_{2})&ldots &F(e_{n},,e_{n})end{pmatrix}}{begin{pmatrix}y^{1}\y^{2}\vdots \y^{n}end{pmatrix}},$

то есть

$F(x,,y)=sum _{{i,j=1}}^{n}f_{{ij}},x^{i}y^{j}, quad f_{{ij}}=F(e_{i},,e_{j}).$

Преобразование матрицы билинейной формы при замене базиса[править | править код]

Матрица, представляющая билинейную форму в новом базисе, связана с матрицей, представляющей её в старом базисе, через матрицу, обратную матрице перехода к новому базису (матрице Якоби), через которую преобразуются координаты векторов.

Иными словами, если координаты вектора в старом базисе ${displaystyle X^{i}}$ выражаются через координаты в новом x^i через матрицу beta
${displaystyle X^{i}=sum beta _{j}^{i}x^{j}}$ , или в матричной записи , то билинейная форма на любых векторах и запишется, как

$F(x,,y)=sum _{{i,j}}F_{{ij}}X^{i}Y^{j}=sum _{{i,j,k,m}}F_{{ij}}beta _{k}^{i}beta _{m}^{j}x^{k}y^{m}$

то есть компоненты матрицы, представляющей билинейную форму в новом базисе, будут:

$f_{{km}}=sum _{{i,j}}F_{{ij}}beta _{k}^{i}beta _{m}^{j}$

или, в матричной записи:

${displaystyle f=beta ^{T}Fbeta }$

${displaystyle beta =alpha ^{-1}}$

, где

— матрица прямого преобразования координат

Связь с тензорными произведениями и функтором Hom[править | править код]

Из универсального свойства тензорного произведения следует, что билинейные формы на V находятся во взаимно-однозначном соответствии со множеством , где k — основное поле.

Так как функтор тензорного произведения и функтор Hom являются сопряженными, , то есть билинейной форме соответствует линейное отображение из в двойственное пространство V^* . Это соответствие может быть проведено двумя путями (так как существует два функтора тензорного произведения — с зафиксированным левым аргументом и с зафиксированным правым), их часто обозначают как

${displaystyle B_{1}({mathsf {v}})=B({mathsf {v}},cdot )}$

${displaystyle B_{2}({mathsf {v}})=B(cdot ,{mathsf {v}})}$ .

См. также[править | править код]

Квадратичная форма
Билинейная операция
Билинейное преобразование

Литература[править | править код]

Мальцев А. И. Основы линейной алгебры. — М.: Наука, 1975.
Гельфанд И. М. Лекции по линейной алгебре. — М.: Наука, 1971.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Беклемишев Д. В. Аналитическая геометрия и линейная алгебра. — М.: Высш. шк., 1998. — 320 с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Источник

§ 1. Билинейные формы

Определение билинейной формы и ее различные формы записи

Определение. Билинейной формой на линейном пространстве над полем называется функция двух векторных аргументов, принимающая значения из поля , линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям:

1*. ;

2*. ;

3*. ;

4*. .

Рассмотрим N-мерное линейное пространство и выберем в нем какой-либо базис

(1)

Каждый вектор пространства можно разложить по этому базису: . Тогда

. (2)

Из (2) видно, Что значение билинейной формы для любых двух векторов и выражается через координаты этих векторов и некоторые числа , которые с аргументами и никаким образом не связаны, а зависят только от выбранного базиса. Обозначим

. (3)

Из (2) вытекает:

. (4)

Равенство (4) называется координатной формой записи билинейной формы.

Определение. Матрицей билинейной формы в базисе (1) называется матрица , где .

Обозначим, как обычно,

, —

Координатные столбцы векторов и соответственно в заданном базисе. Заметим, что — это число, которое можно рассматривать как матрицу размеров . В таком случае, (4) можно переписать и так: , откуда вытекает, что

. (5)

Равенство (5) называется матричной формой записи билинейной формы.

Итак, если в задан базис, то каждой билинейной форме на линейном пространстве соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.

Теорема 1. Пусть в линейном пространстве задан какой-либо базис (1). Тогда для любой квадратной матрицы , на линейном пространстве существует единственная билинейная форма , матрица которой в заданном базисе совпадает с В, то есть такая, для которой выполняется условие (3).

►Построение. Положим по определению:

Линейность.

;

Таким образом, линейность по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.

Выполнение условия (3). Так как (то есть I-я координата вектора равна , а J –я координата вектора — ). Поэтому .

Единственность. Предположим, что существует еще одна билинейная форма , не совпадающая с формой , для которой выполняется (3). Тогда

И мы пришли к противоречию.◄

Таким образом, если в задан какой-либо базис, то между множеством билинейных форм на линейном пространстве и множеством квадратных матриц N-го порядка с элементами из поля Р устанавливается взаимно однозначное соответствие.

Изменение матрицы билинейной формы при изменении базиса

Теорема 2. Пусть в линейном пространстве заданы два базиса:

(6)

, (7)

И пусть и — матрицы билинейной формы в базисах (6) и (7) соответственно. Тогда

, (8)

Где Т – матрица перехода от (6) к (7).

►Воспользуемся определением билинейной формы и ее матрицы:

. (9)

Заметим, что в правой части равенства (9) индекс должен соответствовать номеру строки, а индекс — номеру столбца (по согласованию с левой частью), поэтому из (9) и вытекает равенство (8).◄

Следствие. Если матрица билинейной формы в одном из базисов пространства невырождена, то в любом другом базисе матрица этой билинейной формы также невырождена.

Определение. Билинейная форма на линейном пространстве называется Невырожденной, если ее матрица в некотором, а значит, и в любом базисе пространства невырождена.

Определение. Квадратные матрицы и называются Конгруэнтными, если они связаны соотношением (8), где — невырожденная матрица.

Таким образом, матрицы одной и той же билинейной формы в различных базисах конгруэнтны.

Симметричные билинейные формы

Определение. Квадратная матрица называется Симметричной, если , или, если .

Лемма. Если матрица симметрична, то любая конгруэнтная ей матрица тоже симметрична.

►Пусть — симметричная матрица, — конгруэнтная ей. Тогда

.◄

Определение. Билинейная форма на линейном пространстве V называется Симметричной, если .

Теорема 3. Для того чтобы билинейная форма на линейном пространстве была симметричной, необходимо и достаточно, чтобы ее матрица в некотором, а значит, и в любом базисе пространства была симметричной.

►Докажем утверждение для некоторого базиса, а для произвольного оно будет вытекать из доказанной леммы. Обозначим матрицу билинейной формы в базисе.

Необходимость. Дано: — симметричная билинейная форма. Тогда и, таким образом, В — симметричная матрица.

Достаточность. Дано: В – симметричная матрица, то есть, . Тогда =.◄

Замечание. При доказательстве теоремы 3 мы также доказали, что преобразование конгруэнтности сохраняет свойство матрицы быть симметричной.

§ 2. Квадратичные формы

Определение. Квадратичной формой, соответствующей симметричной билинейной форме на линейном пространстве V, называется функция одного векторного аргумента .

Пусть задана квадратичная форма , — соответствующая ей симметричная билинейная форма. Тогда

Откуда вытекает, что по квадратичной форме соответствующая ей симметричная билинейная форма тоже определяется однозначно. Итак, между симметричными билинейными и квадратичными формами на линейном пространстве V устанавливается взаимно однозначное соответствие, поэтому квадратичные формы можно изучать с помощью симметричных билинейных.

Рассмотрим N-мерное линейное пространство . Матрицей квадратичной формы в заданном базисе линейного пространства называется матрица соответствующей ей симметричной билинейной формы в том же базисе. Матрица квадратичной формы всегда симметрична.

Обозначим матрицу квадратичной формы в некотором базисе пространства . Если, как обычно, обозначить Х координатный столбец вектора в том же базисе, то в матричном виде квадратичная форма запишется так:

. (1)

Теорема 1. Пусть в линейном пространстве заданы два базиса

(2)

, (3)

И пусть и – матрицы квадратичной формы В базисах (2) и (3) соответственно. Тогда , где Т — матрица перехода от (2) к (3).

Доказательство вытекает из теоремы 1 § 1 и определения матрицы квадратичной формы.

В связи с тем, что матрица перехода Т является невырожденной, то при переходе к новому базису ранг матрицы квадратичной формы не меняется. Поэтому можно сформулировать следующее

Определение. Рангом квадратичной формы, заданной на линейном пространстве , называется ранг ее матрицы в некотором, а значит, и в любом базисе пространства (обозначается ).

Теперь запишем квадратичную форму в координатном виде. Для этого вектор разложим по базису (2): . Если — матрица квадратичной формы в том же базисе, то, в соответствие с равенством (4) § 1 имеем:

— (4)

Координатная форма записи квадратичной формы. Распишем (4) подробно при N=3, учитывая, что

. (4′)

Итак, если в задан базис, то квадратичная форма в координатной записи выглядит как однородный многочлен второй степени от N переменных — координат вектора в данном базисе. Этот многочлен называется Видом квадратичной формы в заданном базисе. Но в приложениях часто такие многочлены возникают самостоятельно, без видимой связи с линейными пространствами (например, вторые дифференциалы функций), поэтому мы сформулируем еще одно определение квадратичной формы.

Определение. Квадратичной формой от N переменных называется однородный многочлен второй степени от этих переменных, т. е. функция вида (4). Матрицей квадратичной формы (4) называется симметричная матрица .

Пример составления матрицы квадратичной формы. Пусть

. (5)

Из (4) и (4′) видно, что коэффициент при совпадает с , т. е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что — половина коэффициента при произведении . Таким образом, матрица квадратичной формы (5) выглядит так:

Выберем теперь в пространстве опять два базиса (2) и (3) и обозначим, как обычно, — координатные столбцы вектора в базисах (2) и (3) соответственно. При переходе от базиса (2) к базису (3) координаты вектора меняются по закону:

, (6)

Где — матрица перехода от (2) к (3). Заметим, что матрица — невырожденная. Запишем равенство (6) в координатной форме:

, (7)

Или подробно:

. (8)

С помощью равенств (8) (или (7), что одно и то же) от переменных переходим к переменным .

Определение. Линейным невырожденным преобразованием переменных называется преобразование переменных, заданное системой равенств (7) или (8), или одним матричным равенством (6), при условии, что — невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.

Если в (4) вместо переменных подставить их выражения через переменные По формулам (8), раскрыть скобки и привести подобные, то получим другой однородный многочлен второй степени

В этом случае говорят, что линейное невырожденное преобразование переменных (8) переводит квадратичную форму в квадратичную форму . Значения переменных и , связанные соотношением (6) (или соотношениями (7) либо (8)) будем называть Соответствующими при заданном линейном невырожденном преобразовании переменных.

Определение. Набор переменных называется Нетривиальным, если в нем значение хотя бы одной из переменных отлично от нуля. В противном случае набор переменных называется Тривиальным.

Лемма. При линейном невырожденном преобразовании переменных тривиальному набору переменных соответствует тривиальный набор.

►Из равенства (6), очевидно, вытекает: если , то и . С другой стороны, используя невырожденность матрицы Т, опять же из (6) получаем , откуда видно, что при также и .◄

Следствие. При линейном невырожденном преобразовании переменных нетривиальному набору переменных соответствует нетривиальный набор.

Теорема 1′. Если линейное невырожденное преобразование (6) переводит квадратичную форму с матрицей А в квадратичную форму с матрицей А’, то (другая формулировка теоремы 1).

Следствие. При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака.

Замечание. В отличие от матрицы перехода и матрицы линейного оператора матрица линейного невырожденного преобразования переменных пишется не по столбцам, а по строкам.

Пусть заданы два линейных невырожденных преобразования переменных:

(9)

. (10)

Применим их последовательно:

. (11)

Композицией линейных невырожденных преобразований переменных (9) и (10) называется их последовательное применение, т. е. преобразование переменных Из (11) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.

Определение. Квадратичные формы называются Эквивалентными, если существует линейное невырожденное преобразование переменных, переводящее одну из них в другую.

§ 3 Канонический вид квадратичной формы

Мы уже говорили о том, что в каждом базисе линейного пространства квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.

Каноническим видом квадратичной формы называется такой ее вид, в котором коэффициенты при произведениях разноименных переменных равны 0, то есть при .

Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или -1. Все отличные от нуля коэффициенты при квадратах Нормального вида комплексной квадратичной формы равны 1.

Теорема 1. Для любой квадратичной формы, заданной на линейном пространстве в существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.

Или (другая формулировка этой же теоремы):

Для любой квадратичной формы от N переменных существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, и существует линейное невырожденное преобразование переменных, приводящее ее к нормальному виду.

Теорему 1 мы докажем позже, а сейчас только приведем пример приведения квадратичной формы к каноническому виду методом, который называется Методом Лагранжа или выделения полных квадратов. Он заключается в следующем: выбираем переменную, коэффициент при квадрате которой отличен от 0, и выделяем полный квадрат, включающий в себя все слагаемые с этой переменной. С этой целью записываем перед скобкой число, обратное выбранному коэффициенту, а в скобках — половину производной по выбранной переменной. За скобками остается квадратичная форма, количество переменных которой уже на единицу меньше. После конечного числа шагов получаем канонический вид.

Пример. ▼

Где . Матрица этого линейного преобразования запишется так:

Как видим, она невырождена, значит, и преобразование переменных является невырожденным. Вводя обозначения

Получаем нормальный вид квадратичной формы: .▲

Замечания. 1. На самом деле при применении метода Лагранжа получаем не прямое преобразование, приводящее квадратичную форму к каноническому виду, а обратное, т. е. преобразование, которое выражает не старые переменные через новые, а наоборот.

2.Если все коэффициенты при квадратах исходной квадратичной формы равны нулю, а отличен от нуля, например, коэффициент при произведении , применим вначале следующее преобразование: Матрица этого преобразования выглядит так:

Очевидно, она невырождена, и, поэтому, соответствующее преобразование переменных также будет невырожденным.

Заметим, что канонический вид квадратичной формы определяется неоднозначно, тем не менее, имеет место

Теорема 2 (Закон инерции). Все канонические виды одной квадратичной формы на действительном линейном пространстве имеют одинаковое число положительных коэффициентов и одинаковое число отрицательных коэффициентов. Нормальный вид квадратичной формы определяется однозначно с точностью до порядка следования коэффициентов.

►Доказательство достаточно провести для нормального вида.

Пусть в базисе линейного пространства квадратичная форма имеет вид

, (2)

А в базисе — вид

. (3)

Так как , то достаточно показать, что . Предположим, что это не так. Пусть, например, . Обозначим

, .

Так как а , то сумма не прямая, поэтому , следовательно, . Тогда, так как , то из (2) видно, что Но, так как , то из (3) видно, видно, что Итак, мы пришли к противоречию. Таким образом, . Аналогично доказывается, что , значит, .◄

Замечание. Для квадратичных форм на комплексном линейном пространстве нормальный вид, очевидно, определяется однозначно, т. к. количество отличных от нуля коэффициентов совпадает с рангом квадратичной формы.

§ 4. Знакоопределенные квадратичные формы

В этом параграфе и до конца главы мы будем рассматривать квадратичные формы только на действительных линейных пространствах.

Определения. Квадратичная форма называется Положительно определенной, если она принимает положительные значения для любого нетривиального набора переменных.

Квадратичная форма называется Отрицательно определенной, если она принимает отрицательные значения для любого нетривиального набора переменных.

Квадратичная форма называется Положительно (отрицательно) полуопределенной, если для любого нетривиального набора переменных она принимает либо положительное (отрицательное) значение, либо 0.

Квадратичная форма Знаконеопределена, если существует нетривиальный набор переменных, при которых она принимает положительное значение, и существует нетривиальный набор переменных, при котором она принимает отрицательное значение.

Лемма 1. Эквивалентные квадратичные формы принимают одинаковые значения при соответствующих наборах переменных.

►Пусть квадратичные формы

(1)

(2)

Эквивалентны. Это значит, что существует линейное невырожденное преобразование переменных , переводящее квадратичную форму в квадратичную форму . Тогда, по теореме 1′ § 2, , а значит,

.◄

Следствие. Если квадратичная форма положительно определена, то все эквивалентные ей квадратичные формы также положительно определены.

Лемма 2 (Необходимое условие знакоопределенности). Если квадратичная форма положительно (отрицательно) определена, то все ее коэффициенты при квадратах положительны (отрицательны).

►Пусть квадратичная форма

Положительно определена. Тогда (единица на M-ом месте), следовательно, все коэффициенты при квадратах положительны.◄

Теорема (Первый критерий знакоопределенности). Для того чтобы квадратичная форма была положительно (отрицательно) определенной необходимо и достаточно, чтобы все коэффициенты какого-либо ее канонического вида были положительными (отрицательными).

►Пусть задана квадратичная форма и пусть

=— (3)

Какой-либо ее канонический вид.

Необходимость. Дано: исходная квадратичная форма положительно определена. Тогда, по следствию к лемме 1, форма (3) тоже положительно определена, а значит, по лемме 2, .

Достаточность. Дано: . Тогда, очевидно, для любого нетривиального набора переменных форма (3) принимает только положи

Тельные значения, следовательно, форма (3) положительно определена, и поэтому, положительно определена и исходная квадратичная форма. ◄

Следствие. Матрица положительно определённой квадратичной формы имеет положительный определитель.

►Пусть А – матрица положительно определенной квадратичной формы, А’ – матрица ее канонического вида (3). При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака. Так как ,то и .◄

§ 5. Критерий Сильвестра знакоопределенности

Квадратичных форм

Назовем R— м усечением квадратичной формы

(1)

Квадратичную форму . Пусть

—

Матрица квадратичной формы (1). Главными минорами матрицы А называются ее миноры, расположенные в левом верхнем углу. Будем обозначать главный минор R-го порядка матрицы А. Очевидно, что совпадает с определителем матрицы квадратичной формы .

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной необходимо и достаточно, чтобы все главные миноры ее матрицы были положительными. Для того чтобы квадратичная форма была отрицательно определенной необходимо и достаточно, чтобы все главные миноры ее матрицы нечетного порядка были отрицательными, а четного – положительными.

►Доказательство для положительной определенности.

Необходимость. Дано: квадратичная форма K положительно определена. Тогда для любого нетривиального набора переменных , значит, положительно определена и квадратичная форма , и поэтому на основании следствия к теореме §4.

Достаточность. Дано: . Доказательство проведем методом математической индукции по количеству переменных.

A) Проверяем утверждение при . Имеем: , т. е. квадратичная форма K положительно определена.

В) Пусть утверждение верно для квадратичных форм от (N-1)-й переменной. Докажем его для квадратичных форм от N переменных.

Так как , то, по предположению индукции, квадратичная форма положительно определена, а значит, существует линейное невырожденное преобразование переменных

(2)

С матрицей , приводящее к нормальному виду . Рассмотрим следующее преобразование переменных:

. (3)

Если Т – матрица преобразования (3), то , а значит, (3) — линейное невырожденное преобразование переменных. Применив (3) к форме (1), получаем:

[(3)]

. (4)

Обозначим и положим

(5)

Очевидно, (5) – линейное преобразование переменных с матрицей

Так как , то (5) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (4) в квадратичную форму

. (6)

Применяя к форме (1) композицию преобразований (3) и (5), получаем квадратичную форму (6), и, таким образом, (6) эквивалентна исходной квадратичной форме (1).

Обозначим матрицу формы (6). Так как при линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака, и т. к. detA=, то

Поэтому квадратичная форма (6) положительно определена согласно теореме § 4, а значит, положительно определена и исходная квадратичная форма

Доказательство для отрицательной определенности. Обозначим , — матрицу квадратичной формы , — главные миноры матрицы . Тогда:

{K отрицательно определена}{ положительно определена}

◄

Замечание. Можно доказать, что, если хотя бы один минор четного порядка матрицы квадратичной формы есть число отрицательное, то эта квадратичная форма знаконеопределена.

Определение. Симметричная билинейная форма называется Положительно определенной, если положительно определена соответствующая ей квадратичная форма.

Упражнение. Сформулируйте критерий знакоопределенности для симметричной билинейной формы.

Источник

4.4. Преобразование матрицы билинейной формы при изменении базиса

4.5. Квадратичные формы

4.6. Методы приведения квадратичной формы к каноническому виду

Альтернативное определение[править | править код]

Связанные определения[править | править код]

Свойства[править | править код]

Преобразование матрицы билинейной формы при замене базиса[править | править код]

Связь с тензорными произведениями и функтором Hom[править | править код]

См. также[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти просмотр видео порно

Как найти попутчиков в интернете

Как найти телефон если нет интернета андроид

Добавить комментарий Отменить ответ